聚焦关键能力 融合创新意识
⦿江苏省徐州市铜山区茅村高中 徐元珍
1 引言
新情境试题是高考数学考查的热点内容之一,试题多以图、表、文并用的方式呈现,与相关生活实际加以融合,各种题型都有可能出现,考查的知识点各式各样,涉及高中数学中的所有可能知识点,准确聚焦数学的关键能力,能很好地考查学生解决简单应用问题的能力,以及考查关键能力、创新能力与创新意识.
2 与“五育”结合
与“五育”(德智体美劳)结合,巧妙把德育、智育、体育、美育、劳育等方面的知识与数学知识相结合,充分体现数学教育作为坚持“一核”(立德树人)引领,倡导“五育”并举的根本目标.
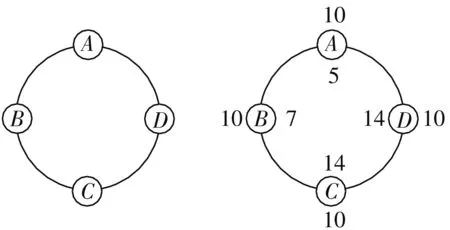
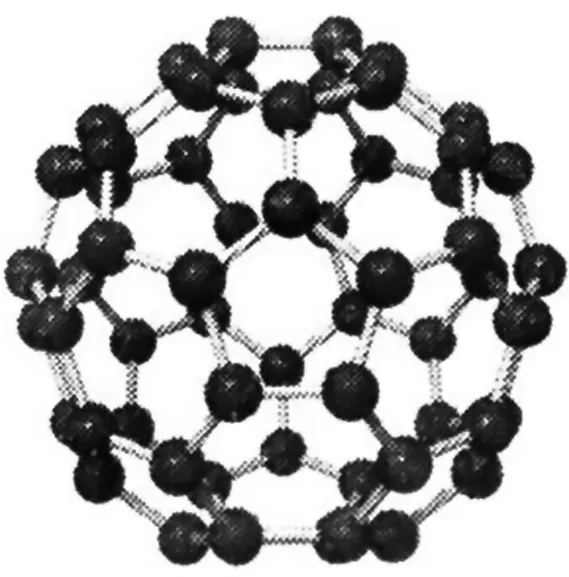
例1(2020年高考数学全国卷Ⅱ文科第3题)如图1,将钢琴上的12个键依次记为a1,a2,……,a12.设1≤i 图1 A.5B.8C.10D.15 分析:利用钢琴中的特定名称,以美育为背景设置创新问题.结合创新定义、不等关系与代数关系式,罗列出对应的参数值,确定对应参数值的组数并求和. 解析:根据关系式k-j=3且j-i=4,罗列出原位大三和弦有以下情况:i=1,j=5,k=8;i=2,j=6,k=9;i=3,j=7,k=10;i=4,j=8,k=11;i=5,j=9,k=12.共5个. 根据关系式k-j=4且j-i=3,罗列出原位小三和弦有以下情况:i=1,j=4,k=8;i=2,j=5,k=9;i=3,j=6,k=10;i=4,j=7,k=11;i=5,j=8,k=12.共5个. 综上,5+5=10.故选:C. 与社会热点结合,巧妙把发生在身边的社会热点问题与数学知识相结合,引领考生关注生活、关注社会、关注时政等,充分体现数学教育的现实生活应用以及数学服务于实际生活的目的,数学来源于生活,又服务于生活. 例2新冠病毒在世界的肆虐引起了大家对病毒的关注.假设在无干预的情况下,1名感染者一天会传染2到3名未感染者.已知甲地原有1名感染者,则在无干预情况下,3天后感染者的数量x的最大值与最小值分别是______、______. 分析:根据题设条件,分别计算感染者每人每天传染2人、3人时,3天后的感染人数,即可求出结果. 解析:假设感染者每人每天传染2人,则1天后新增感染者2人,2天后新增感染者3×2=6(人),3天后新增感染者9×2=18(人).总感染人数为1+2+6+18=27,为最少感染人数. 假设感染者每人每天传染3人,则1天后新增感染者3人,2天后新增感染者4×3=12(人),3天后新增感染者16×3=48(人).总感染人数为1+3+12+48=64,为最多感染人数. 所以3天后感染者的数量x的最大值与最小值分别是64,27,故填答案:64,27. 与生产、生活实际结合,巧妙把社会生产、现实生活实际中的相关方面与数学知识相结合,充分体现数学离不开社会生产、现实生活实际,又高于社会生产、现实生活实际,体现数学教育的应用性、生活性、实践性等. 例3某快递公司在某市有四个形状分布如图2所示的快递点A,B,C,D,每个快递点均已配备快递车10辆.根据大数据分析,为了优化效益,快递点A,B,C,D的快递车辆分别调整为5,7,14,14辆,要求调整只能在相邻的两个快递点间进行,且每次只能调整1辆,则( ). 图2 图3 A.最少需要调整8次,有1种可行方案 B.最少需要调整8次,有2种可行方案 C.最少需要调整9次,有1种可行方案 D.最少需要调整9次,有2种可行方案 分析:认真阅读题意,结合图形直观分析,通过快递点A→快递点D调整加以分类讨论,利用简单的合情推理来分析与处理. 解析:结合图形3,分析如下, 方案1:快递点A→快递点D调5辆,快递点D→快递点C调1辆,快递点B→快递点C调3辆.共调整:5+1+3=9(次); 方案2:快递点A→快递点D调4辆,快递点A→快递点B调1辆,快递点B→快递点C调4辆.共调整:4+1+4=9(次). 故选:D. 与科学技术结合,巧妙把科学技术中的相关应用与数学知识相结合,充分体现数学作为一门基础学科的重要地位,有效服务于科学技术的发展与应用,体现创新性与应用性. 例4假定一个机器人每一秒可以前进或后退一步.将该机器人放在数轴的原点,在数轴上面向正方向移动(1步的距离为1个单位长度),按照“先前进3步,再后退2步”的规律进行移动.设P(n)表示第n秒机器人所在的点对应的实数值,规定P(0)=0,则下列选项中的结论错误的是( ). A.P(3)=3B.P(5)=1 C.P(2 021)>P(2 020)D.P(2 019) 分析:根据机器人“先前进3步,再后退2步”的移动规律,发现每5秒完成一个循环,解出一个循环内对应的数值,类推相关的规律,进而分别求值再加以判断. 解析:由题意可知P(0)=0,P(1)=1,P(2)=2,P(3)=3,P(4)=2,P(5)=1,…… 以此类推得P(5k)=k,P(5k+1)=k+1,P(5k+2)=k+2,P(5k+3)=k+3,P(5k+4)=k+2.(k为正整数) 因为P(2 019)=405,P(2 020)=404,P(2 021)=405,所以 P(2 019)>P(2 020),P(2 021)>P(2 020). 因此,选项A,B,C正确,选项D错误. 故选:D. 与其他学科结合,巧妙把物理、化学、医学、天文、地理学等其他学科方面与数学知识相结合,相关数学知识、方法作为其他学科研究的思想与方法,充分体现数学教育的基础性与应用性. 例51985年,科学家发现C60分子是由60个碳原子构成的,形似足球,故名“足球烯”.如图4所示,C60分子结构稳定,其有60个顶点和若干个形状为正五边形或正六边形的面.已知C60分子的正六边形的面为20个,则其正五边形的面的个数为( ). 图4 A.10B.12C.16D.20 分析:结合C60的结构图确定其对应的每个顶点同时在3个面内,结合正五边形的顶点个数与正六边形的顶点个数之和即为60个顶点的3倍,从而建立关系式求解正五边形的面的个数. 解析:由C60的结构图知,每个顶点同时在3个面内. 设正五边形的面的个数为n,则有 5n+6×20=3×60. 故选:B. 新情境试题紧密联系生活实际,经常与“五育”结合,与社会热点结合,与生产、生活实际结合,与科学技术结合,与其他学科(化学、医学、物理等)结合,以考查学生基础知识和基本能力为主线,注重基础性、综合性和应用性,强调以素养为导向,突出考查数学建模、数据分析、逻辑推理和数学运算等核心素养,深受命题专家的青睐.
3 与社会热点结合
4 与生产、生活实际结合
5 与科学技术结合
6 与其他学科结合
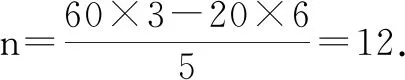
7 结论

