如何在高中数学解题中发展数学意识

⦿湖北省武汉市新洲区第三中学 商喜英

1 引言

培养数学解题能力，首先，要从基础抓起，只有这样，才能根据题目提取有效的信息，进而灵活运用已有知识去解决问题；其次，要重视培养学生猜想、分析、推理、概括的能力，只有大胆猜想加之合理的分析和推理，才能培养学生的应用意识和创新意识.可见，提升学生的解题能力有利于提升学生的综合应用能力和数学意识，然而这一能力的培养需要一个长期的过程，需要不断地渗透和磨练.

解题能力的提升一般需经过“学、讲、练、评、思”这五个阶段.第一阶段的学指“自学”.题目给出后首先让学生通过自主学习形成思路，这样在课堂上可以更有针对性地提出问题和解决问题，有利于提高听课效率.第二阶段的“讲”，主要以教师讲解为主.高中数学有一定难度，为了激发学生学习的信心，培养学生的“双基”，需要发挥教师引导、疏导和指导的作用，通过“讲”来帮助学生理解知识，建构知识.第三阶段的“练”指具有明确教学目标的典型练习.为实现知识内化、提炼解题方法、形成解题策略，需要必要的“练”.但练并非题海战术，而是通过必要的基础练习和行之有效的变式训练来提升思维的严谨性和全面性.第四阶段的“评”指教学评价.在解题中可能会产生新的思路、新的想法，也可能会产生新的错误，教学中要借助评价的激励作用和优化作用使学生在独立思考和合作探究中提升解题能力.第五阶段是“思”，即解题后引导学生进行反思.通过反思优化认知，查缺补漏，从而总结和归纳形成解题方法.相信，通过一系列的训练，学生的自学能力、分析整理能力、沟通和表达能力及合作探究能力都会有所提高.

学习的最终目的是“学以致用”，“学”为“用”的基础和前提，“用”是学好数学的动力源.在高中数学学习中，“用数学”主要体现在解题.因此，要提高学生用数学的能力，首先要培养学生的解题能力，这不单是应试的需要，更是提升学生综合能力和素养，实现学生全面发展的需要，这是数学教学的重中之重.那么如何提高呢？笔者有针对性地提出了几点认识，以期共鉴.

2 重过程，促迁移

在学习时常会遇到这样的困惑：明明听得很顺畅，为什么做的时候就无从下手或者“一做就错”呢？出现这一现象的原因是学生只是知道这个知识点“是什么”，而不能将其转化为“怎么做”.听的过程是一个静态吸收的过程，而做的过程是一个动态迁移的过程，只有“听”与“做”良性互动，才能应用所学知识解决问题.

在学习概念、公式、定理时，要在记忆的基础上加入理解和应用，若不理解或不会运用，即使背得滚瓜烂熟也不会解题.只有通过理解才能找到题目与知识间的联系，才能发现其本质和内在规律，从而运用概念、公式、定理解决问题.知识迁移是解题教学的重点，也是难点.为了突破这一教学重点和难点，在解题教学时，要引导学生关注解题的过程，在解题过程中抽象出数学思维和数学方法，进而提升知识迁移能力.

为了考查学生的知识迁移能力和数学应用能力，“新定义”成为高考的新宠.“新定义”不仅题目新颖而且内容丰富，同时兼顾公平，更能考查学生的逻辑分析和推理能力.为了让学生顺利解题，在教学中，要引导学生关注过程，形成独自思考、自主分析的能力.

例1如图1，对于大于1的自然数m的n次幂可用奇数进行“分裂”，记53的分裂中最小数为a，记52的分裂中最大数为b，则a+b=______.

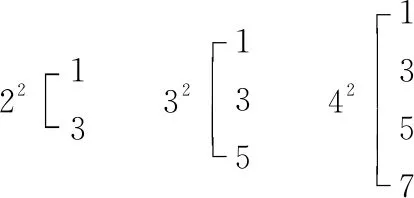
图1

分析：通过观察“分裂”找到运算规律，x2型为自上而下连续奇数，因此52分裂后为1，3，5，7，9，故b=9；x3型为从左到右的连续奇数，因此53分裂后为21，23，25，27，29，故a=21.所以a+b=30.

本题所考查的是学生的观察能力和逻辑推理能力，以及一定的自学能力.可见，数学学习靠死记硬背很难成功解决问题.因此，数学教学中要培养学生由表及里深入本质看问题的能力，同时注意数学思想和数学方法的培养，促进迁移能力和解题能力的提升.

3 轻数量，重效益

传统教学习惯于机械地强化训练，以求通过量的积累实现质的飞跃.然而高中教学时间紧，课堂时间更显宝贵.过多地练习不仅使学生容易产生厌烦心理，造成思维疲劳，课堂效率反而会降低.为此，课前教师要精挑细选，选题时要结合学情，关注知识的覆盖面，所选题目需要传递数学方法和数学思想.课上避免“满堂灌”的教学模式，尽量少讲，放权给学生，引导学生学会独立思考和合作交流.同时教学中要给学生时间表述自己的想法，加入了情感和思想的解题方法让学生印象自然更深刻，优于灌输的解题技巧和解题方法，这样更有利于学生认知的完善和自学能力的提升.课下让学生精练多思，但过多的强化训练势必占用反思、总结的时间，这样反思时间的减少会影响解题方法的形成，不利于学生进行查缺补漏.

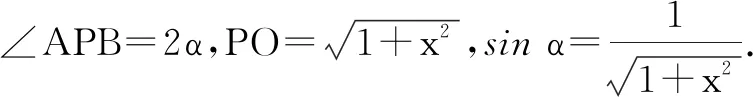
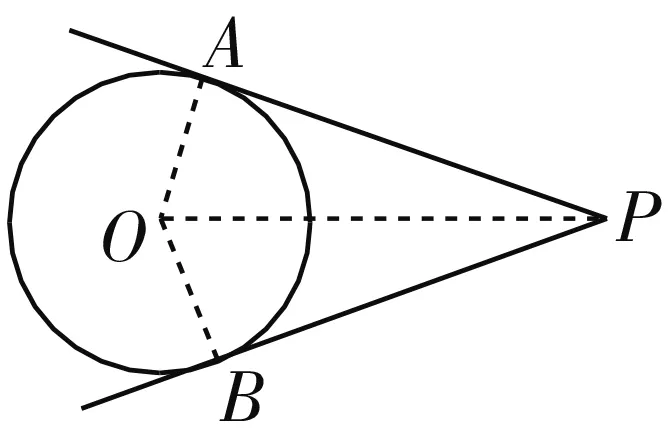
图2

向量既有形的特征，又有数的运算，是数形的完美结合.本题将向量、几何、代数运算完美地结合，实现了知识体系的建构与迁移.

4 关注错误，完善认知

学习中只有充分地认识错误，解读错误，才能找到真正的错因进而有效地查缺补漏，这是解题教学的宝贵财富，有利于学生认知系统的建构和完善.

例3现有甲、乙、丙3项任务，完成甲任务需要2人，完成乙任务需要1人，完成丙任务需要1人，现从10人中任选4人完成这3项任务，则有多少种不同的选法？

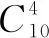
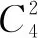
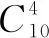
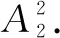
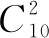
5 以学生为主体，促发展

实施高效课堂，提高学生的解题能力就要以学生的发展为根本，鼓励学生通过自主思考、主动探究来表达自己的独特想法和见解，以此促进个体发展.同时，通过教师的引导和评价来激发学生的潜能，通过学生自主合作与交流来激发自身的内在动力，有利于提升解题能力和学习效率.

6 结语

总之，学生解题能力的提升和数学意识的培养是复杂的、系统的、长期的过程，教学中要结合学生学情采用行之有效的教学手段，切勿盲目强化训练挫伤学习兴趣和创新意识.