在激发和活化学生思维中提升数学素养

⦿江苏省金湖中学 陈万斌

1 引言

学生是数学学习的主人.在学习过程中，教师要引导学生认真观察，独立思考，合作交流；引导学生亲自去发现问题，解决问题，掌握方法.在数学活动中，解题思路的探究过程是最基本的活动形式，数学问题的解决过程是学生提升核心素养的重要过程，也是通过运用数学思想加深认识和理解方法的过程.高中数学教师课堂上经常采用“一题多解”“一题多变”拓宽学生的思路；也经常通过“多题一法”帮助学生总结规律、提炼方法，深化方法的内涵即数学本质；又经常引导学生展开联想，即“方法迁移”，挖掘习题的内在关系，进行转化，达到不同方法之间的融会贯通.这些教学手段都会激发学生展开思考、拓宽思维的宽度，延长思维的深度，增强思维的张度，进而提升学生的数学核心素养.就相关的解题教学笔者做了几点思考，举例如下.

2 注重思维发散

注重思维发散常采用“一题多解”的办法.所谓培养学生的思维发散能力，就是引导学生养成多向思考的习惯，善于分析习题的条件和结论，从不同角度思考问题，寻找突破口，起到“一题顶十题”的作用，达到事半功倍的效果，有利于提升思维的广度，促进数学核心素养自然而然地渗透.

例1已知：x,y∈R,4x2+y2+xy=1，求2x+y的最大值.

解析：可设x>0,y>0,，m=(2x+y)2.

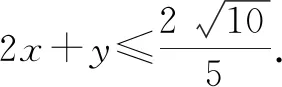
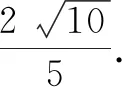
法二：(配凑法)

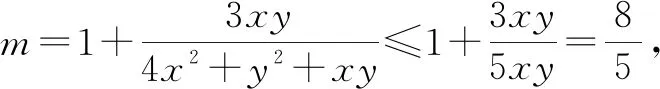
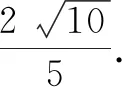
法三：(基本不等式法)

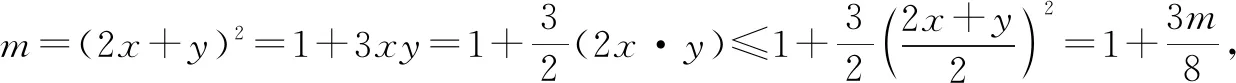
法四：(三角代换法)

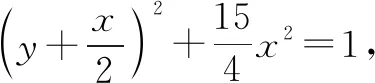
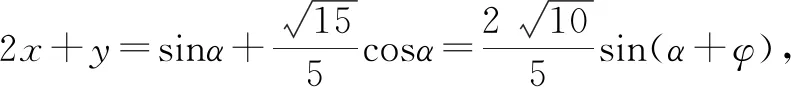
法五:(构造图形法)

构造三角形ABC，1=4x2+y2+xy,由余弦定理可设△ABC，其中

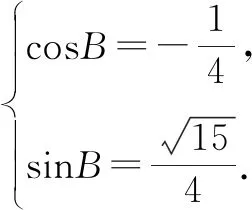
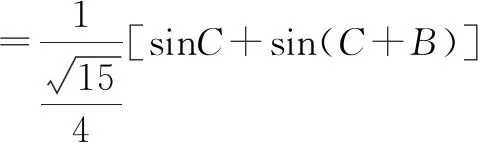
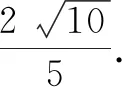
法六：(方程法)

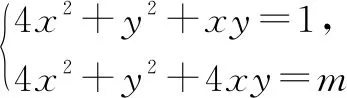
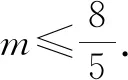
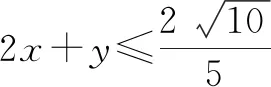
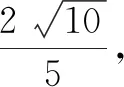
3 注重思维聚焦

注重思维聚焦常采用“多题一法”的办法.教师经常会花费较多时间和精力引导学生探究“一个典型问题”的解法，不断感悟、提升，使得一种典型的解题方法了然于胸.同时指导学生对所做习题进行总结、归纳，悟出“规律”，达到“题变法不变”的效果，即很多问题看似形式、题意、表达不同，实质是一种解答方法，这种教学会帮助学生看透问题的实质、掌握数学的本质，极大地提高思维深度，数学核心素养就会内化于心.

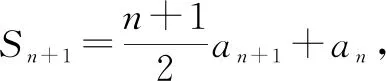
(1)求a3,a4的值;

(2)求证：数列{an}为等差数列.

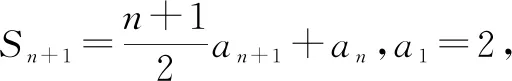
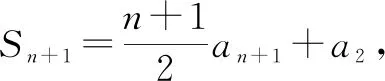
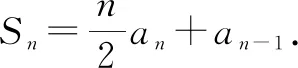
所以，n≥2时，(n-1)an+1-(n-2)an-2an-1=0.

于是nan+2-(n-1)an+1-2an=0.

再作差，得

n(an+2-2an+1+an)+2(an+1-2an+an-1)=0,

所以an+1-2an+an-1=0,数列{an}为等差数列.

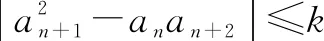
解析：因为b1+b2+……+bn=bn+2-3，

①

所以，n≥2时，b1+b2+……+bn-1=bn+1-3.

②

由式①-②，得bn=bn+2-bn+1.

于是，n≥2时，a1+a2+……+an=an+2，

③

则当n≥3时，a1+a2+……+an-1=an+1.

④

式③-④，得an=an+2-an+1.

即当n≥3时，an+2=an+an+1.

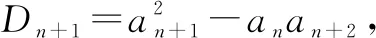
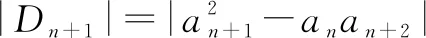
=|Dn|=……

所以k≥5,实数k的最小值为5.

4 注重思维迁移

注重思维迁移是高中学生有了一定的解题本领后，教师常会引导学生多元化思考，注意方法的结合，启发学生对不同的解题思路、办法进行比较，比较思路及思维过程的优劣、计算的繁简；启发学生优化计算、优化思维.

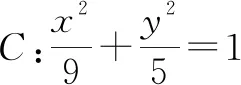
解析：设点的坐标运算比较复杂，如采用向量公式则运算比较简单.

所以

5 结语

思维是学习数学的核心，素养是研究数学的方向.在解题教学过程中，教师应多采用“一题多解”“多题一法”“方法迁移”等教学手段，引导学生揭示数学问题的内在本质，增强联想能力与创新精神，提升思维的发散、聚焦、迁移等能力.数学教学追求的效果就是随着问题的解决、方法的掌握、思想的领会、思维的强化，数学核心素养一定会快速提升.