新高考背景下的二轮数学复习建议与策略

⦿江苏省苏州市第四中学校 薛荣明

1 引言

新高考背景下的高三数学二轮复习，是新高考中一个全新且至关重要的课题，是在高三数学一轮复习中系统回顾与梳理数学基础知识、基本思想方法和基本技能这“三基”后进行综合复习的一个重要环节.本研究结合新高考背景下的高三数学二轮复习中研究考纲、考题、课本、考卷等几个重要环节，抓基础题、经典题、课本题、易错题等，剖析复习建议与对应策略，以期抛砖引玉.

2 研考纲——找准方向用力，抓基础题

认真研读高考数学考试大纲，依托考纲，明确考点，从而找准高三二轮复习的用力方向，从基础题抓起，系统全面掌握各考纲对应的考点要求.例如，对于考点：理解等比数列的概念，掌握等比数列的通项公式与前n项和公式.针对这个考点，要学生利用等比数列的定义加以应用与证明，并在此基础上熟练掌握等比数列的通项公式和前n项和公式的应用.

例1(2021年普通高等学校招生全国统一考试模拟演练(八省联考)数学·17)已知各项都为正数的数列{an}满足an+2=2an+1+3an.

(1)证明：数列{an+an+1}为等比数列；

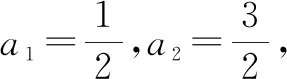
分析：第(1)问证明等比数列比较容易，借助二阶线性数列递推关系式与所要证明数列之间的关系，对递推关系加以合理变形与转化，即可得以有效证明；而第(2)问求解数列的通项公式，可以合理借助第(1)问的结果，结合数列递推关系式的变形，利用常见的破解方法与技巧，加以合理迭代处理等，能有效破解相关问题.

解析：(1)由an+2=2an+1+3an，可得an+2+an+1=3an+1+3an=3(an+1+an)，因为数列{an}的各项都为正数，则有a1+a2>0，所以数列{an+an+1}是公比为3的等比数列；

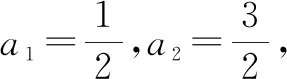
策略建议：针对等比数列这个相应的考点，新高考背景下的高三数学二轮复习中，要重视等比数列概念的理解和应用.

3 研课本——立足基础强化，抓课本题

高三数学二轮复习必须回归数学教材，借助课本的研究，从更高层次上重新全面体系化地梳理知识、思想和方法，促进数学知识结构的概括、重组与提升，诠释内在联系与规律，构建一个条理化、有序化、网络化的高效的认知体系结构，达到基础知识的强化与提升，实现数学知识间的互联互通，融会贯通，举一反三.

例2斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线交于A，B两点，求线段AB的长.

分析：此题来自普通高中课程标准实验教科书《数学·选修2-1(A版)》(人民教育出版社，2007年2月第2版)第69页例4.其与以下的高考真题几乎完全一样.

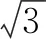
两者之间的差别就是题目中焦点弦的斜率不一样，题型不一样(一个是填空题，一个是解答题)，其他都完全一样.

策略建议：在高三数学二轮复习中，要充分以高中数学教材为蓝本，以本为本，吃准吃透.从课本题入手，合理切入，迅速进行有效的检索、判断、辨析、提取、组建，进而高瞻远瞩地选择高效、简捷的思路和方法来分析与破解.

4 研考题——选定目标突破，抓经典题

历年高考数学真题已然成为一个最好的“题源库”“母题库”，是高三数学二轮复习中的经典题源.历年的高考中，高考命题都充分体现出数学教材的示范与引领功能，源于教材意料之外，植于教材情理之中，高于教材能力之上.高考数学命题的背景、知识、方法、技巧与策略等都能在高中数学教材中追根溯源，寻觅其前世今生，源于教材往往又高于教材，体现传承与发展.

中国在维和行动中的领导决策能力尚未得到有效体现。在当今世界，国际规则往往由一些发达国家制定，在国际安全领域的联合国维和行动也不例外，很多情况下，维和人员派遣国无法充分参与维和行动各阶段的所有工作。一些国家（其中大部分为发展中国家）提供了大部分维和人员，却很少有机会参与维和决策，他们提供的一些有价值的意见也很少被采纳。中国作为参与国，因受种种因素的限制，在维和行动中很难起到主导作用。

例3(2004年高考数学全国卷Ⅱ文科第9题)已知向量a，b满足|a|=1，|b|=2，|a-b|=2，则|a+b|=( ).

分析：该高考真题与下面的2020年高考数学全国卷Ⅰ理科第14题有雷同之处：

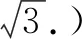
以上两个问题都可以利用平面向量的数量积公式或坐标法来处理，也可以借助“平行四边形对角线平方和定理”来处理.

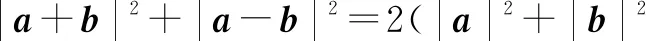
5 研考卷——针对问题点拨，抓易错题

在高三数学二轮复习中，借助一些最新的模拟考卷，从数学知识、思想方法和技能等角度加以有针对性地点拨与提升，在理解与掌握的基础上，主要剖析学生中比较常见的易错题，合理纠错，全面提升.

例4(2021年普通高等学校招生全国统一考试模拟演练(八省联考)数学·14)若正方形一条对角线所在直线的斜率为2，则该正方形的两条邻边所在直线的斜率分别为______，______.

分析：2021年1月23日，由国家教育部命题考试中心统一命题，江苏、河北、辽宁、福建、湖北、湖南、广东和重庆等八个省、市全体高三学生(参考总人数是331万多人，占了当年全国高考人数1071万人的三分之一，堪称史上规模最大的联考)参加的八省模拟演练的数学学科试卷正式出炉.该试卷对高三数学二轮复习有很大的指导意义.

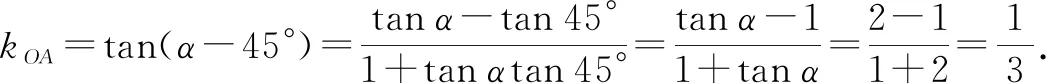
图1

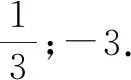
策略建议：合理借助2021年八省联考等一些重要考卷，针对性抓易错题，合理点拨，聚焦核心素养的养成，从容应对高考的变化.

6 结语

新高考背景下的高三数学二轮复习，是全面开展的专题性、针对性、能力性、技巧性、系统性复习，合理有效完善知识、总结规律、提升能力、适应高考等.因此，行之有效的新高考背景下的高三数学二轮复习，能全面有效提高短暂的二轮复习效率，避免走弯路，提升解题技巧，真正形成解题能力，养成良好思维品质，培养数学核心素养.