例谈圆锥曲线中存在性问题的解法

⦿西华师范大学 潘小琴 冯长焕

1 问题提出

圆锥曲线作为高考的必考内容，题型丰富多变.从近几年的高考试题中可看出，该类题型在考查圆锥曲线基础知识的同时，对学生的逻辑推理能力和数学运算能力也有了更加明确的要求，其中存在性问题正是圆锥曲线的经典考试题型之一.作为一种开放式的数学问题，通过这类题目的专题讲解，有助于培养学生的数学核心素养.但在实际的测试中，由于时间的限制和知识的掌握不足，导致学生在这类题目中表现出“看似套路满满，实则内容空洞”的局面.笔者曾咨询过不少学生，大多认为圆锥曲线的题目难以看懂，或者是对题目所给出的条件难以有效转化，或是计算量过大，故而产生放弃这类题目的想法，由此造成学生看不懂、不想算、得分率低或者不得分的普遍现状.本研究基于圆锥曲线存在性问题的特征和学生在此类题目中存在的疑难，以例题为依托，探究圆锥曲线中存在性问题的解法，并在强化通性通法的同时，试图寻求圆锥曲线存在性问题的最佳解题策略.

2 圆锥曲线中存在性问题的类型及对策

通过对高考试题及模拟题的分析发现，圆锥曲线中常见的存在性问题有四类：存在点问题、存在直线问题、存在参数问题、存在图形问题.但是无论哪类问题，均可通过特定元素(点、直线、参数、图形)的存在情况来说明试题的结论成立与否.

2.1 存在性问题的解题策略

2.1.1 假设结论验条件

根据题目的询问方式，一般先假设这样的元素存在使得题目的结论成立，结合假设和已知条件进行合理转化和推理论证，若根据所列出的代数式能够求解出假设的元素，则假设成立；若无法求解出这样的元素，则说明假设与题干矛盾，则不存在这样的元素.这种解题方法是解决存在性问题的通用方法，根据现有的解题经验，这种做法会涉及到圆锥曲线的基本知识、向量知识、方程思想、不等式知识等综合性知识，虽然运算过程繁杂，却也不失为一种稳妥的求解策略.

2.1.2 大胆猜测证结论

所谓大胆猜测证结论，即在解题的过程中率先说明这类元素具体的值(点的坐标、直线的方程、参数的具体数值、图形的具体形状)，再给出具体的论证推理过程.但这种方法对学生个人的运算能力和知识的掌握程度要求都非常高，故而在具体的解题过程中较少采用这种方法.

但无论采取哪种解题方式，都需要对题中的条件进行转化，转化方式会直接影响问题解决的难易程度，针对此种情况，笔者提出以下几种条件的转化策略.

2.2 条件转化策略

2.2.1 透彻问题本质，简化运算过程

解析几何是利用代数知识解决几何问题，但其实质依旧是几何问题，在对试题条件进行分析时，要抓住条件所反映出的几何本质，将几何条件代数化，帮助学生简化运算过程，提高运算效率.这不但要求学生对圆锥曲线的基础知识及其几何性质非常熟练，并且对知识迁移能力也有着极高的要求.因此学生在日常学习时，既要对圆锥曲线的知识进行及时梳理，也要对这些知识点的常见题型进行识别和总结，以便在存在性问题的求解过程中谋划出路.

2.2.2 选择适当参数，优化解题步骤

解析几何中涉及到的未知点的坐标和未知直线的方程过多，根据已知条件，要尽量减少未知参数的个数，加强未知参数和已知条件的联系，以期优化解题过程.例如圆锥曲线中会用到直线方程，在直线斜率存在的情况下，常采用含有斜率的直线方程(类似于y=kx+b)，根据韦达定理将未知点的坐标关联起来.但对于有些题目，例如下面的试题1，为了找出这样的点G，将直线方程设成x=my+n，在无需考虑直线的斜率存在与否的同时，既可以减少计算又可以优化解题过程.

2.2.3 根据题目条件，选择适当坐标系

解析几何题的经典做法是采用平面直角坐标系，从解题经验来看，这无疑是一种稳妥的解题工具.但解析几何知识点多而繁杂，需要设出未知点的坐标，增加参数的同时，会使得运算步骤冗长，容易在解题过程中导致学生思路混乱，解题受阻，从而导致试题完成率不高，解题失败.而极坐标系极大地减少了参数的个数，简化运算步骤，故而在有效的时间内采用极坐标法能事半功倍.但究竟选择哪种方式更为合适，与学生对知识的熟练程度和试题的特征有关.

3 例题呈现

3.1 存在点问题

试题1已知动点P在圆M:x2+y2-2x-15=0上，点N(-1,0)，点Q是线段PN的垂直平分线与线段PM的交点.

(1)求点Q的轨迹方程；

(2)设点Q的轨迹为曲线C，过点N作曲线C的两条互相垂直的弦，两条弦的中点分別为E，F，过点N作直线EF的垂线，垂足为点H，是否存在定点G，使得|GH|为定值？若存在，求出点G的坐标；若不存在，说明理由.

解析：(1)由题知，圆M的圆心M(1,0)，半径为4.因为点Q在线段PN的垂直平分线上，所以 |QP|=|QN|，|QN|+|QM|=|MP|=4>|MN|=2，所以点Q的轨迹是以M,N为焦点的椭圆.

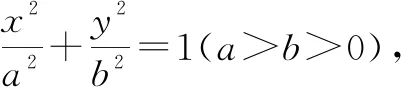
(2)假设存在这样的点G，使得|GH|为定值.

(ⅰ)当两条弦中有一直线斜率不存在时，直线EF位于x轴上，此时无法确定点G坐标.

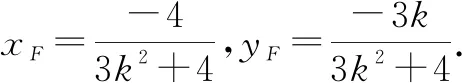
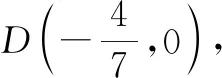
注：本题可设直线l1的方程为x=my-1(m≠0),则无需讨论斜率不存在的情况.

反思：本题中看似没有给出G点的位置信息，如果不能正确理解给出的几条直线关系，会感觉无从下手.但深究条件可知，直线EF始终过定点，且该定点位于x轴上，由此再结合直角三角形的性质，便可求得G的坐标.而在求解过程中发现，除了常见的联立方程、韦达定理身影外，找到关键的直线方程至关重要，因此对直线方程的选择，除了考虑计算量这个因素外，还要看设出的直线方程是否能够优化解题过程.

3.2 存在直线问题

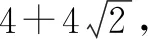
(1)求点M的轨迹E的方程；

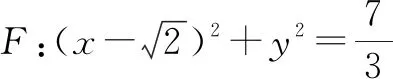
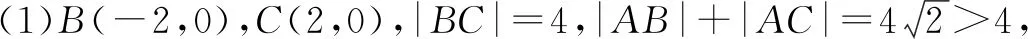
(2)(ⅰ)当直线l⊥x轴时，此时l的方程为x=0.设点P在上方，根据P，Q，R，S四点的位置可求得这四点的具体坐标，从而验证得到|PR|=|QS|，即直线l的方程能为x=0.

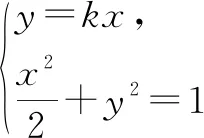
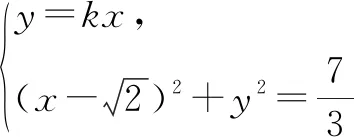
综上所述，直线方程为x=0，y=x或y=-x.

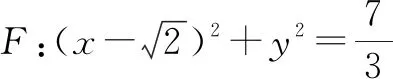
反思：纵观解题过程发现，两种解题方法有重叠的部分，但相较之下第二种解法在优化解题步骤的同时，也能在有限时间内高效解题.学生在解圆锥曲线的弦长问题时，习惯采用含有直线斜率的距离公式来转化弦长，殊不知，这种做法无形中增加了参数，计算过程复杂.此题也在提醒学生，若遇到圆与曲线结合的题型，弦长是直线与圆相交所产生的，利用圆心和圆的半径求解弦长，能够降低运算量.当然题目中涉及的动点过多时，要充分利用数形结合，在图形中大致确定动点所在位置，以便对题中条件进行合理转化.

3.3 存在参数问题

(1)求曲线C的方程；

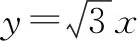
(2)假设存在这样的实数t，证明如下：

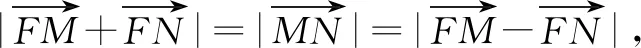
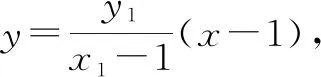
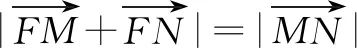
3.4 存在图形问题

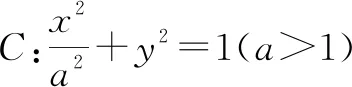
(1)求椭圆C的标准方程；

(2)以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形，这样的直角三角形是否存在？若存在，请说明有几个；若不存在，请说明理由.

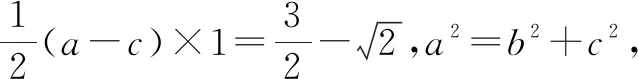
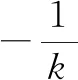
由|BM|=|BN|，得

故根据对称性可知，存在这样的内接等腰直角三角形，且有三个.

4 解题反思

值得我们思考的问题是，无论是哪一类型的存在性问题，即便是选择简化的解题方法，仍需要“精通熟练”掌握圆锥曲线的知识.知己知彼方能百战百胜.在上述例题的呈现中我们发现，最佳解法的选择并不是一开始就形成的，而是在不断尝试中产生.条件的识别与合理转化至关重要，这就要求学生在学习中不断积累.圆锥曲线涉及到的未知参数较多，计算问题也是学生的一大难点，许多学生被这“庞大而复杂”的计算量阻挡在了试题门外，望而却步.对存在性问题，我们需要做的是，理清存在性问题的关键步骤和核心解法，在大胆假设中寻求问题的答案，在反思质疑中形成问题的完善解法，在论证推理中提升自己的思维水平，在动手操作的过程中培养自己的数学运算能力.