用于光纤干涉传感器的高稳定PGC 解调技术

肖文哲，程 静，张大伟*，孔 勇，叶华龙，何 军

1 上海理工大学光电信息与计算机工程学院，上海 200093；2 复旦大学材料科学系，上海 200433；3 上海工程技术大学电子与电气工程学院，上海 201620

1 引言

分布式光纤干涉传感器作为当前光纤传感技术中最有竞争力的技术之一，具有抗电磁干扰、抗腐蚀、损耗低、灵敏度高、体积小和定位精确等优势。光纤干涉传感器已经引起了一些研究者的广泛关注[1-4]。传感器可以将外部干扰转换为沿传感光纤的光相位变化，通过光电探测器将接收到的光信号转换为电信号，然后通过解调算法解调相位变化以获得外界干扰[5-7]。光纤干涉传感器可用于温度、应力以及外界长距离扰动信号的检测[8-9]。目前，光纤分布式传感器已广泛应用于生活中的许多领域，包括周界安全、地震波检测、入侵检测、铁路安全监控以及其他重要领域[10-16]。

已经提出了许多解调方法应用在分布式光纤干涉传感器中，常用的包括3×3 耦合器解调法[17-20]、数字相干I/Q 解调法[21-22]、相位生成载波(PGC)解调法[23-26]等。其中基于3×3 耦合器解调法不需要用调制器，具有结构简单、响应带宽高、动态范围大等优点。但由于需要多个光电探测器进行解调，增大了解调系统成本，且系统容易受外界影响[20]。数字相干I/Q 解调法是一种利用本地光与瑞利散射光本地外差产生干涉信号后进行正交解调的方法。数字相干I/Q 解调法结构简单，系统信噪比和灵敏度也较高。但其解调结果容易受到激光器频率漂移引起的相位噪声和本地光与瑞利散射光偏振态不稳定的影响，从而使解调准确性下降[21-22]。PGC 解调法具有动态范围大、灵敏度高、线性度好、信噪比高等优点，利用PGC 解调算法有利于消除相位漂移引起的干涉输出不稳定性[26]。为了解调出光纤干涉传感器由外界干扰产生的相位变化，一般采用PGC 微分交叉相乘(PGC-DCM)和PGC 反正切(PGC-Arctan)解调算法。PGC-DCM 解调方法易受光强度干扰(LID)的影响，同时对载波调制深度C也比较敏感[27]。PGC-Arctan 解调方法与PGC-DCM 解调算法相比算法结构简单从而可以降低信号处理的时间，同时PGC-Arctan 解调方法对光强干扰(LID)不敏感。但是，对于PGC-Arctan 解调结果，其反正切函数的参数包括解调相位和含有C值的贝塞尔函数。此时，C值会给解调算法引入非线性失真，当C 值偏离2.63 rad 时，系统会引入较严重的非线性失真[28]。因此，由于载波调制深度的偏离从而导致解调结果的失真是PGC-Arctan 算法的主要问题。

Yu 等[29]提出了基于Ф-OTDR (phase optical timedomain reflectometer)和相位载波解调算法的分布式光纤振动传感器，但是其解调结果受到调制深度和光强度干扰的影响，所以会给解调系统带来不稳定性。然后，他们提出PGC 单路微分相除(PGC-SDD)解调算法[30-31]，与传统的PGC-DCM 和PGC-Arctan 解调算法相比，PGC-SDD 解调方法具有较高的稳定性和较低的谐波失真，但是C值的偏离会给PGC-SDD 算法引入较严重的谐波失真。然而，在分布式光纤干涉传感器中，外界温度的变化会影响相位调制器的性能，进而影响施加到压电换能器(PZT)上的调制信号。在实际应用中，调制深度由施加到 PZT 上的调制信号的幅度、环境温度和PZT 的特性决定。因此很难将C值保持在一个稳定的值。之后，又有一些研究学者采用一些方法来计算相位调制深度来消除调制深度的影响提高系统的稳定性，但是它们解调过程太复杂[32-34]。因此，如何消除相位调制深度和光强扰动以提高系统的稳定性成为PGC 解调技术中的一个重要问题。

本文提出了一种改进的PGC 解调算法(PGC-SDDDSM)。我们引入了一种差分自乘(DSM)算法来消除基于单路微分相除PGC 解调算法(PGC-SDD)的调制深度C的影响。将解调结果不受调制深度和光强干扰影响的新型PGC 解调算法首次应用于光纤干涉传感器，有效抑制谐波干扰，提高传感系统的稳定性。本文第二部分介绍了光纤干涉传感器的工作原理和解调算法的原理，第三部分介绍了解调算法的仿真结果，第四部分阐明了实验和结果，第五部分是本文的结论。

2 理论推导

分布式光纤干涉传感器的干涉信号可表示为

其中：A为 输入光的强度，与光源强度有关；B=kA为干涉光的强度(干涉条纹可见度k≤1)，与光源强度和干涉条纹可见度有关；Ccos(ωct)为PGC 调制信号，其中C为调制深度，ωc为调制频率； φ(t)为包含扰动信息的待测信号。

然后将干涉信号I(t)进行处理，干涉信号展开可以得到：

其中：J2n+1(C) 和 J2n(C)分别是奇次贝塞尔函数和偶次贝塞尔函数。PGC-Arctan、PGC-DCM、PGC-SDD 和改进的PGC 算法的原理框图分别如图1(a)～1(d)所示。

通过两个乘法器将干涉信号I(t)分别与基本载波Gcosωct和第二谐波Hcos2ωct相乘，为了得到更好的解调结果，载波信号与干涉信号需要满足同步进行。通过两个截止频率略低于载波的低通滤波器进行滤波，滤波后的信号可以表示为

经过两个低通滤波器滤波后，信号直接相除，相除后的信号通过反正切函数进行扩展，再通过高通滤波器得到PGC-Arctan 的解调结果：

经过微分交叉相乘、相减、积分运算处理之后，再通过高通滤波器可得到PGC-DCM 算法[35]解调结果：

令G=H=1，则PGC-DCM 算法的解调结果受调制深度和光强干扰的影响。PGC-Arctan 算法的解调结果不受干涉光强干扰的影响，但是调制深度变化会导致 J1(C)/J2(C)发生变化，使得 J1(C)/J2(C)≠1，给解调系统造成影响，导致解调结果出现非线性失真。为降低谐波失真对解调结果的干扰，后来提出了一种单路径差分相除PGC 解调算法[30](PGC-SDD)，该解调算法流程图如图1(c)所示，L1(t)经过微分，可得到：

将L1′(t)与L2(t)相除然后进行积分器和高通滤波器，可以得到：

SPGC-SDD(t)=[J1(C)/J2(C)]·φ(t). (8)

从上式(8)相位解调的理论表达式中可以看出，PGC-SDD 算法能够抑制光强的影响，也能够抑制由于C值影响的非线性谐波失真，但是该解调算法仍然与调制深度C值相关。受到调制深度C值影响出现线性失真，给解调结果造成干扰。为了消除PGCSDD 算法中的C值的影响，提出了一种施加在分布式干涉传感器中的新型解调算法，其原理框架如图1(d) 所示。经过低通滤波器滤波后的信号为L1和L2，如式(3)和式(4)所示，然后分别对L1和L2进行微分运算，再将微分后的式子分别与L1和L2自身相乘，得到：

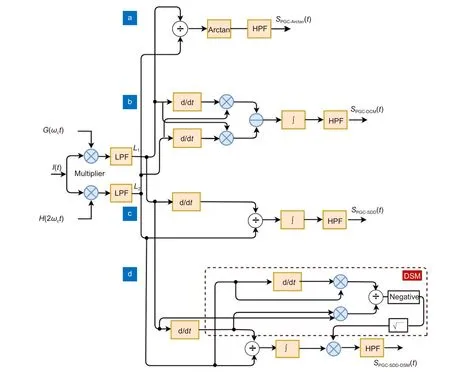
图1 PGC 解调算法结构框架图。(a) PGC-Arctan；(b) PGC-DCM；(c) PGC-SDD；(d) PGC-SDD-DSMFig.1 Schematics of the PGC demodulation algorithm.(a) PGC-Arctan;(b) PGC-DCM;(c) PGC-SDD;(d) PGC-SDD-DSM

接下来计算式(11)取负运算后的平方根：

实际应用中，相位调制深度通常在0 到3.7 rad范围内。根据贝塞尔函数性质，当0 ＜C＜3.7 rad 时，J1(C)＞0 和 J2(C)＞0。将式(8)与式(12)相乘，PGCSDD-DSM 算法的解调结果可得：

从上式可以看出，改进的PGC 解调算法对光强干扰和调制深度均不敏感，可以消除光强干扰和调制深度变化引起的谐波失真，从而大大降低解调结果的误差。表1 是上述四种PGC 算法的参数性能比较。

表1 四种算法的性能比较Table 1 Comparisons of four PGC demodulation algorithms

3 仿真与分析

为了验证提出的新型PGC-SDD-DSM 算法的有效性，进行了一系列仿真对比实验。利用改进的算法方案对传感系统进行解调，测试该方案对调制深度C值的敏感度，以及与PGC-SDD、PGC-DCM 和PGCArctan 算法的对比实验。实验中，载波信号频率为50 kHz，采样频率为4 MHz，干涉信号中直流分量和交流分量分别设置为1 V。

将频率为1 kHz，幅度为1.4 rad 的干扰信号施加在系统当中，来测试PGC-SDD-DSM 解调算法对C值的敏感程度。在调制深度C值取1.5 rad、2.0 rad、2.5 rad、3.0 rad 和3.5 rad 时，几种解调算法解调出来的仿真实验结果分别如图2(a)～2(d)所示。

如图2(a)所示，当C取不同值时，PGC-SDDDSM 算法解调结果几乎不发生变化，其幅值大小在1.4 rad 左右。如图2(b)所示，PGC-SDD 解调算法的解调结果随C值变化显著。由理论计算可知当C值取2.63 rad 时J1(C)/J2(C)=1，此时解调结果的线性误差最小。因为C值取2.5 rad 时相比C值取1.5 rad、2.0 rad、3.0 rad 和3.5 rad 而言更接近2.63 rad，此时J1(C)/J2(C)更加接近1，所以C值取2.5 rad 时在仿真实验中能达到最好的解调效果。如图2(c)所示，PGC-Arctan 解调算法解调结果对于不同的调制深度C值，解调结果变化显著。随着C值与2.63 rad 偏差越小，谐波失真越小，解调效果就越好。所以C=2.5 rad 时解调结果非线性失真最小。然而当C=3.5 rad 和C=1.5 rad 时出现严重谐波失真，此时解调结果非线性失真最大。所以调制深度C值变化会使得PGC-Arctan 算法的解调波形幅值发生变化，同时使得解调波形失真。如图2(d)所示，PGC-DCM 解调算法解调波形随C值变化显著。随着C值与2.37 rad 的偏差增加，解调出来信号幅度递减，解调信号失真越大。当C值取值为2.5 rad 时能够还原出0.98 rad 振幅的信号，此时能够解调出最大的原始信号。当C值取3.5 rad 时还原信号振幅大小为0.72 rad，此时解调出的信号与原始信号存在最大偏差。所以调制深度C值变化会使得PGC-DCM 解调算法解调波形幅值发生明显变化。由此可见，实际仿真验证与理论推导相一致。

图2 C=1.5 rad、2.0 rad、2.5 rad、3.0 rad 和3.5 rad 时不同PGC 算法解调结果。(a) PGC-SDD-DSM;(b) PGC-SDD;(c) PGC-Arctan;(d) PGC-DCMFig.2 Demodulation signals of different PGC demodulation algorithms with C=1.5 rad,2.0 rad,2.5 rad,3.0 rad and 3.5 rad.(a) PGC-SDD-DSM;(b) PGC-SDD;(c) PGC-Arctan;(d) PGC-DCM

从图2 可看出在同样干涉信号和实验条件的情况下，PGC-SDD-DSM 解调算法解调结果优于其它三种算法，且其对调制深度C值不敏感，具有较高的稳定性。

4 实验和结果分析

搭建了一套实验系统来验证所提出的 PGC 解调算法的性能，如图3 所示。在该实验系统中，传感光纤为单模光纤，信号发生器作为振动源驱使缠绕在PZT 上的光纤发生振动，从而产生振动信号。为了进行PGC 调制并获得外部干扰信号，实验系统包含两个马赫-曾德尔(Mach-Zehnder)干涉仪。其中第一个Mach-Zehnder 干涉仪的作用是评估系统在引入光强干扰条件下的稳定性，第二个Mach-Zehnder 干涉仪的作用是引入外部干扰信号和PGC 信号。波长为1550 nm 的稳定可调谐激光器用作传感器系统的光源。将频率为 50 Hz 的正弦信号施加到PZT1 上以产生干扰深度为 0.7 rad 的光强干扰 (LID) 信号。使用隔离器(ISO)降低光纤传感器中相干瑞利散射噪声，然后将频率为1 kHz 的测试信号和频率为50 kHz 的载波信号分别施加到PZT2 和PZT3。高灵敏度光电探测器(PD)将干涉光信号转换为电信号，输出信号由数据采集卡(美国NI 公司生产的DAQ，USB-6251)以1.25 MS/s 的采样率进行采样，然后通过USB 存储器传输到计算机。采用MATLAB 和Labview 软件，对提出的PGC 算法进行解调处理得到解调信号。

图3 实验系统结构图Fig.3 Schematic of experimental setup

在PZT2 处施加频率为1 kHz，信号幅度为2.0 rad的振动信号，原始振动信号波形图如图4 所示。PZT3处施加相位载波信号的频率为50 kHz，调制深度C设置为1.5 rad。

图4 原始信号Fig.4 Original signal

图5(a)～5(d)分别是PGC-DCM、PGC-Arctan、PGC-SDD 和PGC-SDD-DSM 解调算法的解调结果。实验中调制深度C主要与外加电信号的稳定性、压电陶瓷的特性以及光纤参数的变化有关。一般来说，电信号和压电陶瓷的稳定性较好，但光纤的折射率同时会受到温度、应变等因素的影响，因此调制深度C可能会出现波动。从图5(a)可以看出基于PGC-DCM 解调算法的解调结果不稳定，解调幅值受到光强的影响，使得其幅值发生不同程度的变化。其最大幅度值也与原始信号幅度值存在较大差异，这主要是由于光强干扰和调制深度C值而导致的。从图5(b)可看出PGCArctan 解调结果不受光强干扰的影响，使得其具有稳定的幅度值，但是由于调制深度C值的影响导致谐波失真，从而出现明显的非线性失真现象。在图5(c)中，PGC-SDD 的解调信号仍然不稳定，其最大幅度值接近1 rad，该算法解调结果受C值变化明显而出现线性失真现象。相比之下，从图5(d) 可以看出，PGCSDD-DSM 的解调结果与原始信号非常接近。解调结果的幅值稳定且谐波失真小。这表明提出的PGCSDD-DSM 算法稳定性高，不受调制深度和光强干扰的影响。

图5 当C=1.5 rad 时不同PGC 算法的解调时域结果。(a) PGC-DCM;(b) PGC-Arctan;(c) PGC-SDD;(d) PGC-SDD-DSMFig.5 Demodulation time domain results of different PGC algorithms when C=1.5 rad.(a) PGC-DCM;(b) PGC-Arctan;(c) PGC-SDD;(d) PGC-SDD-DSM

基于四种不同算法的解调结果的频谱图如图6 所示，其对应图5 中的四种解调结果。我们使用信纳比(SINAD) 和总谐波失真 (THD)来评估PGC 算法的解调性能。THD 定义为所有谐波的等效均方根(RMS)幅度与基频幅度之比，SINAD 定义为基频功率与所有噪声和谐波功率之和的比值。

从图6(a)可以看出，基于PGC-DCM 算法的解调结果的失真分量主要是测试信号的一阶和二阶边带，这是由光强扰动和外部环境干扰引起。与PGC-DCM解调算法相比，改进的解调算法可以抑制LID 引起的失真，并具有更高的SINAD。与PGC-Arctan 解调算法相比，改进后的解调算法可以很好地抑制谐波失真，大大降低无关信号的频率干扰。当C=1.5 rad 时，实验中使用改进解调算法产生 35.56 dB 的SINAD，相比使用 PGC-DCM、PGC-Arctan 和 PGC-SDD 算法分别可获得 10.87 dB、24.19 dB 和 6.38 dB 的增益。表2中对四种算法的解调结果进行了比较。从表2 中可看出，改进PGC 解调算法的解调结果相比其它三种解调算法而言，具有最低的THD 和最高的SINAD。

表2 四种算法的解调结果性能对比Table 2 Performance comparison of demodulation results of four algorithms

图6 当C=1.5 rad 时不同PGC 算法的解调频域结果。(a) PGC-DCM;(b) PGC-Arctan;(c) PGC-SDD;(d) PGC-SDD-DSMFig.6 Frequency spectrums of the demodulation results of different PGC algorithms when C=1.5 rad.(a) PGC-DCM;(b) PGC-Arctan;(c) PGC-SDD;(d) PGC-SDD-DSM

根据解调结果计算出THD 和SINAD，以评估改进的PGC 方法的谐波失真性能。图7 和图8 分别显示了在不同调制深度C值下，PGC-DCM、PGCArctan、PGC-SDD 和改进的PGC 解调算法测得的THD 和SINAD。

如图7 和图8 所示，当C值的范围从1.5 rad 到3.5 rad 时，对于PGC-DCM 方法，THD 范围从0.07%到0.09%，SINAD 从23 dB 到25 dB。对于PGC-SDD解调算法，其THD 值从0.035% 到 0.07%，SINAD值在25 dB 到 30 dB 范围内，由于PGC-DCM 受光强干扰的影响，相比PGC-SDD 解调算法而言具有较低的SINAD 和较高的THD。对于PGC-Arctan 解调算法，其解调结果的THD 值在C=2.63 rad 左右时达到最低值0.08%，C值越偏离2.63 rad,THD 值就越大，最大可达0.7%。同样地，SINAD 在C=2.63 rad 左右时达到最大值35 dB，C值越偏离2.63 rad，则SINAD值就越小，最小值为11 dB。这主要是因为在C=2.63 rad时， J1(C)/J2(C)=1，此时PGC-Arctan 解调结果几乎不受调制深度C值影响，从而可以消除解调结果中由于调制深度而导致的非线性谐波失真，使得其在C=2.63 rad 时具有最优的解调性能。这表明对于PGCArctan 解调算法而言，C值为2.63 rad 左右时可取得最低的THD 值和最高的SINAD 值，PGC-Arctan 解调算法随C值偏离2.63 rad而出现不同程度的非线性谐波失真，使得其解调结果偏离最低THD 值和最高的SINAD 值。然而，对于PGC-SDD-DSM 解调方法，该解调算法不受调制深度和光强的干扰，其解调结果的THD 从0.02%变为0.05%，SINAD 从35 dB 变为37 dB，这表明了PGC-SDD-DSM 解调方法几乎不随调制深度C值变化而变化。与PGC-DCM、PGC-SDD和PGC-Arctan 解调方案相比，PGC-SDD-DSM 解调方案在1.5 rad 至3.5 rad 的C值范围内实现了低于0.1%的低THD 和高于35 dB 的高SINAD。这些均表明PGCSDD-DSM 方法的高稳定性能。实验中改进PGC 解调算法随C值变化而产生THD 值和SINAD 值的小范围波动现象，这主要是因为光纤传感器随外界环境变化而导致其解调信号发生改变，进而影响到解调信号的THD 值和SINAD 值。

图7 对不同的调制深度C 值对应的THDFig.7 THD of the proposed PGC algorithm with modulation depth C

图8 对不同的调制深度C 值对应的SINADFig.8 SINAD of the proposed PGC algorithm with modulation depth C

信号发生器用于在PZT2 处产生50 Hz 的正弦调幅信号，以验证同一频率下不同幅度信号的解调精度和幅度响应。我们将理论值与实际值进行比较。振动信号的原始实际信号(蓝色曲线)和解调信号(红色曲线)的时域波形如图9 所示。结果可看出，所提出的解调系统具有较高的幅度解调精度和良好的线性幅度响应。

图9 解调波形(红色)和原始波形(蓝色)Fig.9 Demodulated signal waveform (red) and original signal (blue)

接下来，为了进一步验证光纤干涉仪解调系统中相同幅度的不同频率信号的解调精度和频响特性。信号发生器生成幅度为 1.0 V、频率范围为 80 Hz 至 280 Hz的扫描信号。该信号也作用于 PZT2，然后使用所提出的PGC-SDD-DSM 解调算法解调出施加在PZT2 处的变频信号。实际信号(蓝色曲线)和解调信号(绿色曲线)时域信号如图10 所示。实验结果表明，信号波形恢复效果较好。同时，图中的时域信号清楚地表明，当振动信号的幅度恒定时，所提出的解调系统具有良好的频率响应。

图10 解调波形(绿色)和原始波形(蓝色)Fig.10 Demodulated signal waveform (green) and original signal (blue)

动态范围定义为在没有明显失真情况下的最大可探测信号幅度和最小可探测信号幅度的功率比值。经过PGC 解调之后的传感系统的背景噪声可视为最小可探测信号幅度。本实验系统中使用PGC-SDD-DSM解调技术的背景噪声接近-33 dB，基于PGC-SDDDSM 解调系统的动态范围随着测试信号频率的增加而减小，如图11 所示。当测试信号频率为100 Hz 时的动态范围为88.29 dB，测试号频率为1 kHz 时的动态范围为57.63 dB。

图11 基于PGC-SDD-DSM 算法解调系统的动态范围Fig.11 Dynamic range of the demodulation system based on the PGC-SDD-DSM algorithm

5 结论

本文介绍并实验证明了一种对调制深度C和光强干扰LID 均不敏感的新型PGC-SDD-DSM 解调算法。这种PGC-SDD-DSM 解调算法稳定性高、谐波失真小。理论仿真结果表明，与PGC-SDD、PGC-DCM和PGC-Arctan 算法相比，所提出的解调算法对相位调制深度不敏感。对于不同的调制深度C值，改进PGC 算法的解调信号幅度值几乎不发生变化。首次将PGC-SDD-DSM 算法应用于光纤干涉传感器中。实验结果表明，PGC-SDD-DSM 算法可以同时抑制由于光强干扰和调制深度引起的谐波失真。该算法能够准确解调出原始信号，具有较高的稳定性。当C值为1.5 rad 时，实验系统中使用所提出PGC 解调算法解调结果的SINAD 为 35.56 dB，与使用 PGC-DCM、PGC-Arctan 和 PGC-SDD 算法相比分别可获得 10.87 dB、24.19 dB 和 6.38 dB 的增益。此外，使用改进后的PGC 解调算法还可以解调具有更好幅度响应和频率响应的非周期信号。随着PGC-SDD-DSM 解调技术的引入，可以显著提高光纤干涉传感器的性能。