旋磁光子晶体元件的高效数值模拟
王雄辉,胡 真
(河海大学 理学院, 南京 211100)
光子晶体[1]是由介电常数不同的介质在空间中按周期排列制成的新型人造周期性材料,它以光的波长尺度为周期,其最重要的性质是具有光子带隙。频率落在带隙内的光不能在光子晶体内传播,因此光子晶体具有独特的控制光的能力。光子晶体波导管是通过在完整的光子晶体中引入线缺陷破坏其内部周期性结构形成的,频率落在光子带隙内的光可以在线缺陷波导管中传播,在远离线缺陷时会迅速衰减,因此线缺陷起到导波的效果。光子晶体波导管是连接集成光路各元件之间的桥梁,是光信号传输的主要载体。利用光子晶体和光子晶体波导管可以制造各种光学元件,如高性能发光二极管[2]、超低功率激光器[3]、光子晶体谐振腔[4]、超高Q滤光器[5]等元件,这些元件具有集成度高、性能优异等优点,在大规模集成光路和全光网络中具有广阔的应用前景。
近年来,由旋磁各向异性材料制成的旋磁光子晶体得到了广泛关注,其中的旋磁各向异性材料是指材料在各个方向上具有不同的磁导率。旋磁光子晶体在外加磁场的作用下打破了时间反演对称性,获得了各向同性光子晶体所不具有的可控性,比如通过在旋磁光子晶体中引入线缺陷形成旋磁光子晶体波导管,波导管中的光波在外加磁场的作用下可以实现单向传输。利用旋磁光子晶体和旋磁光子晶体波导管可以制造出一系列可控光学元件。例如,Nazari[6]在2016年制造了一种可单向传输的超紧凑型光隔离器;Esmaieli等[7]在2011年制造了一种μ可切换的紧凑型对称功率分配器;Zhang等[8]在2013年制造了一种具有沿特定端口定向传输的四端口旋磁光子晶体环形器;吴昌义[9]在2016年设计制造了具有高对比度、大带宽、小尺寸的光子晶体磁控二选一光路选通开关。这些旋磁光子晶体元件具有高透射率、大带宽、小尺寸、可控、高消光比和低插入损耗等优势,在光通信和光信号处理等领域中扮演着重要角色。
在模拟和分析旋磁光子晶体元件的过程中,有效的数值方法非常重要。目前已有的数值方法存在各种局限性。例如,时间域下模拟的时域有限差分方法[10]对传输和反射光谱这类在频率域下更容易模拟的问题,使用时并不方便。标准频域下模拟的数值方法包括有限元法[11]、平面波展开法[12]、传输矩阵法[13]等,其中有限元法和平面波展开法需要离散晶格内部,建立边值问题涉及的线性方程组规模大、未知数多且计算量大;传输矩阵法存在数值不稳定的缺陷。近年来,Huang等[14]提出了能有效模拟光子晶体的Dirichlet-to-Neumann(DtN)映射方法,Yuan等[15-16]利用DtN映射方法计算二维光子晶体带隙;Ye等[17]利用DtN映射方法计算二维三角形排列和蜂巢状排列光子晶体的等频线;Wang等[18]利用DtN映射方法计算二维蜂巢状排列光子晶体波导;Hu等[19]利用DtN映射方法计算二维各向同性光子晶体元件的传输和反射光谱,分析了有损周期介质结构中连续谱附近具有复频率的束缚态[20-21]。单元晶格的DtN映射将单元晶格边界上的波动场映射成边界上的法向导数,避免在单元晶格内部进行离散,减少了计算量。对于相同的单元晶格,只需要构造一次DtN映射。旋磁光子晶体元件有大量相同的单元晶格,故在计算旋磁光子晶体元件过程中有很大优势。
本研究扩展了DtN映射方法,将其用于计算二维旋磁光子晶体元件的传输和反射光谱。方法步骤为:① 计算结构中所有不同类型单元晶格的DtN映射,单元晶格的DtN映射可以用一个小矩阵近似表出;② 利用计算出的单元晶格的DtN映射构造出超级晶格的DtN映射,在超级晶格的边界上建立特征值问题,求解出波导管内的Bloch模;③ 基于求解出的Bloch模建立边界条件截断光子晶体波导管,截取有限的计算域;④ 在截取的计算域中所有单元晶格的每条边上建立一个线性方程,最终得到一个包含所有边上波动场的线性方程组。为了建立线性方程组,可分别在计算域的内部和边界上建立线性方程。由于计算域内部的每条边都位于2个相邻单元晶格的交界面上,故利用2个单元晶格的DtN映射和这条边上波动场法向导数的连续性建立线性方程。对于计算域边界上的边,利用单元晶格的DtN映射、截断波导管的边界条件和这条边上波动场法向导数的连续性建立线性方程。
1 控制方程
研究对象为由无限长且平行的介质柱按正方形周期排列组成的二维旋磁光子晶体元件。如图1所示,二维旋磁光子晶体环形器即二维旋磁光子晶体元件中的一种,由Zhang等[8]提出。图1中红色部分表示旋磁光子晶体,蓝色部分表示各向同性光子晶体,其中L是晶格常数,以此结构为例进行说明。为了对结构进行数值分析,需要建立严格的边界条件截断波导管,得到有限的计算域。图1中黑色实线围成的区域是该结构的计算域,为建立边界条件,需要在超级晶格的边界上建立特征值问题求解出波导管内的Bloch模,其中由绿色实线和红色实线围成的区域是超级晶格,代表波导管的1个周期。
对于旋磁光子晶体,磁导率μ是一个张量:
(1)
由于旋磁光子晶体和各向同性光子晶体在TM模式下的控制方程相同,不存在特殊的性质,故仅在TE模式下进行研究。对于一个结构在z方向不变、波在xy平面传输的二维问题,它的控制方程为:
(2)
其中:u是电场的z分量;k0=w/c是自由空间波数,c是真空中的波数,w是角频率;n(x,y)是折射率函数。
对于各向同性光子晶体,磁导率μ为常数。此时,TE模式下的Helmholtz控制方程为
(3)
2 单元晶格的DtN映射
图1所示的二维结构中包含3种不同类型的正方形单元晶格,分别是旋磁各向异性单元晶格、各向同性单元晶格和缺陷单元晶格。为了对该结构进行有效数值计算,首先需要构造出这3种不同类型单元晶格的DtN映射。单元晶格Ω的DtN映射Λ本质上是将单元晶格边界Γ上的波动场u映射成边界上波动场u的法向导数,即
(4)
其中:u是控制方程(2)和(3)的解;Γ是Ω的边界;υ表示边界Γ上的单位法向量。
旋磁光子晶体和各向同性光子晶体的区别在于构成材料磁导率的不同,各向同性光子晶体的磁导率是一个常数,而旋磁光子晶体的磁导率是一个张量。旋磁光子晶体在外加磁场的作用下具有各向同性光子晶体不具有的可控性。各向同性单元晶格DtN映射构造过程可以视为旋磁各向异性单元晶格DtN映射构造过程的一个特例。因此,接下来以旋磁各向异性单元晶格(如图2所示)为例来说明单元晶格DtN映射的构造过程,其中介质柱半径为a。

图2 旋磁各向异性单元晶格示意图
单元晶格的DtN映射构造思想是将控制方程的通解写成一组特解的线性组合。对于只包含1个介质柱的旋磁各向异性单元晶格Ω,控制方程(2)和(3)的通解u(x,y)可近似表示成特解的线性组合形式:
(5)
其中:点(x,y)对应的极坐标是(r,θ);φj(r)eijθ是控制方程(2)和(3)的特解;φj(r)用Bessel函数Jj和Yj表示:
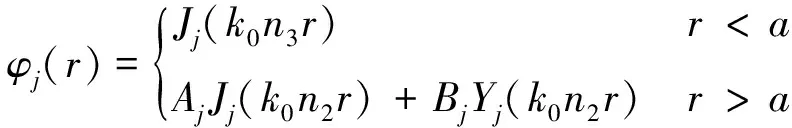
(6)
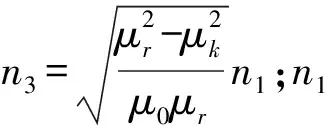
Jj(k0n3a)=AjJj(k0n2a)+BjYj(k0n2a)
(7)
(8)

Λ=BA-1
(9)
假设在单元晶格Ω的每条边上离散N个点,则DtN映射Λ可以近似为一个4N×4N的矩阵。构造完只包含1个介质柱的旋磁各向异性单元晶格Ω的DtN映射后,简要介绍只包含1个介质柱的各向同性单元晶格和不包含介质柱的缺陷单元格晶格的DtN映射构造过程。对于只包含1个介质柱的各向同性单元晶格,其DtN映射构造过程是旋磁各向异性单元晶格DtN映射构造过程的一个特例,此时,P=-1,Q=0,n3=n1,重复式(6)—(9)完成构造。对于不包含介质柱的缺陷单元晶格,P=-1,Q=0,其DtN映射构造过程和各向同性单元晶格的DtN映射构造过程类似,唯一的区别在于特解的表达式φj(r)=Jj(k0nr),此时n=n2=1。
3 超级晶格的DtN映射及特征值问题
构造完单元晶格的DtN映射后,需要构造出超级晶格的DtN映射来建立特征值问题,求解出波导管内的Bloch模。超级晶格的DtN映射M满足:
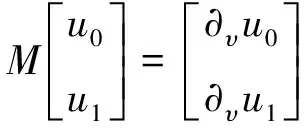
(10)
超级晶格的DtN映射M的构造思想是利用单元晶格的DtN映射和超级晶格内部所有公共边上波动场法向导数连续性,在公共边上建立线性方程组消去公共边上的波动场,从而得到超级晶格的DtN映射M。
图3所示的是图1中由绿色实线和红色实线围成的超级晶格,其中x轴在垂直方向,该超级晶格由m-1个各向同性单元晶格和1个缺陷单元晶格组成,图3中绿色实线Γ0和Γ1分别为超级晶格的下边界和上边界。在超级晶格的左、右两条红色边界(S0P0和SmPm)上采用简单的零Dirichlet边界条件,即波动场u=0。这是因为频率是在带隙范围内选取的,该频率的光波不能在光子晶体中传播,所以在远离波导管处波动场迅速衰减到0。

图3 由m个单元晶格组成的超级晶格(m是奇数)示意图
由于超级晶格内部的每条公共边都位于相邻2个单元晶格的交界面上,故利用2个单元晶格的DtN映射以及这条边上波动场法向导数的连续性建立方程,由此得出m-1条内部边上的线性方程,最终得到1个线性方程组:
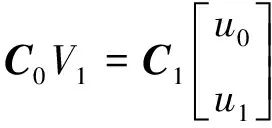
(11)
其中:C0是(m-1)N×(m-1)N矩阵;C1是(m-1)N×2mN矩阵;V1是公共边上的波动场;u0和u1分别是超级晶格下边界Γ0和上边界Γ1的波动场。
另一方面,可以利用每个正方形单元晶格的DtN映射表示超级晶格的下边界Γ0和上边界Γ1波动场的法向导数:
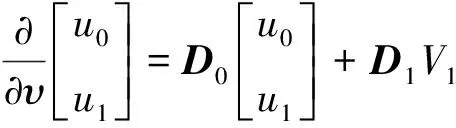
(12)
联立式(11)和式(12)消去V1,得到超级晶格的DtN映射M表达式为:
(13)
其中:M是2mN×2mN矩阵;D0是2mN×2mN矩阵;D1是2mN×(m-1)N矩阵。
构造完超级晶格DtN映射之后,需要在超级晶格2条边界上建立线性特征值问题求解Bloch模。1个Bloch模就是Helmholtz控制方程(3)的1个特解,且满足:
u(x,y)=φ(x,y)eiβx
(14)
其中:β是传播常数;φ(x,y)是在x轴上以晶格常数L为周期的周期函数。利用拟周期条件u1=μu0,∂υu1=μ∂υu0将超级晶格的DtN映射M分成2×2块的分块矩阵,Bloch模由特征值方程(15)解出。
(15)
其中:μ=eiβL是特征值,且该特征值是Bloch波矢函数;I是恒等算子。
4 建立线性方程组
图1中的波导管在x和y方向是无限延伸的,它们起着端口的作用,使光可以进入或离开该结构。在实际数值模拟中,需要在xy平面截断波导管并使用合适的边界条件,因此接下来考虑在光子带隙范围内给定频率下的边值问题。下面介绍如何在切断1根波导管的边界上建立边界条件。
为简化叙述,假设计算域由0≤x≤mL,0≤y≤mL给出,其中L是晶格常数,入射波从计算域左侧的波导管输入。下面以计算域的左侧边界(x=0,0≤y≤mL)为例来说明如何建立截断光子晶体波导管的边界条件。在波导管的1个周期(即0≤x≤L),y方向上包含m个晶格常数。利用求解出的Bloch模,将波导管中波动场展开为
(16)
已知Bloch模是成对出现的,即对于传播常数为β的Bloch模,也存在另一个-β的传播常数。在|μ|≤1中选择合适的β,当|μ|=1时,选择实的β使得Bloch模在x方向上有正的平均功率通量,平均功率通量可通过Poynting向量计算;当|μ|<1时,对应随着x增大指数衰减的Bloch模,确保Bloch模式展开式(16)只包含向x=+∞传播的模和随着x增加而衰减的模。波导管内的波动场分为向前传播的波动场和向后传播的波动场,即u=u++u-。其中
(17)
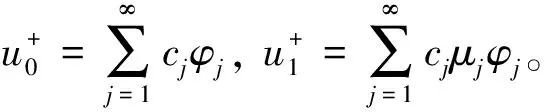
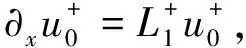
(18)
同样地,得到x=0处u-的边界条件为:

(19)
根据u=u++u-和式(18),式(19)消去u-得到x=0处边界条件为:
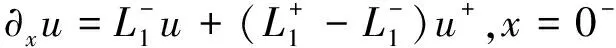
(20)
其中u+是入射波。对于计算域的另外3条边界,由于这3条边截断的波导管内只有输出波,故在构造其边界条件时,不需考虑入射波情况,3条边的边界条件为:
(21)
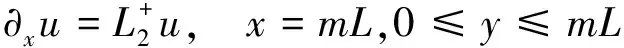
(22)
(23)

对于图1所示的计算域,需要写出计算域中每个单元晶格边界上波动场u的线性方程。为建立线性方程组,分别在计算域的内部和边界上建立线性方程。对于计算域内部的每条边,由于这条边位于2个相邻单元晶格的交界面上,这时利用2个单元晶格的DtN映射以及这条边上波动场法向导数的连续性建立方程。对于计算域边界上的边,利用单元晶格的DtN映射、截断波导管的边界条件和这条边上波动场法向导数的连续性建立另一个方程。最终得到包含所有边上波动场的线性方程组:
AX=b
(24)
其中:X为截断域内所有边上波动场的列向量。若单元晶格每条边离散N个点,则系数矩阵A的大小为2(m+1)mN×2(m+1)mN。内部边的每个方程只和2个相邻单元晶格其余的少量边有关,因此A是一个稀疏矩阵。最后求出传输和反射光谱。
5 数值算例
以四端口旋磁光子晶体环形器和波导交叉结构为例来验证算法有效性。所有结构均由旋磁光子晶体和各向同性光子晶体组成,且这些光子晶体均由相应材料制成的介质柱在空气中按照正方形点阵排列构成。选择从左侧波导管输入的传输模为入射波,并分别计算左侧端口的反射率和右侧、上侧、下侧端口的传输率。

以表1和表2为例来说明超级晶格层数m和单元晶格每条边上离散点数N的选取过程。选取图4中的点A1对应的频率wL/(2πc)=0.365 8来进行说明:固定超级晶格层数m,改变单元晶格每条边上离散点数N;固定单元晶格每条边离散点数N,改变超级晶格层数m。

图4 算例1结构传输和反射光谱

表1 固定超级晶格总数m改变单元晶格边界上的点的个数N

表2 固定单元晶格边界上的点的个数N改变超级晶格总数m
从表1和表2可以看出,当m=15,N=11时,计算结果具有4位有效数字。
频率为wL/(2πc)=0.357 1、wL/(2πc)=0.361 6和wL/(2πc)=0.372 8的电场图见图5。 3个频率分别对应能量从端口A、B和C输出的最大透射率。从图5(a)可以看出,当频率为wL/(2πc)=0.357 1时,大部分能量从A端口定向输出。由于单向波导的存在,能量从左侧D端口输入后,在第1个交叉口处只能向其中1个方向转向,此频率下在A端口定向输出。图5(b)给出了频率为wL/(2πc)=0.361 6时的电场图,能量主要从B端口输出。同时给出了频率为wL/(2πc)=0.372 8时的电场图,如图5(c)所示。可以看出,大部分能量从C端口定向输出。
算例2的结构如图6(a)所示,为波导交叉结构[8]。该结构中有4根YIG棒位于十字交叉口处,YIG棒半径a2=0.19L,其余半径a1=0.2L。为了得到4位有效数字,选取包含15×15个单元晶格的计算域。该计算域包含480条边,取N=11,得到如图6(b)所示的传输和反射谱,计算结果与文献[8]中结果一致。从图6(b)可以看出,当频率为wL/(2πc)=0.366 0时,A端口的透射率高达0.97,该频率下的电场图如图6(c)所示。可以看出,当能量从左侧D端口输入时,大部分能量从A端口输出。

图5 不同频率电场图
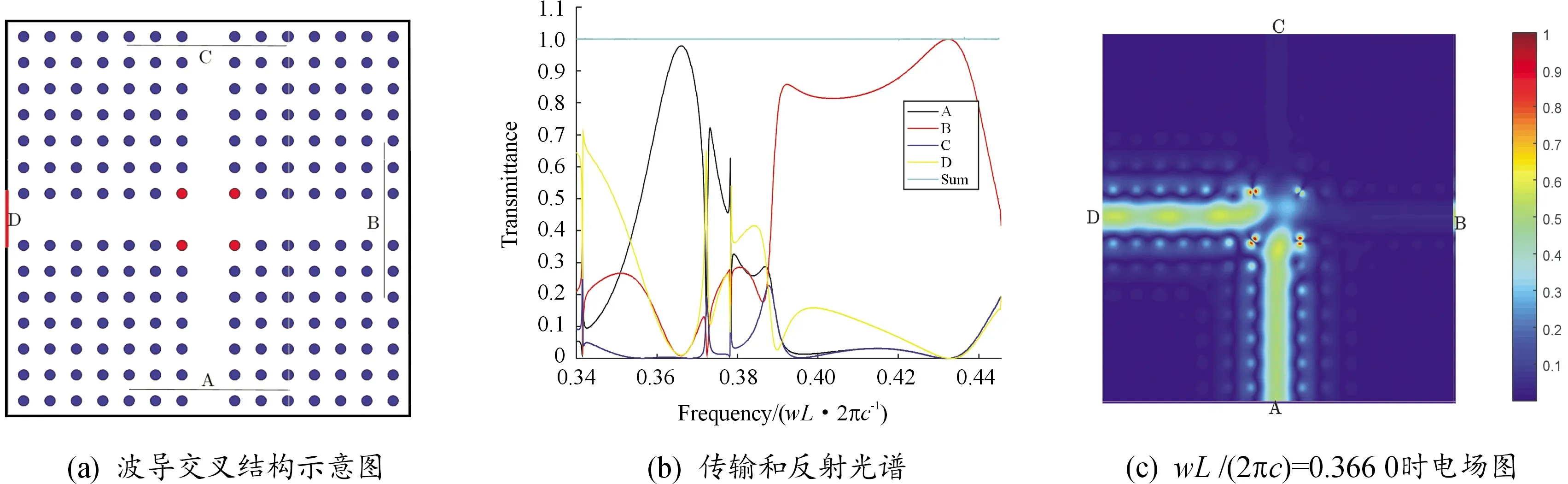
图6 算例2结构和相关图谱
6 结论
扩展了DtN映射的方法,将其用于计算二维旋磁光子晶体元件的传输和反射光谱。DtN映射方法只需在计算域边界上进行离散,减少了未知数,最终得到包含计算域中所有边上波动场的线性方程组。该线性方程组的系数矩阵是稀疏的,系数矩阵规模小,计算速度快,有利于计算二维旋磁光子晶体元件的传输和反射光谱。研究对象均为介质柱截面为圆形的二维旋磁光子晶体结构,方便进一步研究介质柱截面非圆形(如椭圆形、三角形和六边形等)的旋磁光子晶体结构。对于介质柱截面为圆形的光子晶体结构,采用柱面波展开法来构造单元晶格的DtN映射,但对于介质柱截面非圆形的光子晶体结构,该方法不再适用,此时单元晶格的DtN映射可通过边界积分方程方法来重新构造。由于主要研究z方向上不变的二维结构,因此下一步将考虑用垂直方向模展开法来计算三维结构。

