刨花振动筛运转工况下主结构振动应变测试与分析

张涛，卢峻达，许林云，周杰，张超，姜东，杭晓晨，刘军

(南京林业大学机械电子工程学院，江苏 南京 210037)

近20年来，振动筛作为最有效的一种物料粒度分类机械，结构稳定可靠、效率高、处理量大，被广泛应用于各种物料的分离、分级以及杂质的筛选[1-2]。同时，为了进一步提高筛分的速度和效率，国内外研制的振动筛开始向大型化、重型化和标准化的方向发展。随着振动筛结构加大、振动强度增加，对机械结构强度和刚度的要求也相应提高，筛体所需要的激振力、参振质量和动载荷也相应增大，经常导致振动筛结构强度和刚度不足，引起振动筛筛体变形、横梁或侧板断裂、焊缝开裂等，从而缩短振动筛的使用寿命。国内对振动筛分设备的研发和设计起步较晚，设备参数和使用寿命与国外同类型产品相比有较大差距，仍需要对此方面进行深入研究[3]。

筛箱作为振动筛的重要组成部分，在强大的交变激振力作用下很容易发生疲劳破坏。大量学者对各种型号振动筛进行了动强度研究，Slepyan等[4]针对矩形振动筛质量受到自平衡作用产生共振和振幅非线性限制问题，建立了动力学模型，基于系统动力学特性估算了受自平衡作用过程下的能量耗散，能够有效减轻矩形振动筛抖动问题。孙玉涛等[5]对ZK3648振动筛的横梁进行数值仿真，对不同横梁结构进行优化设计，通过比较静力学和动力学数值仿真的计算结果，依据横梁截面抗弯模量相等原则确定了最佳的横梁结构形式，为横梁的优化设计提供了思路。

图1 刨花振动筛结构Fig. 1 Structure of particle swing screen

上述研究多是针对煤矿行业大量使用的直线振动筛进行分析的，这种类型的振动筛利用安装在筛体侧板处的偏心激振器带动激振轴激振，产生的激振力强迫筛体做近似直线往复运动[6]，大型刨花振动筛则是采用摆动筛的结构形式，通过驱动装置带动筛箱底部中心位置处的偏心轴旋转，迫使筛箱进行摆动运动[7]。实际上大型刨花振动筛长期处于工作状态下，工作部件多，筛箱作为振动筛的主体部件，振动受力更为复杂，相较其他部件也更易出现损坏[8]。本研究依据刨花振动筛的结构特点，以某公司研制的BF14260刨花振动筛(以下简称振动筛)为研究对象，运用电阻应变测量法测试振动筛筛箱的力学性能，得出振动筛筛箱整体应变分布规律，以期为降低刨花振动筛整体应变提供参考。

1 刨花振动筛工作原理与存在的问题

1.1 刨花振动筛工作机理

BF14260刨花振动筛整体尺寸为8.8 m(长)×4.5 m(宽)×5.5 m(高)，质量约10 t，最高工作振幅为30 mm，最大回转速率为175 r/min，工作回转速率为165 r/min，其主体结构由进料箱、出料箱、筛箱和支撑腿等组成，如图1所示。筛箱为长方体箱式结构，以进料箱为前、出料箱为后确定方位，去除筛箱门板与覆盖板后的筛箱骨架如图1b所示。因左右两侧对称分布，只对左侧骨架主支承梁进行命名说明其构成，即由3条竖直方向布置的竖梁A、B、C，以及3条水平方向布置的横梁A、B、C构成。3条竖梁采用同一型号的方钢，而3条横梁则由上到下横截面尺寸按照80，120和150 mm的方式布置，便于承受整体静动态应力。4个支撑腿分别与左右两侧前后4个竖梁相连，支撑整个振动筛的质量，同时约束振动筛在偏心振幅激振下只能以平面振动形式响应。支撑腿采用ROSTA公司的AK系列弹柔性支撑腿，内置橡胶起弹性与阻尼作用，可较好地消耗振动筛传递给基座的振动能量，从而在一定程度上保护振动筛的基础结构[7]。筛箱内部由上下两层分选室组成，两分选室结构完全相同，每层分选室内装有3层筛孔直径不同的筛网，使混合在一起的刨花经筛箱分选后形成4级不同规格的刨花，上下两层经分选后对应的同种规格刨花再通过同一出料通道出料并输送出去。

刨花振动筛的动力驱动装置如图2所示，动力由驱动电机→带轮→主传动轴→偏心传动轴→X型板传动，X型板的4个伸出端(图1b)与靠近4个支撑腿的筛箱主骨架下端内侧框架相连，从而将偏心振动传递给振动筛。偏心距可通过调偏装置调节，偏心振动频率可通过电机转速调节。

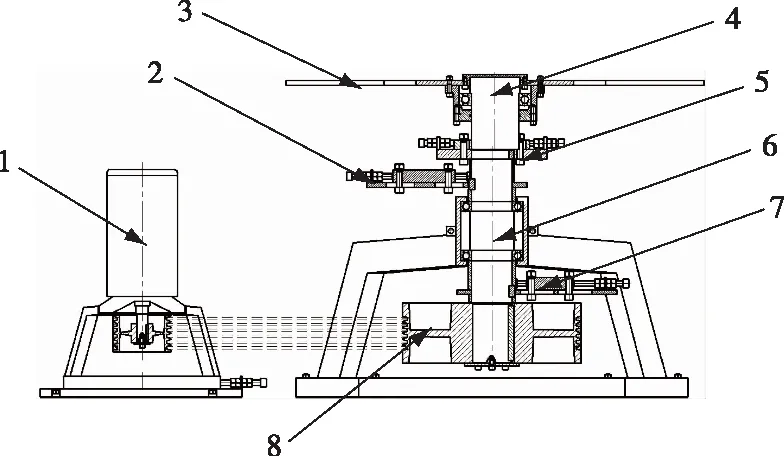
1.驱动电机；2.配重块a；3.X型板；4.偏心轴；5.调偏装置； 6.主传动轴；7.配重块b；8.带轮。图2 振动筛驱动系统Fig. 2 Vibrating screen drive system

1.2 刨花振动筛存在的问题

BF14260刨花振动筛整机质量约为10 t，其中振动体部分的质量约为7.5 t，其余主要为4条支撑腿和动力传动装置的质量。该型号振动筛工作振幅最高为30 mm，回转速率最高为175 r/min。振动筛由于质量较大，且振动筛的动态平衡性不易控制，当偏心振幅超过30 mm或振动频率高于175 r/min 工作时，振动筛会发生较强烈的抖动，甚至支撑腿与地面接触处会产生周期性跳动现象，致使振动筛无法正常工作，同时也极易导致振动筛的疲劳寿命过短，产品整体耐久性寿命过短，影响产品的使用性能[9]。由图2可知，振动筛是由驱动系统带动X型板运动进而推动筛箱的，X型板与筛箱横梁A焊接连接，因此X型板在推动筛箱运动时是通过迫使横梁A位移，进而使整个筛箱进行筛分运动，横梁A应为筛箱上应变最大的位置。国产类似结构的刨花振动筛在长时间不间断工作下发生疲劳破坏产生裂纹，并在裂纹表面焊接连接板与辅助加强筋进行补救处理的情况见图3。从图3中可以看出，发生裂纹破坏的位置出现于横梁A与各竖梁连接位置处，并且发生在横梁上。国外同类型的振动筛转速可达200 r/min，最大振幅可达40 mm，因此不分析主龙骨出现裂纹破坏的关键因素，会严重制约该振动筛的寿命和产能。

图3 横梁A裂纹破坏情况Fig. 3 Crack failure of Beam A

2 应变试验与方法

2.1 测试方法与装置

分析机械结构振动时各零件的强度或疲劳特性，最直接最可靠的方法是在构件的关注点上粘贴电阻应变片，测试其应力或应变变化关系[10]。本研究中的振动筛因疲劳破坏裂纹主要发生在横梁A上，则应变测点也应布置在该横梁侧表面上，如图4a所示。为消除温度变化的影响，采用同种电阻值的电阻应变片作为温度补偿片连接到电桥电路中[11]，如图4b所示，并连接成惠斯通半桥双臂电桥电路结构形式。

图4 应变测试实物Fig. 4 Physical images of strain tests

应变测试系统由DH5922D动态信号采集装置和DHDAS动态信号采集分析系统(江苏东华测试技术股份有限公司)构成[12-13]。每次试验前均需对DHDAS动态信号采集分析系统进行调零处理，试验时通过无级变速器调整振动筛从零转速到工作转速(165 r/min)，稳定运转一段时间后逐步减速并断电，记录振动筛从启动到稳定，再到停机的整个时间过程，试验重复3次[14-16]。

2.2 试验方案与测点布置

2.2.1 横梁A主体疲劳破坏区测点布置

虽然在横梁A上极易出现疲劳破坏裂纹，但无法断定横梁最大应变出现在哪个方向上，因此先在横梁A上处于竖梁A与B之间的区段上采用应变花(图4c为其中一个测点粘贴的应变花结构形式)进行测试。试验共布置12个测点，如图5a所示，其中测点1、2、3与测点7、8、9在该区段内对称布置，测点4、5与10、11对称布置。在整个横梁龙骨两侧面均覆盖了一层钢板通过焊接连接，且在覆盖钢板上对应横梁位置处开了多个长槽孔，用于加强钢板与横梁的焊接连接。该区段内12个测点中，长槽孔处的测点5与11均是将电阻应变花直接粘贴在横梁A表面上，其余各测点处的电阻应变花均为粘贴在横梁A侧表面对应位置的钢板上。因筛箱以倾斜5°的角度安装便于刨花在筛网上实现自动进料与分级功能，因此无论是横梁还是竖梁在实际工作时均处于倾斜状态，但本研究中的测点分布相关图均以横梁水平方向、竖梁垂直方向表示。本研究设沿横梁A长轴方向为x方向，沿竖梁长轴方向为z方向，与x及z方向夹角45°方向为t方向，正好对应电阻应变花的3个测试方向，如图4c与d所示。

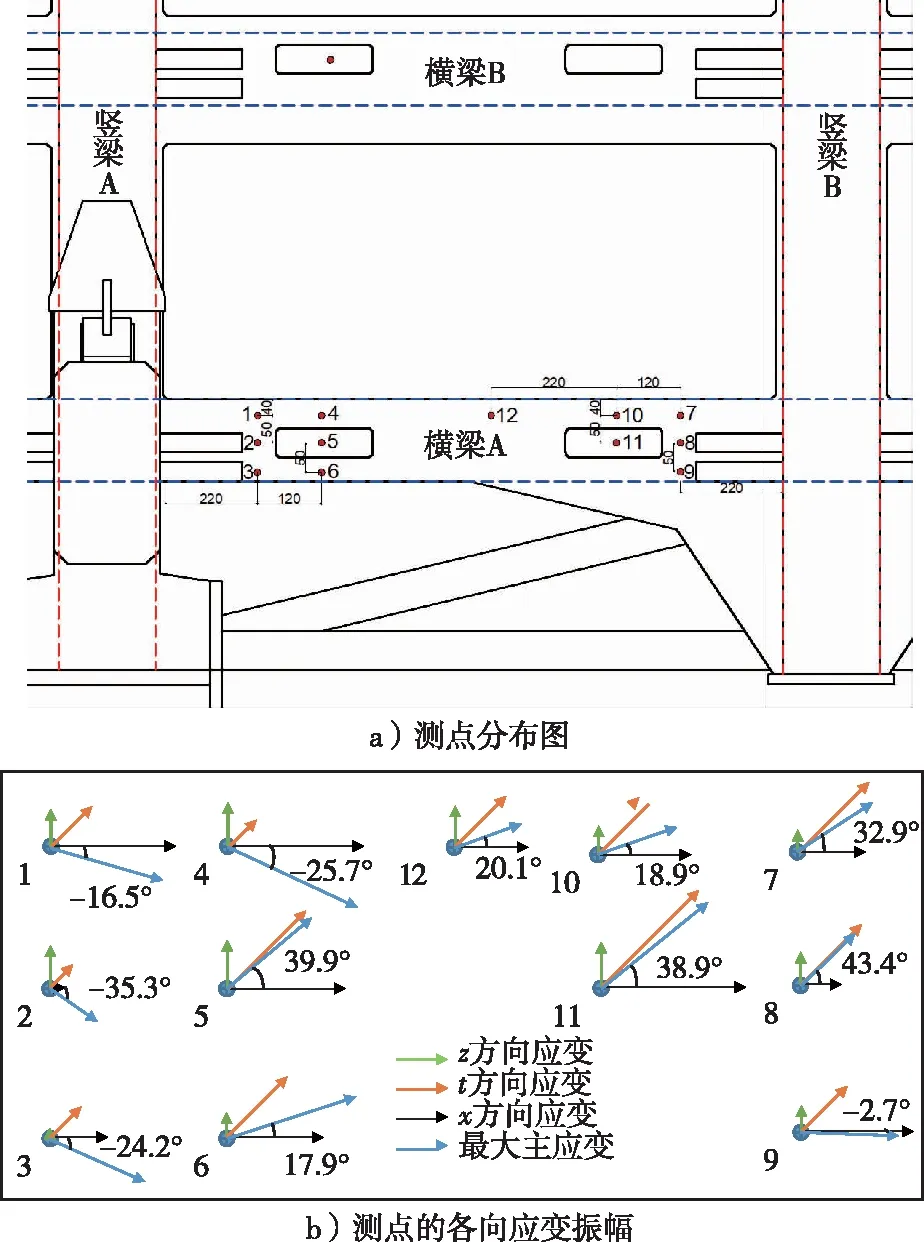
图5 主体疲劳破坏区测点及应变分布Fig. 5 Measured points and strain distribution of the main body fatigue failure zone

2.2.2 横梁A整体应变分布测点

在研究横梁A整体应变的试验中，将测点均布置在长槽孔内，即均为测取横梁A梁体侧表面上的应变情况。每相邻两个竖梁区段内及区段外横梁A上均布置2个测点，共8个测点，从左到右顺序依次为测点13、14、5、11、15、16、17和18，如图6所示。

图6 侧面横梁整体测点分布Fig. 6 Distribution of overall measuring points on the side beam

2.2.3 单侧所有横梁应变分布测点

虽然疲劳破坏裂纹极易出现在横梁A上，但各横梁上的应变分布情况还需作比较分析，从而为研究振动筛疲劳破坏原因及振动筛结构重新优化设计提供试验数据。因此，在横梁B与C上各布置2个测点19、21及20、22，分别与横梁A上的测点5与16相对应，如图6所示。

3 结果与分析

3.1 启停全过程动态信号分析

刨花振动筛测点5在x方向启停全过程中的典型应变情况如图7所示，可将启停全过程分为5个阶段：调零阶段、启动阶段、加速阶段、稳定阶段和停止阶段。调零阶段：刨花振动筛处于待命状态，每次测试开始前均进行调零。启动阶段：缓慢低速启动电机，带动刨花振动筛开始运转，由于振动筛的启动力矩较大，只要一启动，应变信号就会出现突变，且应变幅值出现比较剧烈的波动，然后逐渐减小并趋于稳定，该测点信号稳定在3.2με。加速阶段：随着电机转速不断提高，测点应变振幅也随之增大。稳定阶段：当电机转速增至165 r/min 并稳定在该转速时，测点应变幅值稳定在(-9.3～13.5)με范围内，作周期性简谐变化。停止阶段：电机断电，刨花振动筛逐渐减速到停止，测点应变的振幅逐渐减小，直到最后完全停止；在电机断电的瞬间，测点应变幅值的中心(即均值)位置会突然降至零值附近，说明刨花振动筛在振动工作过程中支承横梁上会附加一恒定偏置应变，只要振动停止，偏置应变就会消失。

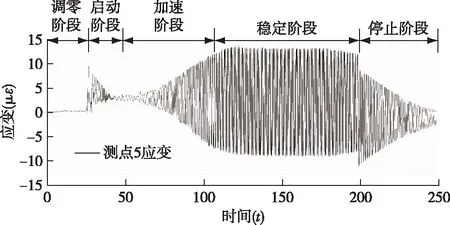
图7 振动筛的测点5在x方向启停全过程的应变情况Fig. 7 The strain situation of measuring Point 5 of the vibrating screen in the whole process of start and stop in the x direction

3.2 横梁A主体疲劳破坏区

在横梁A主体疲劳破坏区内均采用3片直角形电阻应变花进行测量，应变花的3个测试方向分别对应横梁上的x、t和z方向，对稳定阶段的信号进行处理可得各测点的应变振幅与均值，如表1所示。

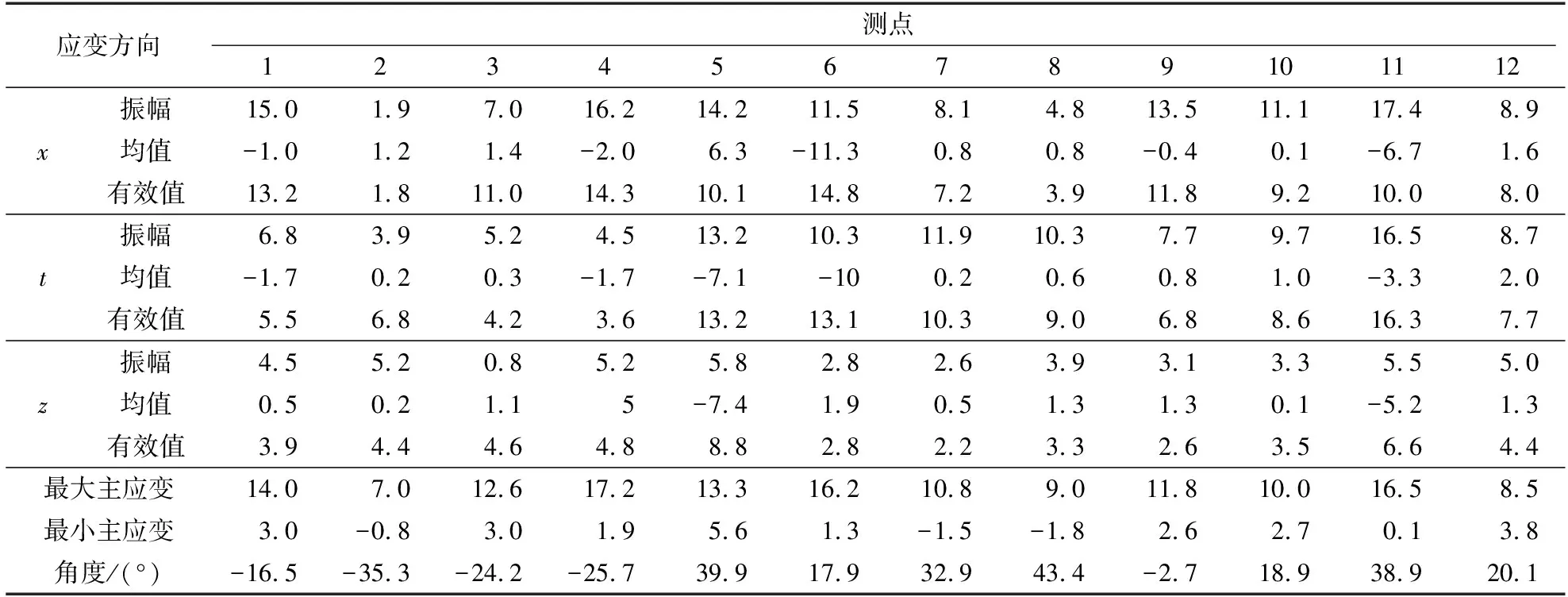
表1 横梁测点应变值Table 1 Strain value of measuring point of beam με

3片直角形应变花主应变ε和主应变与x方向的夹角α可由式(1)和(2)计算。应变花沿x、t、z方向测试的应变分别对应ε0、ε45、ε90，且各值均取稳定阶段应变信号的有效值。

主应变：

(1)

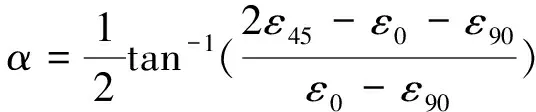
(2)

将所有计算结果全部列入表1中。各测点各方向的应变振幅，包括最大主应变和夹角α如图5b所示。

比较测点1、2、3的应变数值可知，位于横梁上下边缘上的测点1和3的x方向应变振幅均明显大于其他2个方向，测点1达到最大振幅15.0με，而中间测点2的x方向应变值非常小，只有1.9με。同时，与测点1、2、3相对应的测点7、8、9，其x、z方向也表现出与测点1、2、3一致的现象，如果只考虑x方向的应变，横梁A具有横向弯曲交变振动的特点，但测点7、8、9处斜向45°的t方向应变值又明显较大，说明横梁A还存在较大的剪切应变。测点1、2、3的主应变方向处于-16.5°～-35.3°范围内，而测点7、8、9的主应变方向处于-2.7°～43.4°范围内，因此各位置点的主应变方向相差较大。

对于左侧第2列测点4、5、6，因测点5直接粘贴在横梁A的表面上，可直接反映横梁A上的应变情况，测点4、6与测点1、2的应变值基本一致，只是测点6的t方向应变较大，达到10.3με，而对于直接反映横梁表面应变的梁中间测点5明显表现出与测点2、8不相同的数值，x与t方向的值均明显较大，分别达到14.2με和13.2με。同样对于右侧第2列的测点11，其也为横梁A上的点，同样沿x与t方向呈现出在所有测点中的最大值，分别为17.4με和16.5με。

根据以上分析，实际横梁A侧表面上下边缘处的应变值应远大于覆盖钢板上对应测点的值。

3.3 横梁A总体应变分布关系

通过对横梁A主体疲劳破坏区的12个测点测试结果分析，所有测点的z方向应变振幅均较小，因此在分析横梁A总体应变分布时，只考虑x方向应变，且将所有测点均布置在横梁A上所有槽孔位置处，共8个测点，其应变均值、振幅如图8a所示。主要应变区在3个竖梁之间，即应变发生在2个支撑腿之间的4个测点5、11、15、16处，支撑腿之外4个测点13、14、17、18的应变全振幅为5.8με～8.9με，而中间区段4个测点的应变全振幅高达28.3με～36.2με，且测点11、15、16的全振幅值明显大于测点5。中间区段4个测点的均值差别也较大，且不是所有测点经过调零后启动时应变均值均呈现如图7所示的向正值跳动突变的现象，有些测点会向负值跳变。测点5向正值高跳6.3με应变值，而测点11又向负值深跳6.7με应变值；测点15与16均以小幅值正向或负向略微跳变。

3.4 单侧所有横梁应变分布关系

横梁A、B、C上的2列6个测点5、19、20及16、21、22的x方向应变值如图8b所示。横梁A上2个测点的应变值均最大，最上端横梁C上应变值次之，其测点20、22分别比横梁A上的测点5、16的应变值低23.0%和49.2%；中间横梁B应变值最小，测点19与21的应变全振幅只有8.5με和13.6με，远低于横梁A与C的应变值。

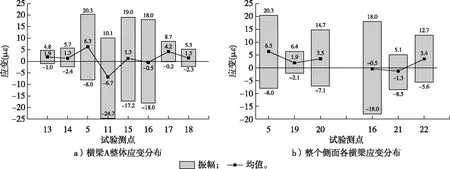
图8 横梁测点x方向应变均值与全振幅Fig. 8 The mean value and full amplitude of the strain in the x direction at the measuring point of the beam

3.5 应变信号相位差

单一测点1、2的3个方向应变信号随时间变化的曲线见图9。以x→t→z的方向顺序，测点1、2各方向之间分别滞后65°→120°和63°→229°。图9c为测点1、2、3沿x方向的应变信号随时间变化的曲线，横梁A同一横截面上3点既不同相也不反相，而是从上至下出现一定相位负差，即测点2比测点1、测点3比测点2的相位均滞后约15°。图9d为横梁A表面覆盖钢板上接近横梁上边缘的从左至右5个测点1、4、12、10、7沿x方向的应变信号曲线，呈现出各测点的应变相位从左至右逐步滞后的现象，但与各几何位置点与旋转中心，以及夹角与应变信号滞后角度并无完全一致的对应关系。

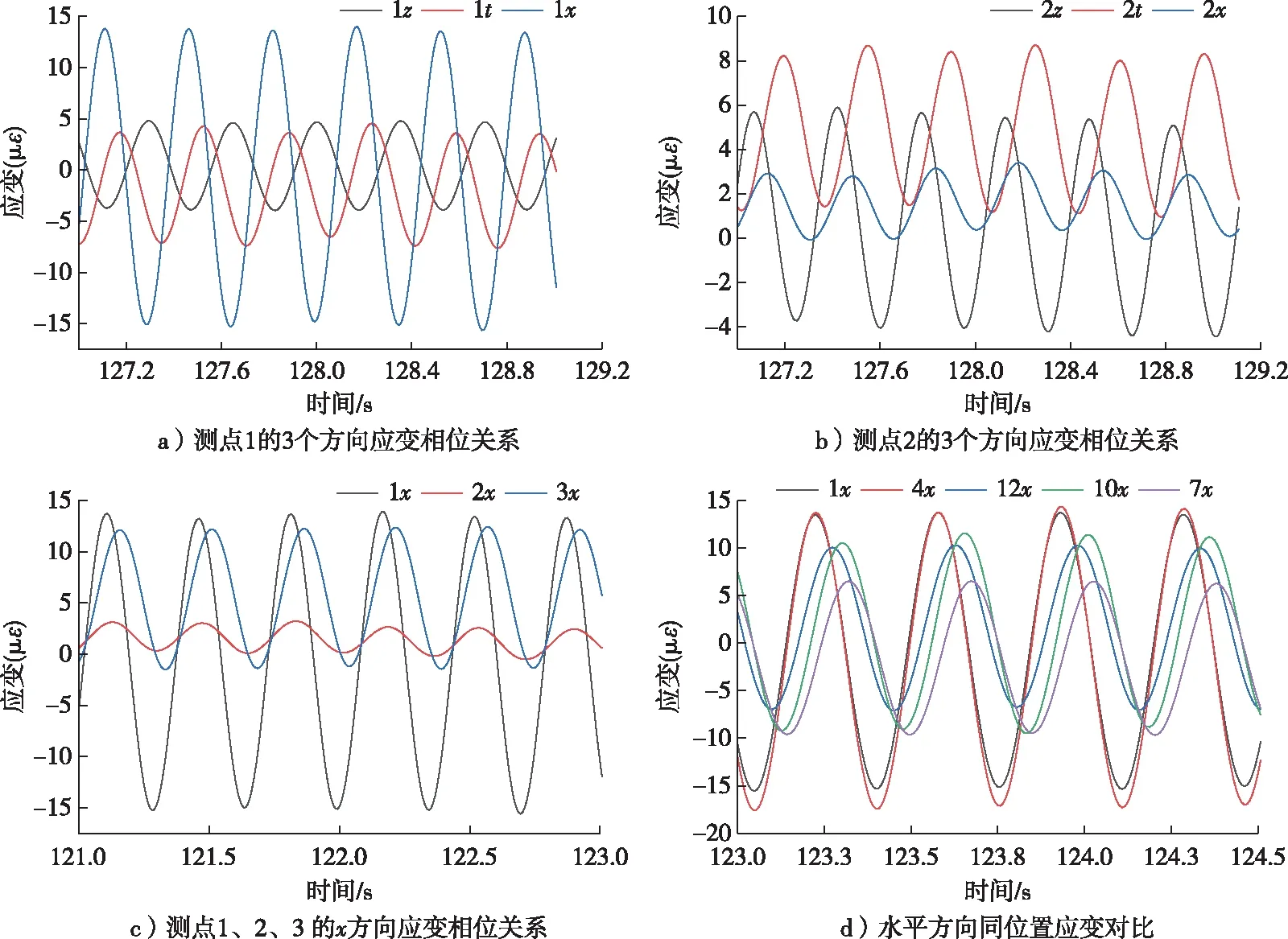
图9 测点相位关系Fig. 9 Phase relationship of measuring points

3.6 结果与讨论

测试结果分析说明，前后支撑腿之间的横梁A上存在较大应变。梁体不仅存在横向弯曲交变应变变化，还存在剪切应变变化，同时因横梁内外两侧均覆盖钢板焊接连接，横梁A上部钢板开了大窗口用于安装门板，下部又连接了结构复杂的各种小型支撑梁，左右两侧龙骨之间又连接了各种支撑梁，因此横梁A的受力结构非常复杂，致使各测点三向应变信号、各测点同向应变信号之间均存在不同的相位关系，使得瞬时主应变与方向一直在变。横梁A所用材料为Q345，弹性模量为206 GPa，其最大应变值为-24.7με，计算可得横梁A在运转过程中承受的最大压应力约为5.1 MPa。同时，因主梁结构上覆盖了钢板，本研究只能测取横梁A中心处表面的应变，无法测取横梁上下边缘处的应变值，从而无法真实反映横梁A整体实际表面应变分布情况，因此有待于采用仿真模拟方法或其他方法进一步分析研究。受到试验条件限制，本研究未能进行振动筛的共振测试，后续将会对刨花振动筛进行进一步研究，通过改变设备结构、偏心距及频率等参数，研究其对刨花振动筛运转过程的影响。

4 结 论

1)电机启动后，各测点会增加正向或负向偏置静态应变，停机后偏置静态应变会消失。

2)横梁A表面的钢板上，接近横梁A上下边缘处的应变值明显大于中间位置处的应变值，且主要以水平方向和斜向45°应变为主，而垂直方向应变值均较小，即横梁A主要承受横向弯曲及剪切交变应变。

3)整体3根横梁上应变最大的为横梁A，同时横梁A上应变最大位置出现在前后支撑腿之间，这与通过传动原理分析出的最大应变位置一致，该区域内极易产生疲劳破坏的现象。

因此，整体支撑梁龙骨结构应重新进行优化设计，通过减小横梁两侧尺寸并加强横梁支撑腿间的结构，进一步降低横梁A最大应变区域的应变值，同时应适当调整横梁B的位置以提升横梁B的应变承受能力。