BP-Garson算法的高桥隧比路段交通事故预测研究
曹雪娟,黄铭轩,吴博文,杨晓宇
(重庆交通大学 a.材料科学与工程学院; b.土木工程学院, 重庆 400074)
因自然环境复杂性,山区高速公路的修建通常会应用到大量隧道、桥梁等构造物。其中,桥隧比例较高的道路路段可被称为高桥隧比路段,本文将桥隧比定义为:桥隧比=(桥梁里程+隧道里程)/路段总里程。隧道、桥梁等构造物的修建虽然有助于高速公路顺利通向各个地区,但桥隧相连、坡陡弯急和持续长大纵坡等路段的交通事故率仍然高居不下[1]。山区高速运营安全形势严峻,交通事故的发生不仅会给驾乘人员带来诸多不便,严重时还会造成人身安全问题。此外,各山区高速公路常常作为物资运送的大动脉,交通一旦中断,群众的生产生活就会受到影响。为降低山区高速公路交通事故发生率,利用已有交通事故数据对交通事故各因素的内在关系进行分析具有重要意义。路面路表性能是影响交通事故的重要道路条件,尽管学者们已对此做出相关研究,但是路表数据获取困难、处理复杂,使得研究进展受限[2-4]。
研究表明,采用人工神经网络算法对路面路表性能的数据点进行非线性映射逼近处理,可以实现性能参数的有效整合。Garson算法能够调用权重矩阵对构建的预测模型进行重要性分析,得到输入参数与输出参数的权重关系。因此,本文采用BP神经网络算法和Garson算法,依托路面养护数据建立高桥隧比路段的交通事故预测模型。采用监督分类法分析高桥隧比路段的交通事故数据,研究路面路表性能参数对高桥隧比路段交通事故的影响,并为山区高速公路交通事故预防及路面养护建设提供建议。
1 研究方法和理论基础
1.1 基于R语言的BP-Garson组合算法
R语言平台因其结果可视化,依托其实现的神经网络已被应用于各种研究领域[5-7]。误差逆传播算法(error back propagations,BP)是神经网络中的一种常用类型,也称为BP神经网络,该算法理论清晰且适合非算法研究工程设计人员使用[8-11]。神经网络结构如图1示。Garson算法将网络结构中的每个输入信号间的连接权值作为“桥梁”,通过权值矩阵计算出每个输入参数对输出参数的相对贡献值。

图1 BP神经网络结构示意图
1.2 监督分类算法
常见的文本分类算法有无参数型的朴素贝叶斯[12]、决策树法[13]、支持向量机[14]等。在实际应用中,监督分类算法能较好地解决许多量大复杂的分类工作,基于文本数据利用监督分类算法进行分类器设计的研究成果丰硕。在监督分类中,首先需要一定数量的原始训练样本,通过参数统计得出每一类别的统计特征量,并用某种分类算法对其进行训练得出分类模型,最后利用该模型对整个原始数据进行分类。
2 数据预处理和评价方法
2.1 研究参数的预处理
2.1.1路段划分和数据采集
高速公路路段划分有几种常用方法[15],其中定长法以高速公路里程桩为划分路段的依据,确定一定长度的路段,将全线划分为连续的等长路段单元。本文研究段的地理位置如图2所示,起讫点桩号为K1672+332~K1995+666,路段全长约324 km,桥隧道总长为181 km,路段总体桥隧比约56%。以每公里作为一个路段进行划分,对采集数据进行处理,分别得到路面行驶质量指数(RQI)、路面横向力系数(SFC)和路面车辙深度指数(RDI),如表1所示。
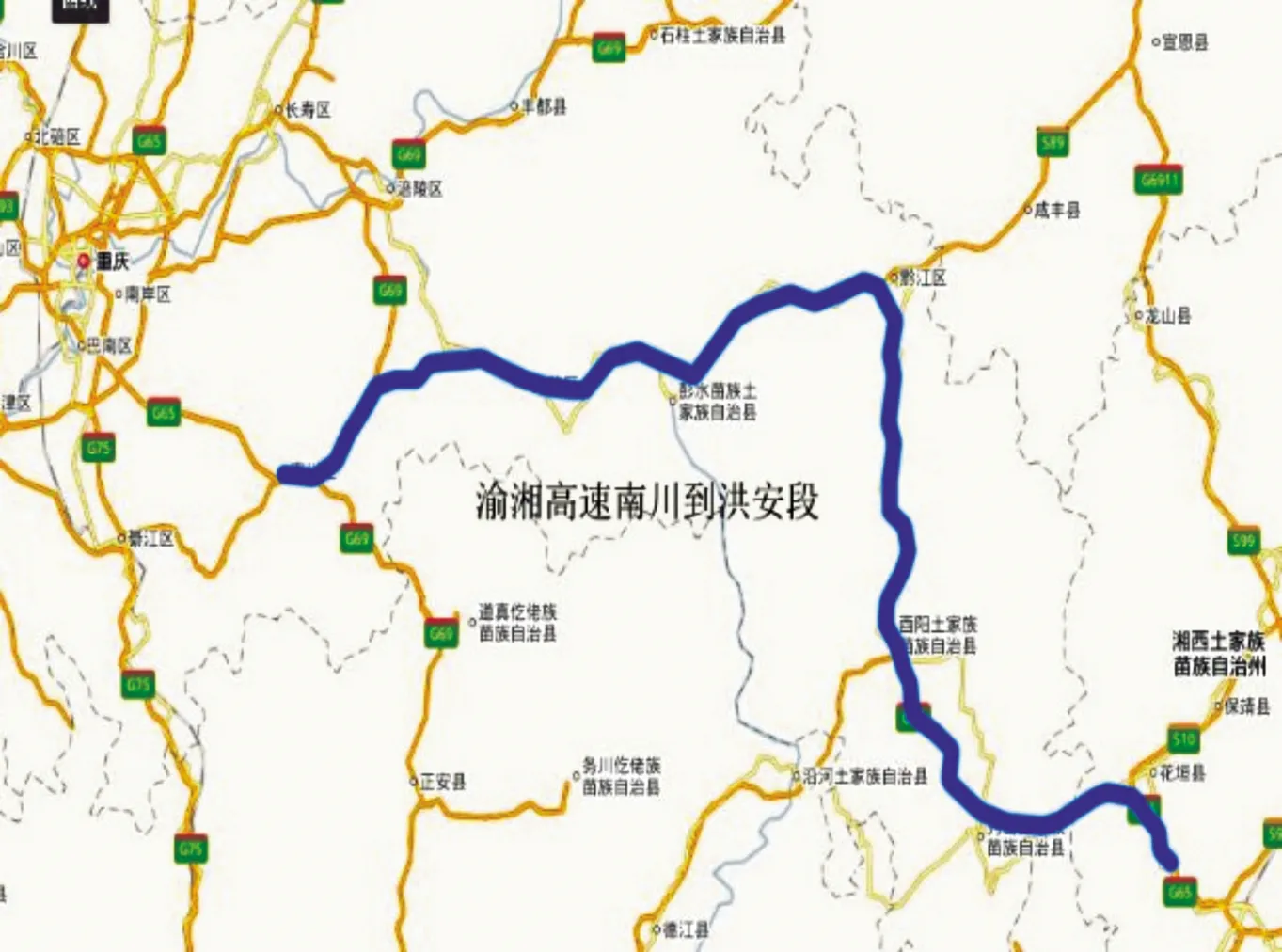
图2 具体研究段地理位置示意图
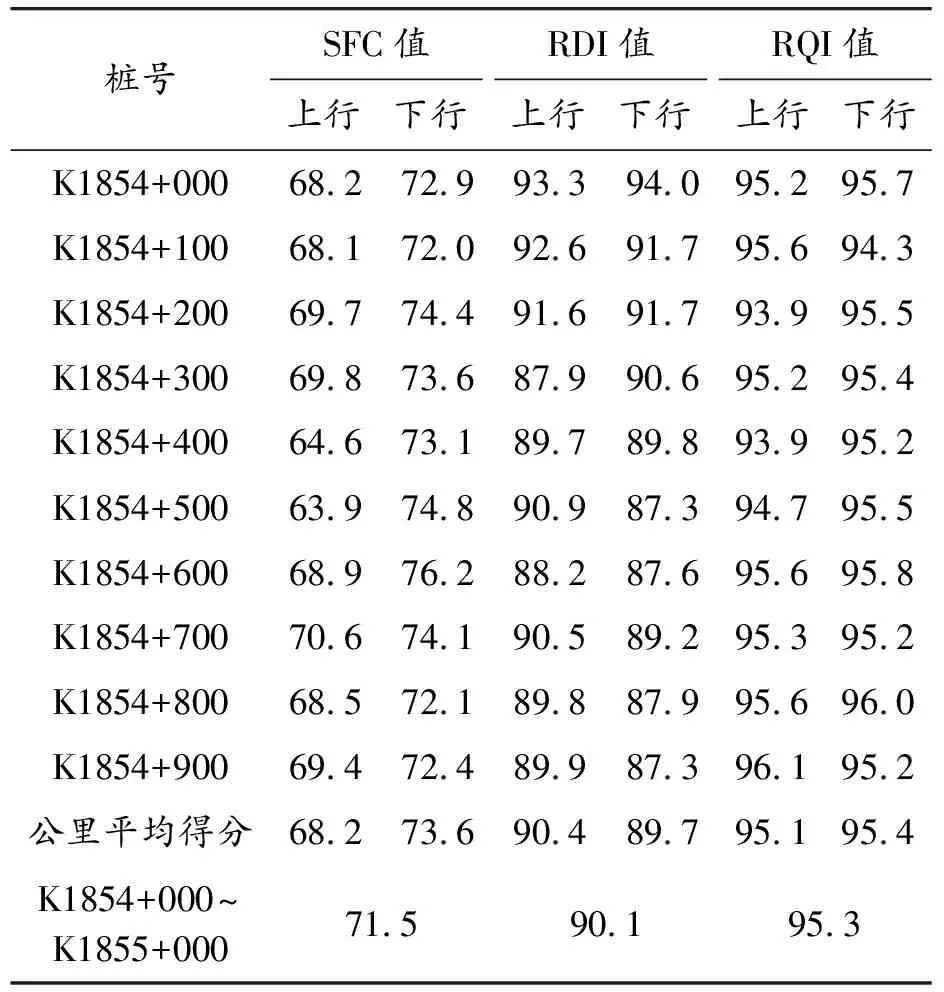
表1 每公里路面路表采集数据的数据预处理(数据节选自2015年)
2.1.2输入参数的归一化处理
为了优化神经网络的训练建模,需要对原始数据预处理后得到的输入参数进行归一化处理,这样既能使原始数据无量纲化,又能减少参数量级不同对结果造成的影响,计算公式如下。
(1)
2.1.3输出参数的二值分类
分类监督算法的核心在于对文本词义进行正确的抽象处理,使算法输出的结果有效。本研究采用逻辑回归统计特征量的二值分类思想,抽取事故路段中频繁出现的桥隧段作为研究对象,将桥隧段发生的交通事故作为输出记为1,非桥隧段的交通事故输出记为0。
2.2 基于混淆矩阵的预测模型评价
2.2.1基于混淆矩阵的量化模型评价
为了量化评价模型的拟合效果,二值分类系统中常用评价指标有准确度、精确度和召回率。基于混淆矩阵对二值分类(ture or false)模型进行评估,准确度(Accuracy,ACC)越接近1则表示模型越优。混淆矩阵及模型的评价公式如表2和式(2)—(4)所示。精确度(precision)用于评价预测结果,用来表示预测为真的样本中正样本的数量。召回率(recall)用于评价模型预测时原始样品的选择情况,表示样本中的正例被预测正确的数量。
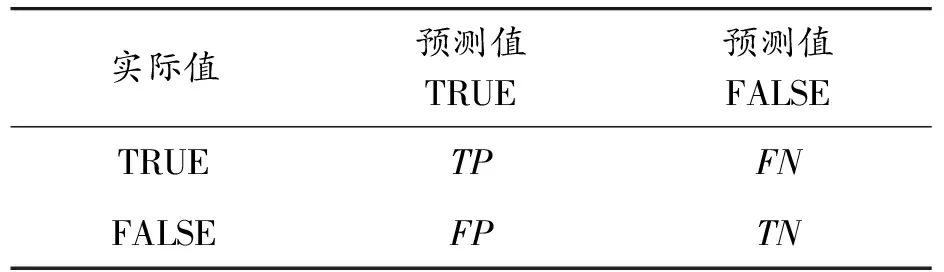
表2 二值分类的混淆矩阵
(2)
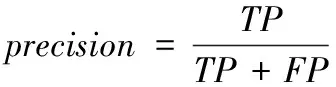
(3)
(4)
2.2.2受试者工作特征曲线
受试者工作特征曲线(receiver operating characteristic,ROC)是利用图形可视化方法来展现二值分类系统预测能力的一种评价手段。通过式(5)绘制真阳性比例(ture positive rate,TPR)-假阳性比例(false positive rate,FPR)图,利用传统模型分析的灵敏度(Y轴)和特异性(X轴)综合反映预测模型的准确性。本文根据曲线位置将该图划分为两部分,曲线下方的面积被称为AUC(area under curve),AUC值越高,曲线越接近左上角(即X越小,Y越大),说明预测准确率越高,如图3所示。
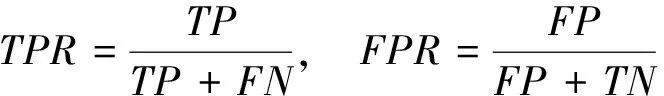
(5)
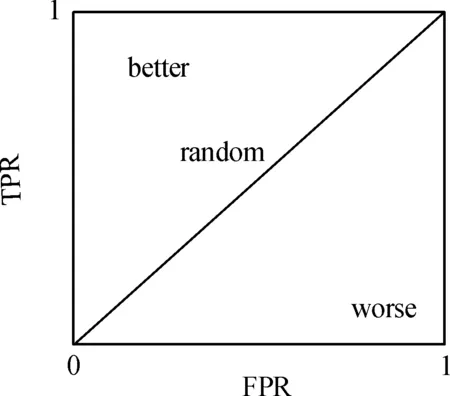
图3 ROC曲线评价示意图
2.2.3高桥隧比路段交通事故的重要性分析
高桥隧比路段交通事故的重要性分析是一种权重分析方法,用于描述某一因素或指标对研究目标的整体影响,更强调因素或指标间的相对重要性。本文所用的BP-Garson组合算法,是将每个隐含层神经元的“隐含层-输出层”连接权值分配到与其相连输入信号的连接权值上,依据式(6),确定了每个输入值对输出值的贡献量。
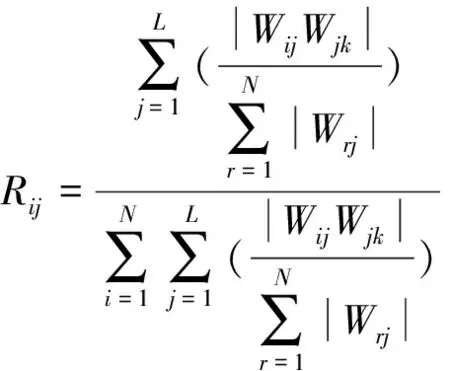
(6)
式中:Rij为输入信号相对重要性;Wij、Wjk分别为输入层-隐含层、隐含层-输出层间连接权值;i=1,2,…,N;k=1,2,…,M(N、M分别为输入信号、输出信号个数)。
3 模型建立
3.1 基于R语言的数据处理
建立的预测模型采用编码加函数调用的形式完成,所调用的函数资源见表3。

表3 神经网络调用的函数资源包
首先调用matrixPlot函数分析交通事故原始数据集,结果如图4示,灰度由浅到深表示数值从小到大,红色部分表示缺失数据。然后进行数据清洗,根据相关处理缺失数据理论[16],剔除掉不完整的129项数据,占数据集总量的4.8%。最后将预处理的数据集整理保存,其参数内容如表4所示。

图4 R语言预处理的交通事故数据矩阵图
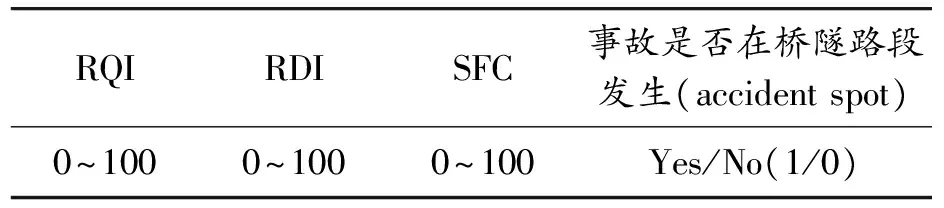
表4 神经网络建模的输入输出参数
3.2 预测模型的建立
3.2.1建立模型的归一化处理
将按路段划分的20段事故数据中2 707组有效输出参数及预处理输入参数进行归一化处理,结果如表5所示。
3.2.2BP-Garson算法的预测模型建立
“路面性能—桥隧段发生事故”样本的训练模型采用输入层、隐含层和输出层3层结构。将采集的RQI、SFC和RDI相关数据作为事故路段的路面性能输入参数,以交通事故发生地点是否位于桥隧段作为输出参数,构建二值分类的高桥隧比路段交通事故预测模型。调用函数包“Neuralnet”,参考相关文献[8,17],依据式(7)判断隐含层神经元训练个数范围在2~12,预测模型的训练结果以8个隐含层神经元为例,如图5所示。
(7)
其中:k为隐含层神经元个数;m为输入端参数个数;n为输出端参数个数;a=0~10。

表5 节选自2015年事故处理数据
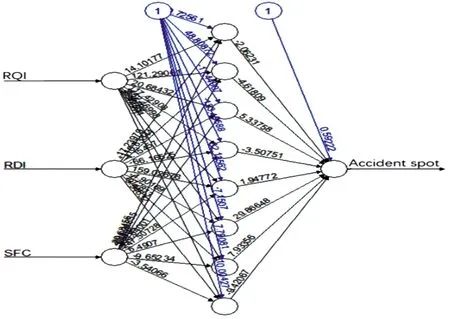
图5 “路面性能—桥隧段事故发生”的预测模型示意图(8个隐含层神经元)
设置随机数种子Seed,训练预测模型得出的结果如表6示。可以发现,不同个数的隐含层神经元所构建的二值分类预测模型存在差异,这是神经网络算法本身网络结构所决定的。针对训练模型存在的波动性差异,本文利用k=3、5、8这3组预测模型对比分析高桥隧比路段交通事故的发生规律。从2014—2016年的“路面性能—桥隧段发生事故”样本中随机抽样得出70%的数据,通过训练建立预测模型,把剩余的30%事故数据用于模型拟合效果的评价。
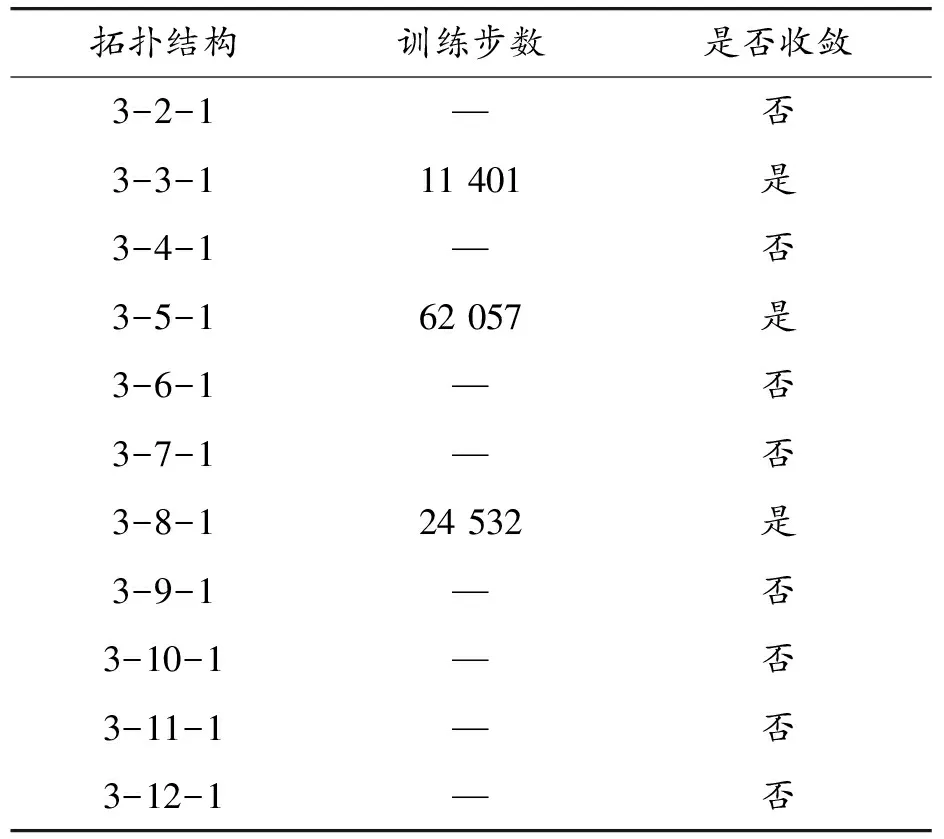
表6 桥隧段发生交通事故预测模型的训练结果
4 预测模型的评价
4.1 预测模型的受试者工作特征曲线
不同隐含层神经元训练的ROC曲线均位于random曲线的左上方,这意味着所建立的预测模型具备可靠性[18]。如图6所示,隐含层神经元个数为8的ROC曲线位于最左上方,说明模型的预测精度较其他曲线最大。此外,预测模型的拟合效果随隐含层神经元个数的增多而提高,表明网络结构复杂化有利于提高模型精度。
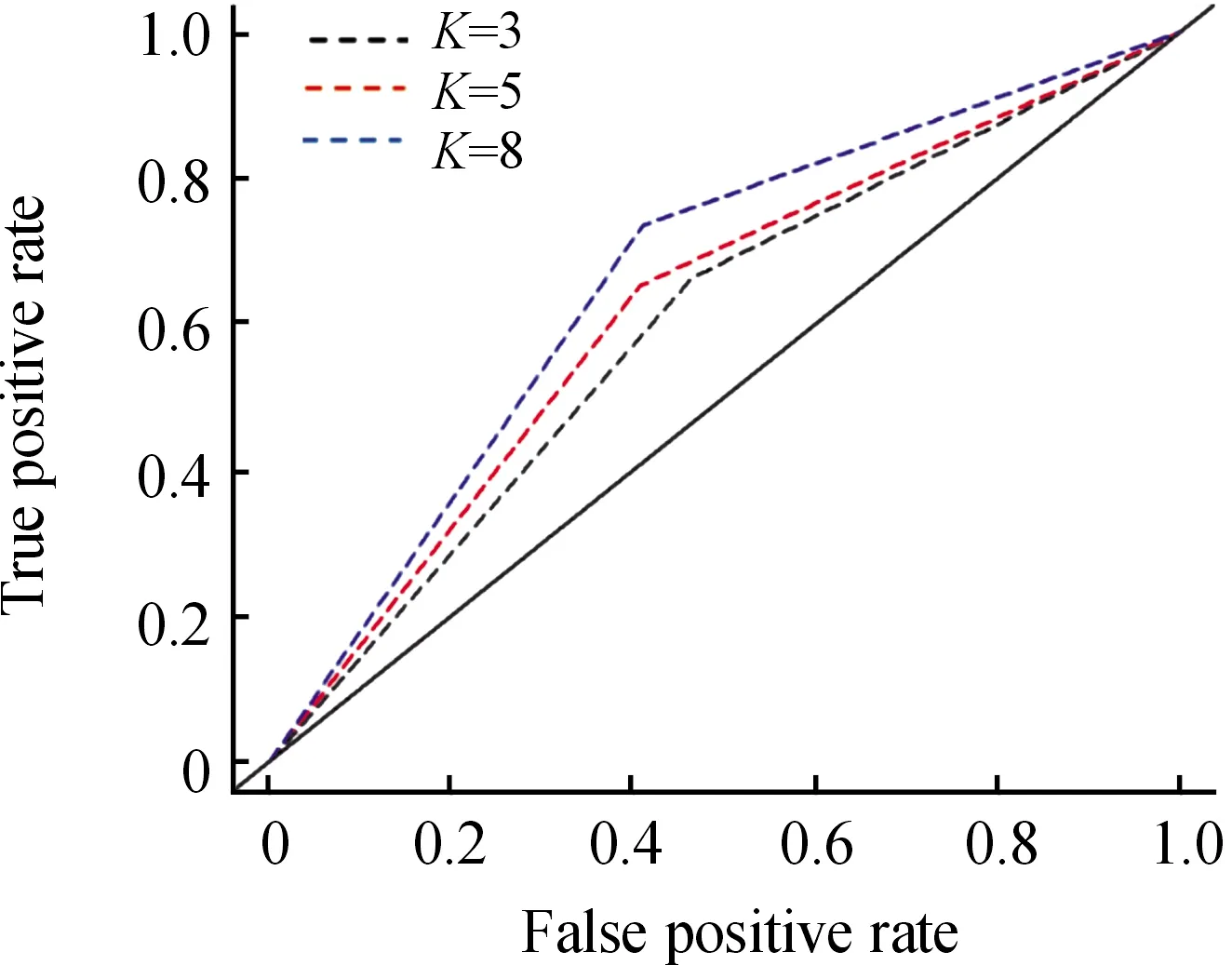
图6 “路面性能—桥隧段事故发生”的ROC曲线
4.2 模型的准确度对比
依据混淆矩阵分析高桥隧比路段2014—2016年的交通事故发生率,结果如表7所示。预测模型的训练结果ACC为0.6~0.7,代表该模型拟合效果好[16]。为了进一步量化预测模型拟合效果,采用精确度及样本召回率对其分析。隐含层神经元个数为8时的预测精度最高,可达0.612;神经元个数为5时的样本召回率最高,为0.593。神经元个数为8时的预测模型能防止结果过拟合,并兼顾结果的准确度,能更好地满足预测要求。从实际预测值来看,该模型在30%测试样本下的预测事故率也逼近了所对照的样本事故率。

表7 BP预测模型的拟合效果
4.3 重要性分析
传统BP神经网络预测模型仅能依据黑箱算法给出预测的输出值,而BP-Garson组合模型能对训练模型各因素的组成贡献进行分析。本研究调用R语言的“NeuralNetTools”包的Garson算法编写分析代码,将预测模型各参数的重要性对比结果进行可视化分析。为保证预测结果具有典型性,分别对不同隐含层神经元建立的预测模型进行模型参数的重要性分析,结果如图7所示,k值代表不同隐含层神经元的个数。3种性能参数的重要性排序结果表明,SFC是影响高桥隧比路段交通事故发生率的主要影响因素,RQI和RDI为次要因素。
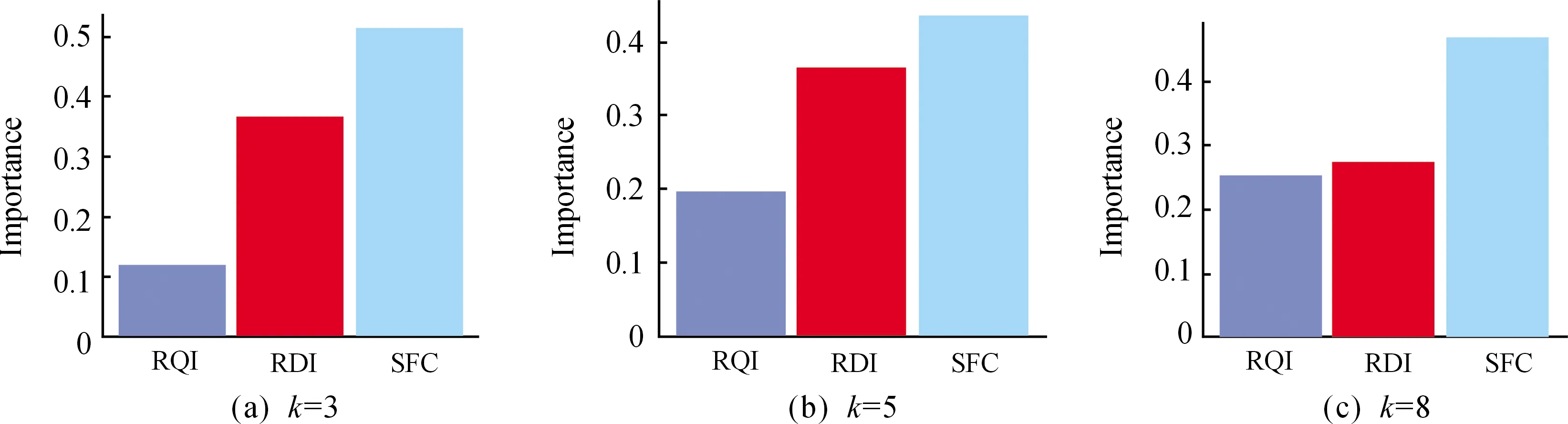
图7 路表性能各指标占预测模型的重要性分析结果
5 结论
1) 二值分类预测模型的拟合效果较好。对3年间近3 000组的交通事故数据进行训练建模,所建立的BP-Garson预测模型ACC最高可达0.674,具有较好的拟合效果,分析ROC曲线发现,当隐含层神经元个数为3、5和8时,预测模型的AUC面积均大于random曲线。
2) 模型的预测结果精确度高。预测模型的精确度随隐含层神经元的个数增加而提高,当神经元个数为8时,预测精确度高达61.2%,样本召回率为59.0%。研究发现在SFC、RQI、RDI这3种路面性能参数中,SFC值是高桥隧比路段交通事故发生的主要影响因素。
3) 基于二值分类系统预测交通事故影响因素的方法具备可行性。依据路面路表性能可以较好地判断出该高桥隧比路段的事故发生率,在样本事故率为41.6%时,8个神经元模型预测的事故发生率达40.0%。
4) BP-Garson预测模型可用于山区高速交通事故率的预测研究。预测模型的拟合效果和重要性分析的结果均表明,仅依靠收集路面路表性能就可在一定误差范围内预测同一路段的事故发生率。

