基于局部特征的二维白化重构

田甲略，朱玉莲，陈飞玥，刘佳慧

（1. 南京航空航天大学计算机科学与技术学院/人工智能学院，南京 211106；2. 南京航空航天大学公共实验教学部，南京 211106）

引言

白化作为一种数据预处理方法，由于可以在标准化数据的同时去除输入数据各属性间的相关性［1］，从而从计算和统计的角度简化多元数据分析的复杂度［2］，因此在图像处理［3］、语音处理［4］、三维物体识别［5］等方面得到广泛应用。

白化，就是一种将d维随机向量x经过白化矩阵W变换到新向量y的线性转换过程［2］（即y=Wx），其核心是寻找白化矩阵W，使得经过W变换后各属性间不相关且各属性的方差都相等。在各种白化方法中，PCA 白化（Principle component analysis）［6］和ZCA 白化（Zero-phase component analysis）［7］是两种最常见的方法。PCA 白化是在PCA［8］的基础上做了尺度上缩放，使得白化后各属性的方差为1。设协方差矩阵为Σ，且其奇异值分解为Σ=UΛUT，则PCA 的白化矩阵可表示为WPCA=Λ-1/2UT。PCA 白化可以使y能够尽可能多地表示原始x中的信息；而ZCA 白化则是将PCA 白化的结果经过U旋转回到原始空间的操作，其白化矩阵为WZCA=UΛ-1/2UT，因此ZCA 白化后的结果更接近原始数据。值得说明的是，由于PCA 白化和ZCA 白化均是在PCA 基础上进行的转换，因此在求解白化矩阵时通常需要使用整个已知数据集，并且该数据集中的所有样本均共享一个白化矩阵W。

白化在图像处理方面有着广泛的应用，例如，文献［3］使用ZCA 白化去除车牌图像邻域像素间的冗余信息；文献［9］使用ZCA 白化作为深度神经网络输入前的预处理步骤；文献［10］则说明了白化操作有助于提高传统机器学习算法对光照、噪声等鲁棒性。Shi 等［11］提出了一种二维白化重构（Two-dimensional whitening reconstruction，TWR）算法。作为一种图像预处理方法，不同于PCA 白化和ZCA 白化方法，TWR 白化矩阵的求解只依赖于要进行白化的单张图像而不需要使用其他图像。也就是说，每个图像在进行TWR 白化变换时都对应各自专属的白化矩阵。文献［11］在人脸识别上的实验结果验证了经过TWR 处理后的图像能够有效提高PCA 及其变体算法的分类和聚类效果。

本文将阐述TWR 等价于基于列的ZCA 白化。亦即，对单张图像进行TWR 操作等价于以图像列向量作为样本所进行的ZCA 白化操作。由于ZCA 白化能有效去除随机变量各属性间的相关性，因此当把图像的每一列作为随机变量时，ZCA 白化就相当于去除图像列内各属性的相关性。考虑到图像局部块内的冗余信息要远大于列内的冗余信息，基于上述等价性的发现，提出了重组的TWR（Reshaped TWR，RTWR）算法。RTWR 首先将图像进行重新组合，使得重组后矩阵的每一列对应着原始图像的一个局部分块。随后基于这个重组后的矩阵做TWR 操作以期去除图像局部块内的相关性。

另一方面，由于在图像处理中局部信息相对于全局信息而言对光照变换、目标遮挡等具有更好的鲁棒性［12-13］，因此有效获取局部特征成为必要。子图像方法［14-15］是一种非常有效的获取图像局部特征的方法。该方法通过对原始图像进行划分，然后分别在每个子图像中提取特征来获取局部特征。鉴于子图像方法的成功，从局部的角度出发，提出了基于块的TWR（Patch TWR，PTWR）算法。不同于RTWR 对图像重组后做TWR，PTWR 对每个分块分别进行TWR，然后把每块的TWR 结果按位置拼接成新的矩阵，最后再对新的矩阵进行降维或分类。为了验证RTWR 和PTWR 算法的有效性，在ORL、CMU PIE 和AR 人脸数据集上进行实验。实验结果表明RTWR 和PTWR 均优于TWR，尤其是PTWR 算法，对人脸尺度变换、角度变换、光照及遮挡变换均具有非常好的鲁棒性，并且在训练样本较少的情况下这种优势更为突出。此外，对PTWR 算法中的参数选择进行了分析。

1 TWR 与ZCA 白化的等价性

1.1 二维白化重构算法

TWR［11］是针对单张图像进行的白化方法。它对图像进行白化的同时还可以使图像的像素分布接近高斯分布［11］。文献［11］的实验结果表明，图片经过TWR 预处理后再进行PCA 及其变体算法的降维操作能够显著提升后续的分类和聚类效果，并且对光照变换具有较强的鲁棒性。

给定一张p行n列的图像X=[x1，x2，…，xn]∈Rp×n，其中，xi(i=1，2，…，n)是图像X的列向量。TWR 首先将图像的每一列看作一个处理单元进行列内的去均值化操作［16］，得到列内中心化后的图像X～=[x～1，x～2，…，x～n]，然后对X～进行奇异值分解［17］，即X～=UDVT，则图像X～经过TWR 后的结果可表示为

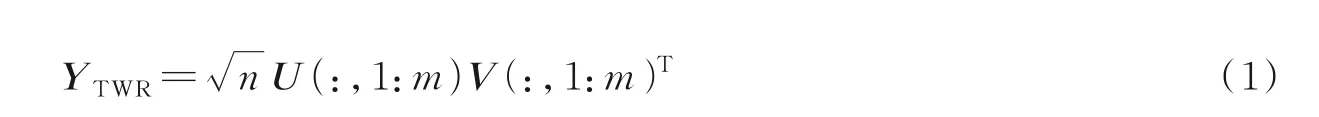
式中m表示要保留的主分量的个数。

1.2 TWR 和ZCA 白化的等价关系

本节将说明对图像的TWR 操作等价于基于图像列向量的ZCA 白化。

同1.1 节，给定图像X，经过列中心化处理后得到的图像表示为X～=[x～1，x～2，…，x～n]∈Rp×n，其奇异值分解为

由式（1）和式（5）可得：YZCA=YTWR。因此，TWR 等价于将图像的每一列作为一个样本进行ZCA白化。

2 RTWR 和PTWR

2.1 RTWR

根据1.2 节的结论可知，对图像X整体进行TWR 预处理等价于将图像X的每一列作为一个样本进行ZCA 白化的操作，这就是说TWR 能有效去除图像列内的相关性。因为图像结构信息的存在，局部块内的冗余信息要远多于列内的冗余信息，因此从去除冗余信息的角度出发，提出了RTWR 方法。RTWR 首先对人脸图像进行重新组合，使得重组后的矩阵的每一列对应着原始图像的一个局部块，然后针对新的重组矩阵进行TWR 操作，最后将每一列还原成局部块，并对所有块进行重组。具体的实现步骤如下：

（5）分别将Y中每一列yk(k∈{1，2，…，n～})重组为a×b大小的块，并将它们按原始块位置重新组成p×n大小的矩阵，得到RTWR 的结果（图1（d））。

图1 RTWR 具体操作流程(图像来自CMU PIE)Fig.1 Operation process of RTWR (images from CMU PIE)

值得说明的是：①当分块大小和原始图像大小一致时，经过步骤1 和2，整个图像会重组成一个列向量，即Xnew为列向量；由于步骤3 中所获得的X～new只是对Xnew列内元素进行了去均值的处理，仍为列向量，因此步骤4 对Xnew白化处理后结果是不变的，即Y=Xnew，所以当Y还原为原始图像大小的图像后该重构图像和原图像只是差了一个均值。也就是说，当分块大小和原始图像大小一致时，RTWR 只是对图像元素做了一个去均值的处理。②当每个分块对应原图像的每一列时，步骤2 的重组操作并不会改变原始图像的结构，即Xnew=X。因此当对Xnew做TWR 时就等同于对X做TWR，所以，当图像的每个分块对应于原图像的每一列时，RTWR 退化为TWR，也就是说TWR 是RTWR 的一个特例。

2.2 PTWR

RTWR 方法通过将图像的每个子块拉成列向量实现对原始图像的重组，然而这样的操作在一定程度上会破坏图像的局部信息。为了充分利用图像的局部信息，同时鉴于子图像方法在图像去噪、小目标检测［18］等研究领域的成功应用，提出了PTWR 算法。不同于RTWR 将图像分块拉成列向量拼接后整体进行TWR 操作，PTWR 是在每个子块内分别做TWR，以期保留更多的局部信息。

PTWR 的具体流程如下：给定一张图像X∈Rp×n，首先不重叠地将图像分成若干个大小a×b的矩形块Xij(i∈{1，2，…，p/a}，j∈{1，2，…，n/b})；然后在每个分块上分别进行TWR 操作，最后将每块的处理结果复位重新构成大小为p×n的矩阵，该矩阵即为X经过PTWR 后的结果。图2 展示了图像经过PTWR 的处理过程。在图2（a）中，16×16 大小的人脸图像被划分成16 个4×4 的矩形块，然后每个4×4 的块分别做TWR 操作（图2（c）），最后所有TWR 处理后的块按位重组成16×16 的矩阵（图2（d））。值得说明的是，当把整张图像看作一个分块时，此时PTWR 就退化为TWR。也就是说，TWR 也是PTWR 的一个特例。

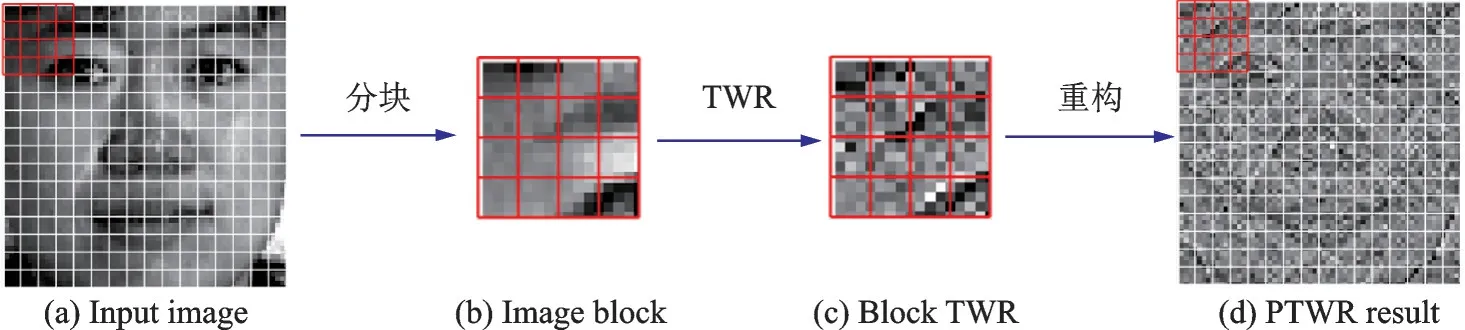
图2 PTWR 具体操作流程Fig.2 Operation process of PTWR

图3 分别给出了原始图像和经过RTWR 与PTWR 处理后像素点的分布情况。从图中可以看出，严重受光线影响的图像其像素点的分布主要集中在低值区域（图3（a））；但图像经过RTWR 处理后（图3（b）），像素分布接近高斯分布；而图像经过PTWR 处理后（图3（c）），像素分布更趋于平均化。因此，经过RTWR 和PTWR 预处理的图像，其像素分布更接近高斯分布或均匀分布。

图3 像素分布对比Fig.3 Comparison of pixel distribution

图4 给出了一组图像分别经过3 种预处理后结果。从图4 可以很明显地看出，RTWR（a×b=8×4，m=28）和PTWR（a×b=8×4，m=2）预处理后的图像轮廓比TWR 更清晰，同时结构化特征也更突出。

图4 TWR、RTWR 和PTWR 处理效果对比(图片来自ORL)Fig.4 Processing results of TWR, RTWR and PTWR (images from ORL)

3 实验结果与分析

为了验证RTWR 和PTWR 方法的有效性，本文在ORL、CMU PIE 和AR 人脸数据集上对RTWR、PTWR 和TWR 进行对比实验。其中，ORL 数据集主要用于测试算法对人脸轻微角度旋转、图像尺度缩放的鲁棒性；CMU PIE 数据集主要用于测试算法对光照变换的鲁棒性；而AR 数据集则是用于测试算法对各种面部遮挡的鲁棒性。另外，还分析了算法中图像分块大小a×b及主分量的个数（m）对算法性能的影响。

3.1 数据集

（1）ORL 人脸数据集［19］

ORL 人脸数据集包括40 个人的共400 张图像（每人10 张图像），这些图像包含人脸转动角度的变换（不超过20°）、面部表情和配饰（眼镜等）的变换以及图像尺度的变换（放缩比例约为1.2）。原始图像大小为112×92，本文在使用时将其缩放为32×32 大小。

（2）CMU PIE 人脸数据集

CMU PIE 人脸数据集包括68 个人在13 种姿势变换、43 种光照变换以及4 种表情变换下的41 368张图像。本文中所使用的图像为文献［20］处理后的子集（C27）。该子集共包括3 329 张正面图像，每类人脸有49 张图像（除第38 类是46 张图像），每张图像大小为64×64。

（3）AR 人脸数据集［21］

AR 数据集包含126 个人（70 个男性和56 个女性）的4 000 余张包括不同的表情、光照和遮挡变换的彩色人脸正面照。本文中，选用其中的一个黑白图像子集，该子集包括100 个人（50 个男性和50 个女性，每人26 张）的2 600 张图像，每张图像大小为64×48。每人的26 张图像分别在两个场景拍摄得到，且每个场景有13 张图像。对于每个场景的13 张图像而言，1st 为中立图像、2nd～4th 为表情变换图像、5th～7th 张为光照变换图像、8th～10th 张为眼部遮挡图像（眼镜），而11th～13th 张为嘴部遮挡图像（围巾），如图5 所示。

图5 AR 数据库样例Fig.5 AR database samples

3.2 实验设置与结果

在实验中，首先分别使用RTWR、PTWR 和TWR 三种方法对每张图像进行预处理，然后使用PCA或2DPCA［22］对处理后的结果进行降维，最后使用最近邻分类器进行分类（欧式距离），并将分类结果作为分析的依据。现对实验设置进行说明。对于ORL 数据集，从每类图像中随机选取q(q=2，4，6，8)个样本组成训练集，其余样本用于测试。在实验中，TWR 采用与文献［11］相同的参数设置，即m取28；RTWR 和PTWR 的图像分块大小均为8×4，m分别取28 和2。实验重复20 次，最后给出平均识别率。对于CMU PIE 数据库，从每类图像中随机选取q(q=2，4，6，8)个样本组成训练集，其余样本用于测试。TWR 的m取40；RTWR 和PTWR 图像分块大小为分别为32×2 和16×4，m分别取40 和2。实验重复20 次，最后给出平均识别率和标准差。而对于AR 数据库，每类图像第一个场景的前7 张（表情和光照变换）图像组成训练集，两个不同场景下的眼部遮挡和嘴部遮挡分成4 个测试集分别用于测试。在TWR 中，m=44；RTWR 和PTWR 的图像分块大小取12×6，m分别取44 和5。

图6 和表1、2 分别给出了ORL、CMU PIE 和AR 数据集经过TWR、RTWR 和PTWR 预处理后进行PCA 和2DPCA 降维后的分类结果。从整体的结果上可以看出，RTWR 和PTWR 均优于TWR。具体而言：（1）对于有轻微角度变换和尺度变换的ORL 数据集，RTWR 比TWR 表现稍差，而PTWR 则明显优于TWR，尤其是当训练样本较少时（如q=2 或4 时），这种优势更为明显。（2）对于包含各种光线变换的CMU PIE 数据集，RTWR 并没有获得比TWR 更好的性能。在使用PCA 进行降维时RTWR 略优于TWR，而使用2DPCA 时RTWR 表现略差于TWR，整体上两者性能相当；而PTWR 却给出相当令人满意的结果。当训练样本数为2，使用2DPCA 降维时，PTWR 比TWR 能高出5.7%；同时，PTWR 有比TWR 更低的方差，这也说明PTWR 比TWR 更具有稳定性。（3）对于有眼部遮挡和嘴部遮挡的AR 数据集，RTWR 和PTWR 均明显比TWR 具有更好的性能。相对于TWR 而言，RTWR 和PTWR 最小的提升幅度分别为3.0%和0.7%；而最大的提升幅度则为6.0%和12.4%；（4）比较表2 中RTWR 与PTWR的实验结果发现，RTWR 在处理眼部遮挡时比PTWR 更具有优势，而PTWR 则对嘴部遮挡等影响因素表现出很好的适应性。

表1 CMU PIE 数据集实验结果Table 1 Experimental results on CMU PIE%

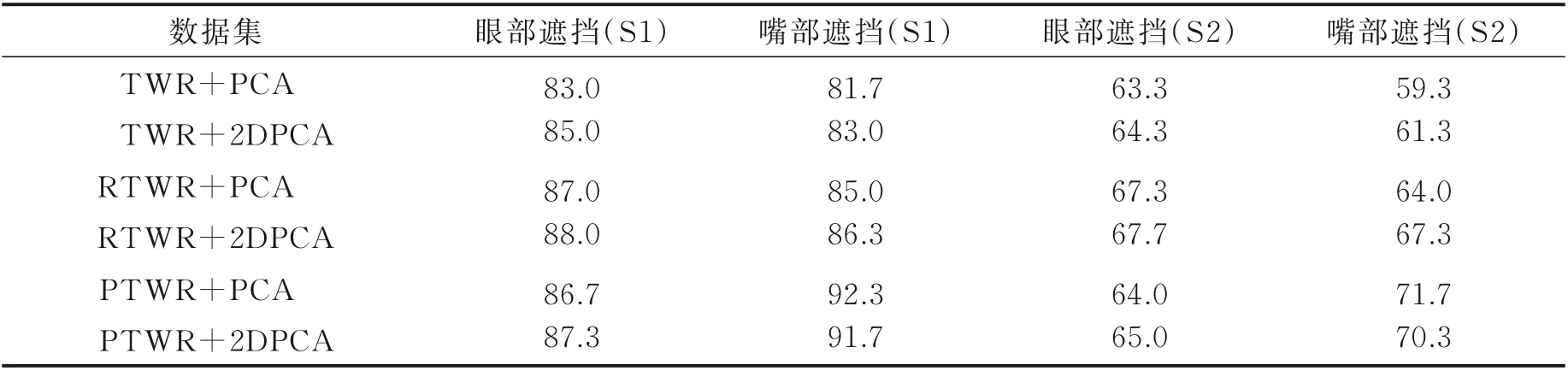
表2 AR 数据集实验结果Table 2 Experimental results on AR%

图6 ORL 数据集实验结果Fig.6 Experimental results on ORL dataset

3.3 参数分析

3.3.1 块大小对性能的影响

在RTWR 和PTWR 方法中，块大小（a×b）是一个非常重要参数。图7 给出了采用不同块大小（a=b）时RTWR 和PTWR 预处理后的结果。从图7 可以看出：（1）对于RTWR，无论采用怎样的分块大小都能清晰看出图像的轮廓。随着分块的增大，RTWR 重组后的轮廓不仅越来越清晰而且也越来越接近于原始图像。2.1 节的分析表明，当a=32 时（此时分块大小与原图像相同），RTWR 重组的图像和原图像只相差一个灰度差；（2）对于PTWR，当分块大小较小时（如a=2），很难看出图像的轮廓；而随着a的增加，图像轮廓逐渐清晰。当a=32 时（此时分块大小于原图像相同），PTWR 退化为TWR，此时轮廓最为清晰。关于RTWR 重构结果和PTWR 的差别，可以做如下分析：RTWR 是以去除局部块内相关性的角度出发，首先将图像进行了重组（使得重组后的每一列对应着原始图像的一个局部块）然后TWR 直接执行在重组的图像上。虽然RTWR 将图像进行了划分，但由于TWR 是作用在整体重组图像上的，因此RTWR 相对更侧重于获取图像整体信息，因此，图7（a）中人脸轮廓清晰可见；而PTWR 则是从保持原始图像局部特征的角度出发，分别对每个分块做TWR 操作，然后通过TWR 获取每个分块的信息。因此PTWR 更侧重获取图像的局部信息。所以图7（b）中所呈现的PTWR 重构后图像相邻区域间变换较大（分块为2×2 时尤为突出）。鉴于RTWR 与PTWR 的上述差别，进一步分析了分块大小对两种方法性能的影响。

图7 不同分块的白化效果图Fig.7 Renderings of different blocks

（1）分块大小对RTWR 的影响

在RTWR 方法中，TWR 保留主分量的个数（m值）的选取与分块大小密切相关。对一张p×n大小的图像以a×b大小进行分块重组将得到大小为p～×n～(n～=p*n/p～，p～=a*b)的图像，那么m取值一定需要满足1 ≤m≤min(n～，p～)。而太大或太小的分块都会导致n～或p～很小，从而使得m最大取值很小，进而影响RTWR 最后的性能。本文尽量保证选取的主成分的个数能与TWR 方法一致，因此遵循分块重组后图像尺寸尽可能接近原始图像尺寸的原则对图像进行分块。如对于64×64 的原始图像，采用32×2 的分块，以使得重构后的图像仍然是64×64。然而重组成64×64 的图像会存在多种分块情况（如4×16，16×4 等），仍然无法选择采用哪种分块形式。鉴于集成学习方法往往能够弱化各个分类器的不足，对提高最终分类器的性能有着较好的适用性［23-24］，因此考虑采用集成的方法设计多分类器系统。即每种分块情况分别设计一个子分类器，最终将所有子分类器的结果进行简单的投票。在CMU PIE数据集上进行相关实验。实验中，从每类图像中随机选取q(q=2，4，6，8)个样本用于训练，剩余的样本组成测试集。针对每组训练样本和测试样本，首先将图像按块a×b进行分块重组处理（如2.1 节步骤1，2），然后对重组的图像进行RTWR 操作（同TWR 取相同的m，即m=40），最后使用PCA 降维并用最近邻分类器进行分类。针对于每一种分块(a×b=1×64，2×32，4×16，8×8，16×4，32×2，64×1）均做上述处理，因此对于每个测试样本均能获得多个分类结果，最后将所有分类结果进行投票，并将此投票结果作为该测试样本的类别。重复实验20 次取平均识别率。

实验结果如表3 所示。从表3 可以看出，①分块大小对RTWR 的影响的确很大：当分块为1×64时识别效果最差，而在32×2 时效果最好，两者最大相差6%；②集成分类器所得结果与单一分块相比在识别率和稳定性方面均表现良好，集成后的结果仅次于所有分块中的最优性能且总体上相差并不大（最大差距不到1%，最小差距只有0.1%）。因此在确定重构图像大小的前提下，采用这种集成方式来弱化具体分块选择是可行的。

（2）分块大小对PTWR 的影响

PTWR 方法首先将图像进行分块，然后分别对每块做TWR 处理，因此PTWR 属于子图像方法［15］。对于子图像方法，分块大小是一个非常重要的参数，它严重影响着最后的性能。本文将讨论分块大小对PTWR 的影响。分块大小不宜过小或过大，过小的分块会导致过多的考虑局部信息而忽略全局信息的重要性，从而可能会造成全局信息的丢失；而过大的分块则会忽略局部信息的重要性。为简单起见，仅考虑正方形分块的情形，即a=b。在CMU PIE 数据集上进行相关实验。实验中，从每类图像中随机选取q(q=2，4，6，8)个样本用于训练，剩余的样本组成测试集。针对每组训练样本和测试样本，首先将图像按块a×a(a=2，4，8，16，32，64)进行分块处理，然后对分块后的图像进行PTWR 操作（对应分块情况下的m分别为1，2，4，12，28，40），最后使用PCA 降维并分类。重复实验20 次取平均识别率作为最后的结果。

图8 展示了在CMU PIE 数据集上分块大小对PTWR 识别效果的影响。从实验结果中可以看出：①当分块大小为8×8（最接近原图像大小的1/100）时PTWR 取得了最好的识别效果，这也验证了文献［25-26］的经验结论，即子图像大小在原图像大小的1/100 附近时，子图像方法往往能够获取较好效果。②整体上说，当分块大小为2×2 时识别率较低，随着分块大小的增加，识别性能逐渐增加；当分块为8×8 时达到最好的效果；而后随着分块的增加识别率又逐渐减低。值得说明的是，虽然PTWR 的分块对性能有较大影响，但从整体上来看，PTWR 在大多数分块情况下，性能都优于TWR。③在每类训练样本较小时（q=2），PTWR 算法对应的实线和TWR 算法对应的虚线所夹面积相差较大；而随着训练样本数的增加，所夹面积逐渐变小，这也说明了训练样本较少的情况下PTWR 算法相对于TWR更具有优势。值得说明的是，当分块大小和原始图像大小一致时，PTWR 就转换为TWR，即TWR 为PTWR 的一个特例。

图8 分块大小对PTWR 的影响(CMU PIE)Fig.8 Effect of patch size on PTWR (CMU PIE)

3.3.2 主分量个数（m）对性能的影响

（1）主分量个数对RTWR 的影响

从表3 的数据可以看出，集成学习能够有效弱化分块大小对RTWR 识别率的影响，进而解决分块大小难以选择的问题。本节将在集成分块的基础上，讨论m值对RTWR 的影响。以CMU PIE 数据集为例，以RTWR 重组后的图像大小和原图像相同为分块原则，考察了m值从4 开始以4 为步长变化至64 对集成RTWR（所有可能分块的集成）的影响。图9（a）给出了m对集成RTWR 和TWR 两种方法的性能影响，其中q表示每类有q个样本做训练，其他样本做测试。从图9 可以看出：①随着m的增加，两种方法的识别率都是先上升然后逐渐趋于平稳再下降的走势。这主要是因为当m较小时只有很少的有用信息被使用，而大量的有用信息丢失，所以性能较低；反之，当m较大时，一些噪声信息将会被利用，从而导致识别性能降低。②随着训练样本数目q的增加，m对集成的RTWR 和TWR 的影响逐渐减小，尤其是对集成的RTWR 影响更小。图9（a）显示，除q=2 外，两种方法的m在块尺寸的50%～80%之间时均取得较好的识别率。

表3 CMU PIE 数据集RTWR 分块大小实验结果Table 3 Experimental results of patch size analysis of RTWR on CMU PIE%

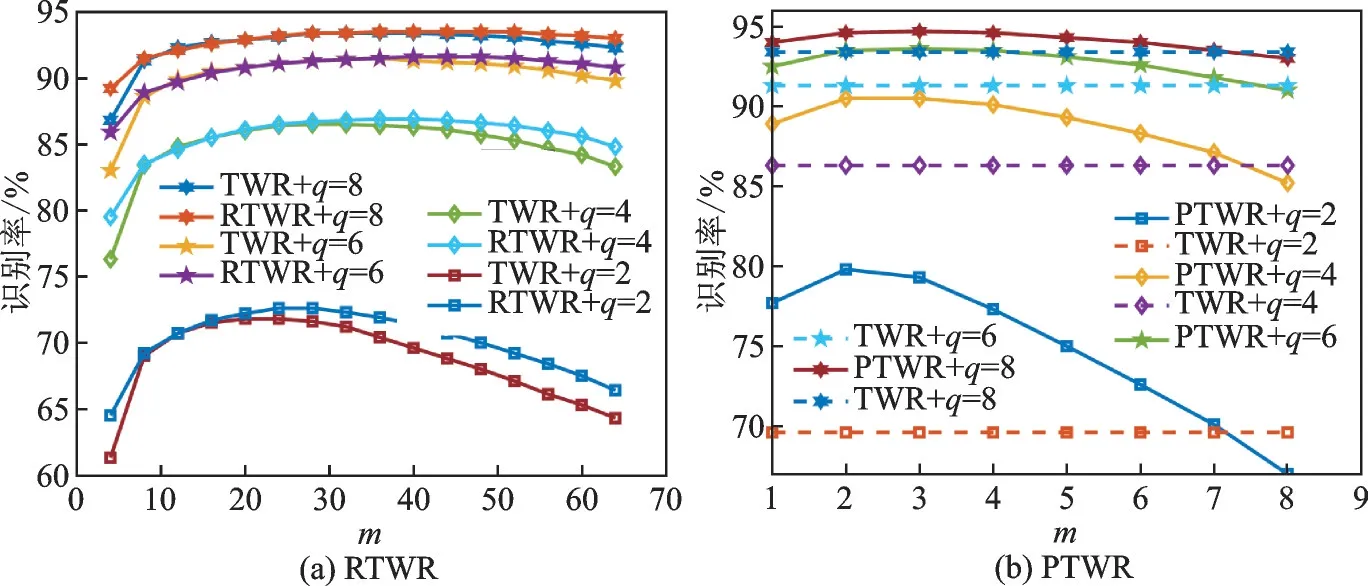
图9 参数m 对识别率的影响(CMU PIE)Fig.9 Effect of parameter m on recognition rate (CMU PIE)

（2）主分量个数对PTWR 的影响

图8 的实验结果显示，在CMU PIE 数据集上，当分块大小为8×8 时PTWR 获得了最好的识别性能，因此，将在8×8 的分块情况下考察m对PTWR 识别效果的影响。实验仍然以CMU PIE 为例，主分量个数m从1 开始变化至8（对于8×8 的分块，最大的m为8），得到不同m值对应的PTWR 的识别结果。为了进行性能比较，在图9（b）中也给出了TWR 在m=40 时的性能。从实验结果可以看出，当每块保留主成分信息过少时（m=1），因为大量的信息被丢弃，所以对应的识别效果并不理想；而当保留所有主成分信息时（m=8），由于可能使用了包含随机噪声在内的信息，从而影响了后续的分类操作。在8×8 的分块情况下，m=2 时达到最优的识别效果，并且在几乎所有取值下（除m=8）PTWR 均获得了比TWR 更好的性能。

4 结束语

本文首先证明了基于单张图像的TWR 预处理与对单张图像按列做ZCA 白化操作的等价性关系；然后在两者等价性的基础上，从去除图像局部块内相关性的角度提出了基于重组的RTWR 算法；从尽可能提取原始图像结构信息和局部特征的角度，提出了基于块的PTWR 算法。在ORL、CMU PIE 和AR 数据集上做了对比实验，实验结果表明，本文提出的RTWR 和PTWR 相对于TWR 对表情、光照、遮挡等影响因素具有更好的鲁棒性。另外，还讨论了子块大小以及主成分个数对算法性能的影响。