基于图像插值的小样本手写数字识别研究

宋 伟，谢建平，高 倩，谢良旭，4，许晓军，4

（1. 江苏理工学院电气信息工程学院，常州 213001；2. 湖州师范学院理学院，湖州 313000；3. 江苏理工学院计算机工程学院，常州 213001；4.江苏理工学院生物信息与医药工程研究所，常州 213001）

引言

人工智能探索让计算机以类人脑方式学习和认知。随着超大容量计算机存储的普及和互联网对人类活动的时空突破，涌现出了大量可用数据。快速且高度并行的计算机硬件结合大数据推动了人工智能的发展，特别是引发了深度学习在诸多领域的技术革命［1-3］。需要指出的是，人工智能的高成效通常需要有充足的数据来训练模型参数，使其达到预测/识别的高精度和良好泛化能力。然而，在很多实际应用场景，样本数量不足或者样本标注存在较大困难而无法实现有效标注。高质量数据的缺乏往往使得人工智能算法极易出现过/欠拟合行为而很难达到预期成效。因此，小样本学习，即通过少量样本学习得到解决问题的方法就成为人工智能领域的重要研究方向之一。

小样本学习目前在图像目标识别、图像分割、图像分类与检索等诸多图像处理任务中都有重要应用［4-16］。例如，汪航等［13］使用2D Gabor 滤波增强图像，结合深度卷积自编码网络实现了小样本学习的合成孔径雷达（Synthetic aperture radar，SAR）图像识别。Gabor 滤波器能很好地把握图像的整体特征，同时还能够对其局部特征进行有效分析。最近，Li 等［16］发展了用于小样本图像分类的深度学习模型InterBoost。该模型首先构建两个相同框架的深度神经网络并随机初始化互补权重参数，然后通过互动式训练的方式进行两模型参数的联合迭代优化，其目的是得到两个具有独立特征提取的深度网络，最后取两个网络预测结果的平均值作为InterBoost 模型的最终输出。在多个小样品数据集上的测试结果表明，此方法相比于其他模型在图像分类识别精度上有显著提升。

手写文本是从古至今人类最为常用的交流和传播方式之一。在当今的数字化时代，海量的手写材料，如收据、支票、账单、邮件和手写试卷等需要录入计算机系统实现信息化处理。如何准确且快速地识别手写数字、字符及标记等有着广泛的商业需求和学术价值［17-22］。对于手写数字图像数据来说，由于个体书写习惯的多样性，书写力（笔压或笔力）、书写顺序、书写快慢以及连笔习惯等均存在个体差异，且具有一定的随机性，即同一个人在不同环境下的手写数字也不会完全相同，甚至有可能出现很大差异。因此，手写数字识别神经网络模型在数据缺乏时也很难取得应有的识别成效。如何在少量样本上进行模型训练从而实现对手写数字的精准识别有望为解决数据不足和样本不均衡提供有益的尝试。本文首先采用图像插值算法对手写数字图像进行预处理。不同于传统数据增强中增多数据的策略，本文着重于提高图像质量（分辨率），并在增强图像分辨率的基础上，详细研究两种常见神经网络在手写数字识别问题的数据集大小依赖性以及参数训练环节中迭代次数对小样本学习的影响。研究结果表明，图像插值预处理可以显著提升手写数字识别神经网络的特征提取质量，提高了模型的小样品学习性能。

1 材料和方法

1.1 小样本训练数据集和测试集

作为机器学习领域的一个经典数据集，MNIST 数据集包含60 000 张训练图像和10 000 张测试图像。所有图像均为28 像素×28 像素的灰度图像。为了研究手写数字识别神经网络模型的小样本学习性能并确保在小样本训练集中各数字的样本数一致，对于每个数字，从60 000 张MNIST 原始训练集中随机选取N个样本，合并组成大小为10×N个的训练数据集。通过改变N值，可以得到样本数可变的训练数据集，以此来验证神经网络在指定数目小样本上的手写数字识别的学习性能。对于不同的N值，本文统一使用同一个测试集，即10 000 张MNIST 测试集进行模型性能测试。

美国邮政服务USPS 数据集共有9 298 张尺寸为16 像素×16 像素的手写数字灰度图像。本文首先将USPS 整个数据集随机分成7 000 张训练图像和2 298 张测试图像。与MNIST 测试过程一致，对于每个数字，从7 000 张USPS 原始训练集中随机选取N个样本，合并组成大小为10×N个的训练数据集进行模型参数训练，并统一在2 298 张测试集中进行模型性能测试。

本文所使用的MNIST 和USPS 数据集均来源于Kaggle 在线平台（www.kaggle.com）。

1.2 图像插值

图像插值是图像预处理方法之一，常常应用于样本量不足时的图像增强以提高人工智能等算法的特征学习能力。图像插值通过利用已知像素产生未知像素的方法来引入不同的图像边缘效果，提高图像质量（分辨率）。根据产生未知像素色度值的方法不同，图像插值算法可分为最邻插值、双线性插值以及双三次插值等多种插值处理方式。

最邻插值（Nearest）是将原始图像的最近邻像素点的色度值直接赋值给插值后像素点的色度值。

双线性插值（Bilinear）利用原始图像中的4 个最近邻采样点的加权平均计算插值点的色度值，如图1 所示。图中，原始图像像素点（i，j），（i+1，j），（i，j+1）以及（i+1，j+1）为插值点（i+u，j+v）的4 个最近邻采样点。通过双线性插值公式

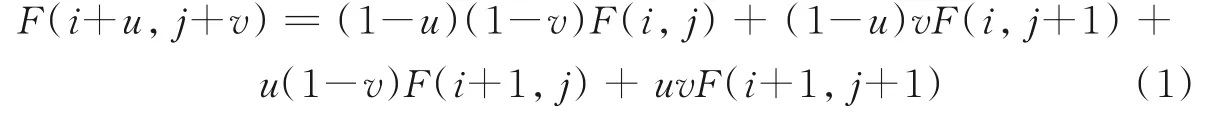
计算插值点（i+u，j+v）的色度值。其中：u、v为指定的内插值位置，F为对应点的色度值。

双三次插值（Bicubic）是一种更为复杂的插值算法，通过利用原始图像中16 个最近（包括最近邻和次近邻等）采样点的加权平均方式进行插值，从而引入相对平滑的图像边缘效果。

为了避免插值后的新图像发生形变，本工作对原始图像的高和宽维度均采用相同比例的插值放大，并使用缩放系数S=Hbilinear/Horiginal=Wbilinear/Woriginal表征。这里，（Horiginal，Woriginal）和（Hbilinear，Wbilinear）分别对应原始图像和插值后图像的高与宽的维度值。图1 给出了缩放系数S= 1.5 的MNIST图像双线性插值示例。插值后的图像为42 像素×42 像素的灰度图像。

图1 双线性插值算法Fig.1 Bilinear interpolation algorithm

1.3 神经网络

神经网络具有广泛应用性，尤其是随着计算机软硬件的提升，神经网络进入高速发展时期。针对本次研究的手写数字识别（分类）问题，分别选取全连神经网络和卷积神经网络作为学习器来验证基于图像插值的小样本手写数字识别研究。神经网络一般包含一个输入层、一个输出层以及若干个隐藏层。输入层神经元的数目需要与输入数据的维度匹配。图像插值处理后的图像尺寸会随着缩放系数S的改变而改变，因此，输入数据的维度由S值决定。对于手写数字识别模型，输出层为10 个神经元，其输出分别对应于0～9 数字的识别概率。

所测全连神经网络，如图2（a）所示，由两个全连接层（Dense layer）堆叠，其中第一个dense 层的输出神经元数（Units）为可调变量Xd。本工作通过改变Xd值来研究图像插值对全连神经网络的小样本学习性能的影响。图2（b）给出了所测卷积神经网络的模型架构。该模型在两层全连接层之前通过展平层（Flatten layer）堆叠一层二维卷积层（Conv2D layer），其输出过滤器数（Filters）为可调变量Xc。本文通过改变Xc值来研究图像插值对卷积神经网络的小样本学习性能的影响。

图2 测试模型Fig.2 Evaluated models

1.4 小样本学习的评价策略

神经网络的性能强烈依赖于训练数据的完整性，特别是在小样品学习中，由于数据缺乏，在小样品数据中学到的特征并不具有良好的泛化效果。因此，不同的小样本数据，同一模型在测试集上的测试精度存在一定程度的随机性，并且波动幅度通常随着训练数据集的减小而增大。为了尽可能地避免小样品数据的随机/波动性带来的误导，对于给定的各数字样本数N值，本文采用多次随机选取样本构建多个训练集（总样本数为10×N），并对每个训练集分别进行独立的模型参数训练，给出独立的测试精度。具体来说，重复次数M由N值决定，即

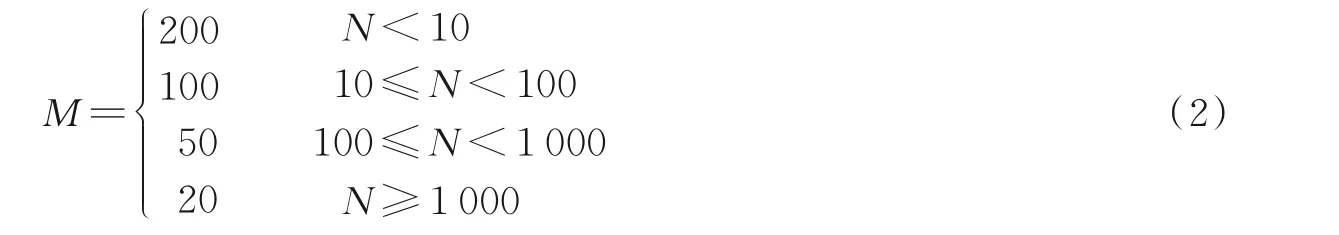
当使用完整训练集（60 000 张MNIST 图像或7 000 张USPS 图像）时，以N=6 000（MNIST）或700（USPS）标注，此时，M=1。M次独立训练及测试的平均测试精度评价样本数为N的神经网络性能。

针对手写数字图像分类问题，采用“RMSprop”和“categorical_crossentropy”分别作为优化器和损失函数进行模型参数训练。测试精度（Accuracy），即正确识别数目在测试集中的比例，是较为理想的模型性能评价指标。训练过程中的批量尺寸为min（N/3，128），即N/3 与128 的较小值。学习率固定为0.001（keras 默认设置）。另外，训练环节的迭代次数（Epoch）对神经网络的性能有较大影响。迭代次数太少（训练不够彻底），模型可能还处在欠拟合状态；反之，模型则极易出现过拟合现象。迭代次数的最优值与模型的学习效率及泛化能力有关。因此，本文还从迭代次数的角度研究图像插值对神经网络小样本学习性能的影响。

2 结果与讨论

2.1 实验环境

实验使用Ubuntu 18.04 操作系统，内存为32 GB，采用48 核的分布式计算机；计算环境需安装深度学习库Keras-2.2.2 和Tensorflow-1.3.0，数据的分析和存储使用Scikit-learn-0.19.2 和Numpy-1.18.1；使用Python-3.5.6 进行数据增加、模型训练和数据分析。

2.2 全连神经网络的小样本学习

图3（a）给出了迭代次数Epoch = 5，全连接层输出神经元数Xd分别为8、32、128、256 以及512 时的全连神经网络在MNIST 原始图像（未经插值处理）的测试结果。可以看出，全连网络从（原始）训练图像中学习到的特征在（原始）测试图像中的泛化能力随着Xd值的增大而提升，特别是在N较小时，提升效果显著。例如，当使用完整训练集（即N=6 000 时），Xd值的变化可引起测试精度从91.6%提高到98.2%。对于N=1 的超小样本学习，测试精度有28.3%的提升。当Xd≥256，且N≥128 时，不同N值的测试性能近乎重合，表明此网络架构在固定其他超参数的情况下达到了最优化模型容量（神经元数）。

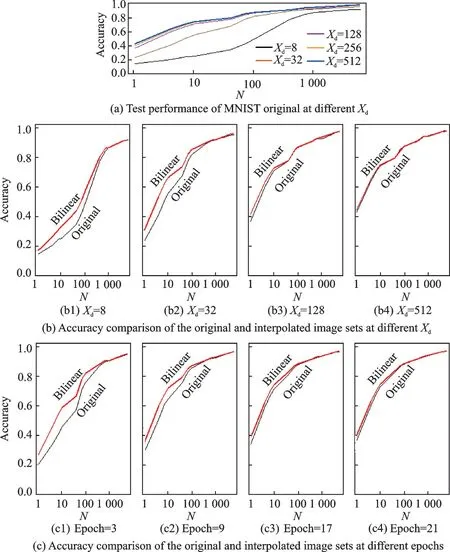
图3 全连神经网络Fig.3 Dense neural network

为直观给出双线性插值图像预处理对神经网络小样本学习性能的影响，图3（b）给出了迭代次数Epoch=5，Xd分别为8、32、128 以及512 时全连神经网络在MNIST 原始图像集（黑色线）和S= 1.5 的双线性插值图像集（红色线）的测试结果对比。可以看出，当N>1 000 或Xd趋近于最优化容量（=512）时，模型的测试精度与是否进行图像插值预处理近乎无关；而当N较小且Xd<128 时，图像在进行插值预处理后可以显著提升模型的小样本学习性能。例如，对于Xd=32，模型的测试精度增量最大可达12.3%。因此，双线性图像插值在小样本数据集中可以增加全连神经网络的特征提取能力，有助于提升模型泛化性。

图3（c）给出了神经元数Xd= 32，Epoch 分别为3、9、17 以及21 时全连神经网络在MNIST 原始图像集（黑色线）和S=1.5 的双线性插值图像集（红色线）的测试精度对比。可以看出，随着Epoch 值的增大，模型在大数据集（较大N值）中的表现与是否进行图像插值预处理近乎无关，表明了神经网络对数据量的依赖性。在较小N值（小样本学习）时，图像在进行插值预处理后可以提升模型的学习效率，即在同一Epoch 值时图像插值预处理有相对更佳的预测精度。Epoch 值越小，模型的提升效果往往越明显。例如，对于Epoch=3，模型的测试精度增量最大可达13.6%。双线性图像插值可以有效减少对训练集数据量和迭代次数的依赖。因此，双线性图像插值在小样本数据集中可以增加全连神经网络的特征提取能力，有助于提升模型的训练效率。

2.3 卷积神经网络的小样本学习

图4（a）给出了迭代次数Epoch=5，卷积层过滤器数Xc分别为4、8、32 以及128 时的卷积神经网络在MNIST 原始图像（未经插值处理）的测试结果。可以看出，卷积网络从（原始）训练图像中学习到的特征在（原始）测试图像中的泛化能力随着Xc值的增大而提升。特别是在N较小时，提升效果较为显著。例如，当使用完整训练集（即N=6 000 时），Xc值的变化可引起测试精度从97.7%提高到98.4%。而对于N=1 的超小样本学习，测试精度有7.1%的提升。

图4 卷积神经网络Fig.4 Convolutional neural network

图4（b）给出了迭代次数Epoch=5，Xc分别为4、8、32 以及128 时的卷积神经网络在MNIST 原始图像集（黑色线）和S=2.0 的双线性插值图像集（红色线）的测试结果对比。可以看出，对于较大样本数据集，模型的测试精度与是否进行图像插值预处理近乎无关。过滤器数Xc较小时，图像在进行插值预处理后可以提升模型的小样本学习性能。例如，对于Xc= 8，模型的测试精度增量最大可达5%。因此，双线性图像插值在小样本数据集中可以增加卷积神经网络的特征提取能力，有助于提升模型泛化性。需要指出的是，如图4（b3）和（b4）所示，图像预处理可引起测试精度稍许下降（即测试精度增量为负值），表明网络模型在当前的超参数下对于高分辨率图像数据存在一定程度的欠拟合。

图4（c）给出了过滤器数Xc=4，Epoch 分别为3、9、17 以及21 时的卷积神经网络在MNIST 原始图像集（黑色线）和S=2.0 的双线性插值图像集（红色线）的测试精度对比。可以看出，迭代次数Epoch 值较大时，模型的测试精度在不同样本数中的表现均与是否进行图像插值预处理近乎无关。与全连神经网络类似，在较小N值（即小样本学习）时，图像在进行插值预处理后可以提升模型的学习效率。例如，对于Epoch=3，模型的测试精度增量最大可达4.8%。因此，双线性图像插值在小样本数据集中可以增加卷积神经网络的特征提取能力，有助于提升模型的训练效率。

2.4 缩放系数对小样本学习的影响

缩放系数可以改变插值后图像的分辨率。分辨率不同，神经网络从相应训练数据集中学到的特征会有差异，从而改变模型在测试数据集上的测试精度。表1 列出了Epoch=5 时双线性插值不同缩放系数对全连神经网络的小样本学习影响（此处以不同数据集大小的测试精度最大增量表征）。当Xd值较小时，神经网络的小样本学习性能随着缩放系数S值的增大而显著增强。例如，对于Xd=32，S从1.2 增大到2.0 可引起测试精度最大增量从6%上升至15%。随着缩放系数S值的继续增大，神经网络测试精度的最大增量呈现下降趋势，表明此时的网络模型对于高分辨率的图像数据出现欠拟合。当Xd=512 时，此时的全连神经网络对于S≤3.0 的不同分辨率图像数据集与未进行图像插值预处理的原始数据集具有等效性能，因而改变S值引起的测试精度最大增量可基本忽略。

表2 列出了Epoch=5 时的双线性插值不同缩放系数对卷积神经网络的小样本学习影响。当Xc值较小时，神经网络的小样本学习性能随着缩放系数S值的增大而增强。例如，对于Xc=4，S从1.2 增大到3.0 可引起测试精度最大增量从1%上升至6%。而对于较大Xc值（32 和128），此时的卷积神经网络对于S≤3.0 的不同分辨率图像数据集与未进行图像插值预处理的原始数据集具有等效性能，因而改变S值引起的测试精度最大增量可基本忽略。

2.5 不同插值算法的测试对比

图像插值算法不同，对原始图像中像素渐变关系的处理方式就会不一样。图5 分别给出了最邻插值、双线性插值以及双三次插值算法在MNIST 和USPS 手写数字图像集中的小样本学习测试结果。测试所选用的全连神经网络（细实线）的Xd= 32，卷积神经网络（粗实线）的Xc= 4，迭代次数Epoch 均为5。从图5 可以看出：（1）对于两种神经网络框架，MNIST 和USPS 数据集均具有相似的手写数字识别效果，说明此两数据集所采集的图像数据均有较好的完整性。（2）在两个数据集上，3 种插值方法在少量样本（尤其是N< 200）时对神经网络的预测精度均有明显提升。（3）与双线性插值效果接近，最邻插值和双三次插值也有效提升了神经网络对手写数字的识别性能。需要指出的是，对于不同的Xd和Xc值，3 种图像插值算法的测试结果均类似。（4）卷积神经网络（相比于全连神经网络）引入了额外的卷积层。神经网络架构、全连层与卷积层的神经元数目等不一样，训练参数数目等有很大差异。从整体效果来说，卷积层的参与使得卷积神经网络比全连神经网络（全连层架构及神经元数目一致）有相对更好的图像识别能力，特别是在小样本学习过程中表现更为明显。说明卷积算法有利于图像数据的特征提取，全连神经网络则对大数据集有更强的依赖性。图像插值预处理将全连神经网络的识别性能提升至与卷积神经网络在原始图像集类似的识别效果，此时的提升幅度较大（表1）；对于卷积神经网络，图像插值预处理可进一步提升识别精度，此时的提升幅度相对较小（表2）。

图5 不同图像插值算法在MNIST 和USPS 数据集的测试精度Fig.5 Test accuracy of different image interpolation algorithms in MNIST and USPS data sets

表1 双线性插值不同缩放系数的全连神经网络测试精度最大增量Table 1 The maximum accuracy increment of dense neural network with different S of bilinear interpolation

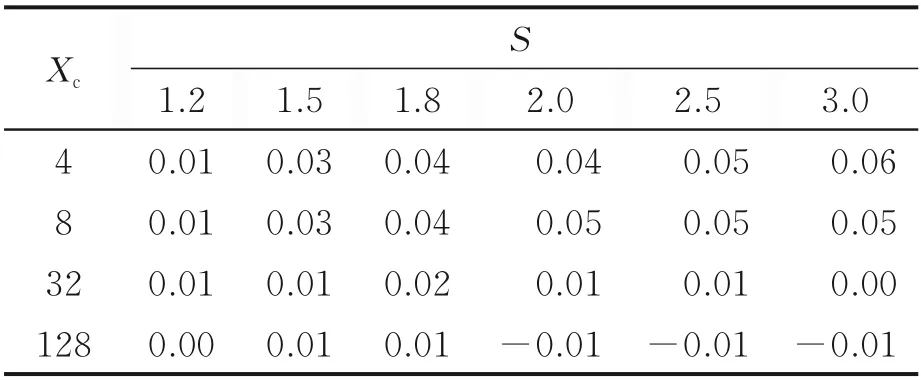
表2 双线性插值不同缩放系数的卷积神经网络测试精度最大增量Table 2 The maximum accuracy increment of convolutional neural network with different S of bilinear interpolation

3 结束语

针对深度神经网络对数据集的强依赖性问题，本文系统研究了基于图像插值的全连神经网络和卷积神经网络在小样本时的手写数字识别的学习性能。结果表明，图像插值在小样本学习中可显著提升模型性能；样本集越小，模型性能提升越明显。图像插值的预处理对全连接神经网络和卷积神经网络的影响程度不同，相比于原始数据集，对于包含两层全连接层的神经网络，图像插值预处理可引起最大约为15%的测试精度提升。对于一层卷积层堆叠两层全连接层的卷积神经网络，图像插值预处理可引起最大约为6%的测试精度提升。通过改变全连接层的神经元数、卷积层的过滤器数以及训练迭代次数的系统研究表明，图像插值可以有效提升神经网络在小样本学习中的特征提取能力和学习效率。需要说明的是，缩放系数决定了插值后图像的分辨率。对于相同的神经网络架构，输入图像的尺寸决定了可训练参数的数目以及模型最优化性能的超参数（如迭代次数等）选择。因此，最优化缩放系数的选择与原始图像质量、目标任务以及网络架构等有关。

图像特征是图像标识的基础，好的特征能够极大提高图像识别率。手写数字识别问题的关键是书写笔迹的特征提取。图像插值提高了图像的质量（分辨率），有利于神经网络（特别是卷积神经网络）的笔迹特征提取。因此，基于图像插值的策略有效提高了手写数字识别任务的计算精度，在小样本学习中效果更为明显。该策略有望应用到其他数据增强方法中。另外，3 种不同插值算法（最邻、双线性和双三次插值）在提升图像分辨率过程中引入了不同的图像边缘效果。对手写数字识别的小样本学习性能的相似测试结果说明，不同图像边缘效果对神经网络的书写笔迹特征提取并没有产生本质区别。在其他图像识别/分类任务（例如，机场等特殊场景的人脸多任务识别、多种类动值物分类和自动驾驶的场景标识与定位等）的小样本学习有待验证。在进一步的研究中，可将该方法拓展到其他计算机视觉问题，研究不同数据增强方法对不同深度网络架构小样本学习性能的影响。