隧道围岩中全长粘结式锚杆受力的非线性分析
赵宝华 金建伟 王光辉 黄明华 谭 鑫
(1.中铁隧道勘察设计研究院有限公司,广东 广州 511458;2.广东省隧道结构智能监控与维护企业重点实验室,广东 广州 511458;3.华杰工程咨询有限公司,北京 100029;4.湖南大学土木工程学院,湖南 长沙 410082)
锚杆因具有支护效果好、施工便捷和经济等优点,已被广泛应用于矿山、水利和土木等行业的围岩加固工程中[1-3]。针对隧道围岩中全长粘结式锚杆的加固机理,长期以来国内外诸多学者进行了较为系统研究。FREEMAN[4]通过观测支护过程中的锚杆应力分布,提出了中性点、粘结(拉拔)段以及锚固段的概念;TAO等[5]建立了中性点位置的理论表达式;王成[6]从承压拱的角度探讨了隧道围岩全长粘结式锚杆的设计计算理论;王超等[7]以锚固复合承载体为结构基础,推导出锚杆支护巷道最小支护力和最大允许变形量的表达式;吕爱钟等[8]采用复变函数方法分析了围岩全长粘结式锚杆的受力特性;通过定义变形剪应力和拉拔剪应力,LI等[9]以及姚显春等[10]将隧道围岩全长粘结式锚杆的加固区域划分为变形区、过渡区和稳定区,并给出了每个区域的界面剪应力表达式。上述研究为隧道围岩全长粘结式锚杆受力分析提供了有益参考,但均认为锚杆与围岩之间满足位移协调条件,未能有效考虑二者相对位移即界面剪切位移的影响。对此,蔡跃等[11-12]从剪滞理论出发,严格推导了隧道围岩全长粘结式锚杆锚固区段的线性界面模型,并给出了其受力特性分析的解析解,但没有考虑界面剪切刚度变化和剪切强度的影响。对此,已有学者[13-14]通过引入二折线型或三折线型等分段线性界面模型来研究隧道围岩全长粘结式锚杆的加固机理和受力特性,进一步考虑界面剪切刚度变化和剪切强度的影响。然而,线性或分段线性界面模型虽然便于获得隧道围岩全长粘结式锚杆受力的解析解,但却没有合理地刻画锚固界面剪切变形作用的非线性特性[15-17],即界面剪应力与剪切位移的非线性关系。
综上分析可知:已有研究大多采用线性或分段线性界面模型分析隧道围岩全长粘结式锚杆的受力特性,对于非线性界面模型的应用较少。为进一步开展隧道围岩全长粘结式锚杆的受力分析,本研究引入双曲正切函数来建立锚固界面剪应力与剪切位移的非线性模型,推导围岩变形作用下的全长粘结式锚杆荷载传递的非线性微分方程,并结合有限差分方法和Newton迭代公式给出锚杆轴力及界面剪应力的计算方法。在此基础上,结合典型隧道工程的锚杆实测结果,对围岩变形作用下的全长粘结式锚杆的受力特性及其影响因素进行分析,以期为隧道围岩锚杆设计和受力状态评价提供参考。
1 锚杆受力分析模型与荷载传递微分方程
1.1 隧道围岩锚杆受力分析模型
典型圆形隧道围岩中全长粘结式锚杆的布设情况如图1(a)所示,其中,r0为隧洞半径,r为隧洞径向坐标,ω为相邻锚杆之间的夹角,θ为所求点和洞心连线与水平方向的夹角。为建立锚杆的荷载传递微分方程,取锚杆杆体的微单元进行受力分析,如图1(b)所示。
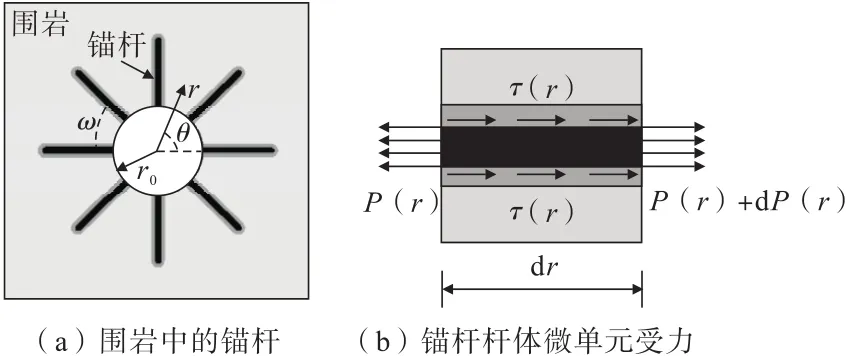
图1 隧道围岩中全长粘结式锚杆及其受力示意Fig.1 Schematic of full-length bond bolt and its stress in tunnel surrounding rock
假定锚杆轴力和界面剪应力均以图1(b)中箭头所示方向为正,则根据锚杆杆体微单元的受力平衡条件,可得到
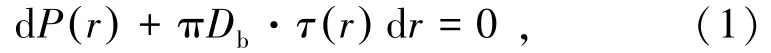
式中,P(r)和τ(r)分别为锚杆轴力和界面剪应力;Db为锚杆直径。
假设锚杆处于弹性状态,则有
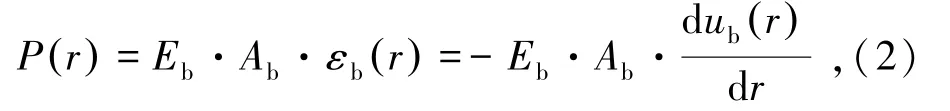
式中,Eb和Ab分别为锚杆的弹性模量和横截面积;εb(r)为锚杆的轴向应变;ub(r)为锚杆的轴向位移,以向隧道内部为正,与径向坐标轴正向相反。
将式(2)代入式(1)中,整理得到
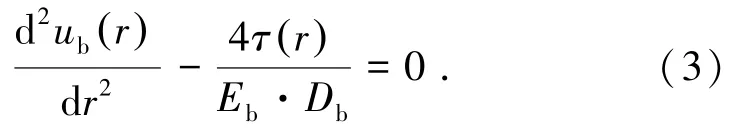
式(3)即为隧道围岩中全长粘结式锚杆荷载传递的基本方程,其关键在于确立ub(r)与τ(r)之间的函数关系,即建立界面层所传递的剪应力与对应剪切位移之间的关系。本研究定义界面层的剪切位移等于锚杆轴向位移与对应围岩径向位移之差,即
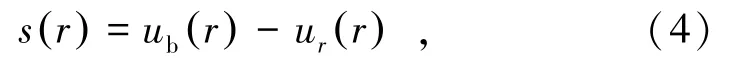
式中,s(r)为界面层的剪切位移;ur(r)为锚杆安装后围岩的径向位移。
1.2 锚固界面的双曲正切函数模型
指数函数模型[18]起初用于描述土体固结变形随时间的发展过程,之后被借鉴用于描述岩土体中界面层剪应力与剪切位移之间的非线性关系,但其要求剪切位移大于0,故不能直接用于描述围岩变形作用下的锚固界面剪应力与剪切位移的关系。鉴于此,本研究对指数函数模型进行改进,建立了界面剪应力与剪切位移关系的双曲正切函数模型
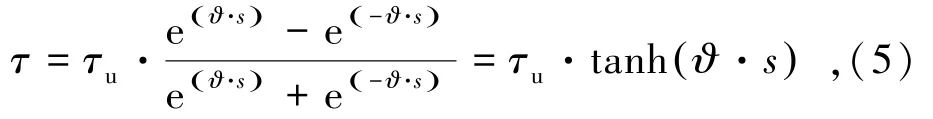
式中,ϑ为界面层剪切刚度系数,;k0为界面层的初始剪切刚度;τu为界面层的剪切强度;s为剪切位移。k0值可结合围岩和注浆体的剪切刚度[13,15]进行计算:

式中,kr为围岩的剪切刚度,硬岩一般取 5~10 GPa/m,软岩一般取1.5~3.0 GPa/m;km为注浆体的剪切刚度,与注浆体厚度和密实度等因素有关,可由下式进行计算:
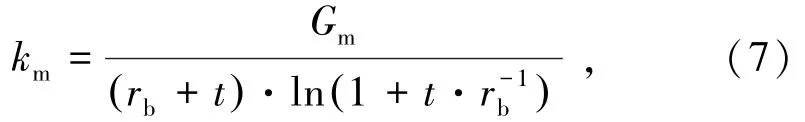
式中,Gm为注浆体的剪切模量;rb为锚杆半径;t为注浆体厚度。
τu一般满足Mohr-Coulomb屈服条件,即[13]
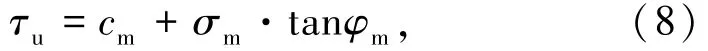
式中,cm和φm分别为界面的黏聚力和内摩擦角,与注浆体厚度、密实度等因素有关;σm为锚固界面受到的法向压力,主要与围岩应力、注浆压力等因素有关。
双曲正切函数模型所刻画的界面层剪应力与剪切位移的关系曲线如图2所示。作为对比,图中对应给出了理想弹塑性模型所刻画的界面层剪应力与剪切位移关系曲线。可以看出,理想弹塑性模型采用分段线性函数描述剪应力与剪切位移的关系,其中s0为最大弹性剪切位移;双曲正切函数模型则采用单一函数曲线描述剪应力与剪切位移的关系。随着界面剪切位移增大,界面剪应力逐渐增大,并最终趋于界面剪切强度,界面剪切刚度逐渐减小至0。
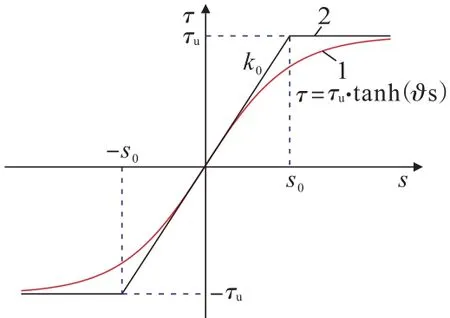
图2 剪应力与剪切位移关系曲线Fig.2 Relation curves between shear stress and interfacial slip
1.3 锚杆荷载传递非线性微分方程
将式(3)中的界面剪应力项τ(r)用式(5)进行代替,得到:
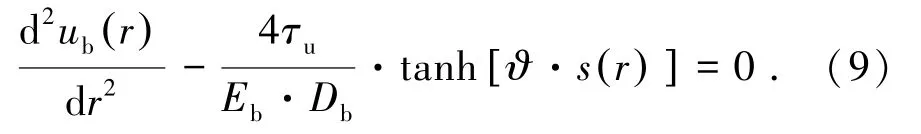
对式(9)两端求一次导,得到:
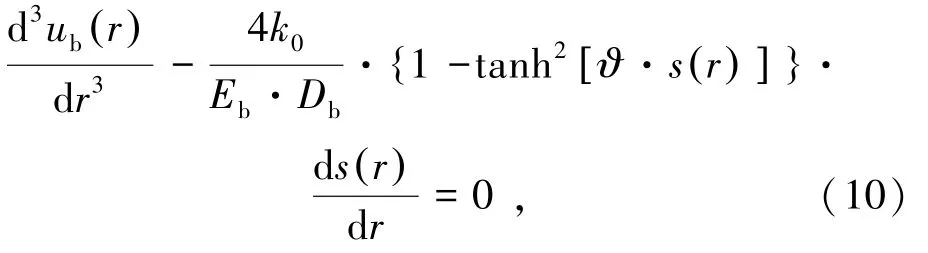
联立(9)和(10)两式,并利用式(2)和式(4),整理得到:
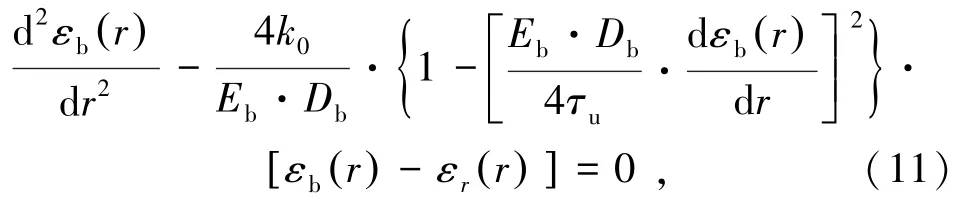
式中,εr(r)为锚杆安装后围岩的径向应变。
锚杆安装后,围岩受到初始地应力与锚杆约束力共同作用,所产生的围岩径向应变εr(r)为
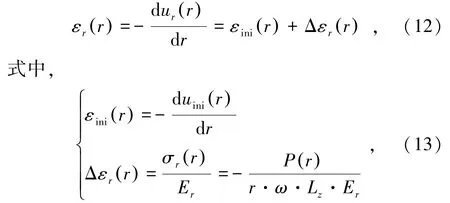
式中,σr(r)为围岩径向应力;Er为围岩弹性模量;Lz为锚杆沿隧洞纵向的布设间距;ω为相邻锚杆之间的夹角;εini(r)和uini(r)分别为锚杆安装后,由初始地应力所产生的围岩径向应变和位移,可用下式表示为[8]
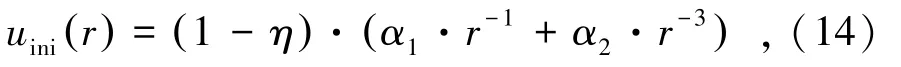
式中,系数α1和α2计算公式为
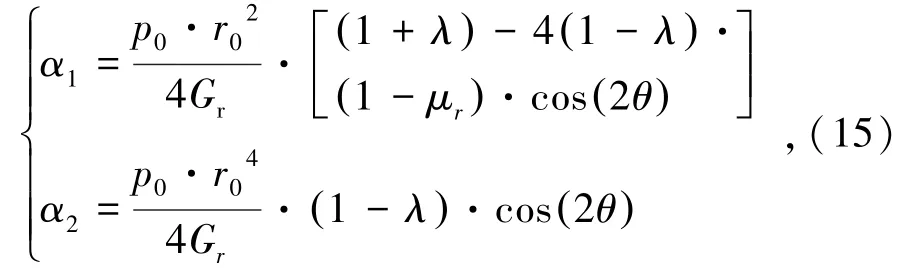
式中,η为围岩径向位移释放系数;p0为围岩初始地应力;λ为侧压力系数;Gr和μr分别为围岩剪切模量和泊松比。
将式(2)及式(12)至式(14)代入式(11)中,整理得到锚杆的荷载传递微分方程为
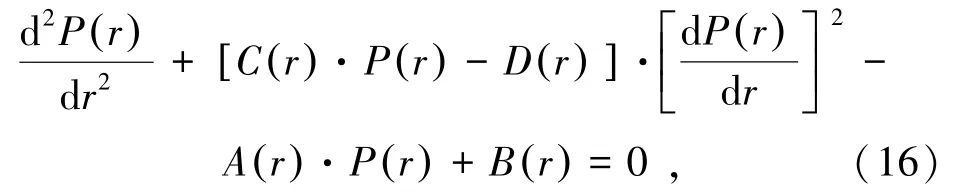
式中,A(r)、B(r)、C(r)和D(r)为与隧洞径向坐标r相关的4个函数,表达式为
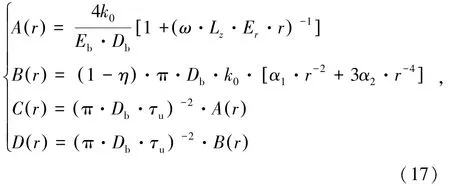
本研究仅考虑围岩变形作用且假设锚杆端部不设置垫板,故方程的边界条件可表示为
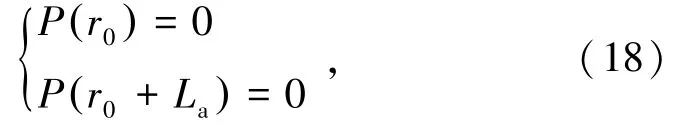
式中,r0为隧洞半径;La为锚杆长度。
2 荷载传递方程迭代求解
2.1 锚杆荷载传递方程离散化
式(16)为非线性二阶微分方程,直接求解存在较大困难。本研究首先基于有限差分方法对该非线性微分方程进行离散化,之后采用Newton迭代法对其进行迭代求解。沿锚杆长度方向将其离散为n段,即设置n+1个节点,节点编号依次为i=0,1,…,n,相邻节点之间的距离为Δr。对于内部节点i(1≤i≤(n-1)),本研究采用二阶中心差分格式可将式(16)离散为
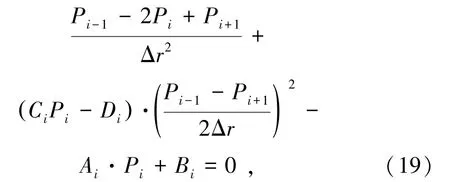
式中,Pi为锚杆在节点i处的轴力;Ai、Bi、Ci和Di分别为A(r)、B(r)、C(r)和D(r)在节点i处的取值。同时,根据边界条件(式(18))可知

式中,P0为锚杆在r=r0处的轴力,Pn+1为锚杆在r=r0+La处的轴力。
考虑上述边界条件,非线性有限差分格式可表示为一个n-1维的非线性系统即非线性方程组
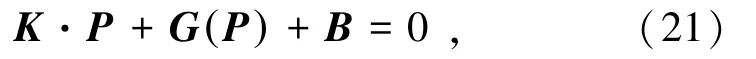
式中,K为系数矩阵;B为常数向量;P为锚杆轴力向量;G(P)为P的函数向量,相应的表达式为
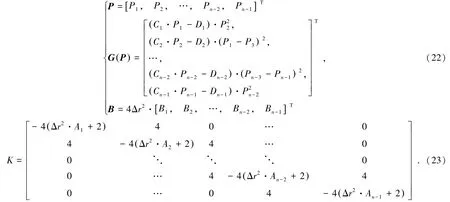
2.2 锚杆荷载传递方程迭代求解
令F(P)=K·P+G(P)+B,假定其一阶偏导数存在,则其Jacobi矩阵为
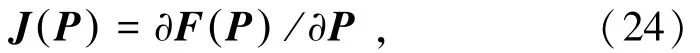
式中,J(P)为F(P)的 Jacobi矩阵。设为非线性方程组F(P)=0即式(21)的近似解,则根据Newton迭代公式有下式成立:

本研究通过有限差分法离散及构建Newton迭代格式将锚杆荷载传递微分方程(式(16))转化为非线性方程组(式(21))的迭代求解问题。具体实施步骤为:选取初始近似值P(0)代入式(25)中,可以求得一次近似值P(1);之后,将P(1)代入式(25)中,如此循环迭代计算,直至m次迭代后使得‖P(m+1)-P(m)‖<ε为止,其中ε为误差容许值。此时,P(m+1)为非线性方程组(式(21))的最终解,即锚杆轴力值。进一步由锚杆轴力值进行差分计算,可得出界面剪应力值。
3 算例与参数分析
3.1 算例分析与验证
选取日本长崎Holland-Zaka隧道[12]作为工程实例进行分析,以验证本研究建立的双曲正切函数模型及锚杆受力特性计算方法的正确性和适用性。该工程主要参数为:隧道埋深和半径分别为21 m和4.75 m,所受初始地应力为1 MPa,岩体弹性模量和泊松比分别为0.5 GPa和0.35,锚杆长度为4.0 m,沿隧道纵向和周向的布设间距分别为1.2 m和1.4 m,锚杆直径为25.4 mm,弹性模量为210 GPa。该隧道锚杆轴力实测值如图3(a)所示。借鉴文献[12]的研究成果,锚固界面剪切强度取1.25 MPa。同时,结合锚杆轴力实测值,采用最优化方法确定的锚固界面初始剪切刚度和围岩径向位移释放系数分别为3.0 GPa和0.69。此外,考虑到沿锚杆轴向2.5 m以外的轴力测点实测值为0,即该范围内锚杆不受力。现场试验观测表明[12],锚固界面在该范围内因注浆压力不足等因素出现了脱粘现象,不发挥作用,因此锚杆的计算长度分别取2.75 m和4.0 m。将上述参数代入本研究计算模型中,可得到锚杆轴力和界面剪应力的分布曲线,如图3所示。
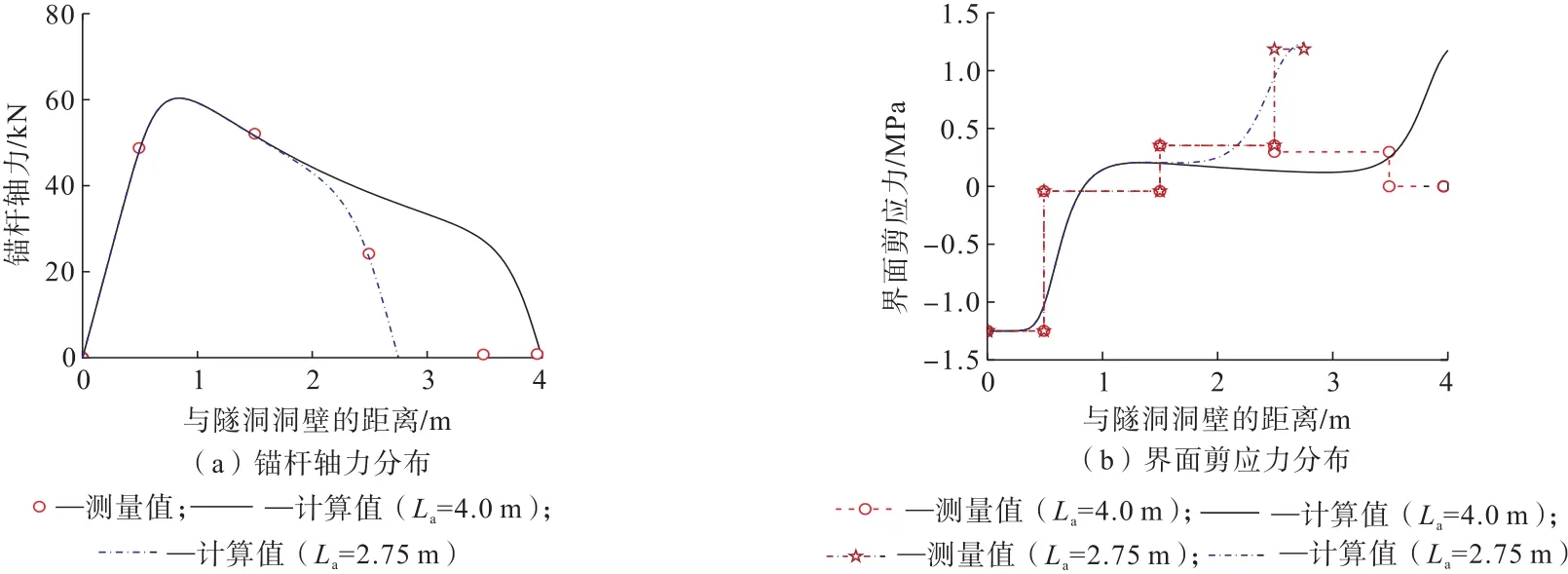
图3 Holland-Zaka隧道锚杆轴力与界面剪应力分布Fig.3 Distributions of axial force and shear stress of rock bolt in Holland-Zaka tunnel
分析图3可知:当锚杆计算长度取4.0 m时,锚杆轴力和界面剪应力计算值在沿锚杆轴向0~2 m范围内与实测值吻合得很好,而在沿锚杆轴向2~4 m范围内与实测值存在较为明显的差异,其主要原因是没有考虑锚杆远离洞周一端的锚固界面脱粘现象。当锚杆计算长度取2.75 m时,即考虑上述锚固界面的脱粘现象后,锚杆轴力和界面剪应力计算值在沿锚杆轴向范围内均与实测值一致,从而验证了本研究所建立的双曲正切函数模型及锚杆受力特性计算方法的可行性。
3.2 参数分析与讨论
在上述工程实例分析的基础上,通过依次改变锚杆长度La、界面剪切强度k0和初始剪切刚度τu以及围岩径向位移释放系数η的取值,对非线性界面模型下隧道围岩中全长粘结式锚杆的受力特性展开分析。
3.2.1 锚杆长度对轴力和剪应力分布的影响
锚杆长度分别取为 1.0、2.0、3.0、4.0、5.0 m,计算得到的锚杆轴力及其界面剪应力分布曲线如图4所示。
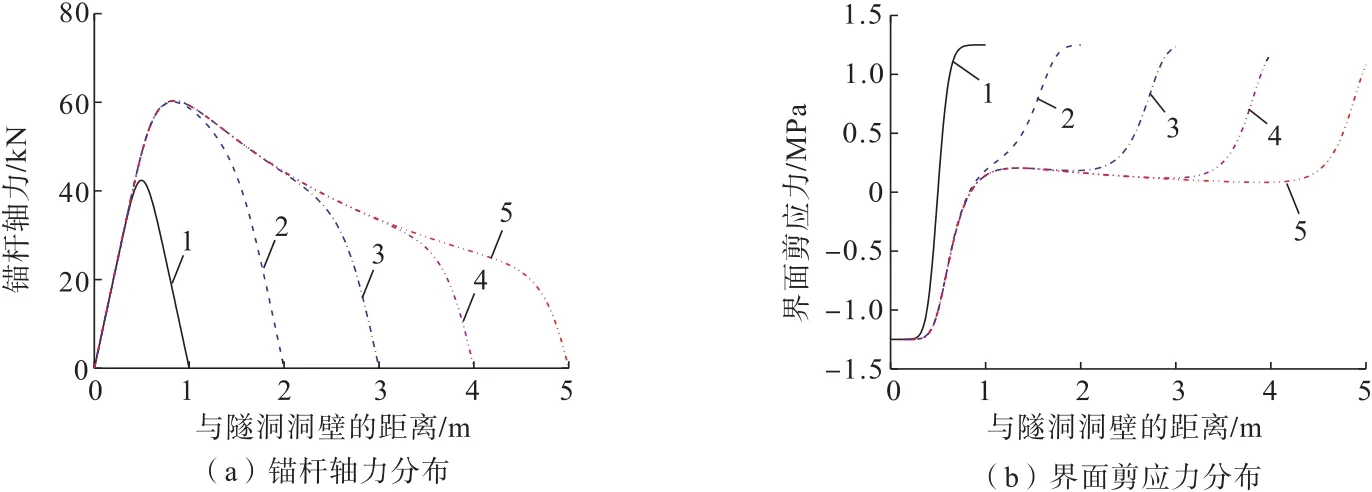
图4 不同锚固长度下锚杆轴力与界面剪应力分布Fig.4 Distribution of axial force and shear stress of rock bolt with different lengths
分析图4可知:不同长度条件下,锚杆长度对其轴力与界面剪应力的分布有较为显著的影响。随着锚杆长度增加,锚杆轴力及其界面剪应力分布逐渐向围岩深部传递。当锚杆长度较小(如小于2.0 m)时,随着锚杆长度增大,其轴力有较为明显的增加,即此时增大锚杆长度可显著提升锚杆对围岩的锚固力,同时锚固界面中性点(剪应力值为0)位置也随之向围岩深处偏移;然而,当锚杆长度较大(如大于2.0 m)时,随着锚杆长度增大,其最大轴力将逐渐趋于定值,不再增加,且锚固界面中性点位置也逐渐趋于稳定。此时,在锚杆粘结段内(隧道临空面至中性点位置)的轴力与界面剪应力分布不再随着锚杆长度的增加而变化,在锚杆锚固段内(中性点位置至锚杆末端)的轴力与界面剪应力则随着锚杆长度的增加而逐渐向围岩深部传递,该区段前部所提供的界面剪应力则逐渐减小,即此时锚杆锚固力主要由界面层远端所提供,其大小基本不变。由此可见,一定围岩变形作用下,增加锚杆长度虽然可提高锚杆的锚固力,但其存在临界值;超过临界值后,增加锚杆长度虽然可将界面剪应力传递至围岩深部,但其所提供的锚固力基本不变。
3.2.2 界面剪切强度对轴力和剪应力分布的影响
锚固界面剪切强度分别为 0.25、0.5、1.0、1.5、2.0MPa,计算得到的锚杆轴力及其界面剪应力分布曲线如图5所示。由图5可知:当锚固界面的剪切强度较小时,锚固界面剪应力在粘结段和锚固段内均呈均匀分布,对应地,锚杆轴力呈三角形分布;随着锚固界面剪切强度增加,锚杆轴力逐渐增大,即其提供的锚固力增加,锚固界面中性点位置逐渐向隧道临空面一侧移动,从而使得锚杆粘结段减小而锚固段增加,同时界面剪应力也逐渐向隧道临空面和锚杆末端聚集转移,而在锚固界面中间段很小,即此时锚杆锚固作用力主要由其远端界面层提供,而中间段锚固界面的剪切强度尚未充分发挥作用。
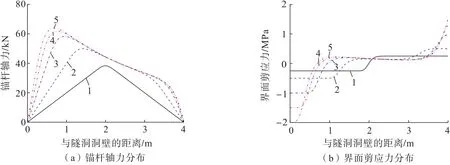
图5 不同界面剪切强度下锚杆轴力与界面剪应力分布Fig.5 Distribution of axial force and shear stress of rock bolt with different interfacial strengths
3.2.3 界面剪切刚度对轴力和剪应力分布的影响
锚固界面剪切刚度分别为 1、2、5、10、20 GPa,计算得到的锚杆轴力及其界面剪应力分布曲线如图6所示。分析图6可知:随着锚固界面剪切刚度增加,锚杆轴力逐渐增大,界面剪应力逐渐向隧道临空面和锚杆末端聚集转移,中性点位置移向隧道临空面一侧。主要原因是:锚杆与隧道围岩之间产生的剪切位移相同时,剪切刚度越大的锚固界面所能传递的剪应力越大,从而使得锚杆所能提供的锚固作用力也越大。实际工程中,宜采用压力注浆等方式来提高注浆体的施工质量,以确保锚杆与围岩之间的界面层能更有效地传递荷载。
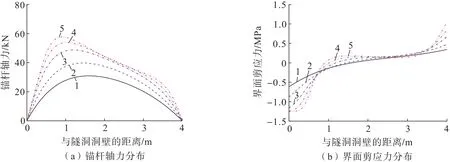
图6 不同界面剪切刚度下锚杆轴力与界面剪应力分布Fig.6 Distribution of axial force and shear stress of rock bolt with different interfacial stiffnesses
3.2.4 位移释放系数对轴力和剪应力分布的影响
锚杆施工前,隧道围岩已释放位移的大小即位移释放系数直接关系着锚杆的受力及其锚固效果。取围岩径向位移释放系数分别为 0.1、0.3、0.5、0.7、0.9,计算得到锚杆轴力及其界面剪应力的分布曲线如图7所示。
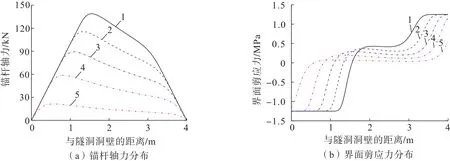
图7 不同位移释放系数下锚杆轴力与界面剪应力分布Fig.7 Distribution of axial force and shear stress of rock bolt with different released displacements
由图7可知:围岩位移释放系数越小,锚杆轴力越大即其在支护后所提供的锚固力越大,同时锚固界面剪应力取值及其分布范围也越大。因此,当围岩位移释放系数较小即锚杆支护施作较早时,应适当增加锚杆长度和直径,以提高锚杆的承载能力。当围岩位移释放系数很大即围岩已释放大部分位移时,锚杆在支护后所提供的锚固力很小,难以对隧道围岩形成有效的约束和支撑。在实际工程中,应根据隧道围岩的稳定状态以及所需锚固力的大小,及时施作锚杆支护。
4 结 论
本研究基于锚固界面剪应力与剪切位移的双曲正切函数模型,推导了围岩变形作用下全长粘结式锚杆的荷载传递方程。采用有限差分方法和Newton迭代公式建立了锚杆受力特性计算方法,并利用典型隧道工程锚杆试验实测结果验证了计算方法的合理性。主要得到以下结论:
(1)双曲正切函数模型采用单一函数曲线刻画了界面剪应力与剪切位移的非线性关系。随着界面剪切位移值增大,界面剪应力值逐渐增大,并最终趋于界面剪切强度,界面剪切刚度则逐渐减小至0。
(2)增加锚杆长度可提高其锚固力,但存在临界值;超过临界值后,锚杆锚固力基本不变;随着界面剪切强度和刚度增加,锚杆锚固力逐渐增大,中性点位置逐渐移向临空面,界面剪应力向临空面和锚杆末端聚集;围岩位移释放系数越小,锚杆支护后所提供的锚固力越大。工程实践中,应根据所需锚固力的大小,合理确定锚杆支护时机和长度。
(3)结合典型隧道工程锚杆实测结果,验证了所建立界面模型与锚杆受力计算方法的可靠性。在合理选择界面模型的基础上,锚杆受力特性分析的关键在于有效确定锚固界面的力学特性参数取值,故今后需对其取值方法展开进一步研究。

