不同等级岩巷力学参数赋值与素喷支护效果评价

袁海平 叶晨旭 王文辉

(合肥工业大学土木与水利工程学院，安徽 合肥 230009)

矿山巷道开挖过程中有效确保其周边围岩稳定是支护设计的关键所在，围岩内部节理和软弱夹层会导致围岩强度各不相同，为保证设计的合理可靠性，现场需进行原位强度测试分析[1]。但原位试验因施工条件限制有时无法实施，加之相关巷道支护设计规范欠缺[2]，给支护设计带来了困难。目前针对这一问题主要通过对围岩质量进行等级划分[3]，再根据围岩等级范围指导施工[4]，常用的围岩质量等级划分标准有RMR法[5]和BQ法[6]。但两者受自身影响因素限制，在复杂的矿山巷道中应用存在一定的不足。

Hoek-Brown强度准则是由 E.Hoek和 E.T.Brown于1980年提出，在经过不断的工程检验后，该准则得到了众多业内学者认可，并得到了广泛的应用研究[7]。HOEK针对RMR法在岩体十分破碎时偏差性较大的局限性，提出了地质强度指标(Geological Strength Index，GSI)[8]，并给出了相应的岩体参数经验取值方法(广义Hoek-Brown强度准则)[9-10]。近年来，国内许多学者对Hoek-Brown强度准则和GSI法开展了广泛研究，取得了一定的进展。张丙先[11]结合完整性指数Kv与Hoek-Brown经验公式来分析GSI指标的变化，对深部断裂构造岩体的抗剪强度和变形模量进行了估算;姜谙男等[12]将Hoek-Brown准则应用于隧道围岩，改进了单元安全度公式，实现了对单元不同力学状态的表达;闫长斌等[13]考虑了岩体爆破损伤及其累积效应，指出了Hoek-Brown准则及其改进公式的不足，提出了岩体经验参数mb和s的修正取值方法。上述成果针对Hoek-Brown强度准则和GSI法的研究集中在理论层面，主要从影响因子角度对公式进行修正改进，但在工程应用方面稍有欠缺。

本研究基于Hoek-Brown强度准则和GSI法，对矿山巷道支护效果预先进行安全性分析，建立了不同岩体质量等级、不同支护参量与支护效果最小安全系数的经验表达式，实现支护结构安全性的定量化描述，结合现场勘察结果验证了该方法的可行性，并进一步分析了Hoek-Brown强度准则和GSI法的工程应用效果，以期为实际施工提供借鉴。

1 地质强度指标(GSI)评价法

1.1 Hoek-Brown强度准则

Hoek-Brown强度准则可以体现岩石极限破坏状态时最大、最小主应力之间的经验关系，自20世纪80年代起该准则被大范围应用于地下工程与边坡工程[14]。HOEK等[15]在考虑工程施工对岩体性能的影响时引入了“岩体扰动”概念，添加了一个反映工程影响的岩体扰动参数D，并给出了相应的岩体质量经验参数计算公式:

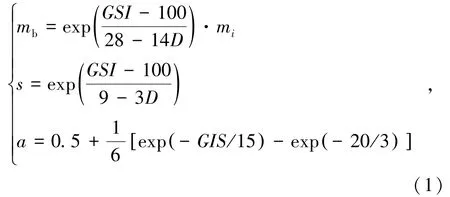
式中，mi为岩石量纲一的经验参数，0.001～25.000;mb、s、a为反映岩体质量的经验参数，其中mb、a为针对不同岩体的量纲一的经验参数，s参数用于描述岩体破碎程度，0～1;D为岩体扰动系数，0～1，岩体扰动程度越大，D越大。

1.2 地质强度指标GSI

Hoek-Brown强度准则早期主要应用于室内试样分析，如何将室内岩块与现场岩体联系起来，这是制约该准则推广应用的关键问题。最原始的思路是直接采用RMR岩体评分系统换算岩体力学性能参数，但在一些地质条件复杂的特殊地段，该方法分析结果与现场实际存在一定偏差。为解决这一问题，1994年HOEK[16]放弃了RMR岩体评分系统，提出了与Hoek-Brown强度准则相配套的地质强度指标GSI，该指标更加注重考虑岩体结构和结构面状态，岩体强度换算结果与现场实际较为吻合。1999年，SONMEZ和ULUSAY[17]针对GSI提出了系统性量化取值的评价方法，通过对岩体结构面表面特征、结构等级、扰动程度等指标分级取值，最后通过查阅地质强度指标(GSI)分级表插值获取GSI值[7]。

1.3 岩体参数

2002年HOEK等[15]参考不同工程对象，选取了相应的最大围压上限σ3max和抗拉强度σt，在两者范围内基于Mohr-Coulomb强度准则拟合Hoek-Brown强度准则(图1)。拟合表达式为

图1 等效Hoek-Brown和Mohr-Coulomb准则中最小和最大主应力的关系Fig.1 Relationship between minimum and maximum principal stresses in equivalent Hoek-Brown and Mohr-Coulomb criteria

式中，c为黏聚力，MPa;φ为内摩擦角，(°);mb、s、a为反映岩体质量的经验参数，其中mb、a为针对不同岩体的量纲一的经验参数，s参数用于描述岩体破碎程度;σ3n为标准化的主有效应力，σ3n=σ3max/σc;σc为抗压强度，MPa。

岩体变形模量可以通过岩样单轴抗压强度估算取值[18]，估算公式为

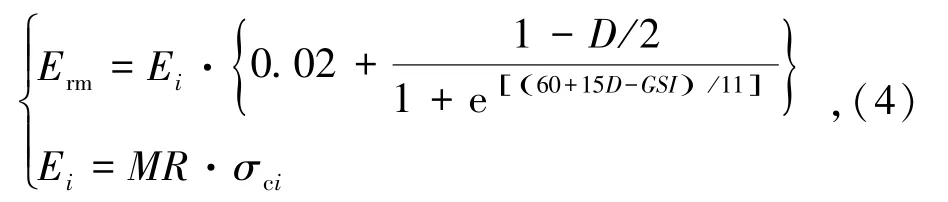
式中，Erm为岩体变形模量;Ei为岩体弹性模量;D为岩体扰动系数，0～1，岩体扰动程度越大，D越大;MR为模量比，通过已有试验或经验值查表获得;σci为岩样单轴抗压强度，MPa。

2 数值计算模型

本研究以华南地区某大型铁矿为例，建立数值计算模型。计算模型由一条三心拱巷道构成，直墙高2.9 m、拱高1.3m、宽度4m，模型长为20m，宽为15 m，高为34 m。为提高计算精度，对网格进行了简化，并对巷道周边网格进行了划分加密处理。计算模型共有793 761个单元(图2)。

图2 计算模型Fig.2 Calculation model

该模型主要模拟了采取素喷混凝土支护的矿山巷道在不同质量等级围岩作用下，围岩应力对支护结构稳定性的影响。巷道为一次开挖再支护形式，支护结构采取两种建模方案，一种采用实体单元，另一种采用壳型单元，按照标准C30混凝土赋予参数。工程现场岩性为大理化灰岩，岩体经验参数mi取10，岩体平均单轴强度取101.8 MPa，埋深假定500 m，上部岩层平均容重取26 kN/m3。采用矿山法将岩体划分等级(Ⅰ～Ⅵ级)，对应线性内插至GSI值(0～100)，将Ⅰ～V级均分为20份，即1～5级每隔0.2级取一次GSI值。由式(1)计算相应的岩体参数mb、s和a，再由式(2)、式(3)得到围岩力学参数c、φ，岩体变形模量在岩体单轴强度基础上由式(4)估算取得，所获得的岩体参数取值见表1。

表1 岩体力学参数Table 1 Mechanical parameters for rock mass

3 计算结果分析

围岩应力会对支护结构稳定性产生影响，当围岩应力较大时，支护结构会出现局部开裂，甚至破碎坍塌。本研究基于Hoek-Brown强度准则，从位移和应力两个方面分析围岩应力作用下的支护结构稳定性。

3.1 位移分析

结合开挖断面监测点的空间位移数据绘制了围岩质量等级与开挖断面监测点空间位移的关系曲线，如图3所示。由图3可知:随着围岩等级增长各监测点空间位移增大，在低围岩等级时曲线斜率稳定，而后逐渐增大，至高围岩等级时呈指数关系，这与混凝土的破坏机理相吻合;低围岩等级时支护厚度对开挖位移影响较小，高围岩等级支护厚度(8 cm)比支护厚度2 cm开挖位移减少约45%。

图3 拱顶位移与岩体等级、支护厚度关系曲线Fig.3 Relation curves between vault displacement and rock mass grade and support thickness

根据开挖断面监测点位移数据，绘制了开挖断面位移示意图，如图4所示。由图4可知:直墙位移最大处位于直墙中部，其位移趋势与拱顶位移相似，大体在岩体质量等级3级时快速增长，说明岩体质量等级在3级左右时支护体开始发生局部破坏。

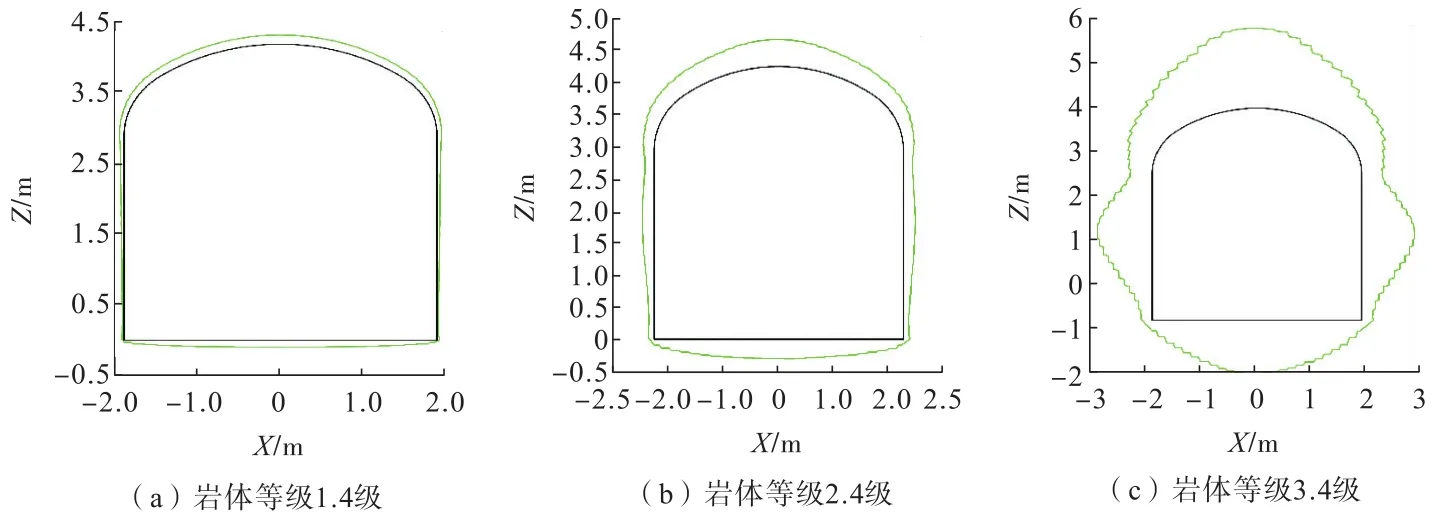
图4 横截面位移示意Fig.4 Schematic of cross section displacement

3.2 应力分析

针对当前巷道开挖位移警戒值无法确定的问题，本研究从材料力学角度给出了一种通过控制支护内部应力保证结构安全性的方法。巷道开挖后支护主要承受弯矩和轴力，因而支护主要呈弯曲抗压状态，为保证支护材料稳定性，内部应力需要控制在极限强度以内。根据《铁路隧道设计规范》(TB 10003—2016)[19]，C30混凝土弯曲抗压极限强度可取28.1 MPa。在第2种模拟方案中直接调用支护内部应力，取开挖截面水平方向为坐标面X轴，垂直方向为坐标面Y轴，各应力张量见图5。

图5 壳型单元应力张量Fig.5 Shell element stress tensor

本研究通过内部应力与极限强度的比值计算开挖截面各点的安全系数，公式为

式中，Fs为安全系数;[σ]为应力极限强度，取28.1 MPa;σ为内部应力，MPa。

验算施工阶段强度时，根据《公路隧道设计规范》(JTG 3370.1—2018)[20]要求，混凝土结构安全系数取1.8。由于隧道设计使用年限远大于矿山巷道，并考虑到混凝土结构在弯压组合荷载作用下整体偏于安全，故矿山巷道支护强度的安全系数取1.2。基于式(6)绘制了开挖断面安全系数分布图，并对安全系数低于1.2的区域进行了标注(图6)，发现支护薄弱点位于左右拱段，随着围岩等级逐渐增大，拱部各点安全系数下降趋于平缓。对安全系数数据分析可知，从岩体质量等级3.0级开始薄弱处安全系数降至1以下，说明支护体已经开始发生了局部破坏，破坏不断延伸最终形成塑性区贯通导致整体破坏。

图6 开挖断面安全系数分布示意Fig.6 Schematic of the distribution of safety factor of excavation section

为保证支护结构稳定性，本研究通过计算最小安全系数给予施工建议，以便提前对支护薄弱处进行处理。对不同支护厚度方案提取开挖截面最薄弱处的安全系数，绘制了不同支护厚度下的岩体等级与最小安全系数关系曲线，如图7(a)所示。

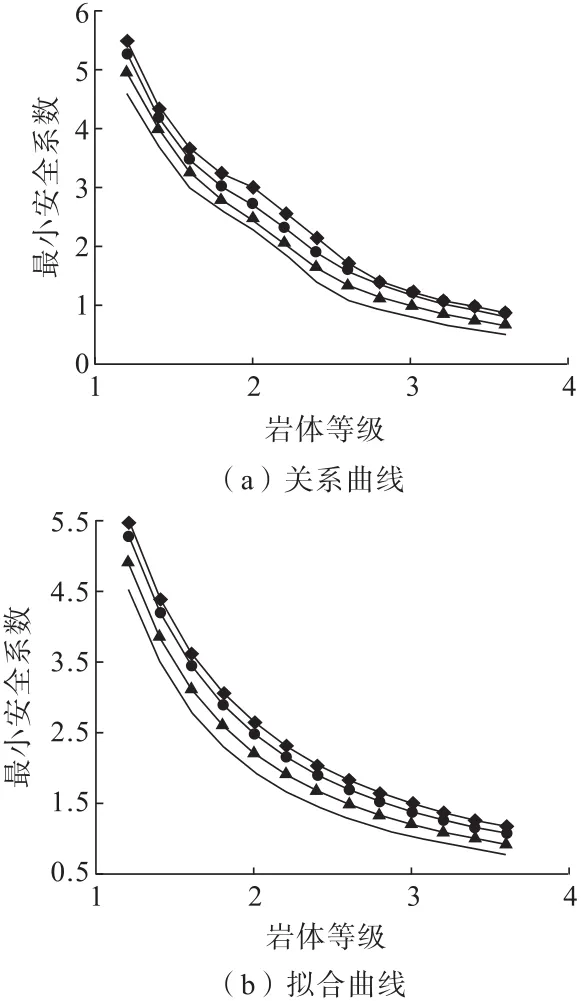
图7 岩体等级与最小安全系数关系曲线和拟合曲线Fig.7 Relation curve and fitting curve between rock mass grade and minimum safety factor

本研究从统计学角度分析岩体等级与最小安全系数的相关性，采用相关系数来衡量两者的线性关系，公式为

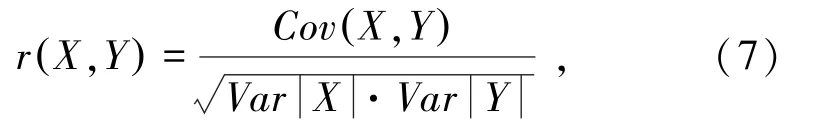
式中，r(X，Y)为X与Y的相关系数;Cov(X，Y)为X与Y的协方差;Var为X的方差;Var为Y的方差。

经计算，图7(a)所示4条曲线对应的相关系数分别为-0.953 3、-0.951 5、-0.955 5和-0.963 2，说明岩体等级与最小安全系数之间具有高度的线性负相关性，即岩体等级、支护厚度和最小安全系数分别对应自变量、函数变量和因变量。根据曲线分析两者大致呈幂函数曲线关系，函数关系形似y=d·xe+f，通过Matlab软件将其转化为线性曲线，线性回归后得到4条曲线的函数变量d、e、f(表2)。

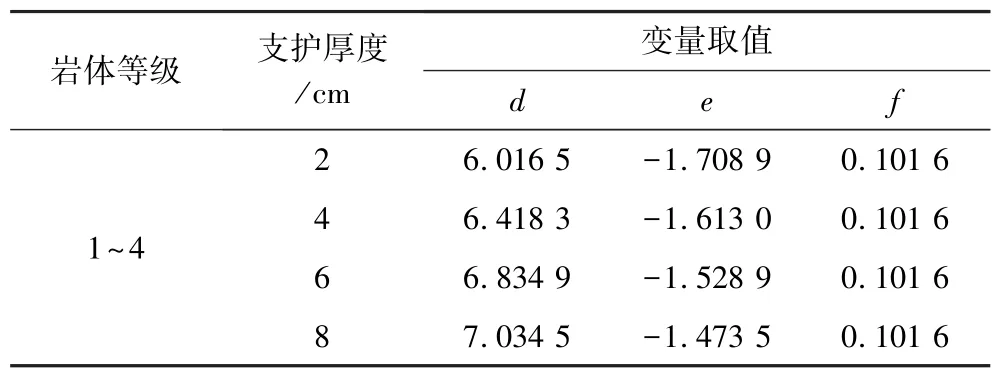
表2 线性回归函数变量取值Table 2 Variable values of linear regression function

在线性回归函数的基础上重新绘制拟合曲线(图7(b))，与原曲线比对发现拟合效果较好，在此基础上建立了针对素喷支护开挖最小安全系数的经验表达式:

式中，d、e、f为函数变量，由支护厚度决定;x为岩体等级。

当确定现场巷道岩体等级与支护厚度时，采取对应的函数变量和自变量，利用式(8)可以方便获得针对该工程素喷支护下开挖断面的最小安全系数，可用来快速判断支护局部是否产生破坏，从而给现场施工提供参考。

在施工现场布点监测支护破损情况，结合监测点周边岩体等级，利用式(8)计算分析最小安全系数，对比分析发现两者吻合度较高，说明该方法可以应用于实际工程施工。因而在施工前可以采用数值模拟软件对开挖工况进行模拟计算，对巷道截面进行安全评估，寻找施工薄弱点，便于提前进行加固处理，提升支护整体稳定性，优化支护设计。

4 结 论

(1)通过先参数赋值再建模的思路，得到基于现场岩性和支护形式的最小安全系数经验表达式，再根据岩体等级和支护厚度采用不同的函数变量计算最小安全系数。为确定现场巷道岩体等级与支护厚度时，可以通过计算最小安全系数快速判断支护效果，实现矿山巷道快速按需支护设计及其支护效果评价，从而为现场施工提供有益参考。

(2)绘制了开挖截面的安全系数包络图，可直观寻找支护体系薄弱点，为工程施工提供指导。矿山巷道岩体等级分布变异较大，本研究提出的岩体质量等级、支护厚度与支护结构安全系数关系的拟合经验公式，为矿山不同等级岩巷力学参数赋值、快速按需支护设计及其支护效果评价提供了新思路。

(3)该方法仅针对单一工程进行了分析，后期仍需提取不同岩性、不同支护类型的矿山巷道支护数据进一步分析其工程适用性和适用范围。