基于VMD分解与MIC特征分析的风电功率组合预测

甄成刚，张争鹏

(华北电力大学 控制与计算机工程学院 河北 保定 071003)

0 引言

风能作为一种蕴量巨大的清洁可再生能源，已得到大力的发展。由于自然风的波动性与随机性，导致风电功率本身的不确定性。随着风电机组的大量并网，影响着电力系统运行的可靠性和安全性[1]。因此风电功率的准确预测可以保障风电场的运行稳定性，减轻电网系统的调度负担。

目前风电功率的预测采用条件预测法[2]、概率预测法[3]、区域网格预测法[4]以及组合预测法[5]等。组合预测模型综合利用不同模型的处理性能，有效提高了预测结果的精度[6]。Yang等[7]利用模糊C均值聚类将相似的功率特性分类，选取最具代表性的功率曲线作风电场的等效曲线，但没有考虑预测样本之间的内在波动以及对时间段的划分；叶林等[8]利用最大相关最小冗余原则选择气象特征因素划分天气波动过程，建立波动过程关联的组合预测模型，但只根据风速的波动特性划分不同的天气过程，忽略了环境温度、风向等的影响；王佶宣等[9]结合经验模态分解与径向基神经网络进行预测，但经验模式在分解过程中受干扰易出现模态混叠；林涛等[10]建立气象信息和操作条件的组合预测模型，证明了风电机组运行条件对功率输出的影响，但没有对各单一的影响因素进行分析。

基于上述内容分析,本文提出了一种基于监视控制与数据采集(supervisory control and data acquisition，SCADA)的风电功率预测的多变量综合模型。为了挖掘数据中潜在的周期特性,采用变分模态分解(variational mode decomposition，VMD)将原始风电功率数据分解为多个本征模态函数(intrinsic model function，IMF)分量；针对每个IMF分量考虑其影响因素，采用最大信息系数(maximal information coefficient，MIC)进行输入特征的选择；为每个IMF分量建立基于诱导有序加权平均算子的组合预测模型，最后对所有IMF的预测结果进行整合。本方法在考虑风电的波动性、随机性、间歇性等多种特性的同时，还考虑气象因素和风机的能量转化过程，对每个IMF分量都选择预测精度最高的特征组合，使预测结果更为准确。

1 风电功率预测方法研究

1.1 VMD算法原理

变分模态分解[11]是一种自适应的信号处理以及完全非递归的模态变分的方法。该方法通过对原始信号分解得到多个平稳的不同频率子序列，实现IMF分量的分离，获得满足变分问题的解[12]。

1.1.1变分模型的构造 VMD要求各模态的估计带宽之和最小，约束条件为所有模态之和与原始信号相等，则相应约束变分模型的表达式为[13]

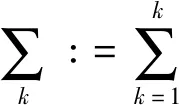
1.1.2变分问题的求解 引入二次惩罚因子α与Lagrange乘法算子λ(t)，将上述约束变分问题转变为非约束变分问题[14]，得到扩展的Lagrange表达式为

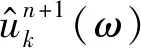
1.2 基于IOWA算子的组合模型

不变权的组合模型仅根据模型的类型进行模型权重的划分，各模型在整个预测区间的权重系数不变，使得在不同时点的组合预测结果达不到最优[15]。由此，采用诱导有序加权平均(induced ordered weighted average，IOWA)算子计算各单项模型的权重，得到变权的组合预测模型，最大程度减少预测过程的误差[16]。

定义1设二维数组(,…,,…,)是由时间点t下的m种单项模型的精度和预测值组成，并将数组中m个元素按照ait由大到小的顺序排列，则定义基于IOWA算子的组合模型预测值为

式中：a-index(it)表示按照ait大小排序后t时刻第i个精度的下标。

定义2定义ait为时间点t下第i种单项模型的预测精度,

令ea-index(it)=yt-ya-index(it)，则以误差平方和最小为准则的组合模型最优化公式为[17]

2 多影响因素分析方法

是以信息论为基础的衡量变量间数据关联性的一种方式，具有通用性和公平性。它假定在相关变量的数据散点图上绘制网格，以度量二者间的相关性[18]。

设X、Y为数据集中的两个随机变量，其中:X={x1,x2,…,xn}；Y={y1,y2,…,yn}；n为样本数。定义X和Y之间的互信息为

式中：p(x,y)为X和Y之间的联合概率密度；p(x)和p(y)分别为X和Y的边缘概率密度。

在变量x、y组成的数据散点图上进行相应网格的绘制，通过计算各网格的互信息来表征数据点落入网格的情况，在采用不同标准的网格划分下选取互信息的最大值作为最终的MIC值，计算公式为

其中：在x、y方向划分网格的个数分别为a、b，而划分网格的最大值为B。

3 风电功率预测模型

3.1 基于VMD-MIC-IOWA组合的风电功率预测

风电功率数据是一组波动且随机的时间序列，对其采用VMD分解获得的IMF分量包含这些特征信息。为了弥补分解过程中带来的信息缺失，利用更具普适性、公平性和对称性的MIC特征选择方法，选择出各个分量的影响特征并将其加入预测过程中，使模型结果更加精确。

各种预测模型都有其局限性，单一的网络模型在预测过程中不能有效避免模型自身存在的问题。基于此，采用结构简单、可挖掘序列内部时间规律的门控循环单元(gated recurrent unit，GRU)以及学习速度快、泛化性和稳定性好的最小二乘支持向量机(least squares support vector machine，LSSVM)两种模型来进行预测。

整体算法框架如图1。

图1 算法总体流程图Figure 1 Algorithm overall flow chart

3.2 预测精度评价指标

为了定量分析预测结果，采用的误差评价指标有决定系数(R2)、归一化的均方根误差(NRMSE)[19]。由于功率数据中存在零值，这里采用反正切绝对百分比误差(MAAPE)[20]。各评价指标的计算为

4 实验与结果分析

4.1 数据准备

选取江苏某风场8月的SCADA数据进行分析。该风场的采样频率为10 min。本文选择8月1日—8月24日的3 456条数据进行训练模型，8月25日—8月27日的432条数据进行模型测试。原始风电功率数据如图2。

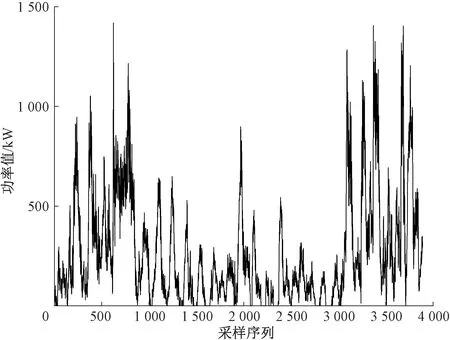
图2 原始数据Figure 2 Raw data

图3 VMD分解序列Figure 3 VMD decomposition sequence

在设置好信号的分解个数K和惩罚因子α后，使用VMD对原始信号进行分解。基于前期测试可知，K>5时后续子序列趋于相似，因此本文选择K=5，α=2 700。分解结果如图3。

4.2 特征选择

风力发电机的输出功率受环境因素与风机运行条件的综合影响，所以数据经VMD分解获得的各个IMF分量会包含这些特征信息。选择合适的输入特征集合可以优化模型性能，这些影响因素的输入可以降低分解过程造成的信息损失。

风机工作中能量由叶轮、变速箱到发电机之间逐级流动，这个过程存在时间上的滞后性；此外当前的功率数据与之前风机的工作状态有关，所以本文考虑时间序列前后联系的特征，采用MIC来选择各个分量的特征集合，为方便表示记此方法为MICT。

对采集到的SCADA数据进行预处理后，初选6个变量进行分析。设t时刻的相关特征：WS表示风速；WA表示风向角；T表示环境温度；RS表示叶轮转速；GS表示发电机转速；GT表示发电机温度。

本文选择的风机数据采样频率为10 min，因此表1中的时间t用10，20，30，…来表示；风速、环境温度等的历史值用WSt、Tt表示，代表t分钟前的历史值。

计算各个IMF分量的MIC值，降序排列依次输入预测模型。采用各输入序列预测结果的最小平均绝对百分比误差(MAPE)值作为输入特征的选择，选择结果如表1所示。

表1 IMF分量的特征选择Table 1 Feature selection of IMF components

从表1可以看出，IMF1、IMF3和IMF4主要包含风速、叶轮转速和发电机转速这些动量因素的特征；IMF2主要包含发电机温度信息的特征；而IMF5主要包括环境温度、风向角等气象信息特征。

4.3 预测结果分析

本文建立了基于气象信息的气象模型、基于气象信息和操作条件的SCADA模型来检验风机运行条件对输出功率的影响情况，记为模型一和模型二。图4为所述模型的预测结果。

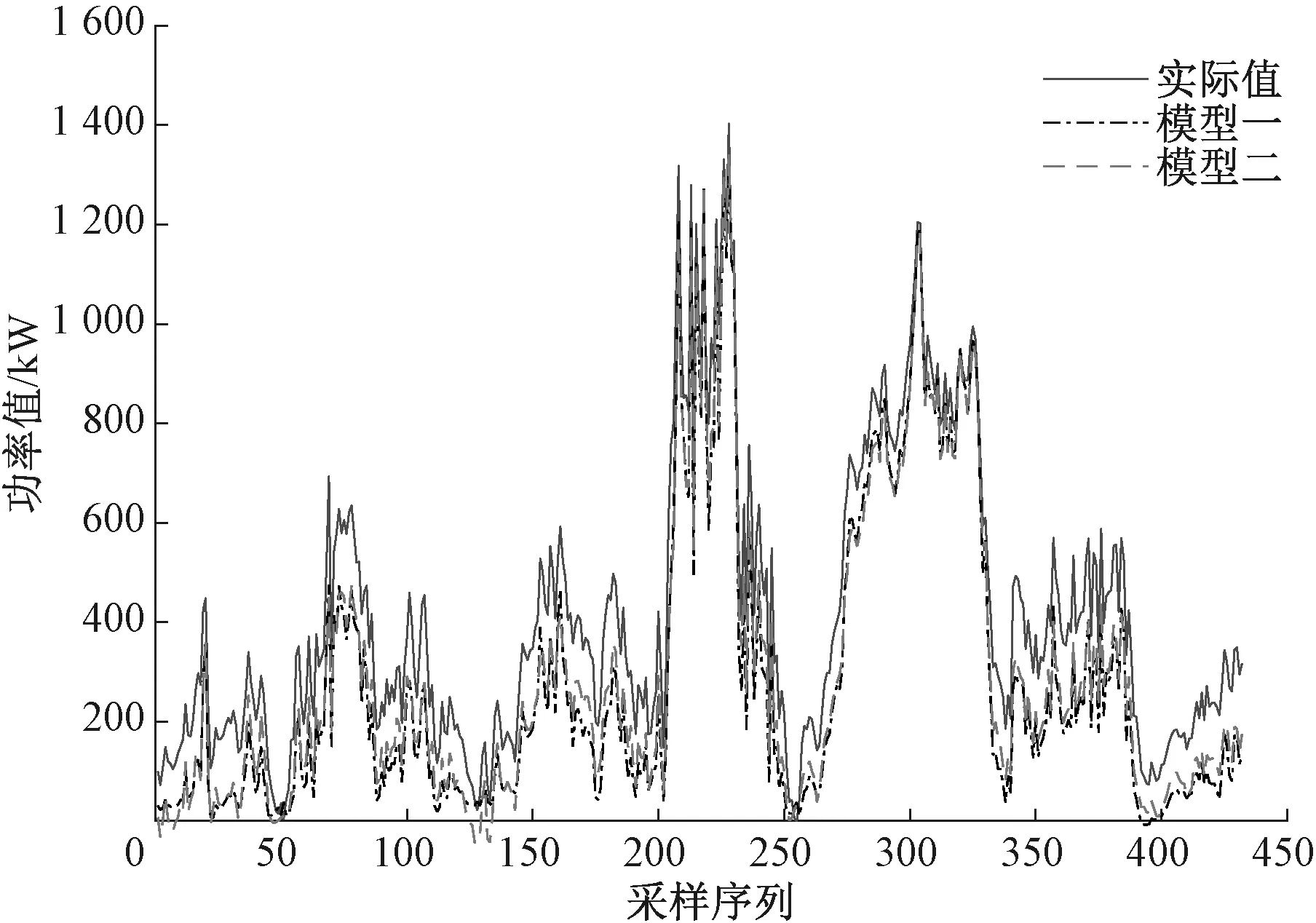
图4 模型的预测结果Figure 4 Forecast results of models

采用R2、NRMSE、MAAPE指标进行评价分析。

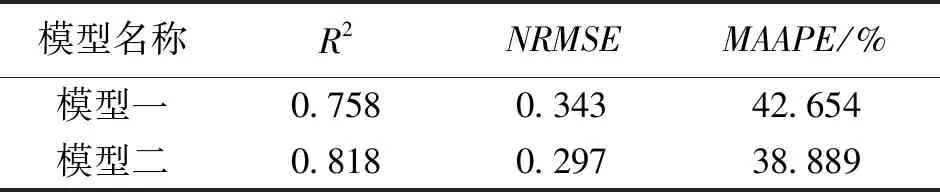
表2 两种模型的评价指标Table 2 Evaluation indicators of the two models

从表2可知，考虑气象信息和运行条件的综合模型的预测效果优于单一模型，但与风电功率的实际值偏离程度较大。

为了验证本文所提VMD-MICT-IOWA组合预测模型的有效性，还建立了多种组合预测模型进行对比分析。图5为这几种预测模型的预测结果。

计算各模型的R2、NRMSE、MAAPE指标,并进行评价分析，见表3。

图5 不同预测模型的效果Figure 5 The effect of different forecasting models

表3 各预测模型的评价指标Table 3 Evaluation index of each prediction model

由表3可知，本文所提模型的预测结果优于其他对比模型。较LSSVM模型，经IOWA算子变权后的组合模型提高了预测精度，并且具有较高的泛化能力。此外采用MIC方法选择特征后，预测结果得到提高。而考虑时间尺度的MICT方法利用特征因素对功率数据的复杂影响，进一步提高了对风电功率预测的准确度。

4.4 其他实验分析

为了进一步验证本文所提模型的泛化能力，选取与江苏风电场不同经纬度、不同型号的黑龙江某风电场风机进行实验验证。以该风电场11月的数据进行实验，该场每天采集144个点。本文用11月1日—10日共1 440条数据进行建模，将11、12日两天共288条数据用于进行测试。数据及预测结果如图6、7所示。

计算的模型评价指标如表4。

从上表可以看出，本文所提的组合预测模型精度最高，与江苏风电场的实验结果相吻合。通过对不同地区、不同型号的风机进行实验，验证了所提模型的有效性。

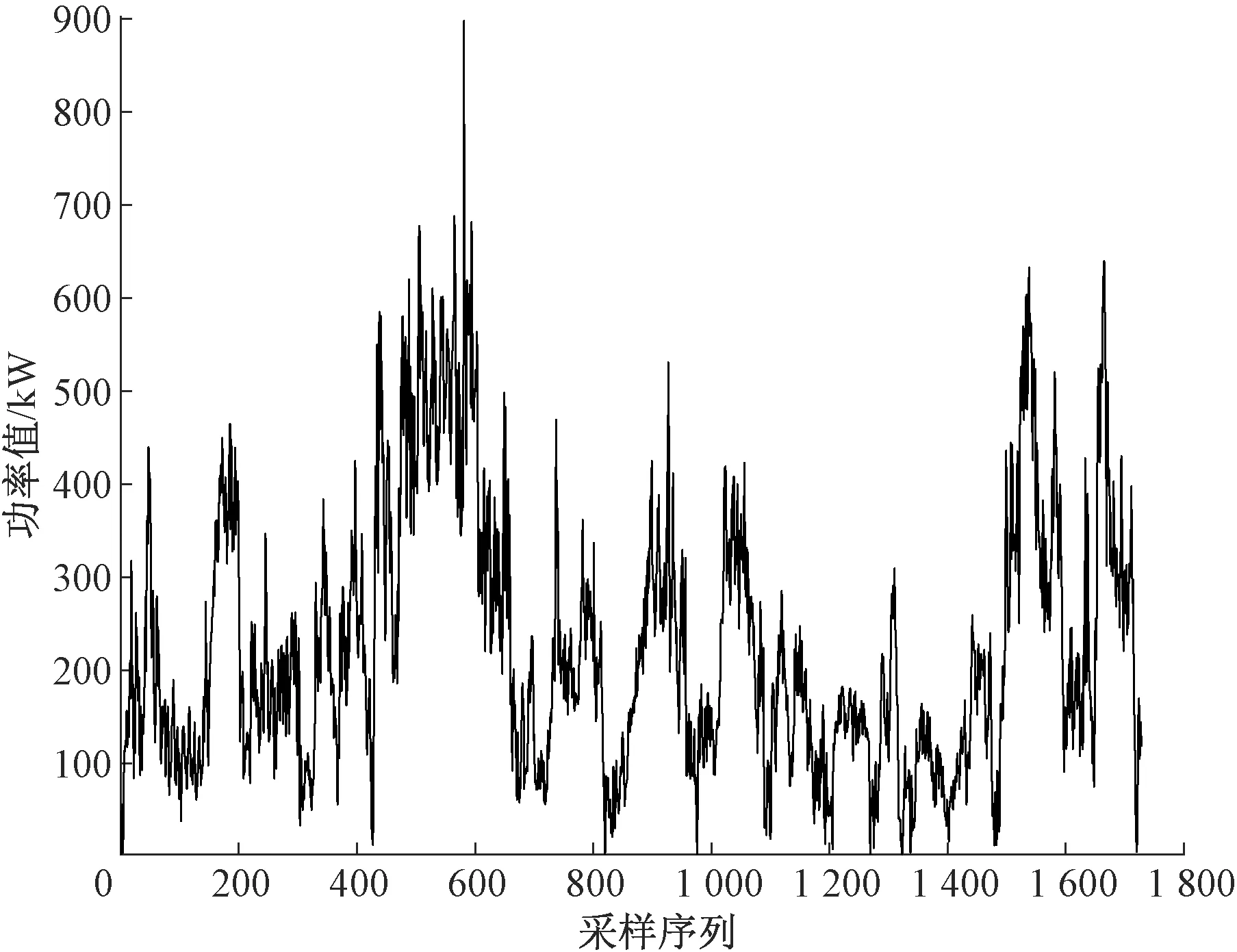
图6 原始数据Figure 6 Raw data

图7 各预测模型的效果Figure 7 The effect of each prediction model

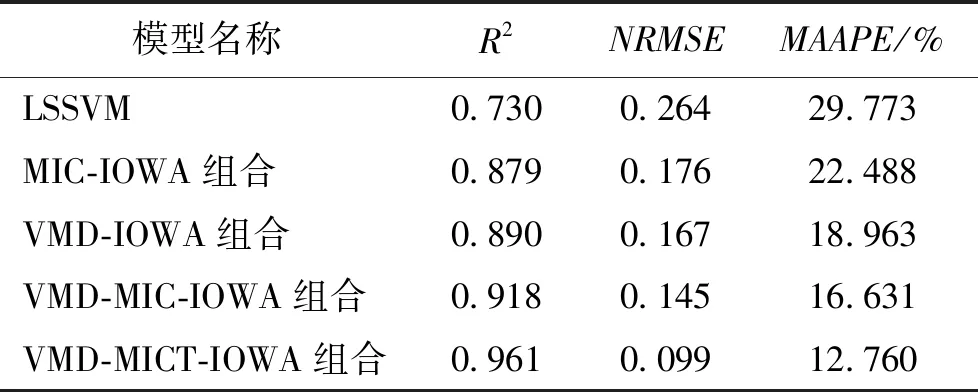
表4 各预测模型的评价指标Table 4 Evaluation index of each prediction model

5 结束语

本文通过分析风电场SCADA系统的数据特征，利用VMD方法将风电功率信号分解为不同频率的分量；基于带时间尺度的MIC进行特征关系的分析，分项单独建立IOWA组合预测模型，叠加各分量的预测结果得到最终的功率预测值。由于考虑了风电功率与特征参量及时序之间的关联性，提高了预测精度。经风电场监测数据研究表明：

1)通过变分模态分解将风电功率序列分解为一系列尺度不同的IMF分量，使用MIC选择特征因素弥补分解过程中的信息缺失；

2)通过考虑不同变量的数据分布特点，结合GRU与LSSVM的优势，建立基于IOWA算子的组合预测模型，提高了整体模型的预测性能；

3)考虑风机的运行条件对能量转换过程有影响，建立综合气象信息和运行条件的多变量信息的组合预测模型，构建多输入-单输出的功率预测模型。

论文下一步的工作重点是在大数据的条件下，对不同的自然风和环境情况进行分类，选择出每类的代表性风机，探索更大时空尺度下的风电场预测方法。