基于最大匹配的移动众包任务分配研究

徐巧枝，张俊星

(1.内蒙古师范大学 计算机科学技术学院 内蒙古自治区 呼和浩特 010022；2.内蒙古大学 计算机学院 内蒙古自治区 呼和浩特 010020)

0 引言

文献[1]设计的雾计算实验平台piFogBedII，通过引入移动众包资源，解决了雾计算实验平台中用户层设备的多样性和移动性问题，保证了实验结果的真实性。

移动众包实验任务分配是piFogBedII平台正常运转的基础，是必须解决的关键问题之一。很多现有移动众包任务分配机制未考虑移动用户偏好[2-10]，只是假设其会执行被分配任务，但这不符合实际，不考虑用户偏好的任务分配会降低任务执行度。

基于拍卖理论的任务分配考虑用户偏好，更符合用户意愿，任务被执行的概率也更高。但现有的基于拍卖的任务分配机制大多以收益最大化为目标[11-19]，并不适用piFogBedII。piFogBedII的目标是基于任务预算，在满足平台和用户非负收益的前提下，使任务匹配数最大。因此，本文基于双向拍卖机制，设计了基于最大匹配的任务(maximal task matching，MTM)分配算法，以任务匹配数最大化为目标，同时兼顾移动用户的偏好。实验结果表明，该算法在任务匹配数上有很大提高，尤其当移动用户相对较少时，可以将任务更均匀地匹配到多个用户。同时，该算法满足诚实性、个体理性和预算平衡性。

1 相关研究

双向拍卖是任务分配机制中经常使用的拍卖模型，可使整体社会收益在买卖双方之间更公平地分配，缓解一方垄断的现象。现有双向拍卖机制大都基于McAfee机制[20]，该机制满足诚实性、个体理性和预算平衡性。

1.1 平衡匹配算法

平衡匹配(equilibrium matching，EM)算法[21]是McAfee机制的经典实现，目标是利润最大化，共包括3个步骤。

1)将卖家的要价非降序排列，将买家的出价非增序排列，

b′1≤b′2≤…≤b′m，

b1≥b2≥…≥bn，

其中：b′i(i∈[1,m])表示卖家的要价；bj(j∈[1,n])表示买家的出价；m、n分别表示卖家与买家的数目。

2)在排序队列中找到满足条件b′k≤bk的最大k值，那么前k-1个买家和卖家就是拍卖的获胜者。

3)向所有获胜的买家收取的费用为第k个买家的出价bk；向所有卖家支付的报酬，为第k个卖家的要价b′k。

1.2 最大匹配算法

文献[21]扩展了EM算法，提出最大匹配(maximal matching，MM)算法，可使交易数最大。MM算法包括5个步骤。

1)给定一组买方和卖方的竞价和要价，用EM算法计算匹配集，将所有已匹配的标记为匹配，其他标记为未匹配；

2)递归检查，如果输入的是已匹配的要价和未匹配的竞价，计算MM得到的匹配数；

3)递归检查，如果输入的是未匹配的要价和已匹配的竞价，计算MM得到的匹配数；

4)选择2)和3)中的最小值作为MM算法可以获得的额外匹配数；

5)将4)中得到的额外匹配集与1)中得到的匹配集交叉，第一个匹配对中的要价与最后一个额外匹配对的竞价重新匹配，而该匹配对中的竞价与最后一个匹配对的要价重新匹配，然后第二个匹配对与最后一个额外匹配的要价和竞价重新匹配，依此类推，直到所有额外匹配都匹配为止。

MM算法适合卖家不同、商品相同的拍卖场景，但在piFogBedII中，移动用户的资源(商品)不同，所以，不能直接使用MM算法最大化任务匹配数。因此，本文基于双向拍卖机制，以最大化任务匹配数为目标，提出最大任务匹配算法MTM，并通过一组实验将其与贪婪算法进行了比较，实验结果证明该算法能够使任务匹配数最大。

2 基于最大匹配的众包任务分配机制

为了便于描述，本文将整个时间轴划分为一组连续、等长的时间片τ，在每个时间片，雾节点维护一个待分配任务表，算法目标是将其中的任务匹配到适合的用户，此处限定一个用户在一个时间片只执行一项任务。

2.1 问题建模

在MTM算法中，雾节点是拍卖师，实验任务是买方，以一定预算雇佣移动用户完成任务，移动用户是卖方，拍卖其设备资源的临时使用权。接下来对3个实体进行建模。

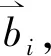
移动用户：假设uj表示当前竞标任务的第j个用户；U={u1,u2,…,um}表示当前竞标任务的m个移动用户。一个用户可同时竞标多个任务，其标书用sj={b′1,j,b′2,j,…,b′n,j}表示。如果b′i,j=0，表示uj不竞标任务ti；如果b′i,j>0，表示用户uj竞标任务ti，且要价为b′i,j。当前时间片所有用户的竞价标书表示为S={s1,s2,…,sm}。

雾节点：收集当前覆盖范围内所有用户的竞价标书，基于各任务预算，计算得到一个可使匹配数最大的任务匹配方案M，然后为移动用户计算报酬。

2.2 算法设计及描述

在时间片τ内，雾节点周边的移动用户是有限的，要使任务分配数最大，就要避免将过多用户集中在某个任务，同时兼顾用户的偏好，满足个体理性、诚实性和预算平衡性。

首先用二分图来描述MTM算法的任务分配过程。设G=(V,E)为无向二分图，其中V表示节点，由用户集Vu与任务集Vt构成，Vu∩Vt=∅。当且仅当用户u对任务t有执行偏好，且u对t的报价不高于其单用户最高报酬时，u、t之间存在一条边eu,t∈E。G中每个任务的度，代表其备选用户数，值越大，表示备选用户越多，如图1所示。

图1 二分图示例Figure 1 Example of bipartite graph

为了满足用户偏好，同时实现任务分配最大化、个体理性、诚实性和预算平衡性，本文将MTM算法分为预分配和调整两个阶段。预分配阶段为任务生成临时的用户匹配集，调整阶段解决用户匹配不均导致的某些任务无用户匹配的问题。

2.2.1任务预分配 预分配阶段为任务生成临时的用户匹配集，包含4个步骤。

1)过滤 piFogBedII中可能会出现任务与用户供求不平衡的现象，为了考虑用户偏好，MTM算法首先过滤无用户竞标的任务，即删除G中度为0的任务。

2)排序 一般来说，度越小的任务对用户的选择性越少，而度较大的任务对用户的可选择性较大。基于这种常识，MTM算法按照度对任务节点非降序排列，优先对度较小的任务分配。

3)匹配 对队列头部的任务t，从G中提取其子图Gt，获得其备选用户集Ut，然后基于McAfee机制，对Ut中的用户按照其要价非降序排列。

EM算法可为任务找到匹配用户，但不会找到最多的匹配用户，MM算法可为任务找到最多的匹配用户，但当用户较少时，可能会将用户集中匹配少数几个任务，导致剩余任务无用户匹配。所以当用户较少时，适合使用EM算法，反之则使用MM算法。MTM算法根据当前时间片内任务与用户的比例μ，确定使用EM或MM。

4)排除 MTM算法中，一个用户可竞标多个任务，但只能被匹配一个任务，所以MTM算法将已匹配用户及其边从图G中删除。

之后对剩余任务的度进行更新，重复执行上述过程。

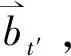
RE算法在一定程度上解决了备选用户相交导致的某些任务无用户匹配的问题。但当用户有限时，仍可能存在一些任务无法匹配到用户，这是无法解决的问题。MTM算法的整体过程如算法1所示。

算法1最大任务匹配算法MTM

输入：用户集U，任务集T及二分图G。

变量：M0为未匹配用户的任务集；M1为匹配到用户的任务集，初始都为空。

输出：匹配集M。

开始

1)预分配阶段

WHILET≠∅

取T中度最小的任务节点→t

IFt.drgee==0 THENt→M0

ELSE

U中与t存在边连接的用户→Ut

对Ut中节点按其要价非降序排列

根据δt构建t的梯度递减出价序列Pt

IF |U|/|T|≥μTHEN MM (Ut,Pt,Mt)

ELSE EM (Ut,Pt,Mt)

IFMt≠∅ THENt→M1;T=T-t

更新T中任务的度并按度非降序排列

END WHILE

2)调整阶段

IFM0≠∅ THEN RE (M0,G,M1)

FOREACHtINM1:M=M∪Mt

RETURNM

结束

FUNCTION RE (M0,G,M1)

FOREACHt′ INM0

IFt′在G中的度为0 THEN CONTINUE

G中与t′存在边连接的用户→Ut′

FOREACHuINUt′

获取u当前所处集合的大小，得到队列L

在L中取元素数最多的集合→M′

IF |M′|>1 THEN

从M′中任选一个用户u∈Ut′，u→Mt′，t′→M1

END RE

2.2.3报酬计算 完成任务匹配后，MTM算法需要为用户计算酬劳。本文假设移动用户不会因为参与任务而改变其移动轨迹，执行同一任务的成本相近，因此MTM算法为参与同一任务的用户支付相同的报酬。

平台通过分配任务获得的收益，等于所有已分配任务向平台支付的费用与平台为用户支付的报酬的差，计算为

其中：N表示成功匹配到用户的任务数；Ps表示实验用户支付的总费用；P′s表示向移动用户支付的总报酬。

由于同一任务的执行者获得同等报酬，都不高于任务出价，平台向实验用户收取的费用不低于其支付的报酬，因此平台的收益是非负的。

2.3 算法分析

本节分析MTM算法的性能和满足的性质。

2.3.1MTM算法的复杂性分析 假设有m个用户，n个任务，用矩阵邻接表存储二分图。从n个任务中寻找度最小的节点，最坏情况下需要进行n次比较，平均时间复杂度为(n+1)/2。获取一个任务节点的子图最多需要m次比较，n个任务节点共需要n×m次比较运算。在调整阶段，最坏的情况是m个用户全部匹配到一个任务，剩余(n-1)个任务均进入M0，那么最多需要进行n×(n+1)/2次调整，所以MTM的时间复杂度为O((n+1)/2+n×m+n×(n+1)/2)，这说明该算法可在多项式时间内求解。

另外，MTM算法运行在雾节点，由于其资源和可覆盖地理范围有限，导致所能部署的实验任务数n及服务的移动用户数m都是有限的，所以本算法可以保证计算高效性。

2.3.2MTM算法满足的性质

性质1MTM使任务匹配数最大。

证明MTM算法在预分配阶段得到的临时匹配集中包含了所有可以匹配任务的用户。如果MTM算法的任务匹配数不是最大，那么至少存在一个任务ti未被匹配到用户，即其匹配集mi为空。根据MTM算法，可分以下几种情况讨论。

1)任务ti的原始子图为空，即没有用户竞价该任务，或者用户竞价均高于其最高支付额，这种情况下，满足预算平衡的算法都不会为该任务分配用户。

2)任务ti的原始子图不为空，且与其他任务无交集。按照MTM算法，原始子图中的节点会被放入任务ti的匹配集mi，那么mi不为空，与前提条件矛盾。

3)任务ti的原始子图不为空且与其他任务有交集。假设任务tj的匹配集mj与ti的原始子图交集不为空，根据MTM算法，只要mj中的用户数不少于2个，就会将相交用户调整到mi，从而减少未匹配任务数。当mj中的用户数小于2个时，不能调整，因为会导致原任务匹配集为空。对每个未匹配任务执行调整操作，最终使得能够匹配的任务均匹配到用户，可使任务分配数最大。证毕。

性质2MTM满足预算平衡性。

性质3MTM满足个体理性和诚实性。

证明MTM算法的报酬和费用计算沿用了McAfee机制，McAfee机制满足个体理性和诚实性，所以MTM算法也满足个体理性和诚实性。证毕。

3 实验评估

目前基于双向拍卖机制对移动众包任务进行分配的研究，目标大多是收益最大化，与本文的目标不同，无法直接比较，因此，实验中将MTM算法与贪心算法进行了比较，验证MTM算法在任务分配数方面的有效性。实验假设，贪心算法基于任务的预算和最大单笔支付额度，贪婪地将任务分配给竞标用户，并将所有胜出用户的竞价平均值作为完成该任务的报酬。

激励用户的积极性是众包系统持续发展的源动力，在分配任务时，应尽可能让更多诚实的用户有机会被分配到任务。为了达到这个目的，MTM分别在用户数较多和较少时，使用了MM与EM算法，验证了对用户参与度的影响。

本文比较了MTM算法与贪心算法的运行效率，证明了MTM算法的有效性。

3.1 任务分配数比较

本实验测试当用户数分别为4、20，待分配任务数分别为2、4、6、8、10时，MTM算法与贪心算法的最终任务分配数。实验中，各个任务的主要参数利用随机函数生成，假设每个任务的预算为[10,20]，每个任务的最大单笔支付额为[2,5]，各用户的竞价为[0,6]，并且所有任务的价格递减梯度均相同，即δ=0.5，μ=2。为了获得更具一般性的结果，本实验将两种算法各运行100次，并计算平均分配的任务数，实验结果如图2所示。

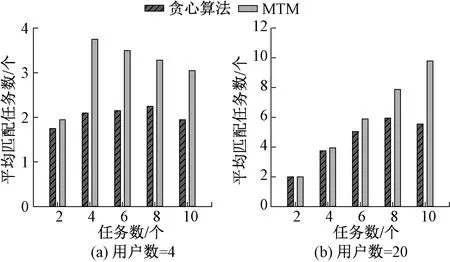
图2 MTM与贪心算法的平均分配任务数比较Figure 2 Comparison of MTM and greedy algorithm in average number of task allocation

实验假设只要被分配任务，用户就会执行，所以只要任务被匹配了至少一个用户，就认为其被成功分配。从图中可以看出，当用户数一定时，MTM算法的平均任务分配数高于贪心算法，主要原因是MTM算法与贪心算法相比，并不是将竞标且满足预算的用户全部分配给该任务，而是通过EM或MM算法，只选择其中一部分用户，这就为其他任务预留了部分用户。另外，在MTM算法的调整阶段，对未分配到用户的任务进行了调整，进一步提高了任务被成功匹配的数目。

3.2 EM与MM匹配的用户数

图3 EM和MM算法对用户匹配数的影响Figure 3 Influence of EM and MM on user matching number

3.3 MTM与贪心算法的效率比较

最后，实验测试了MTM与贪心算法在不同用户数、任务数时的运行效率，结果如图4所示。考虑一个雾节点上可能部署的最大任务数及周边可能参与任务的移动用户数，实验设置用户数为100和300，任务数为20、40、60、80和100。为了使任务能够得到最大程度的匹配，设置所有任务的预算为1 000元，每个任务的最高支付额度在0.5～2元随机变动，用户的竞价在0～2元随机变化，设置价格梯度下降值δ=0.1。

图4 MTM算法与贪心算法的运行效率比较Figure 4 Efficiency comparison between MTM algorithm and greedy algorithm

从图4中可以看到，随着用户数和任务数的增加，两种算法的运行时间都会增长，MTM的增长幅度更大，这是因为贪心算法判断用户竞价满足条件后，即将任务分配给用户，而MTM会运行EM和MM算法，对用户的出价进行排序，对未匹配用户的任务进行调整等，导致运行时间增加。但是从实验结果来看，当用户数为300，任务数为100时，MTM算法的平均运行时间大约为22.4 ms，这个时间长度对于移动用户是可接受的。

另外，由于可用资源和覆盖范围的限制，一个雾节点上所部署的任务往往不会很多，在同一时间片内参与竞标的用户也不会很多，所以任务分配的实际运行时间应该更短。虽然MTM算法比贪心算法的运行时间长，但是在用户可接受范围内，获得了贪心算法所不具备的诚实性和个体理性，这些特性对于拍卖系统来说是非常重要的，对于维护众包系统的长期健康运转是非常关键的。

4 总结

piFogBedII是一个雾计算测试平台，其任务分配的目标是在短时间内将尽可能多的实验任务匹配到用户，以加快实验用户的进度，这就决定了它不能以收益最大化为目标，而是要以任务分配数最大化为目标。为了实现这个目标，本文基于双向拍卖机制，提出了最大任务匹配算法MTM，并从理论和实验两方面对该算法进行了分析和验证，结果表明，MTM算法可使任务匹配数最大，并满足双向拍卖的诚实性、个体理性和预算平衡性。