基于有限元的双铣头龙门机床设计优化

李再参，邓 琎

（云南省机械研究设计院，云南省机电一体化应用技术重点实验室，云南 昆明 650031）

0 引言

机床在切削加工过程中，要承受各种外力的作用，承受的静态力有运动部件和被加工零件的自重，承受的动态力有：切削力、驱动力、加减速时引起的惯性力、摩擦阻力等。机床的结构部件在这些力作用下，将产生变形，变形量的大小用机床刚度系数来衡量。静力引起的变形为静刚度，是导致工件的加工误差产生的主要因素之一。动载荷引起的变形为动刚度，其主要影响机床切削过程的特性，比如振动，工件的表面质量等。

近年来，随着有限元理论的成熟和计算机技术的快速发展，有限元技术应用于辅助机械设计越来越广泛。在机械产品研发阶段，应用有限元技术对机械结构初步设计进行仿真计算，评估结构的强度、静刚度甚至动刚度，可以提高设计的准确性和可靠性，节省样机研发周期，降低研发成本。本文针对某型双铣头龙门铣床，在设计时对机床处于切削力闭环系统中的主要结构件组成进行静刚度有限元分析，预评估设计刚度并寻找结构刚度的薄弱环节，进行改进，从而提升机床的总体静刚度。

1 机床结构及典型工况条件受力分析

龙门铣床的结构形式见图1，其组成的主要零部件为：桥墩、导轨（滑道）、主轴座（滑块）、横梁和丝杠。工作台、床身和主轴、主轴箱为成熟借用件，此次不作设计分析计算。

图1 龙门铣床的结构形式Fig.1 Structure of gantry milling machine

龙门铣床为铣削加工，本分析考虑机床在典型工况条件下的极限载荷以静载荷形式施加。主要为铣削条件下的切削力及机床大件的自身重力。根据对刀具和铣削加工运动的影响，作用在铣刀刀齿上的铣削力可分为沿铣刀圆周方向的切削力FX、沿铣刀半径方向的径向力FY及沿铣刀轴线方向的分力FZ。

切削力的计算：

依据《机床设计手册》，铣削时的圆周切削力PZ和铣削功率N的关系为：

式中：V—切削速度；N—铣削功率，取为主电机运作最大功率，N=15kW。

最小切削速度为：

V=πDn

式中：D—铣刀直径；n—主轴输出转速。

根据选装铣头《U12输出转矩表》，取D=250mm，nmin。故

V=π×0.25×66=51.8m/min

所以

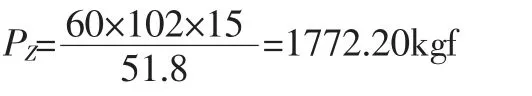
P=PZ×g=17367.56N≈17370N

根据《【机械行业标准】JBT 3029-1993龙门铣床 技术条件 标准》，对于机床的切削抗力实验，切削刀具采用端铣刀，试件材料采用灰铸铁。查找《切削力计算》，端面铣刀有一下三种铣削方式：

对 称 铣 削：PH=（0.3-0.4）PZ，PV=（0.85-0.95）PZ，P0=（0.5-0.55）PZ。

不 对 称 逆 铣：PH=（0.6-0.9）PZ，PV=（0.45-0.7）PZ，P0=（0.5-0.55）PZ。

不 对 称 顺 铣：PH=（0.15-0.3）PZ，PV=（0.9-1.0）PZ，P0=（0.5-0.55）PZ。

将其与Ansys中坐标系相比较（PV↔FZ，PH↔FX，P0↔FY），并取各个方向力的最大值：

对 称 铣 削：FX=0.4P=6948N，FZ=0.95P=16502N，FY=0.55P=9554N。

不对称逆铣：FX=0.9P=15633N，FZ=0.7P=12159N，FY=0.55P=9554N。

不 对 称 顺 铣：FX=0.3P=5211N，FZ=P=17370N，FY=0.55P=9554N。

值得注意的是，在与刀头平行的方向上（即Y向），只存在竖直向上的力。而在与刀头垂直的平面上，存在两个方向上的力（X向和Z向）。这两个力的方向根据机床刀头的移动方向以及工件在传送带上的移动方向，而各有正负。因此，Y轴上的力只能是正方向，而X和Z轴的方向均存在正负。故对每种切削方式存在4种力的施加方式，即总共12种工况（注：坐标系参考可见图1）。

（1）有限元模型建立。几何模型为Solid works生成的模型，将装配体调整到工作极限位置，输出.x_t格式，导入有限元软件进行前处理。

材料参数如表1所示。其中两丝杠和两滑道采用Q235钢，其余部件均采用HT250材料。

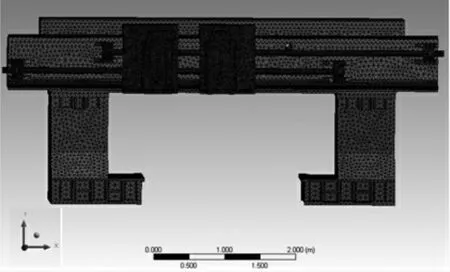
图2 有限元模型Fig.2 Finite element model

表1 材料参数表Tab.1 Material parameter table

（2）位移边界条件和载荷施加。在相应位置实加载荷和重力。切削力实加在刀头位置，位于坐标（-0.1，1，0.7）出，通过设定远端点，将远端力作用于远端点的方式来进行添加，见图3。

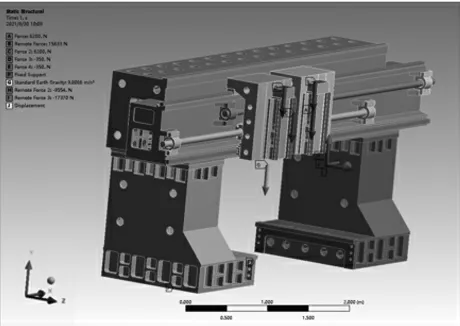
图3 边界条件和载荷施加Fig.3 Boundary conditions and load application

底部两侧面为固定约束，而与地面接触的两底面则约束其Y方向的位移为0。

2 接触设置

对于接触方式的设置，除两滑道与两滑块相接触位置采用有摩擦接触，摩擦系数为0.08外，其余部件的接触均采用绑定（即看作一个整体）。除此之外，如果切削力在z轴方向上的分力是沿着正方向的，那么为了防止脱轨，滑道2与滑块1的接触在这种情况下使用不分离接触。

3 结果分析

结果有限元计算后，变形以及远端点处位移见图4。

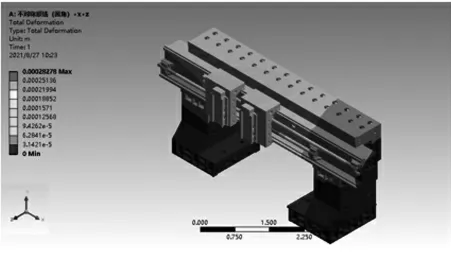
图4 有限元计算变形云图Fig.4 Calculated deformation of structural

12种工况下分别计算后的最大应力和最大位移结果见表2。

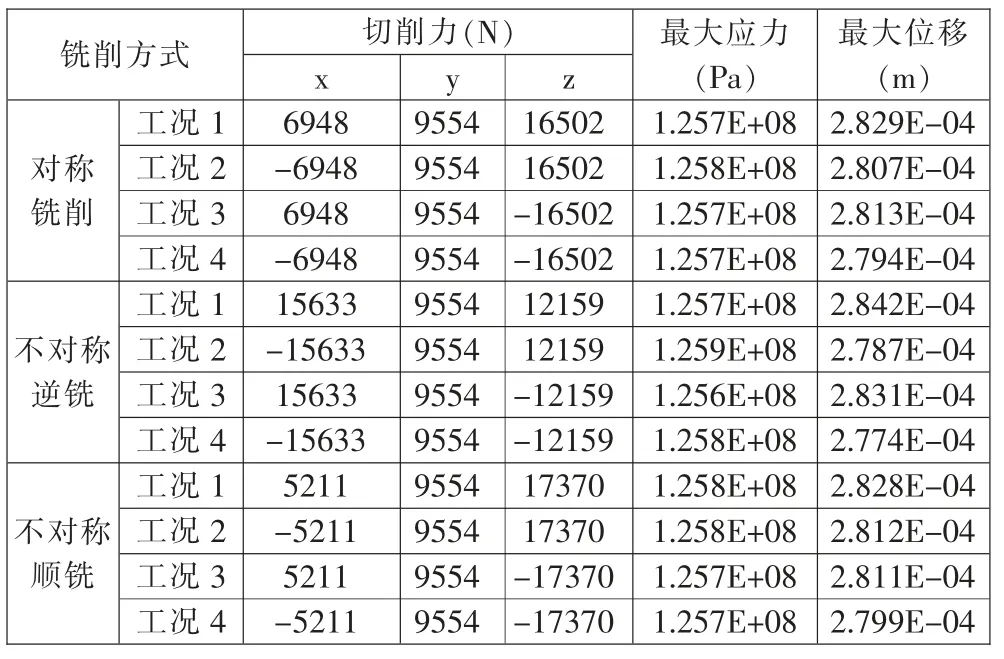
表2 不同工况下的最大应力和最大位移Tab.2 Maximum stress and displacement of different working conditions

12种工况下分别计算后的远端点位移和静刚度结果见表3。

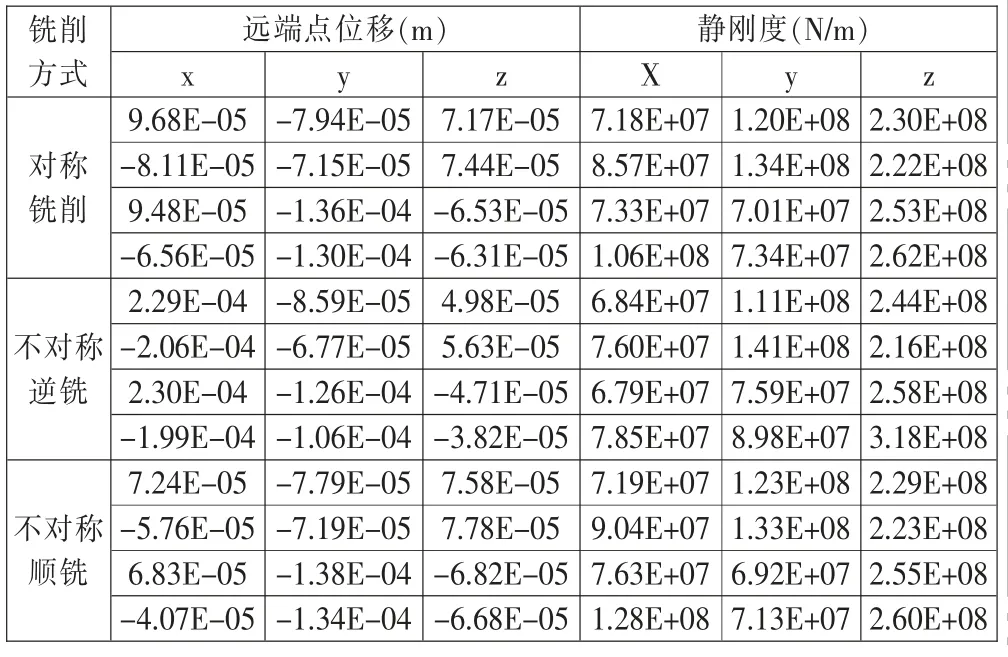
表3 不同工况下远端点位移和静刚度结果Tab.3 Displacement and static stiffness of different working conditions

计算结果表明：向最小刚度为X向106N/um；Y向120N/um；Z向为216N/um。由于没有相关标准针对龙门铣床规定静刚度要求，本文参考中国机械行业标准JB/T 2800.3—2011《升降台铣床 第3部分：静刚度》的要求：对于升降台铣床其各向刚度为40 N/um，本设计静刚度以最小X向刚度计算，达到标准要求的2.5倍。

本设计的静刚度虽然满足要求，但通过观察应力云图，排除应力奇异，发现滑座局部应力相对较大，见图5、图6，为机床静刚度薄弱环节，在不大幅增加制造成本的前提下，尚可进行改善。具体改进建议：为使结构达到均衡的应力分布，适当加厚局部铸件筋板的厚度，见图7，主要考虑：①铣头底座筋的壁厚加厚；②下导轨安装处作适当加强处理。

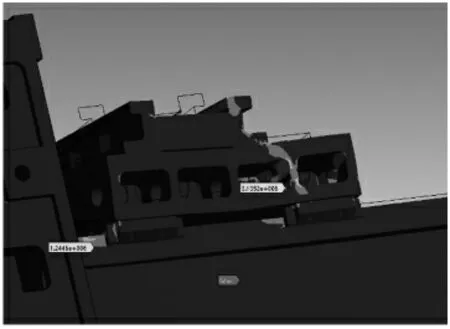
图5 铣头底座筋壁厚应力云图Fig.5 Stress cloud map of rib

图6 下导轨安装处应力云图Fig.6 Stress cloud map at the guide rail

图7 横梁改进示意图Fig.7 Improvement diagram of beam

4 结论

对初步设计的龙门铣床的立柱、横梁、主轴座和主轴箱记性了静刚度有限元分析，结果表明该机床X，Y，Z向的刚度均满足设计要求。

根据应力分布云图，找到变形较大的零件和刚度薄弱环节，针对零件结构提出低成本改进建议。