基于圆柱绕流分析k-ε和k-w湍流模型的差异

王亚龙，朱潇潇

（航天工程大学，北京 101416）

0 引言

随着计算机技术的普及和计算方法的发展。作为计算流体力学和计算传热学的新型研究方法，CFD技术得到了迅猛发展。因为相对于实验研究，数值模拟有很多独特的优点。例如：成本低、周期短以及能获得较为完整的数据。同时能够模拟出实际运行过程中的各种测试数据。对于新产品的研发设计和改造有着重要的指导作用。所以，目前CFD技术不仅在电子，制冷等实际工程领域中的应用越来越广泛。在现代航空航天、核能工程等领域里的应用也越发的广泛与深入。首先，商业CFD软件数值模拟功能是强大的，它是目前功能最全面适用性最广使用最广泛的流体软件之一。是基于CFD软件群思想，从用户需求角度出发，针对各种复杂流动的物理现象所采用的数值解法。从而能够在计算速度稳定性和监督等方面达到优化组合[1]，高效的解决各个领域的复杂流动计算问题；模拟流动传热和化学反应等诸多物理现象。它能够提供非常灵活的网络特性。让使用者可以使用非结构网格，包括三角形、四边形、六面体、金字塔型网格以及混合型非结构网格[2]，并允许用户根据求解的具体情况对网格进行修改。包括对网格的细化和粗化，从而解决具有复杂几何形状的流动换热问题。CFD已经成为流体数值模拟过程的一种重要的手段，然而，湍流是著名的难题，湍流是相对于层流来说的，流体的层流被看作是比较平滑的流动，而湍流无论是在空间还是在时间域内都是无规则的运动。这一定义是1883年由Reynolds实验时发现并一直沿用至今，实验研究在湍流研究中占有十分重要的地位[3]，从湍流的发现，层流到湍流的过渡，湍流拟序结构的发现和研究都与实验密切相关，同时湍流理论研究进展也积极推动着湍流实验研究的深入。如20～30年代的各种湍流理论，如Prandtl动量输运和Taylor的涡量输运理论，以及后来的Karman相似理论为湍能的产生和耗散之间的平衡关系的实验研究起了指导性作用。近年来对拟序结构的研究进一步揭示了湍流内在的一些重要机理，如湍流的扩散和发展不仅仅是小尺度涡旋随机扩散的结果，更主要是由大尺度拟序结构的相互作用和卷并所致[4]。由于流现象广泛存在于自然界和工程技术的各个领域，因此湍流基础理论研究取得的进展就可能为经济建设和国防建设的广泛领域带来难以估量的效益。尽管湍流研究相当困难，但是仍然有大量的国内外学者致力于这一领域的工作。目前随着计算机技术和测量技术的不断发展，湍流的精细实验正在进一步地展开，它对深入认识湍流的物理本质至关重要[5]；相关学科的发展也推动了湍流的研究，经过很多科研人员的研究，结果表明：选择合适的湍流模型对于研究结果的合理性和正确性极为重要，本文基于CFD软件分析了二维圆管流道内的圆柱绕流问题。通过选取k-w和k-ε湍流模型，分析了两种湍流模型在计算圆柱绕流时的差异。

1 算例的选用

1.1 研究状况

一个世纪以来，圆柱绕流一直是众多理论分析、实验研究及数值模拟对象。但迄今对该流动现象物理本质的理解仍是不完整的。圆柱绕流中，起决定作用的是雷诺数，但还受到许多因素，如阻塞比，来流湍流度，下游边界条件等的影响[6]。随着雷诺数的增加，粘性不可压缩流体绕圆柱的流动会呈现各种不同的流动状态，在小雷诺数时，流动是定常的，随着雷诺数的增加，圆柱后会出现一对尾涡。当雷诺数较大时，尾流首先失稳，出现周期性的振荡。而后附着涡交替脱落，泻入尾流形成Karman涡街，随着雷诺数的增加，流动变得越来越复杂，最后发展为湍流[7]。

一般认为圆柱绕流有2种定常的流动图案：雷诺数为较小时，圆柱后无尾涡；当雷诺数为较大时，圆柱后有一对对称的尾涡。关于定常流失稳以及出现湍流的临界雷诺数主要是通过应用流场显示技术观察流动形态得到的，所以不是准确值[8]。

圆柱周围的强制对流传热在工程中有许多应用，例如燃气轮机冷却，热交换器，核燃料棒等。圆柱或其他形状的圆柱的传热增强和错流引起了研究人员的充分关注。Buyruk等对雷诺数为120和390的错流圆柱流的层流和传热特性进行了数值和实验研究[9]。对于390的雷诺数，与实验相比，他们通过数值计算获得了更好的预测结果。力由Hover等人测量。在跨度为60cm的刚性圆柱体的两端，在进入的水流中在Re处执行横向振荡。Catalano等研究了大涡模拟（LES）的可行性和精度，并考虑了在超临界状态下考虑圆柱体绕流的高雷诺数复杂湍流。但是，没有捕获雷诺数依赖性，并且随着雷诺数的增加，解决方案的准确性降低[10]。Bouhairie和Chup使用二维模型研究了从圆柱表面到横流的传热，其雷诺数范围从Re=200到15550。结果表明，二维模型捕获了不稳定过程并产生了与可用实验数据一致的结果[11]。它提供了相对正确的总体结果，前停滞和总传热速率。Patnana等研究在二维（2-D）非定常流动状态下，将a浸没在流动的幂律流体中的圆柱体的强制对流传热特性。根据他们的研究，无论流动行为指数如何，努塞尔数都随着雷诺数或普朗特数的增加而增加[12]。Khan等使用Karman-Pohlhausen方法研究了无限圆柱周围的流体流动和热量传递。阻力系数和传热系数的结果与圆柱的实验/数值数据非常吻合[13]。

1.2 几何模型及数值方法

1.2.1 几何模型

如图1所示，计算域为二维等直圆管，中间为圆柱绕流体，圆柱直径D为20mm。为有效捕捉涡脱落过程，在圆柱周围和壁面都进行了网格加密，网格总数为9万，最小网格尺寸为0.4mm，壁面边界层y+＜1。管内流体为自定义气体，由于流速较低考虑气体为不可压流体，密度ρ为1kg/m3，动力粘度为μ=0.00025Pa·s。为保证流动为充分发展的湍流，如图2所示，在入口根据式（1）利用UDF定义充分发展的湍流。当雷诺数Re为800时，圆管入口流速为1m/s；雷诺数Re为8000时，管的入口速度为10m/s。

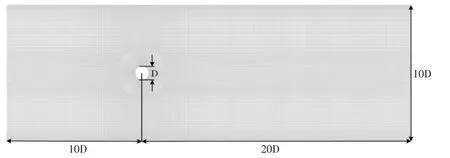
图1 几何模型及计算域网格

式中：Umax—气体最大流速；Dinlet—圆管入口直径；y—纵向坐标。边界条件如图2所示，气体为不可压粘性流体，因此入口为速度入口，出口为压力出口，流道内圆柱和圆管壁面均为无滑移绝热壁面。

图2 入口速度分布及边界条件

1.2.2 数值方法

本文中，不可压粘性流体的控制方程包含连续性方程和动量方程

连续性方程：

动量方程：

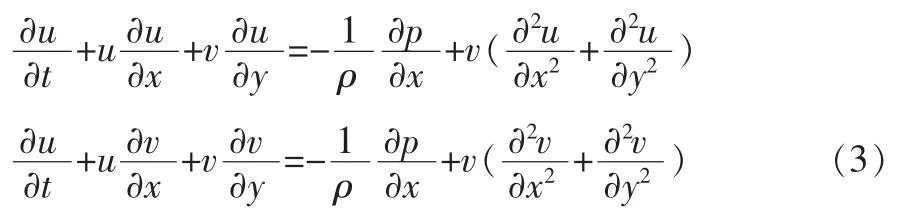
升力系数Cd定义为：

斯特劳哈尔数St是振荡流的无量纲度量，其定义如下：

式中：f—涡脱落的频率；L—特征长度，本文中为流场中圆柱直径，U是来流速度。理论指出在800＜Re＜20000时St数几乎不变为0.2。通过计算St数并与理论值进行比对，比较不同湍流模型对涡脱的捕捉能力。

本文中采用PISO算法求解压力速度耦合，压力项采用PRESTO！离散。方程中的对流项采用二阶迎风差分格式来离散。为提高计算精度动量方程的离散采用了QUICK格式；瞬态方程采用了二阶隐式离散以提高涡脱落的捕捉能力[14]。

2 结果与讨论

2.1 网格无关性验证

基于k-w模型，在雷诺数为8000时进行了网格无关性验证。通过监测圆柱表面升力系数的变化来表示涡脱落过程。对升力系数进行快速傅里叶变换从而得到涡脱落频率。在三种尺寸的网格上进行了计算。网格数量分别为2万、9万和30万，见图3。

图3 三种网格尺寸下的涡脱落频率

根据公式（5）计算出St数，见表1。

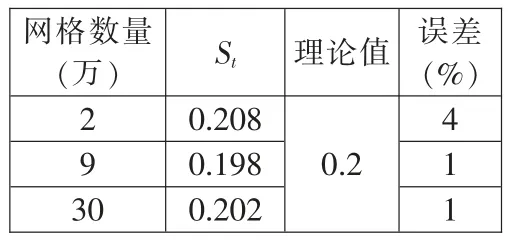
表1 不同网格下的St数与理论误差

通过比较可以看出，网格在9万和30万时误差较小，并且网格从9万增加到30时频率变化不足1%。考虑计算资源的限制，选取数量为9万的网格进行计算。

2.2 k-w模型和k-ε模型的对比

当雷诺数为8000时，比较 了k-w和k-ε模型 在计算圆柱绕流时的差异。如图4 所示为不同湍流模型下的流场，可以看出在使用k-ε模型计算时，圆柱后方存在较大区域的低速回流区，在向下游流动的过程中流场震荡迅速衰减，流线较为平稳。而k-w模型在捕捉雷诺数较高时捕捉到的涡的尺寸较小，但能够捕捉到逐渐向下游衰减脱落的过程，流场震荡幅值较大。

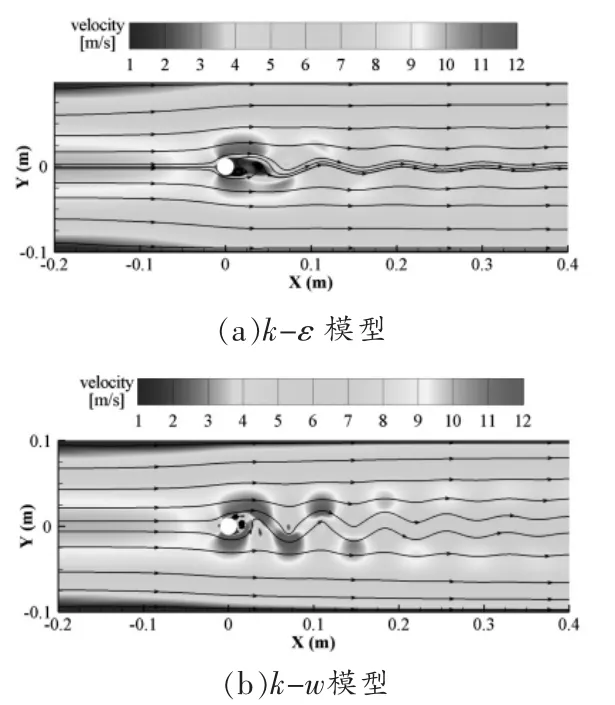
图4 不同湍流模型下的流场

图5 显示了不同湍流模型下的涡量场，可以看出两种模型在涡量的捕捉上存在巨大差异，k-w模型明显更能精确地捕捉到涡量，而k-ε模型存在着严重的失真。k-ε模型计算的涡量严重偏小，说明此模型流场外围涡的捕捉能力不强。

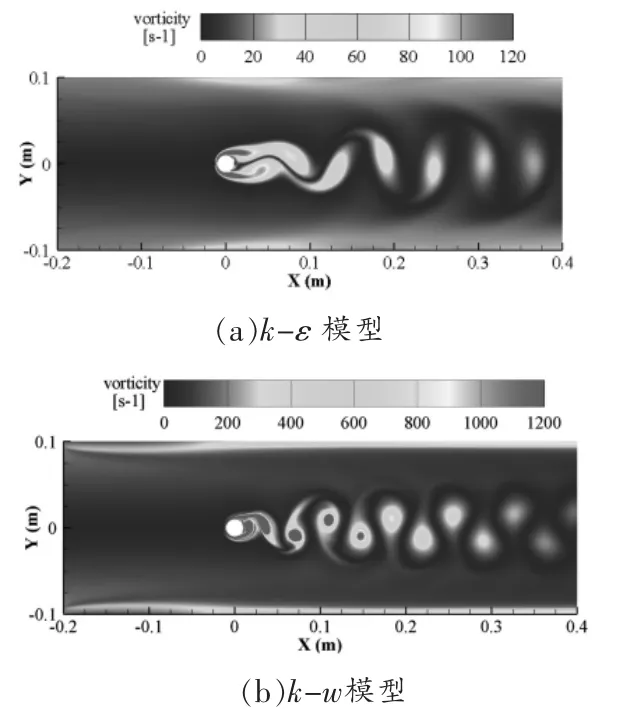
图5 不同湍流模型下的涡量场

图6 显示了涡脱落的幅频图，从中可以看出用k-ε模型计算的涡脱落频率为81Hz，而k-w模型计算的为99Hz，对应的St数分别为0.162和0.198。与理论值0.2相比k-ε模型误差较大，说明k-ε模型不适应于圆柱绕流的仿真。

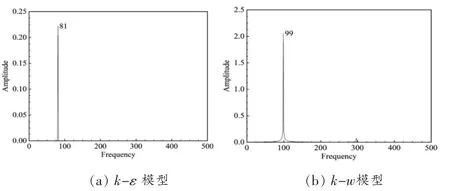
图6 不同湍流模型下的频谱图

2.3 与k-ε、k-w湍流模型对雷诺数的响应

为研究雷诺数对湍流模型的影响，分别计算了雷诺数为800和8000时的圆柱绕流案例。图7和图8分别是不同雷诺数下k-w模型与k-ε模型的涡量图。可以看出随着雷诺数的增加涡量增加，但k-w模型在雷诺数为800时依然能够清晰地捕捉到涡脱落，而k-ε模型在低雷诺数时涡量趋于稳定，没有明显的涡脱落行为，整个流场变成稳态。说明k-ε模型对低雷诺数流动不敏感，没能成功捕捉到低雷诺数下的涡脱落行为。

比较图7（a）和图8（b）可以看出，在雷诺数为800时利用k-w模型捕捉的涡量场与雷诺数为8000时用k-ε捕捉的涡量场十分相似，涡量的强度也相差不大，这说明k-ε模型只有在雷诺数达到一定程度后才能捕捉到涡脱落，且涡量强度误差较大。由此可以推测k-ε模型可能更适应于高雷诺数流动。

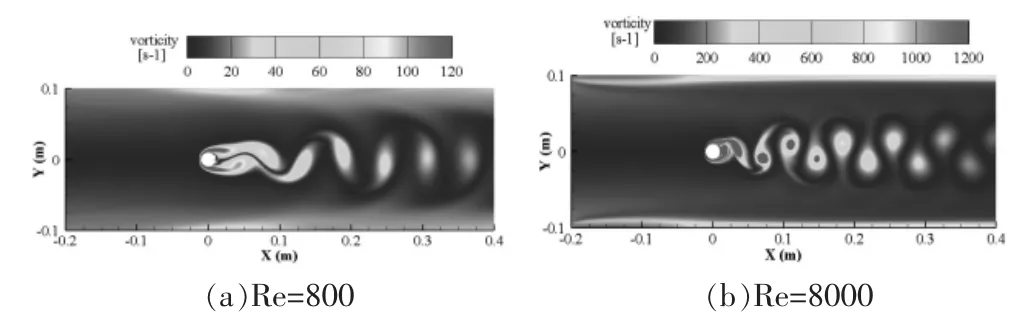
图7 k-w模型对雷诺数响应的涡量图

图8 k-ε模型对雷诺数响应的涡量图

2.4 定常与非定常k-w模型的区别

为研究定常与非定常k-w模型在计算圆柱绕流时的差异，在雷诺数为800时，分别使用稳态和瞬态的k-w模型进行了圆柱绕流的仿真。如图9所示显示了雷诺数为800时定常与非定常k-w模型的涡量场，可以看出即使流动为层流，流场中依然存在非定常的涡脱落行为。在用定常计算时流场迅速收敛达到稳态，无法捕捉到涡脱落这种瞬态行为，而非定常k-w模型即使在雷诺数较低的情况下也能捕捉到涡脱落行为。

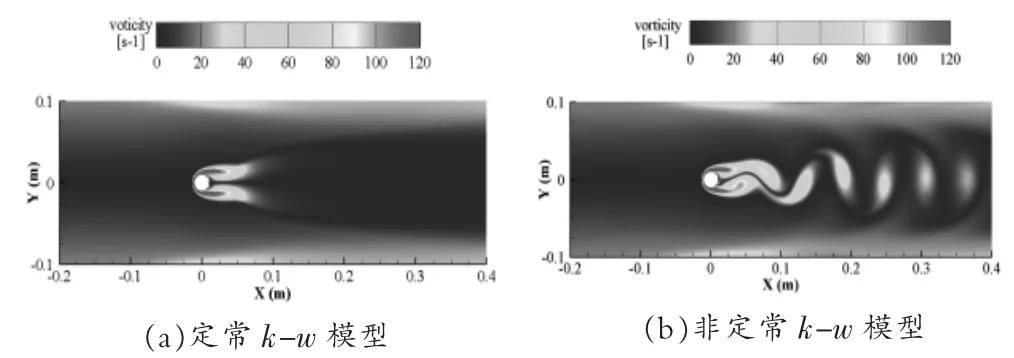
图9 定常与非定常模k-w型涡量场

3 结论

本文基于CFD软件，分别选择在k-ε和k-w模型下对圆柱绕流问题进行了数值模拟。首先验证了网格无关性，然后模拟了两种不同模型下的涡脱落频率和流场云图。比较了两种湍流模型对不同雷诺数的响应。得出结论如下：

通过监测圆柱表面的升力系数，得到了涡脱落频率，发现Re=8000时k-w模型能够有效捕捉涡脱落，对应的St数为0.198与理论值吻合良好。采用k-ε模型计算圆柱绕流误差较大。

对比了不同雷诺数下k-ε和k-w模型涡脱落的捕捉能力，发现在雷诺数低于一定值后k-ε没能捕捉到涡脱落行为，说明k-ε模型不适合低雷诺数流动。

涡脱落为瞬态过程，对比稳态和瞬态的k-w模型，发现在稳态计算时流场趋于稳定，定常k-w模型没能捕捉到涡脱落的过程。