数字体图像相关方法的亚体素算法性能研究

代延辉，许 蔚，李 坤

（昆明理工大学 建筑工程学院，云南 昆明 650500）

0 引 言

如何精准获得材料的力学性能始终是当今研究的热点问题之一，根本原因在于无法准确测量其内部变形，传统的测量方法（如应变片法、散斑干涉法、光弹性法等）具有一定的局限性，导致测量结果与实际变形相差甚大。近年来，随着三维层析设备与计算机图像处理技术的成熟，许多新型测量技术喷涌而现，最具代表性的是数字体图像相关方法（Digital Volume Correlation，DVC）。数字体图像相关方法是一种有效的光学测量技术，具有无损性、抗干扰能力强、测量范围广等多种优势，广泛地应用于生物医学、实验力学和材料科学等多学科交叉领域。

数字体图像相关方法通过对比变形前后物体图像的位置变化，以获取其内部的变形场信息。该方法在计算过程中通常分为如下两步，即整体素位移搜索和亚体素位移测量。整体素位移搜索可采用空域或频域搜索以获得物体内部的位移，然而该方式测得的位移精度不足以达到预期理想，因此需要采用亚体素位移算法进一步提高测量精度。亚体素位移测量算法是将整体素搜索的位移初值不断进行优化直至达到亚体素精度，是提高测量精度的关键性技术，对此研究人员先后提出拟合算法、灰度梯度算法、前向累加牛顿-拉弗森（FA-NR）算法以及三维反向高斯-牛顿（IC-GN）算法等多种算法用于实现亚体素位移的测量。基于不同类型的算法，其测量精度和计算效率各不相同，如何选取最佳算法尤为重要，因此定量对比多种算法的计算性能具有十分重要的指导意义。

本文介绍了在数字体图像相关方法中最为常见的三种亚体素位移测量算法，通过计算机模拟三维散斑体图像的刚体平移实验，对比不同算法的测量精度和计算效率，随后利用椎骨零应变原位扫描实验进一步对比三种算法的测量误差，实验均表明IC-GN算法的性能最优。

1 数字体图像相关方法的基本原理

采用数字体图像相关方法测量物体内部变形时，需要结合三维层析设备记录测试对象在不同状态下的体图像，通过匹配技术寻找这些图像中灰度相同或相似的体素点，对比该点在变形前后位置的变化以获取物体内部变形场信息。具体步骤如下：首先在变形前的体图像中选取一个尺寸为(2+1)voxel×(2+1)voxel×(2+1)voxel的正方体为参考子体块，通过搜索寻找变形图像中灰度最为相似的目标子体块，并且采用相关系数（如最小平方距离函数、归一化互相关函数等）评价两者的相似程度。由于搜索时只能以体素为单位，该方式测得位移无法达到亚体素级别的精度，因此需要借用亚体素位移算法提高测量精度。

1.1 三元二次多项式拟合算法

数字体图像相关法的拟合算法与二维算法类似，如图1所示。首先通过整体素搜索获得位移初值，选取一个以整体素点为中心、大小为3×3×3的子体块为研究对象，采用三元二次多项式对该点周围的几个离散点进行插值拟合，该多项式极值点对应的坐标便是所求点的位置，进而计算出亚体素位移。

图1 拟合点示意图

三元二次多项式拟合函数为：

式中共有10个未知参数（～），为了求取其对应的数值，通常选取等距的12个离散点依次代入三元二次多项式中，可计算出所有未知量及多项式表达式。拟合获取多项式的极值点应满足下列关系：

最终计算得出的亚体素位移为：

1.2 前向累加牛顿-拉弗森（FA-NR）算法

FA-NR算法是通过逐步非线性迭代优化整体素位移的初值直至收敛到最佳值，其实质是将相关系数求导问题转化为参数求最优值问题。FA-NR算法的基本原理与拟合算法截然不同，需要用一阶形函数描述子体块的形状变化，其定义如下：

式中：(,,)和(′,′,′)分别表示子体块变形前后的中心点；，，为中心点在，，方向上的位移变化量；Δ，Δ，Δ为子体块内一点到中心点的距离；u，u，u，v，v，v，w，w，w分别表示子体块在，，方向上的一阶位移梯度。

一阶形函数=[,,,u,u,u,v,v,v,w,w,w]共有12个参数，将整体素位移作为迭代的初始值，采用抗噪性能强的零均值归一化互相关函数（ZNCC）作为相关系数对离散数据进行处理，当变形前后的图像子体块灰度分布最为相似时，相关系数达到极值。

零均值归一化互相关函数（ZNCC）如下：

相关系数极值点应满足下列关系：

采用正向迭代的表达式为：

式中：p为第次迭代值；∇(p)为相关函数的一阶导数 向 量，即Jacobian矩阵；∇∇(p)为二阶导数，即Hessian矩阵。控制迭代的收敛条件，当满足 |p-p|≤0.001或达到规定迭代次数时，迭代终止。由于迭代过程中需要亚体素位置的灰度及灰度梯度信息，通常采用高精度的三元三次插值法对子体块的灰度进行插值处理以获得所需信息。

1.3 三维反向高斯-牛顿（IC-GN）算法

IC-GN算法的原理与FA-NR算法类似，但是迭代方向相反，IC-GN每次迭代过程中以目标子体块为不变量，参考子体块按照扭曲函数发生改变，其迭代参数以相乘的形式进行更新，如图2所示。IC-GN算法常采用零均值归一化最小平方距离相关函数（ZNSSD）用于评价子体块变形前后相似程度的衡量标准。

图2 IC-GN算法

零均值归一化最小平方距离相关函数（ZNSSD）为：

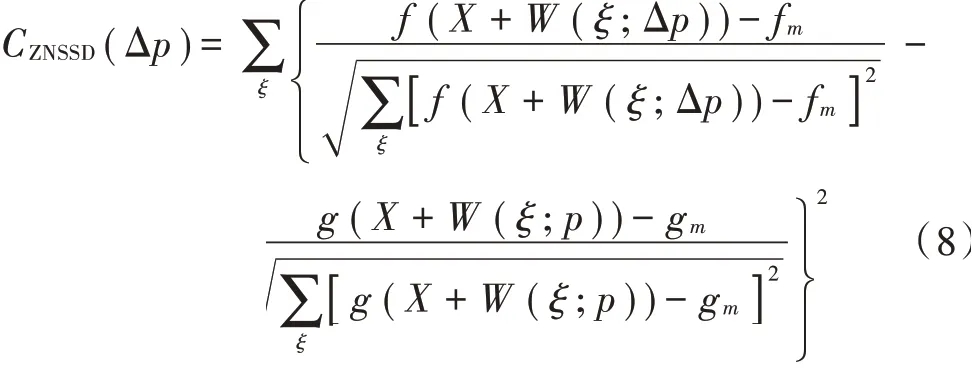
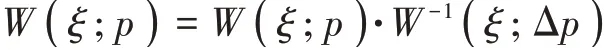
与正向算法类似，IC-GN算法达到收敛条件时停止迭代。除此之外，IC-GN算法同样也需要进行三元三次插值处理获得灰度梯度。

2 数值模拟平移实验

在实际应用数字体图像相关法测量位移时会受到三维层析图像采集系统、加载条件、室外环境等众多因素的影响，因而采用数值模拟实验的效果会比较理想。文献[12]将二维计算机模拟散斑图制作的方法扩展至三维可有效地模拟出三维散斑体图包含的灰度信息，该方法分为以下三步：

1）在一定范围区域内随机分布给定数量的点作为散斑的中心。

2）利用下式计算出该区域任意一点灰度：

式中：为散斑颗粒的总数；是散斑颗粒中心的光强强度且随机分布；为散斑颗粒的大小；(x,y,z)表示散斑颗粒中心的位置。

3）将以上所有信息保存为数字图像，便可以得到相应的散斑体图像。

通过设置以上参数可获得散斑数量为12 000个、半径为3 voxel、尺寸为150 voxel×150 voxel×150 voxel的三维散斑体图像，将该图像连续平移10次，每次移动0.1 voxel，直到最大位移为1 voxel时停止，得到10组刚性平移的体图像，并分别给平移前后的图像添加均值为0、方差为2的高斯噪声，如图3所示。将平移后的图像作为变形体图像，利用三种不同的亚体素算法计算图像的变形。

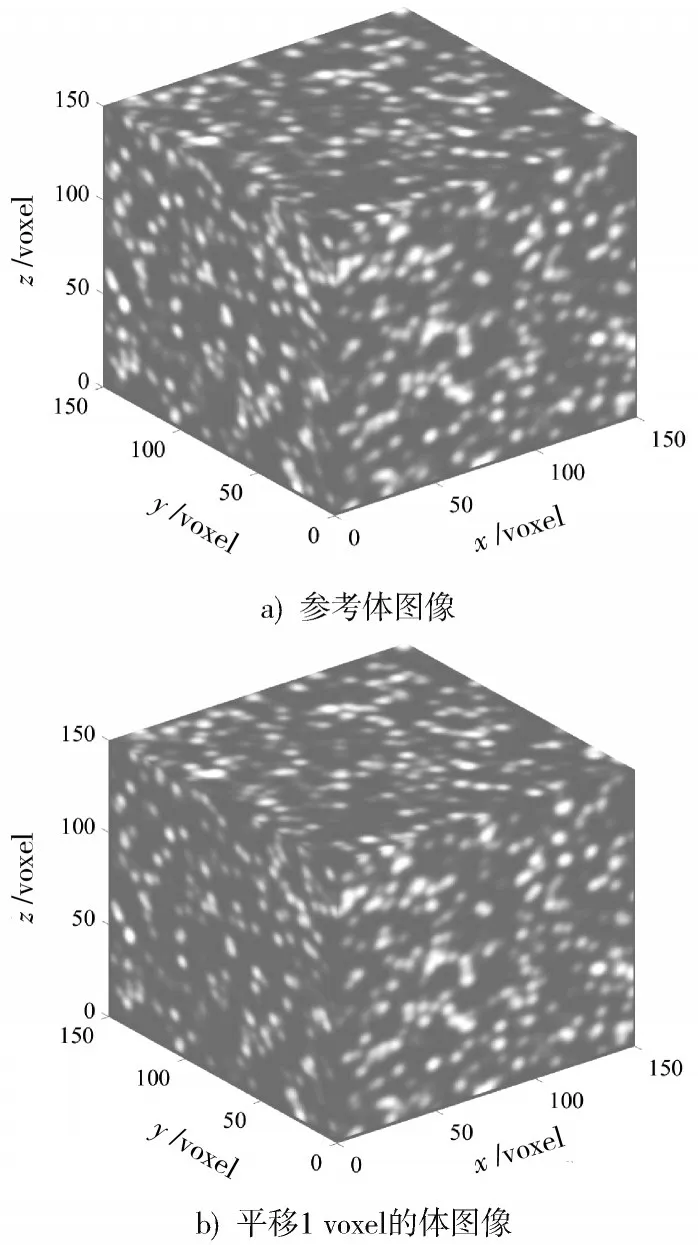
图3 计算机制作的散斑体图像

2.1 三种亚体素算法的精度比较

为了精准评价数字体图像相关方法在平移实验的测量误差，通常将计算结果与真实施加的位移对比。

均值误差（系统误差）为：

标准差（随机误差）为：

式中：u为数字体图像相关方法计算出第点的位移；为预加载的真实位移值；为计算点的个数。

使用三种方法对变形前后的体图像进行运算时，计算子体块的尺寸设置为21 voxel×21 voxel×21 voxel和41 voxel×41 voxel×41 voxel，计算步长均为10 voxel。不同算法对应的测量误差如图4所示，三种算法的均值误差都呈现出周期为1 voxel、近似于正弦曲线的分布规律，这与文献[13]中的误差规律基本一致。位移位于0、0.5 voxel和1 voxel时，测得的位移平均值最接近于真实值，均值误差接近于0；当施加的位移为0.2 voxel和0.8 voxel时，FA-NR算法和IC-GN算法测量位移的均值与真实位移相差最大，即均值误差为最大，而拟合算法在平移0.3 voxel，0.7 voxel对应的均值误差为最大。其次对比两个不同的计算子体块，位移的均值误差变化甚小，而标准差却成倍的减少，即计算子体块大小的选择对数字体图像相关法测量位移的均值误差影响不大，对标准差的影响却十分显著。

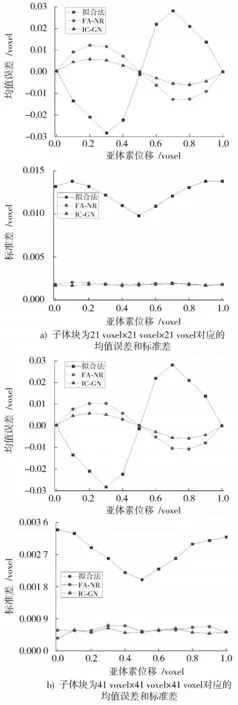
图4 不同计算子体块对应的测量误差

比较三种算法的测量误差，均值误差方面，IC-GN算法在不同尺寸的计算子体块中测量误差最大为0.006 0 voxel，约为拟合算法的1 5，FA-NR算法测量的最大值约为其2倍，而拟合算法的测量误差最大达到0.028 2 voxel，这说明IC-GN算法的测量精度要优于其他两种算法。标准差方面，IC-GN算法和FA-NR算法相近，且均小于拟合算法。在子体块为21 voxel×21 voxel×21 voxel时，IC-GN算法和FA-NR算法测得标准差均小于0.002 voxel，而拟合算法最大为0.013 8 voxel，由此可见拟合算法的稳定性明显更低。当子体块增大1倍时，三种算法的标准差减小了约4倍。

2.2 三种亚体素算法的计算效率比较

在数字体图像相关方法中，除了要考虑计算的精度外，计算效率也是值得考虑的因素之一，随着计算子体块的增大，计算效率均有不同程度的降低。三种算法均在计算子体块为21 voxel×21 voxel×21 voxel时计算效率最高，在子体块为41 voxel×41 voxel×41 voxel时计算速度最低。其次拟合算法的计算效率最高，IC-GN算法次之，FA-NR算法效率最低，如图5所示，以FA-NR的计算效率为标准。

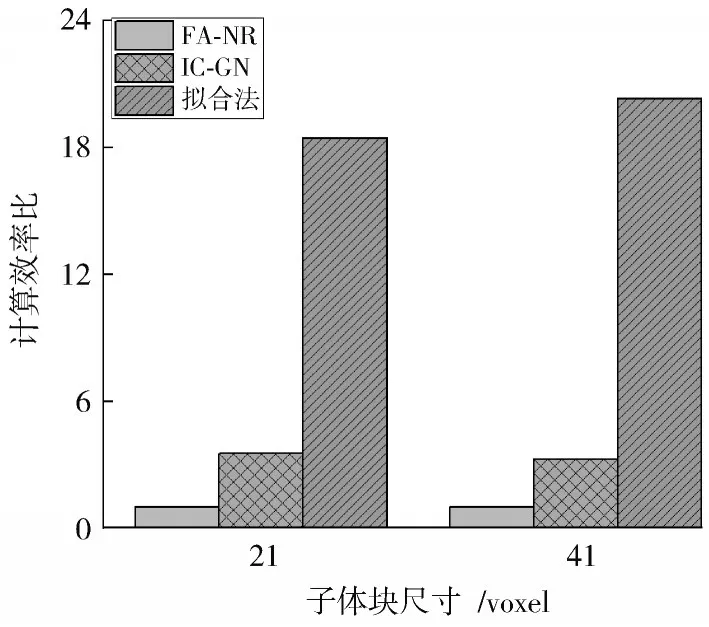
图5 计算效率比

在子体块为41 voxel×41 voxel×41 voxel时，拟合算法的计算效率是IC-GN的6.41倍，是FA-NR算法的20.34倍。探究其原因可能在于：拟合算法在计算过程中，不需要进行Hessian矩阵和子体块灰度插值的计算，且每次多项式只需计算一次即可，无需迭代，因此拟合算法具有较高的计算效率。FA-NR算法在每次迭代过程中会反复计算Hessian矩阵，且亚体素位置的灰度和灰度梯度信息需要反复利用三元三次插值获得，这将极大消耗计算时间和内存。而在IC-GN算法的迭代过程中，由于采用反向迭代的策略，Hessian矩阵只需要计算一次即可，迭代次数显著减少，提高了计算效率。综上分析，IC-GN既保证了计算精度的同时也提高了计算效率，FA-NR算法则是以牺牲时间而获得较高的测量精度，而拟合算法的计算效率最高但是计算精度最低。

3 零应变原位扫描实验

零应变原位扫描的实验对象为正常成年男性腰椎标本，由昆明医科大学捐赠，如图6所示。测试时，将实验样品放置在Micro CT-225上进行零应变原位扫描，扫描期间样品没有任何移动，扫描时长约为15 min，并将扫描图像以39μm的各向同性体素尺寸重建。CT设备扫描试件时并没有发生移动，理论上物体没有发生变形，然而由于多种因素的影响，如CT射线热误差、算法误差、体图像质量等，必然导致测量结果有少许偏差，且这些误差并不能完全消除。由于运算时采用相同的体图像，测量结果可直接用于对比三种算法的测量误差大小。

图6 椎骨体图像及其灰度分布图

利用数字体图像相关方法测量椎骨变形时，计算子体块大小选择为21 voxel×21 voxel×21 voxel，计算步长设置为5 voxel。三种算法的测量误差如图7所示，其中拟合算法的误差最大，FA-NR算法和IC-GN算法的误差相对较小且基本相同。

图7 三种算法的测量均值绝对误差和标准差

虽然算法不同，但是误差最值出现的方向一致，即均值绝对误差最大值在轴，标准差则出现在轴方向。在计算精度方面，IC-GN算法精度最高，其均值绝对误差在0.057 5～0.146 9 voxel范围内，FA-NR算法的误差为0.058 9～0.148 5 voxel，而拟合算法精度最低，其误差范围为0.063 1～0.159 7 voxel。在计算稳定性方面，IC-GN算法的表现最优，其标准差为0.057 5～0.146 9 voxel，FA-NR算法的标准差为0.059 6～0.014 85 voxel，拟合算法稳定性最差，其标准差范围为0.062 1～0.155 2 voxel。需要特别注意的是，三种算法在零应变实验中的误差最值要明显大于平移实验中的最值，由此可见零应变实验的误差主要是由外部因素引起，而算法误差所占比例相对较小。综合分析，FA-NR算法和IC-GN算法在椎骨原位扫描下测量的精度及稳定性也均优于拟合算法。

4 结 论

本文简要地介绍了三种常见的亚体素位移测量算法：拟合算法、FA-NR算法和IC-GN算法，通过两组不同的实验对比三种算法的计算精度及其稳定性，结果显示IC-GN算法的性能最优。在散斑体图像的平移实验中，三种算法的计算精度均随着子体块的增大而提高，但是计算效率却成倍的递减。其中IC-GN算法的测量精度最高，而拟合算法的测量误差和稳定性均为最差，而其计算效率最高。在椎骨零应变测试中三种算法表现的性能也不尽相同，IC-GN算法和FA-NR算法的测量精度均优于拟合算法。其次对比两组实验可发现平移实验的测量精度要高于零应变测试的精度，主要原因是外部因素引起的误差要大于算法误差。综合对比计算精度和计算效率，可确定IC-GN算法为数字体图像相关方法中的最佳亚体素位移测量算法。

注：本文通讯作者为许蔚。