结合梯度差分和Otsu自适应边缘检测算法

王 静，唐文豪

（西安科技大学 通信与信息工程学院，陕西 西安 710054）

0 引 言

边缘检测是图像处理与分析中的一项基本的计算机视觉处理技术，许多学者提出了许多相关算法，如Robert、Prewitt、Kirsch、Gauss-Laplace、Canny等。其中，Canny算子具有很好的信噪比和检测精度，在图像处理领域得到了广泛的应用。

传统Canny算子对噪声比较敏感，高斯滤波使边缘模糊，易丢失边缘信息，为此许多学者提出了改进的Canny算子，如梯度倒数加权滤波方法对图像进行斑点噪声滤除的同时保持了图像边缘；利用形态学的开闭操作滤波抑制毛刺噪声和桥噪声，并且可以平滑图像边缘的边界点；通过图像一阶直方图的统计特性自适应地选取高斯滤波器的参数，有效去除了噪声。针对传统的Canny算子阈值选取不具有自适应的特点，文献[4]利用图像的梯度方差作为判据对图像进行分块，继而对各子块运用最大类间方差法求得相应的阈值；文献[5]直接使用Otsu方法自适应计算阈值；文献[6]通过构造梯度方向和SGD指标自适应确定阈值。本文用非线性滤波器双边滤波代替高斯滤波，通过调节双边滤波的参数达到保边去噪的目的，接着提出一种差分梯度直方图结合Otsu的方法，相比文献[5]直接使用Otsu的方法，在自适应确定阈值的同时，大大减少了迭代次数，加快算法运行时间。最后通过一种递归边界跟踪边缘连接方法将断边连接起来。

1 传统Canny算法

Canny提出了一种很有效的边缘检测算法，该算法的实现主要有如下四个步骤：

1）使用高斯滤波器对原图像进行滤波。

2）采用水平和垂直两个方向的一阶偏导数计算图像的梯度幅值(,)和梯度方向(,)：

3）对梯度图像进行非最大值抑制操作，以细化边缘。

4）用高低双阈值连接最后的边缘，高、低阈值大小的选择对最后边缘连接有着至关重要的影响。若某一像素的梯度值大于高阈值，直接当作强边缘点；若某一像素的梯度值小于低阈值，直接置0；若某一像素的梯度值介于高、低阈值之间，则通过寻找该像素点八邻域内有没有强边缘点，有，则保留该像素，否则，被排除。

2 改进的Canny算子

2.1 双边滤波

当图像中存在明显的边缘信息时，通常的邻域运算必然会导致图像中边缘点的像素值发生变化，使图像的边缘变得模糊不清。而Canny算法中的高斯滤波只考虑了像素间空间位置上的关系，易造成边缘模糊，以此造成边缘信息的丢失，因此高斯滤波方法很难做到兼顾平滑噪声和保护边缘信息。为了改善这一现象，本文提出双边滤波的方法，双边滤波器模板的卷积权值的选取不仅取决于普通低通滤波的像素空间位置关系，同时考虑了像素间的相似程度，双边滤波可表示为：

式中：I(,)为输出像素值；(,)为窗口内各个像素点的值；ω为空间域高斯函数；ω为像素间亮度高斯函数。

以Lena图像为例进行高斯和双边滤波实验，如图1所示。

图1 高斯滤波与双边滤波对比结果

由图1c）和图1d）可以看出，高斯滤波图像模糊，双边滤波比高斯滤波去噪效果更显著，并且能保留更加完整的图像边缘信息。

2.2 梯度计算

传统的Canny算子使用水平和垂直两个方向Sobel算子计算梯度，即计算水平和垂直邻域内的差值，对于梯度变化相对缓慢的边缘，只考虑两个方向的模板计算易丢失梯度信息。因此本文增加45°和135°方向Sobel梯度模板计算，一方面解决只考虑两个方向模板计算的局限性，另一方面，在一定程度上突出梯度差相对弱的边缘。Sobel梯度模板如图2所示。

图2 Sobel梯度模板

则梯度幅值可表示为：

式中：G,G,,分别为四个方向模板卷积结果。

梯度方向为：

2.3 自适应阈值选取

2.3.1 Otsu算法

一幅大小×像素的数字图像有个不同的灰度级，n为灰度级为的像素数，归一化的直方图分量P=n()，选择一个阈值()=，0＜＜-1，将图像分为两类和。由图像中灰度值在范围[0,]内的像素组成，由灰度值在范围[+1,-1]内的像素组成。

像素分配到类中的概率()为：

类中像素的平均灰度值为：

同理，类中像素的平均灰度值为：

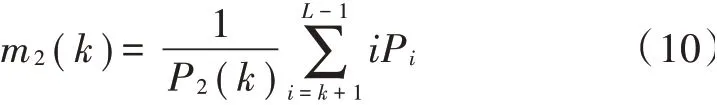
整幅图像的平均灰度值为：

类间方差定义为：

式中，初始阈值的范围为[0，]，使最大的值作为Otsu的最佳阈值。

2.3.2 梯度直方图的分析

Lena图像经过非极大值抑制后，得到一幅梯度直方图，横坐标为梯度幅值，纵坐标为各梯度幅值对应像素点的频率，如图3所示。图4为局部放大图。

图3 梯度幅度直方图

图4 局部放大图

经多次实验，梯度直方图具有以下特点：

1）图像的背景区域梯度幅值较小，占了大部分比例，梯度直方图的曲线在背景区域急剧下降，随后边缘缓慢。

2）在急剧下降过渡到平滑区域的区间内存在零点，零点右侧的尖峰代表一类边缘强度像素点的集合，阈值选在平滑区域与尖峰之间才能更好地较少误差。

通过对梯度直方图的分析，阈值选取在平滑区域误差最小，因此Otsu算法的迭代阈值应包含此区间，而直接应用Otsu需要遍历所有的梯度值，通过一阶差分梯度直方图得到第一个过零点的值，作为Otsu算法初始阈值，通过计算二阶梯度直方图，定义参数，使得二阶差分小于时对应的梯度值作为上限值，参数通过实验得到。

定义梯度直方图为()，一阶差分为diff，二阶差分为diff′，则：

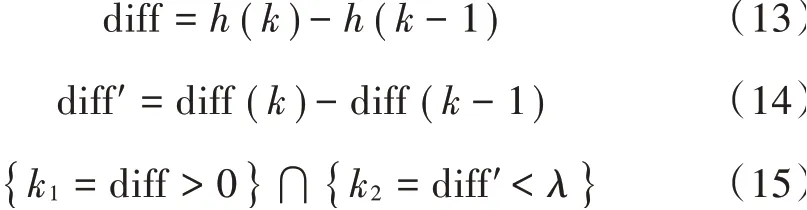
梯度直方图一阶差分diff、二阶差分diff′计算结果如图5所示。式（15）为，的约束条件，那么在[，]中应用Otsu法得到的阈值作为Canny边缘检测的高阈值误差最小，且减少了Otsu算法的迭代次数，加快了算法的运行时间。与文献[5]算法运行时间比对，结果如表1所示。

图5 差分图

表1 算法运行时间比对

2.4 边界跟踪边缘连接方法

传统的Canny算法采用双阈值连接，大于高阈值的值直接置为强边缘，介于高、低阈值之间的值通过寻找其八邻域内有没有强边缘决定该值是否为边缘点，这种方式对于断裂的边缘没有任何改进，图像经过非极大值抑制后，如图6所示，大于highthreshold的边缘图像在轮廓上有断裂。大于lowthreshold的边缘图像含有强边缘、弱边缘、伪边缘，如图7所示。

图6 高阈值图像

图7 低阈值图像

顺时针遍历搜寻高阈值图像中所有端点，将端点作为初始引导点，找到差异图中对应的点，如果差异图（见图8）的点满足一定关系，则将边缘存下，通过递归跟踪算法在差异图中搜集边缘，断裂的边缘会得到很好的连接，且伪边缘和噪声点不会被连接。

图8 差异图

常用端点判别方式：经非极大值抑制后的边缘可以分为端点、边缘点和孤立点，即在八邻域中有1个点相连为端点；有2个及以上的点相连为边缘点；没有点相连为孤立点，如图9所示。

图9 边缘点类别判断图

本文边缘连接的思想为以高阈值图像作为引导，计算高阈值图像和低阈值图像之间的差异图。寻找高阈值图像中的端点，在差异图中对应的点搜索其八邻域中有没有点与边缘线相连，有，则将该点连接到高阈值图像中，并将该点更新到端点集合中，直到将高阈值图像中的断边连接起来。

本文边缘连接的步骤如下：

Step1：非极大值抑制后得到高阈值边缘图像；

Step2：得到低阈值边缘图像；

Step3：遍历高阈值边缘图像，根据判别方式得到端点；

Step4：计算高、低阈值图像的差异图；

Step5：根据端点寻找邻域内满足条件的点，将该点连接到高阈值图像，并将端点集合更新；

Step6：重复Step5，直至将断裂边缘连接。

整个算法流程图如图10所示。

图10 算法流程图

3 实验结果及分析

本文在Matlab 2014b上实验，实验图像分别为Lena、Peppers和人像图，如图11所示。由图中结果可以看出，相比传统Canny算子，Lena图像在脸庞处和顶端连接上了断边，Peppers在中部断边处也得到了很好的连接，人像图在袖子处的边缘更加完整且连续。

图11 传统Canny与改进Canny实验结果

为验证边缘检测结果的性能，采用信噪比指标和文献[7]给出的指标对传统Canny和改进Canny边缘检测结果进行统计。信噪比（SNR）定义为：

式中：为边缘检测结果所有点3×3邻域存在像素点个数大于3的总数；代表边缘检测结果3×3邻域像素点不大于3的总和。

指标计算结果如表2所示。结果表明，改进算法SNR指标高于传统算法，说明改进Canny算法边缘信息更丰富，边缘连接性更好。

表2 SNR统计

第二种指标统计结果如表3所示。其中：代表检测出的边缘像素总数，代表4连通数，代表8连通数，评价方法为计算和的值，的值越小，说明检测结果的单边缘响应越好，的值越小，说明算法检测结果的连续性强，边缘间断少。结果表明，改进算法单边缘响应效果好，边缘检测的完整性和连续性也优于传统算法。

表3 边缘结果图像统计

4 结 语

本文对传统Canny算子进行了改进，采用双边滤波代替高斯滤波滤除噪声的同时能够保持边缘信息，梯度计算增加45°和135°两方向的模板以突出边缘信息，接着对Canny算法进行自适应阈值计算，最后提出递归边界跟踪的边缘连接方法。实验结果表明，改进的算法边缘连接性和完整性都优于传统Canny算法。