sEMG多特征融合的自适应神经网络下肢运动意图识别研究

刘瑞恒，张峻霞，钱芊橙

（1.天津科技大学 机械工程学院，天津 300222；2.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津 300222）

0 引 言

可穿戴设备广泛应用于康复医疗、军事助力、休闲娱乐等领域。据调查，国内与康复医疗相关的可穿戴设备多达150种，其中下肢外骨骼机器人成为许多学者研究的热点，该设备在军事上作为军人的助力装备，在医疗领域作为下肢运动障碍患者的康复辅具。对于外骨骼机器人而言，下肢运动意图识别是其实现主动训练的前提，识别动作的数量直接影响其整体功能。

根据肌电信号的特性可知，肌电信号的产生总是早于人体的实际动作，人体运动之前的500 ms肌肉就会产生电信号。有研究表明，肌电信号源算法的稳定性优于机械信号源算法，如果在肌电信号产生300 ms之内能够识别下肢动作就可以做到运动意图的识别，而且表面肌电信号（Surface Electronomyography，sEMG）具有易采集、对人体无损伤的优点。因此，表面肌电信号作为信号源识别人体步态是一个重要的研究方向。

基于机器学习的sEMG识别是一种重要的方法，下肢动作识别最常用的机器学习方法有：支持向量机（SVM）、人工神经网络（ANN）、深度卷积神经网络（CNN）、K近邻算法（KNN）等。sEMG信号的特征一般有以下几种：时域特征（如平均绝对值和过零点数等）、频域特征（如平均功率频率和短时傅里叶变换等）、时频域特征（如小波变换）和样本熵。文献[17]分别提取时域、时频域和熵特征三种特征对脑瘫儿童的不同肌肉活性对比研究，结果表明时域和熵特征有更好的效果。文献[18]提出基于小波包能量分析的肌肉疲劳识别方法，该方法可以快速地检测肌肉收缩和松弛状态。文献[19]使用排列组合熵特征对手部四种动作信号进行识别，该特征很好地反映了肌电信号的细微变化。目前，下肢动作识别的研究已经取得了较好的成果，但是下肢运动意图识别存在许多难点问题，如：单一特征训练的识别模型识别准确率低，传统识别模型识别时间较长，不能达到意图识别。

针对以上难点问题，本文通过采集下肢8块肌肉（左右腿的腓肠肌、股直肌、半腱肌和股外侧肌）的表面肌电信号，使用小波基函数对原始信号进行降噪处理，采用信号能量阈值法自动分割sEMG信号，提取时域、小波和样本熵特征，通过主成分分析法剔除冗余特征，并利用差分进化算法优化特征的权重值，实现多特征向量优化组合。使用动态自适应学习率的神经网络算法，既提升了模型的收敛速度，又提高了模型的识别精度，最终实现下肢8种运动意图识别，并验证了该方法的有效性。

1 人体下肢运动的识别实验

1.1 实验对象

实验对象包括50名受试者，身高在165～185 cm之间，体重在60～80 kg之间。在实验开始前告知受试者8种实验动作以及动作要求，所有受试者采集前熟悉实验动作及实验过程，进行3～5 min的热身和拉伸运动。受试者实验前半年均无下肢肌肉、膝关节和踝关节手术，且均表示自愿参加本次实验。

1.2 实验过程

实验中，采集肌电信号的设备是美国Noraxon公司研发的Telemyo 2400DTS表面肌电遥测器，该产品可以实现16通道表面肌电信号的无线实时传输，采集频率为1 500 Hz。在采集实验进行之前，对受试者腿部用酒精擦拭除去角质，选取其中8个通道分别采集左右腿8块肌肉的表面肌电信号，通道1～8分别对应受试者的左腿腓肠肌、右腿腓肠肌、左股直肌、右股直肌、左半腱肌、右半腱肌、左股外侧肌和右股外侧肌。把专用电极片贴于肌腹位置，且肌电片的方向与肌肉纤维的方向相同，如图1所示。

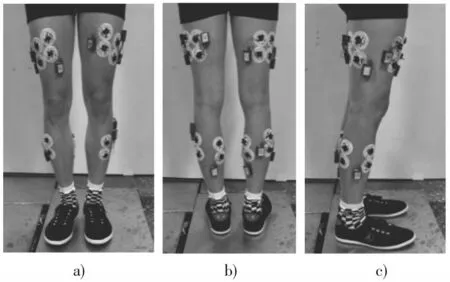
图1 受试者肌电片所贴肌肉位

50名受试者分别完成平地行走、上楼梯、下楼梯、左转、右转、起立、坐下和慢跑8种动作，每个动作10次为一组，每种动作做5组。每种动作完成后休息5 min。

2 实验数据分析方法

本文利用Matlab进行数据处理，实现对下肢动作的意图识别。下肢动作识别的流程图如图2所示。

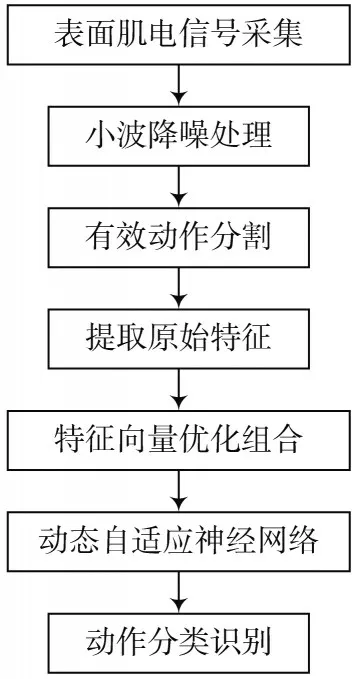
图2 下肢动作识别的流程图

2.1 数据预处理

表面肌电信号属于典型的非平稳性随机信号，具有很高的敏感性，容易受到外界噪声、电极和电力线的干扰，这些污染源会影响模型的分类结果。本文利用小波变换对sEMG信号去噪，小波变换技术可以有效地对时间和频率分量进行分解，把信号分解到不同的频域并对信号进行滤波。本文采用离散小波变换（DWT），选取“sym6”小波母函数对信号进行降噪处理，最终取得了良好的效果，如图3所示。

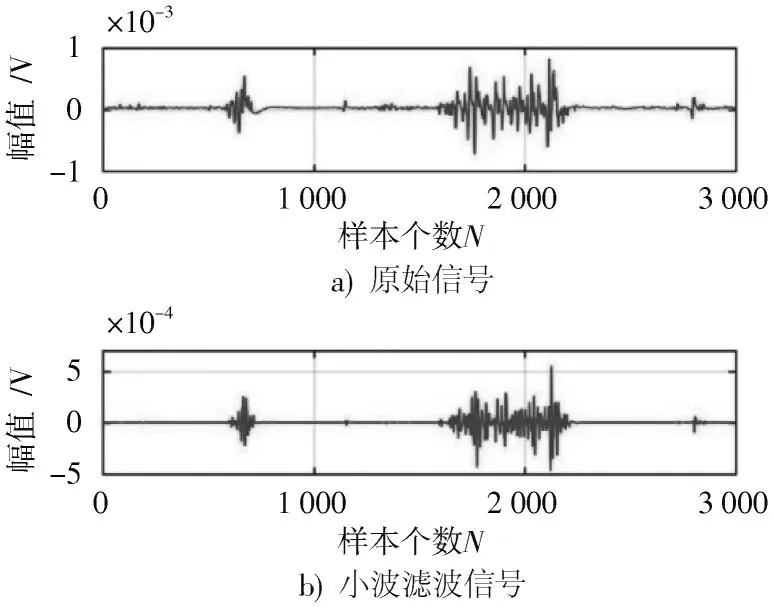
图3 原始信号和小波滤波信号的对比图

2.2 有效动作段划分

受试者采集每个动作完成后，需要将肌电信号进行有效精确的划分，除去无动作信号，寻找动作的始末点，提高模型的分类准确率并且降低肌电信号的数据处理量，加快程序的运行和分析速度。

肌肉的收缩程度与肌电信号的强度具有相关性，因此，采用信号能量阈值法自动分割sEMG信号，以肌电信号窗口的能量值作为动作的判断依据。选取400个数据样本点长度的滑动窗对肌电信号进行扫描，把滑窗内数据的波形长度（Wave Length，WL）作为特征向量，该特征值的大小作为肌肉有无运动的判决标准。波形长度是信号幅值、频率及持续时间的综合效果，反映信号复杂程度，定义如下：

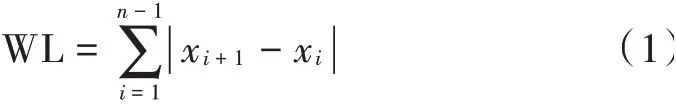
设置阈值，当波形长度大于阈值，窗口（）有动作且标记为1，否则为0，（）定义为：

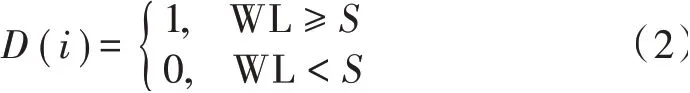
假设当前窗口为（），窗口向后依次滑动计算波形长度并计算（），当（）的值由0变为1时，判定该点为动作起始点，反之，该点为动作结束点。动作划分计算过程如图4所示，其中图4a）是某一受试者在平地行走动作的右股直肌电信号的一部分，图4b）和图4c）中，第一个和第二个波峰分别对应一个步态周期的支撑相和摆动相，且支撑相比摆动相的峰值大，动作的起始点和结束点判断准确。

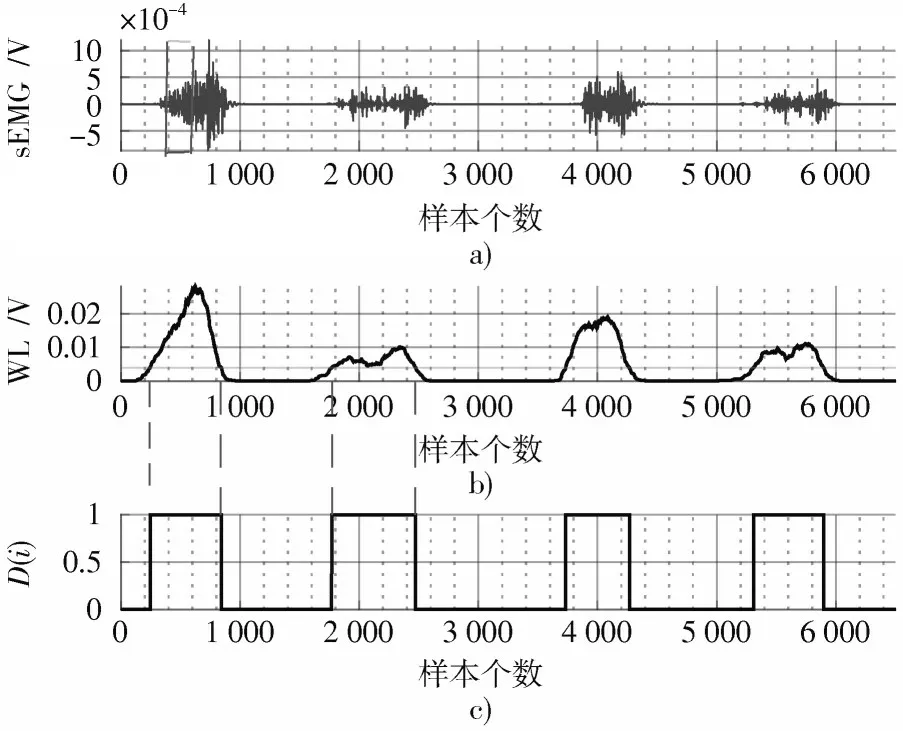
图4 动作划分计算过程

最后，通过该方法实现8种不同动作的肌电信号起始点的自动分割，当受试者存在步态差异、身体差异等因素时，也能保证分割结果准确。

2.3 提取原始特征

由于表面肌电信号的复杂性，所以正确选择信号特征是分类的关键一步。对于不同的下肢运动动作，很难通过提取出一个特征参数完全反映被测表面肌电信号的特征，因此对肌电信号进行分类时需要使用多个特征参数。时域特征主要有绝对平均值（Mean Absolute Value，MAV）、斜坡变更数（Slop Sign Change，SSC）、过零点数（Zero Crossing，ZC）、波长（Waveform Length，WL）、均方根（Root Mean Square，RMS）。传统的频域特征是基于平稳信号假设为前提，而表面肌电信号属于非平稳时变信号，传统的频域特征会丢失信号时间的信息。小波变换具有时域和频域两方面的信息，表现出的信息更加全面和丰富。

小波变换能够表达不同频域段的特征，通过伸缩平移运算对信号逐步进行多尺度细化，达到高频和低频处频率细分，能适应肌电信号分析的特点，其表达式如下：

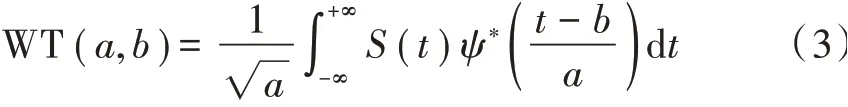
式中：（）代表分析信号函数；“*”代表复共轭；代表小波函数；WT（，）是小波变换后的系数，为伸缩因子，为平移因子。用不同小波函数的线性组合对原信号进行重组，如下：

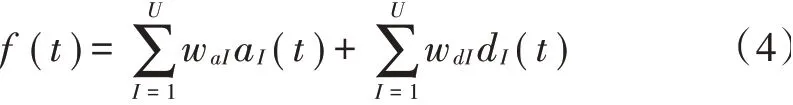
式中：w为低频小波系数；a（）为低频小波函数；w为高频小波系数；d （）为高频小波函数。小波分解层数为，则有2个子空间，把分解后的子函数记作W。Symlets（sym）小波函数系是一种近似对称的小波函数，该函数具有很好的非线性相位。本文使用Matlab工具箱，选取sym4小波函数系对肌电信号进行5层小波分解，共有2=32个子空间特征。

样本熵（Sample Entropy，SE）是一种分析非线性时间序列信号的方法，能够充分反映时间序列信号的复杂性，该方法适合分析非平稳、非线性的肌电信号。该特征的计算方式如下：

公式（5）中，（）为表面肌电信号，[（），（）]表示（）与（）之间的距离为两者对应元素中差值的最大值：

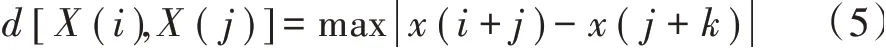
公式（6）给定相似容差，统计[(),()]＜的模板匹配数，并对距离总数--1求均值，得到所有-条件下的模板匹配数的平均值，记为B（）：

联合式（5）、式（6）得到数据长度为的表面肌电信号的样本熵值为：

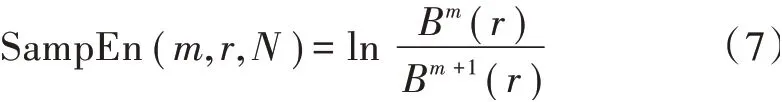
3 基于多特征融合的自适应BP神经网络

3.1 主成分分析法特征降维

Step1：将样本数据标准化，得到标准化矩阵。

Step2：计算样本的特征相关矩阵=(r)，如下：

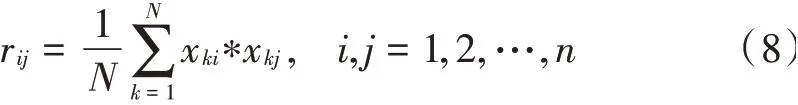
Step3：求 |-|=0的特征值以及特征向量，其中为单位矩阵，为协方差矩阵的特征值。

Step4：求各个成分的贡献率，并选取前个满足贡献率大于90%的主成分。

Step5：求解个主成分的特征向量，作为新的输入特征。

采取如上步骤对时域特征、小波分解子空间和样本熵使用主成分分析法降维，降维后的sEMG特征之间互不相关，能够最大程度地包含原特征的信息。

3.2 基于CNN的差分进化算法特征融合

为了更好地设置时域、小波变换特征和样本熵的权重，引进了差分进化算法寻找最优权值。差分进化（Differential Evolution，DE）算法是一种高效的全局优化算法，具有结构简单、收敛快速、鲁棒性强等优点，因此被广泛应用于数据挖掘、模式识别、神经网络等各个领域。针对表面肌电信号多特征融合的问题，本文提出一种改进的差分进化算法。

习近平总书记对浙江工作重要指示、全国组织工作会议和省委十四届三次全会精神，对新时代组织工作作出了一系列新部署，提出了一系列新要求。我们一定要以勇于自我革命的决心和勇气，不断推动组织工作创新发展。要以“八个有机融合”的方法和手段，“五个品格”“五个带头”的要求和目标，不断推动组织部门自身建设，充分展示新气象新作为。要以“大学习大调研大抓落实”的措施和行动，不断推进能力大提升、作风大转变，为“‘八八战略’再深化、改革开发再出发”提供坚强组织保障。

按照公式（9）将时域特征f、样本熵特征f和小波特征f融合，得到融合特征f。

在融合三种特征时，为了提高实验的准确率，本研究对三种特征进行标准化处理。权值，和的适应度评价函数由次交叉验证分类结果的平均分类结果和下肢动作分类结果错误的数量决定。

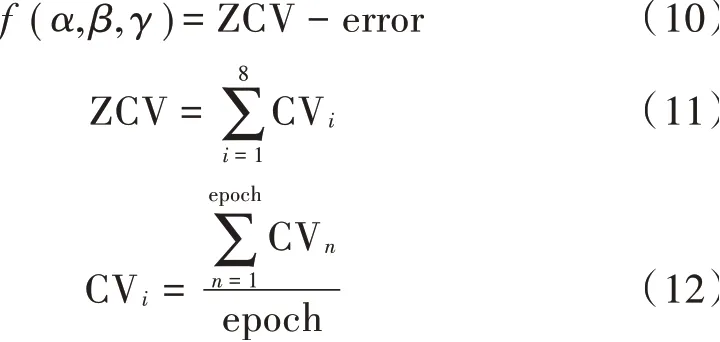
式中：是epoch的个数；CV 是一次交叉验证的平均分类结果；ZCV是8次交叉验证的平均分类结果；error是下肢动作分类结果错误的数量。

针对下肢表面肌电信号不同特征融合优化的问题，对DE算法进行改进，通过增加参数自适应方法提高算法的收敛速度，更快速地找到最优解。DE算法的主要参数有交叉率和放缩因子，这两个参数的好坏很大程度决定了算法性能，本文采用文献[24]快速自适应方法。与CR的自适应控制见式（13）和式（14）：

式中：为放缩因子；CR为交叉率；为所有个体适应度的平均值；为适应度值的最大值。将arcsin()作为依据，当该值小于π6时，说明种群的适应度值比较分散，应该自适应地增大交叉率CR的值，并且自适应地减小放缩因子的值；反之，亦然。由于加入自适应参数的方法使子代获得更好的分布性，加快算法收敛速度，避免陷入局部极值，更好地找到全局最优解。根据标准的差分进化算法，得到基于改进差分进化算法优化的融合特征权值的DE算法，具体步骤如图5所示。

图5 改进的DE算法流程图

3.3 动态自适应神经网络运动意图识别

BP神经网络（Back Propagation Neural Network，BPNN）是一种由输入层、一个或多个隐含层以及输出层组成的前馈型神经网络，同一层级的神经元相互独立，相邻层级的神经元互相连接。该算法的原理是：通过训练样本的结果与实际结果比较，对两者误差使用反向传播算法修正神经网络的连接权值和阈值，经过反复计算使误差小于一定的值，该模型可以对未知的变量进行预测。

然而，标准BP神经网络存在学习率确定难、收敛速度慢的问题。对于此问题，本文提出通过附加动量改进修正权值和偏置过程的方法和学习率自适应调整方法，将上述两种方法结合起来，形成一种动态自适应神经网络模型（Dynamic Adaptive Neural Network，DANN），该模型是在BP神经网络的基础上加入自适应学习率改进而来的。该方法的核心是引入自适应学习因子，学习因子根据神经元梯度值动态更新学习因子，并且选择交叉熵函数作为损失函数，其公式为：

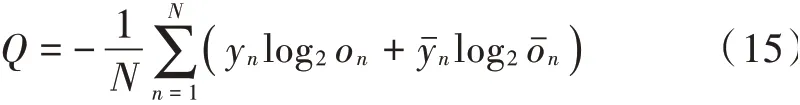
对于标准的BP神经网络输出层权值和隐含层权值的更新方法如下：

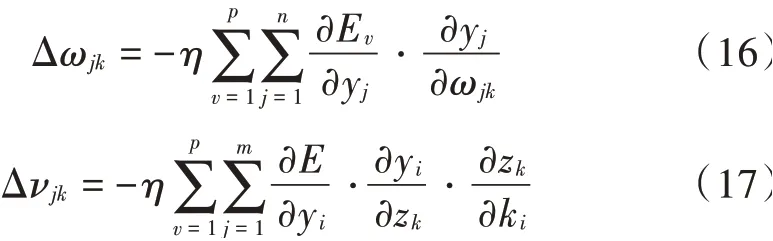
式中：ω是第次迭代的参数调整量；为学习率；E为第个样本误差；y为输出层节点的输出。

在添加附加动量项后，神经网络梯度下降的参数更新项为：

式中g（）为第次迭代计算出的梯度。

由于动量因子取值为0～1。式（18）也等价于：

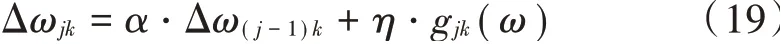
式中：称为遗忘因子；·Δ表示上一次梯度对当前梯度下降的调整影响值。

附加动量法存在学习率选取困难的问题，进而产生收敛速度与收敛性之间的矛盾，因此，引入动态自适应学习率方法：

将上述两种方法结合，形成改进的动态自适应学习率神经网络流程图，如图6所示。

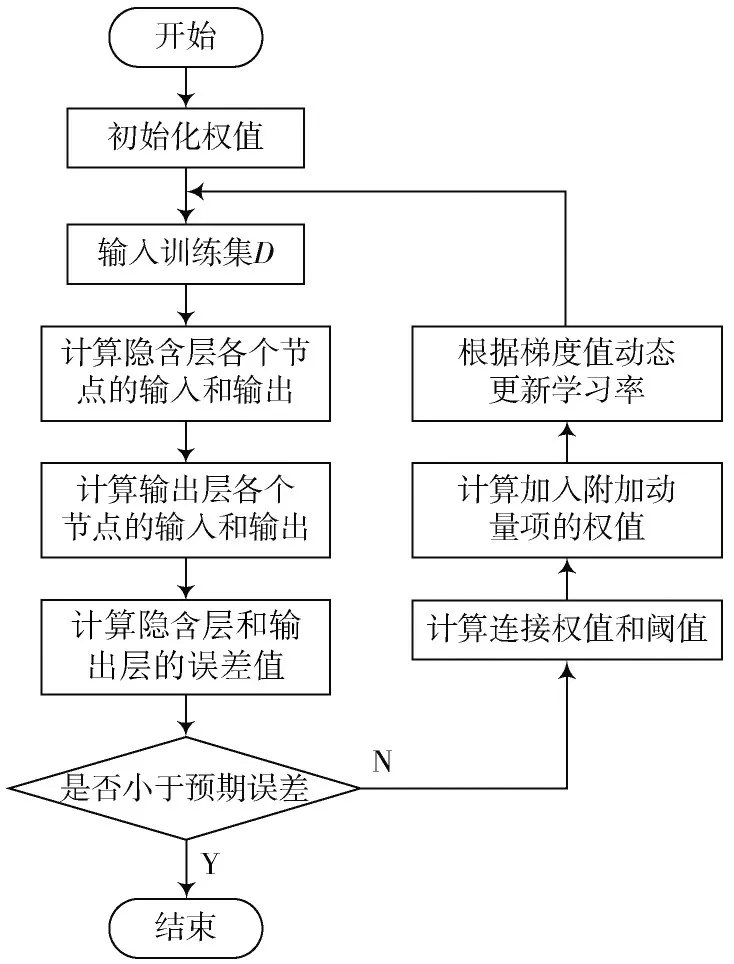
图6 改进的动态自适应学习率神经网络流程图

4 实验结果与分析

4.1 主成分与DE算法多特征融合分析

把上述实验中采集的sEMG信号进行特征提取，原始肌电信号的时域、小波特征和样本熵是一组高维数据，其中包括许多冗余信息。本文使用主成分分析法分析特征，选取贡献率前10的主成分作为特征向量。主成分分析贡献率和累积贡献率如表1所示。由表1可知，前10个主成分的累积贡献率达到92.43%，基本包含了全部的信息。

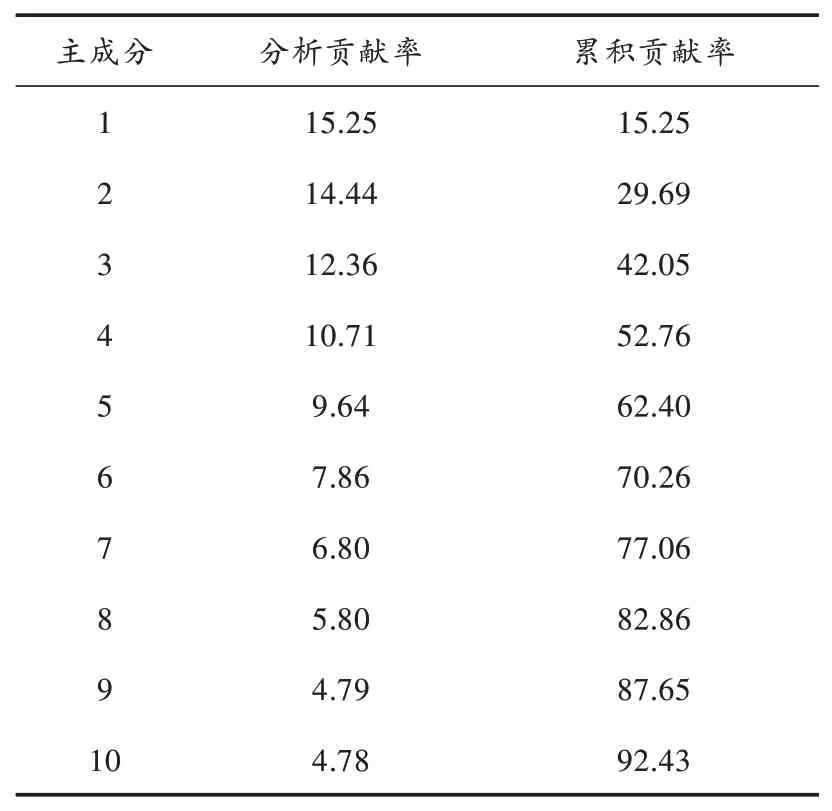
表1 主成分分析贡献率和累积贡献率 %

由表1可知，肌电信号的主要信息集中在贡献率排名前10的主要成分中，它们分别是：样本熵（SE）、绝对平均值（MAV）、过零点数（ZC）、波形长度（WL）、斜坡变更数（SSC）、均方根值（RMS）以及4个小波分解子空间。

随机选取1名受试者的数据，对8种下肢动作的sEMG信号进行识别，使用保持法（Holdout）把数据划分为两个不相交的集合，一部分作为训练集，剩余的部分作为验证集，在验证集上评价模型的性能，两个集合的划分比例为2∶1，每种动作60组数据，选取其中40组数据作为训练集，20组作为验证集。根据主成分分析法对特征贡献率的大小依次加入特征集识别，特征维数与动作分类准确率的关系如图7所示。

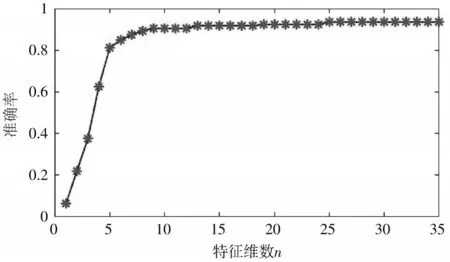
图7 特征维数与动作分类准确率曲线图

特征维数与动作分类能力的关系曲线表明，模型识别的准确率随着特征维数的增加而增加；但是，当按照主成分分析法排列的特征集维数增加到10时，动作意图识别的准确率基本趋于稳定；当特征维数超过10，识别模型的准确率只有很小的提高。随着特征维数的增加，识别模型的训练和识别时间会增加。因此，PCA法对特征降维取得很好的效果，不仅保留了主要信息，还提高了识别模型的性能。

对于不同的特征融合权值，和会影响模型的识别效果，本文采用差分进化算法求解融合特征的最优权值。设置改进差分进化算法的进化代数为80，种群规模为30，交叉因子为0.8，变异因子的初始值为0.6，在算法不断迭代过程中变异因子会不断更新。改进的DE算法经过53次迭代后模型的误差已经趋于稳定，此时得到融合特征的最优权值。

4.2 动态自适应神经网络识别算法性能分析

不同受试者的身体状况和生活习惯导致个体的步态存在差异，受试者的肌电信号也具有一定的差异性。为了增加模型的鲁棒性，将50名受试者的数据混合在一起组成新的数据集，对新数据采用折交叉验证（-fold Cross-validation）进行分割，分别使用传统BP神经网络和动态自适应神经网络对8种动作进行识别。当=6时，将混合数据样本分割成6组，其中的5个样本数据作为训练集，剩余的1个样本数据作为验证集。交叉验证重复6次，6次识别结果的平均准确率作为该模型的准确率。

将改进的动态自适应神经网络简称为DANN，多特征融合BP神经网络模型简称为MBPNN，基于多特征融合的动态自适应神经网络称为MDANN。BPNN、MBPNN和MDANN分别在测试集的性能曲线对比图如图8所示。

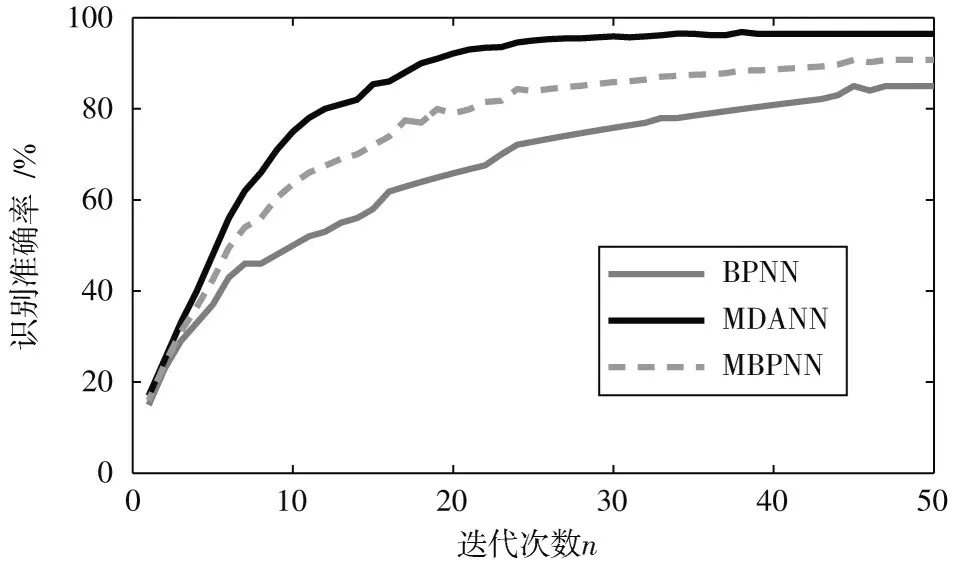
图8 不同识别算法在测试集上的性能曲线对比图

由图8可知：和BPNN相比，MBPNN经过融合权值的重新加权，使得时域、小波子空间和样本熵不同的特征充分表达自身所包含的信息，从而提高模型的识别精度；与MBPNN相比，MDANN加入动态自适应学习因子，提高了模型的收敛速度。

为了进一步对比传统BP神经网络与动态自适应神经网络的性能，图9比较了时域、小波子空间、样本熵和优化组合特征分别在传统BPNN和DANN模型中训练集和测试集识别准确率，无论是在测试集还是训练集，DANN模型都优于传统BP神经网络，并且多特征融合的自适应神经网络模型的识别准确率优于单一特征神经网络模型；在模型的识别时间方面，时域特征模型的识别时间最短，耗时206 ms，其他特征模型的识别时间基本相同，分别为294 ms、263 ms和286 ms。由于数据经过主成分分析法降维，减少冗余信息，有效地降低了模型的识别时间，所以组合特征与单一特征模型的识别时间相差不大。

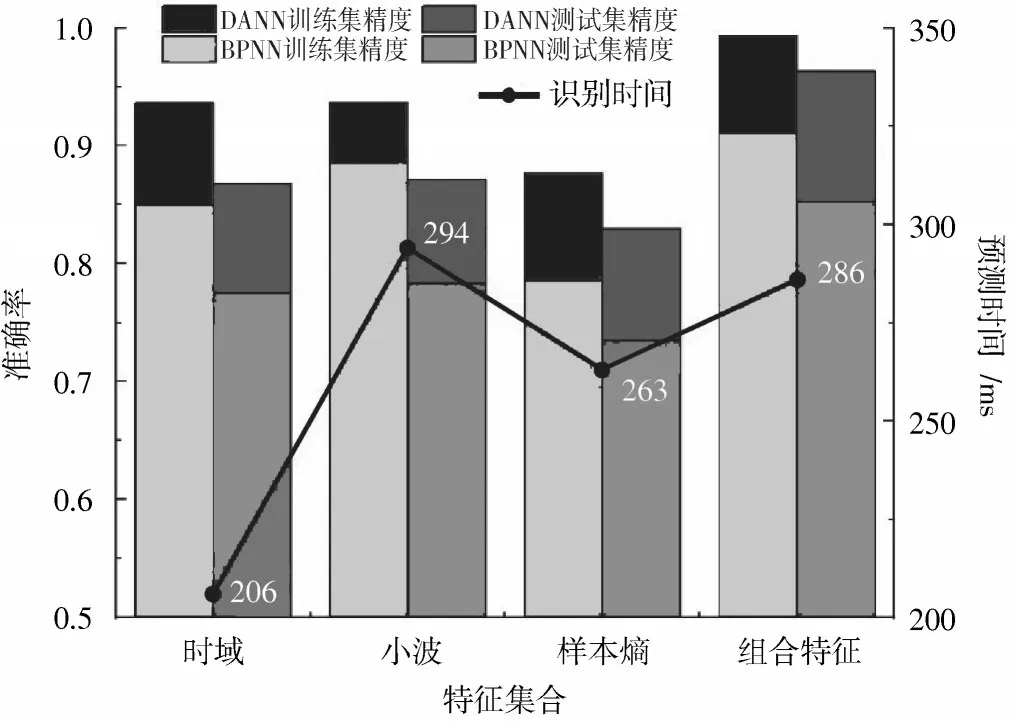
图9 改进神经网络与传统神经网络对比图

表2分别统计了在DANN模型中，不同特征的8种下肢运动意图识别准确率。由表2可知，直接利用时域特征进行下肢运动意图识别，平均识别准确率达到87.45%；通过分解小波子空间特征平均识别准确率为86.91%；使用样本熵作为特征对模型进行训练，模型的平均识别准确率只有83.5%；而优化组合特征作为动作识别样本的平均识别准确率可以达到94.89%。经过对比同一动作的识别准确率可知：时域特征对于坐下、站立、上楼梯和慢跑4个动作有很好的识别准确率，而在行走、左转和右转动作识别中的效果较差；小波分解特征对于上楼梯、下楼梯、左转、右转和慢跑的动作有良好的识别效果，小波分解子空间特征很好地弥补了时域特征左右转弯动作识别准确率低的缺点；而样本熵特征对于行走和上、下楼梯有较高的识别准确率。通过把三种特征融合，得到一个包含更加丰富信息的组合特征，从而提高了下肢运动意图识别准确率。

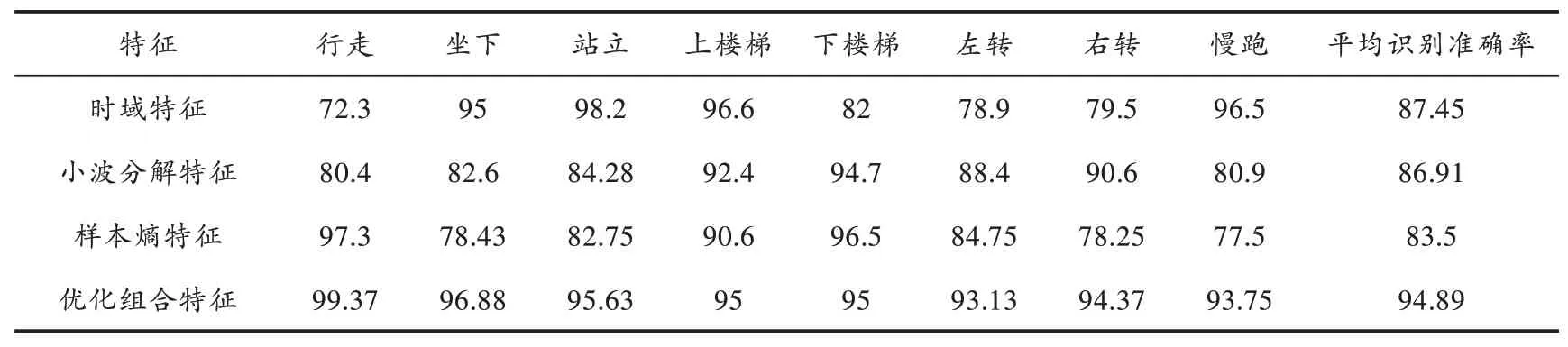
表2 不同特征的8种动作识别准确率 %

综合分析上述结果可知：使用主成分分析法有效地实现了特征向量的降维；通过使用改进的DE算法对下肢动作特征融合参数的优化，得到了一个包含更多信息的融合特征，解决了人工设置融合特征的参数效率低、难以得到最优权值参数的问题；最后，使用动态自适应神经网络模型对8种下肢运动意图识别，平均识别时间为280 ms，识别时间小于预期的300 ms，达到意图识别的目的，并且准确率可以达到94.89%。由此证明，基于sEMG多特征融合的动态自适应神经网络模型在下肢运动意图识别中取得了良好的效果。

5 结 语

为了保证运动识别的精度，很难实现一个模型精确识别所有受试者的动作，但对于体态特征相似的受试者可以增加训练的数据量实现下肢动作的识别。本文通过优化融合特征，使用动态自适应神经网络将基于sEMG的患者运动意图识别准确率提高到94.89%，证明了该方法的有效性，为穿戴式机器人的动作识别方法提供了参考。但本方法还存在一定的局限性，通过多特征融合后的模型，相比时域特征模型的实时性还需要进一步优化，继续完善不同年龄阶段受试者的数据库，提高模型的鲁棒性。

注：本文通讯作者为张峻霞。