基于演化博弈模型的本科生科研参与偏好研究
周 斌,赵昊骧,许玉久,陈佳佳
(1.新乡学院 经济学院,河南 新乡 453003;2.安徽大学 经济学院,安徽 合肥 230601)
教育部于2007年启动了“国家大学生创新性实验项目计划”,这一计划的实施对于激发大学生的创新潜质,培养大学生独立思考和解决问题的能力具有重要意义。2012年,教育部和中国科学院联合启动实施“科教结合协同育人”行动计划,强调了科技创新渗透于本科教学的重要性,将本科生科研训练纳入了新一轮的人才培养体系,努力培养一批具有科研潜质的优秀人才。在建设“新工科、新医科、新农科、新文科”的背景下,高校应主动地拥抱产业变革与科技创新的浪潮,培养具有高素质的优秀学生[1]。本科生参与科学研究是传统教学方式的拓展[2],它有助于培养他们独立思考的习惯,提高他们的科研素养和科研能力[3]。
就目前而言,面向大学生的学科竞赛很多,教师主持的研究项目也很多,但多数学生由于学习压力较大,科学研究意识比较淡薄,在参与学科竞赛或科学研究时迫切需要教师的指导[4]。教师在鼓励学生参与学科竞赛的同时,要引导学生参与项目研究。由于学生人数众多,学院很难了解每个学生的真实科研能力,这就容易导致部分研究能力较弱的学生参与了难度较高的项目,而研究能力较强的学生参与了难度较低的项目。为了解决这一问题,我们在考虑参与风险与收益的前提下,构建以学院和学生作为主体的动态博弈模型,基于双方的决策期望收益,根据博弈主体的复制者动态方程得到了演化博弈系统的渐进稳定性条件和各均衡点坐标,讨论了3种不同的均衡点的稳定性并进行了数据仿真,为准确引导学生参与学科竞赛和科学研究提供参考。
1 演化博弈理论与收益矩阵
演化博弈模型的先行条件是决策者的有限理性,即决策者在决策过程中通过不断试错寻求最优策略。在信息不完全环境中,决策双方在寻求决策过程中的策略在不断变化,因此博弈双方不可能一次找到均衡点,他们需要对决策行为进行不断的修正,以达到在既定成本不变时利益最大化或决策最优的目的[5–6]。由于学生与学院都无法一次性找到最有效的决策方案,学院需要通过不断地组织学科竞赛来知悉学生的决策意图,了解学生的能力与喜好,学生也需要知悉学院对项目的评估结果与扶持力度。
根据以上分析我们作如下假设:1)面对学科竞赛或科研项目,学生面临两种决择,一是选择难度和科技含量较高的(下称A类)项目,二是选择难度和科技含量较低的(下称B类)项目。由于学生精力有限,他们只能参与一个项目。2)面对学科竞赛或科研项目,学院面临两种决择,一是扶持学生参与A类项目,二是扶持学生参与B类项目。由于条件限制,学院只能选择一类项目。3)为了提高学生的积极性,学院无差异地鼓励所有学生参与。4)学生参加任意一类项目,总能获得一定的成果,学院扶持任意一类项目,总能获得一定的成果。
当学生选择参与A类项目,学院重点扶持A类项目时,学生的最大收益为ra,学院的最大收益为ca,但
A类项目有一定技术含量,且以概率p产生不必要的额外成本e。当学生选择参与B类项目,学院重点扶持A类项目时,学生的最大收益变为rb,学院的最大收益变为cb,但由于学院重点扶持A类项目,额外成本依然存在。当学生选择参与A类项目,学院
选择扶持B类项目时,由于学生未能得到学院的扶持,无法完成难度高的项目,故收益为0,而学院能获得参与B类项目的成果收益c0。当学院选择扶持B类项目,学生选择参与B类项目时,学生能够获得最基本的收益r0,学院也能获得最基础的收益c0。根据以上分析可得如表1所示的博弈收益矩阵。

表1 参与项目的博弈收益矩阵
2 动态演化博弈模型的构建与求解
在实际操作中,通常会出现以下情况:学院不会公开项目的难易程度,而是无差异地鼓励学生参与,学生无法了解项目的难易程度;学生为了获得参与的机会,可能会过分包装自己,学院无法知道学生的真实水平。学院和学生在决策前都有自己的预期,但双方的预期决策无法被对方察觉,因此双方就会做出混合策略,即在一定概率条件下准备不同的选择,以实现策略的均衡,此时任何一方改变策略都不会增加额外收益,因此可建立动态演化博弈模型。
假设学生以概率x选择参与A项目,以概率(1 −x)参加B项目,假设学院以概率y扶持A项目,以概率 (1 −y)扶持B项目,则选择参加A类和B类项目的学生的收益分别为
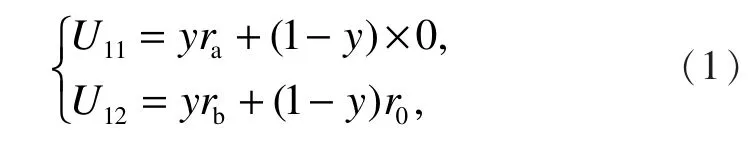
学生的期望收益为

同理,选择扶持A类和B类项目时,学院的收益分别为
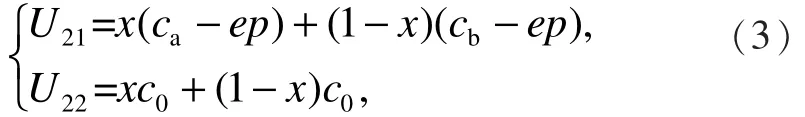
学院的期望收益为

由以上推导可知,学生与学院的复制者动态方程组为
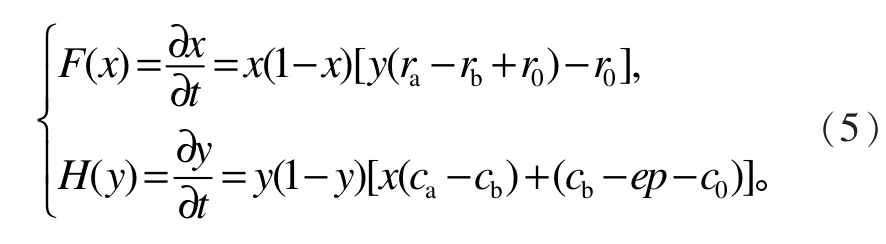
下面分析学院与学生两个主体的决策均衡点。在稳定状态下,均衡点要具有稳健性与抗干扰性,即行为主体选择确定的最优稳定策略才是演化稳定策略(ESS)。在博弈中,最优策略是指任何行为主体改变策略都是无利可图的,而稳定策略则是指任何细小的扰动都不影响最终决策结果,即演化博弈的均衡点不受随机因素干扰。
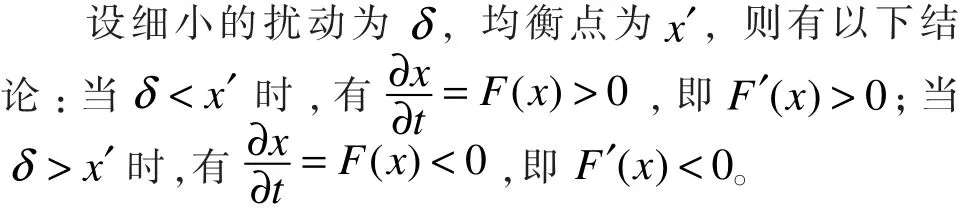
对方程组(5)的第一式求x的偏导数,第二式求y的偏导数,并令它们等于零,有

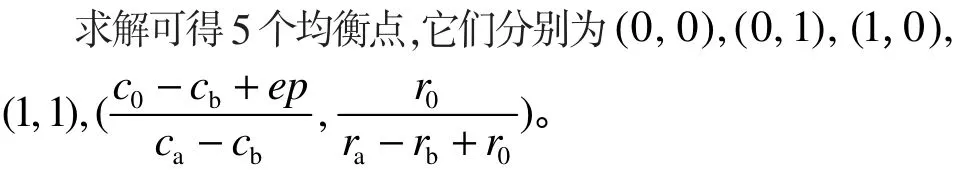
由方程组(5)可得其相应的雅可比矩阵
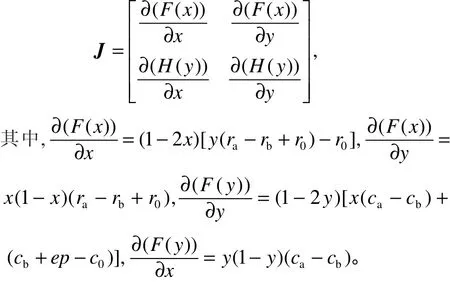
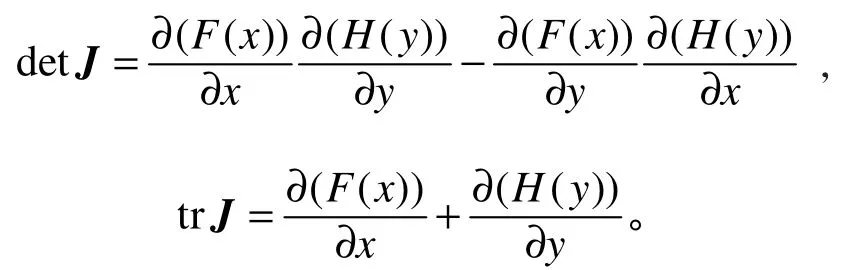
雅可比矩阵的行列式和迹分别为各均衡点对应的行列式和迹由表2给出。

表2 各均衡点的行列式和迹
均衡点局部稳定条件为 detJ> 0,trJ<0。此时的均衡点即是稳定策略。通过符号的判断可知ra>rb>r0,0
情形1:当c0−(cb−ep) <0,决策点坐标不在策略空间内,此时均衡点的稳定状态见表3。
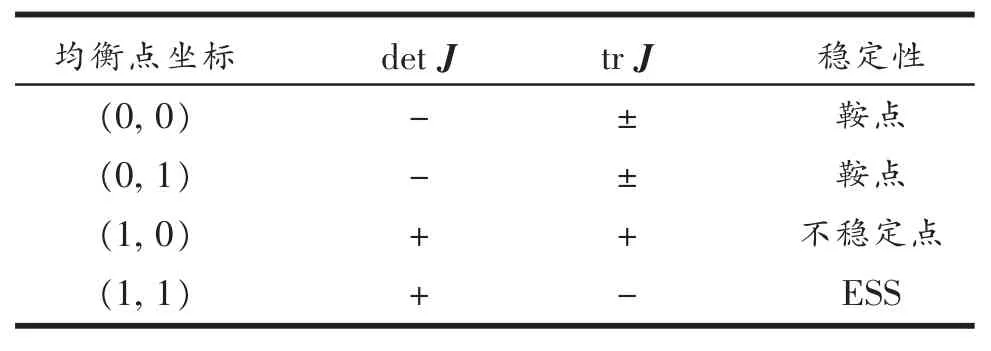
表3 情形1时均衡点的稳定状态
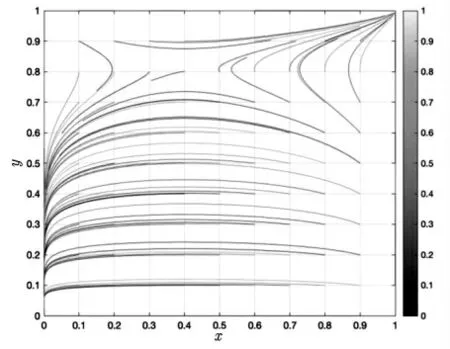
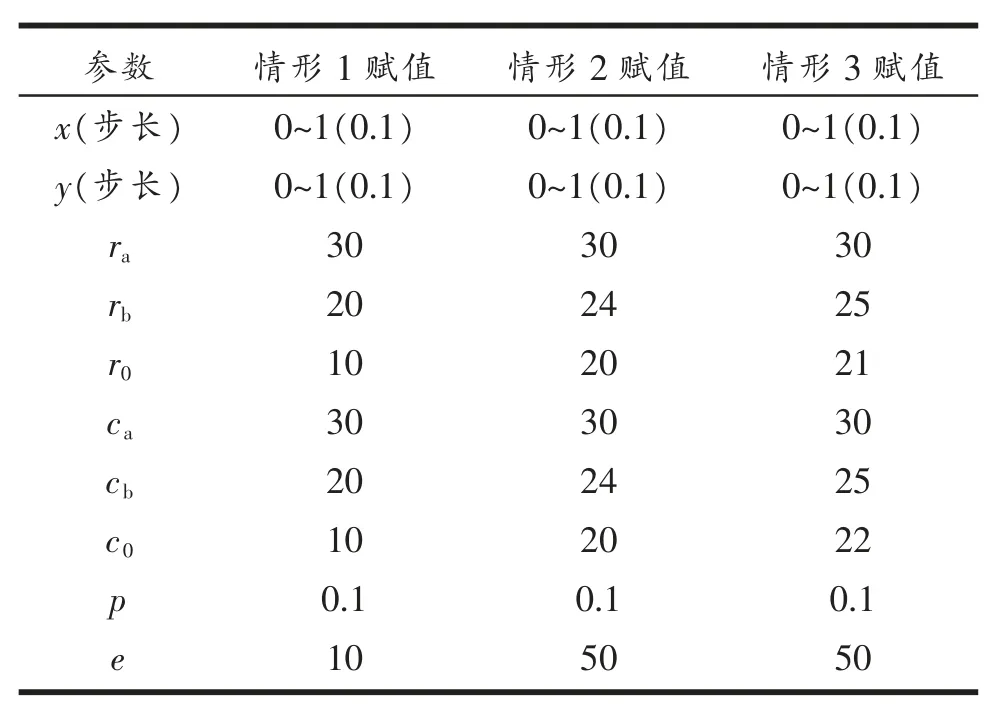
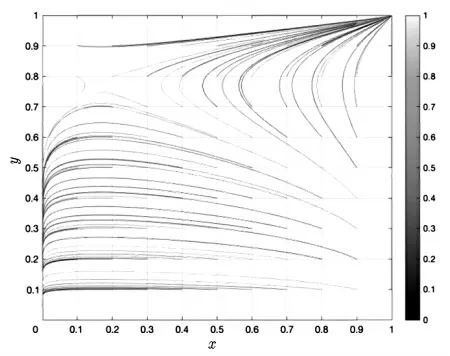
情形2:当 0 表4 情形2时均衡点的稳定状态 情 形3:当c0−(cb−ep) >(ca−cb),决 策 点 坐 标不在策略空间内,此时均衡点的稳定状态见表5。 表5 情形3时均衡点的稳定状态 下面对各均衡点的稳定性进行分析。 当c0−(cb−ep)<0时,扶持A类项目的收益大于扶持B类项目的收益,学院选择激进决策,扶持A类项目。此时学生无论参与A类项目还是B类项目都能获得一定收益,学院也能获得更高的收益。 当0 当项目难度较低时,学院更倾向扶持A类。 当c0−(cb−ep) >(ca−cb)时,扶持A类项目收益大于扶持B类项目,此时学院选择保守决策,扶持B类项目,此时学生参与B类项目能够获得稳定收益,参与A类项目无法获得收益。 由以上3种情形可知,学生参与科学研究与学院扶持之间博弈存在最终稳定策略,但行为主体在实现最终行为决策前的博弈过程以及策略变化轨迹无法直观刻画,因此借助Matlab2020对变化路程、变化速度进行了仿真,仿真参数设置见表6,仿真结果见图1、图2和图3。 图2 情形2的仿真结果 图3 情形3的仿真结果 表6 仿真参数的设置 图1 情形1的仿真结果 由以上结果可知,大部分学生在做科研参与决策时,选择项目类别的依据在很大程度上取决于学院对参与收益的评估。当学院认为A类项目的收益远大于B类项目时,学院更愿意扶持参加A类项目的学生,此时学生的最优策略就是参与A类项目。同样,当学院认为A类项目收益与风险损失之和小于B类项目收益时,学院就会选择扶持B类项目,此时学生为了获得收益,就会选择B类项目。 当学院无法准确做出项目的收益评估时,风险损失就成为决策的主要依据。当项目的风险较高时学院则会趋于保守,当风险较低时学校就会趋于激进,这符合前两类决策依据。此时学生是相对被动的,他们需要考虑学院的认可,并在此基础上确定自身的最优策略。可能的后果是有的学生为了获得更高的收益而盲目参与A类项目的研究,且没有取得什么成果,另一些有能力的学生由于得不到学院的支持而参与B类项目的研究,从而失去获得更高收益的机会。 在扶持项目时,学院不能只注重科研项目带来的收益,而需要结合学生的参与意愿和能力综合研判。在一定情况下,适当放弃部分收益也是一种决策。对于一些难度大、成果转化率低的项目,可先对学生的能力进行评估及调查,当参与该类项目研究的学生的能力尚未到达预期时,如果扶持难度高的项目,成本风险会被放大,学院应当采取较为保守的决策,扶持难度较低的项目。同样,如果学生的能力普遍较强、素养较高,获得高收益的成本风险就会大大降低,学院扶持这类项目才是整体上的最优决策。学院和学生不能盲目求高,也不能过分保守。学院应对参与项目的学生有一定的了解,而不应对学生进行无差异选拔,否则就可能把项目与学生错配,无法获得最佳收益。因此,教师应将项目融入教学过程,提升学生的学术思维与科研素养水平,引导学生参与感兴趣的项目,这样学生在选择科研项目时才能更加理性,参与科研项目研究更加高效。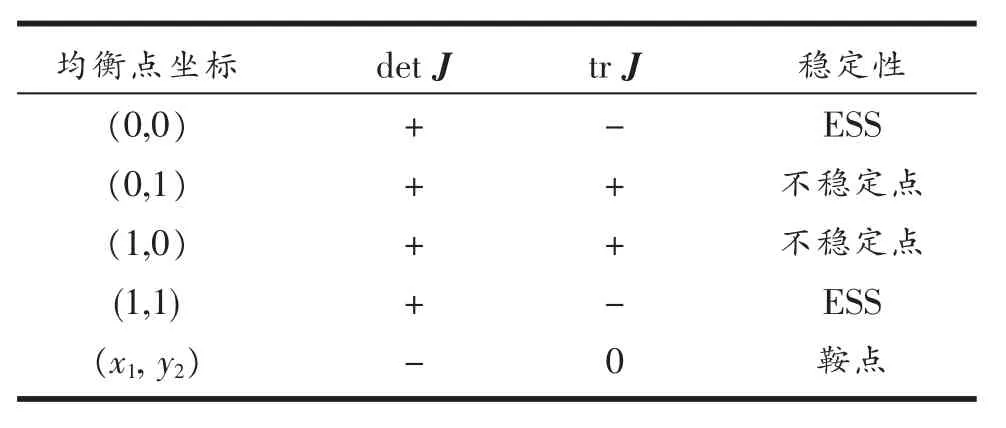


3 结果分析与建议

