基于模型修正理论的装配式梁桥载荷横向分布计算

李 院 军

(广东省交通规划设计研究院集团股份有限公司 第四设计院, 广东 广州 510507)

在桥梁使用年限增加、交通量增长及外界环境变化的多重压力下,装配式梁桥的主梁和横向联系结构病害问题日益突出[1-3]。载荷横向分布系数通常用来衡量桥梁横向传力能力。原有计算桥梁载荷横向分布系数的方法是基于桥梁未发生损伤的理想状态,反映结构特性的参数也是计算值,而当结构发生损伤后,其结构的特性参数已经发生变化,若继续用原来的理论计算值去计算,则结果会失真,故桥梁发生损伤后的相关参数的确定及载荷横向分布系数的计算问题亟须解决。

目前,Russo[4]开展了桥梁损伤后强度和载荷分布特性的评估研究。由建立的损伤模型得知,损伤梁中的弯矩显著减小,载荷重新分布到相邻的主梁上。Lantsoght[5]为了研究载荷横向重分布问题,对靠近支座的集中载荷作用下的构件进行了试验研究。Razaqpur[6]采用非线性有限元法研究了混凝土非线性和钢材屈服对简支组合梁桥载荷分布的影响。国内外学者也做了许多有益的工作,刘华等[7]为了得到一种新的计算桥梁载荷横向分布的方法,以动力参数与主梁挠度的关系为出发点,选取了模态质量、频率和振型做为参数进行理论推导。李院军等[8]考虑桥梁在役期间梁体的损伤,提出了考虑主梁损伤的装配式梁桥载荷横向分布计算的理论方法。聂鑫[9]为了研究变截面组合箱梁桥的载荷横向分布规律,同时考虑其主梁抗扭刚度,分别采用杠杆原理法、修正刚性横梁法及有限元法进行对比分析。成琛等[10]提出了考虑铰缝损伤的铰接板法计算模型,并讨论了不同损伤位置和损伤程度对横向分布系数的影响。其他学者还在载荷横向分布系数的数值模拟、理论修正和试验上做了相应的研究[11-12]。然而上述研究,虽然涉及了桥梁发生损伤后的载荷横向分布系数研究,但损伤参数的确定往往较难量化,且使用模型修正理论对损伤参数进行修正的人更少。使用模型修正理论对损伤参数进行修正会使计算模型更加接近真实的受力情况。

本文以比拟正交异性板法为基础,提出考虑桥梁损伤的计算模型。基于模型修正理论对计算模型进行修正:首先确定待识别参数,并选择动力的多目标函数;再通过L-M法对目标函数进行优化;最终得到修正后的参数。将修正后的参数代入计算模型,便得到了一种考虑桥梁损伤的载荷横向分布系数的计算方法。

1 比拟正交异性板挠曲微分方程的建立

在役梁桥中,主梁和横向联系结构的损伤会对载荷横向分布系数产生影响,横向联系结构一般包括桥面板(翼缘板)横向接缝和横隔梁。对于装配式梁桥,主梁和横向联系结构的损伤分别通过对主梁抗弯刚度、抗扭刚度、横向联系构件的抗弯刚度和抗扭刚度的折减来考虑。因此,可以得到考虑桥梁损伤的修正载荷横向分布系数计算模型。

由内力与载荷、位移和应变的平衡关系可以得出[13]

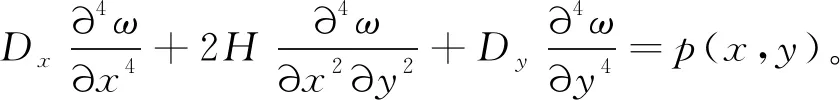
(1)

式中:ω为单位载荷作用下比拟板任意一点的挠度值;p(x,y)为作用在比拟板任意一点的外载荷;Dx、Dy为板在x和y两个方向的单宽抗弯刚度;H=D1+Dxy,D1为单宽相关抗弯刚度,Dxy为单宽抗扭刚度。

在图1中,主梁间距为b,每片主梁的截面抗弯惯性矩和抗扭惯性矩分别为Ix和IT x;横隔梁的间距为a,其截面抗弯惯性矩和抗扭惯性矩分别为Iy和IT y。换算后的比拟正交异性板其在纵横向单宽度的截面抗弯惯性矩和抗扭惯性矩分别为

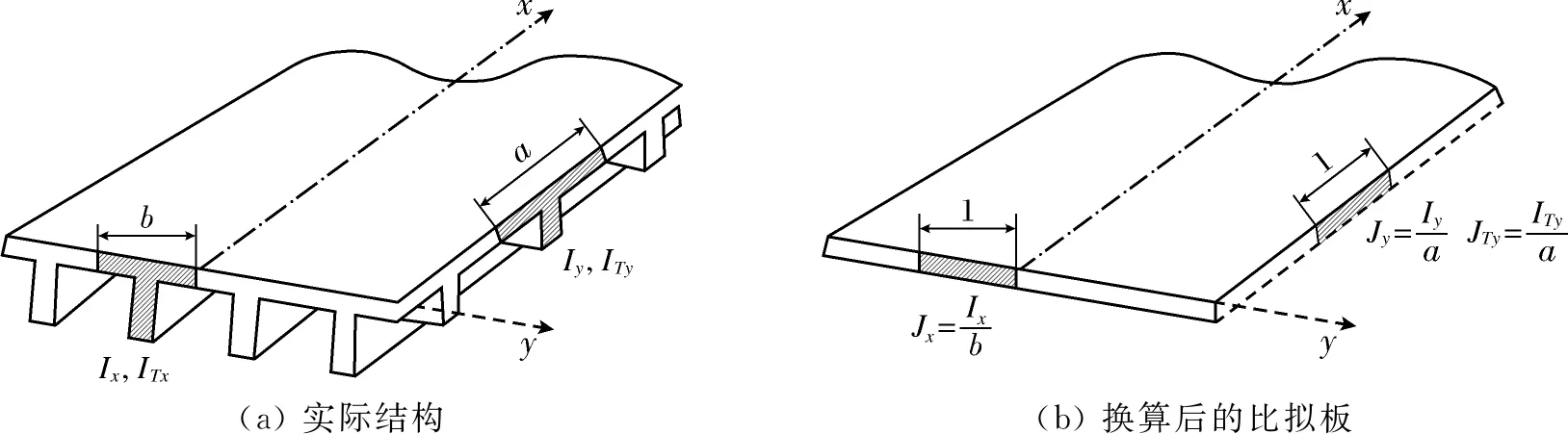
图1 多梁式结构比拟正交异性板换算

(2)

再将式(2)中的关系式代入式(1),便可以得到多梁式比拟正交异性板的挠曲微分方程

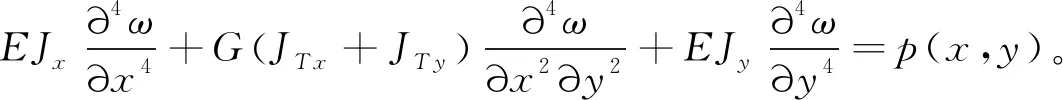
(3)

式中:E为材料的弹性模量。

2 基于静力的模型修正法

结构静力模型修正是利用结构静力测试响应信息,通过各种方法使结构静力响应的理论值与实测值尽可能一致,从而得到修正后结构模型参数。

2.1 识别参数

在使用年限和交通量增长的双重压力下,装配式梁桥的主梁、横向联系构件必然会出现不同程度的损伤,由公式(3)可知装配式梁桥发生损伤后,其计算模型的主梁单宽抗弯刚度EJx、单宽抗扭刚度GJT x和横桥向的单宽抗弯刚度EJy、单宽抗扭刚度GJT y均需要修正,以达到模拟真实桥梁的受力和使用状态。由此可以得到结构发生损伤后的比拟正交异性板挠曲微分方程

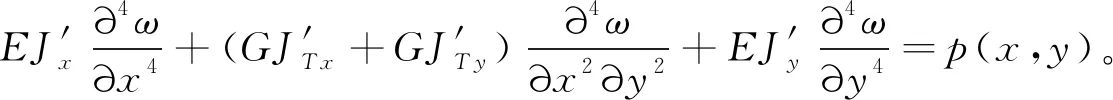
(4)

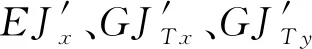
2.2 构造目标函数

根据结构类型、试验工况以及测量响应不同,选择静力位移,即每片梁的挠度值来构造目标函数

(5)

式中:F(X)为基于静力响应的目标函数;Ut i是现场试验的实测挠度值;Ua i是结构理论模型计算的挠度值;n为载荷试验中挠度测试点数量。

为了使结构理论模型的计算挠度值与载荷试验测试挠度值的差异最小,即求解最小值问题。

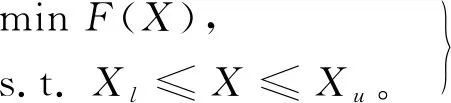
(6)

式中:X为待修正的结构模型参数集;Xl、Xu为结构模型参数集X的下限和上限,是优化问题的约束条件。

2.3 模型修正过程

目标函数求解是一个不断寻优的过程,本文使用L-M法对目标函数进行优化,两者能够各自吸取优点进行综合运算,快速和准确的迭代计算方法,整个优化计算通过MATLAB自编程序实现[14]。

模型修正主要分为3个主要的步骤:①基于比拟正交异性板法建立考虑桥梁纵横构件损伤模型,该损伤理论模型主要是用于迭代运算;②选择待识别的参数,并基于静力参数构造目标函数,在相应的约束条件下,目标函数取得最小值,即是一个最优化过程。③运用L-M法对目标函数进行优化,该方法加快了运算的过程,这步骤是采用数学工具对待修正参数的求解过程。模型优化流程如图2所示,具体的修正过程如下:

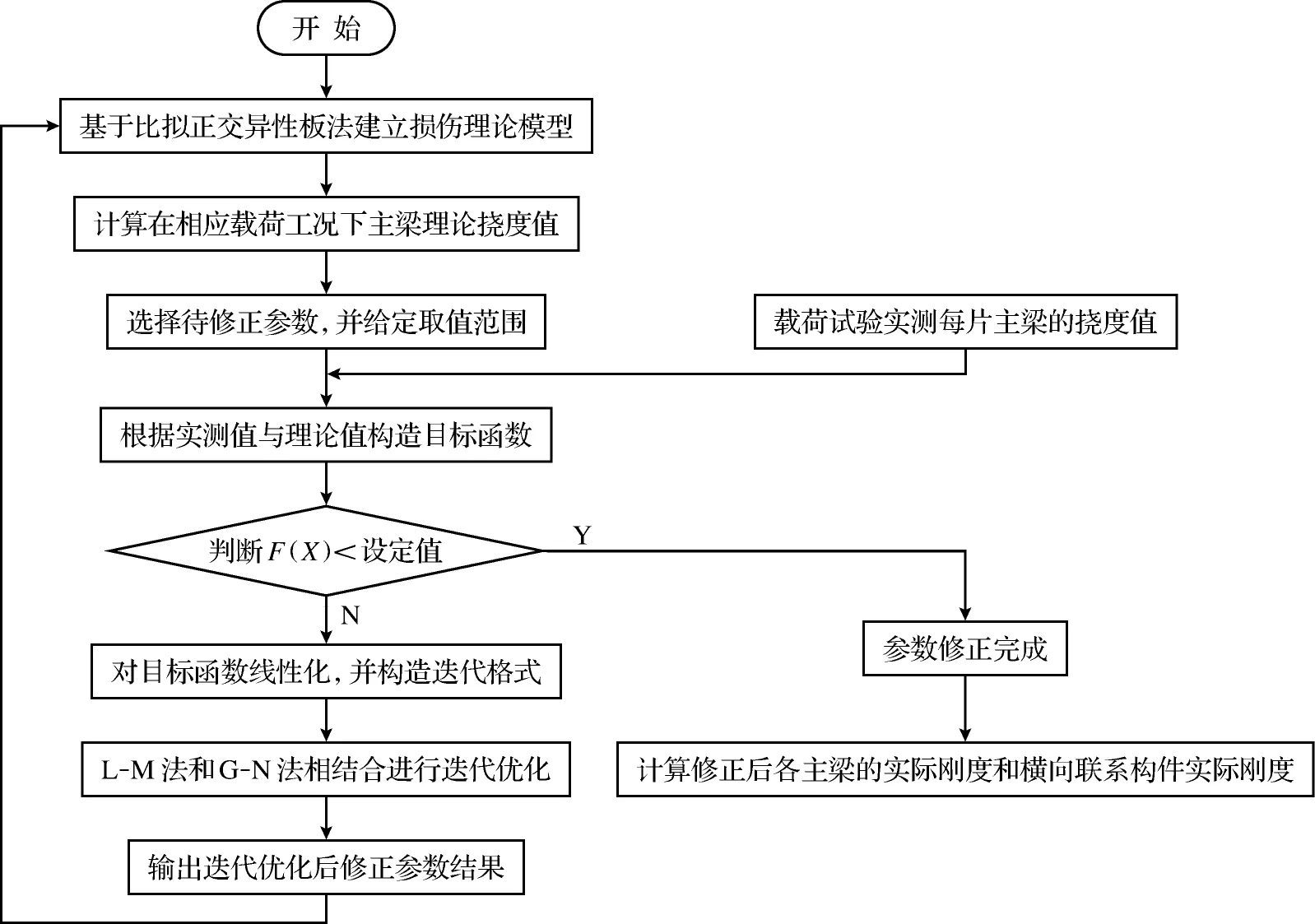
图2 模型优化流程图

1) 建立损伤理论模型。基于比拟正交异性板法,考虑纵向主梁和横向联系构件的损伤,最终建立损伤理论模型,如式(4)。并根据桥梁的载荷试验加载工况,通过式(4)计算各片梁跨中挠度值。

2) 选择修正参数。选择主梁单宽抗弯刚度EJx、单宽抗扭刚度GJT x和横桥向的单宽抗弯刚度EJy、单宽抗扭刚度GJT y,再分别对相应的系数范围做出规定。

3) 基于静力参数构造目标函数。由主梁实测挠度值与损伤模型的理论计算值来构造目标函数,如式(5)。判断目标函数值是否小于设定误差值,如果小于则输出模型修正结果,并计算修正后参数值,反之,则进入下一步,采用算法优化修正。

4) L-M法优化目标函数。对目标函数进行线性化,在点Xk对F(X)进行一阶泰勒展开,并进行不断的迭代,输出修正结果,代入第一步损伤理论模型,如此反复循环,直到满足F(X)小于设定值。

3 载荷横向分布系数的计算

根据静力模型修正法对4个识别参数分别进行修正,再把修正后的结构刚度值代入式(3),便可根据挠度值与载荷横向影响线的关系,得到模型修正后的每片梁载荷横向分布系数,具体过程如下。

根据载荷和挠度成正比的关系[13],有下式成立:

(7)

式中:η1k,η2k,η3k,…,ηn k为在k点作用单位载荷下各板条所承担受弯载荷;C为与跨径和截面特性相关的常数。

由图3的几何关系,可得到下式:

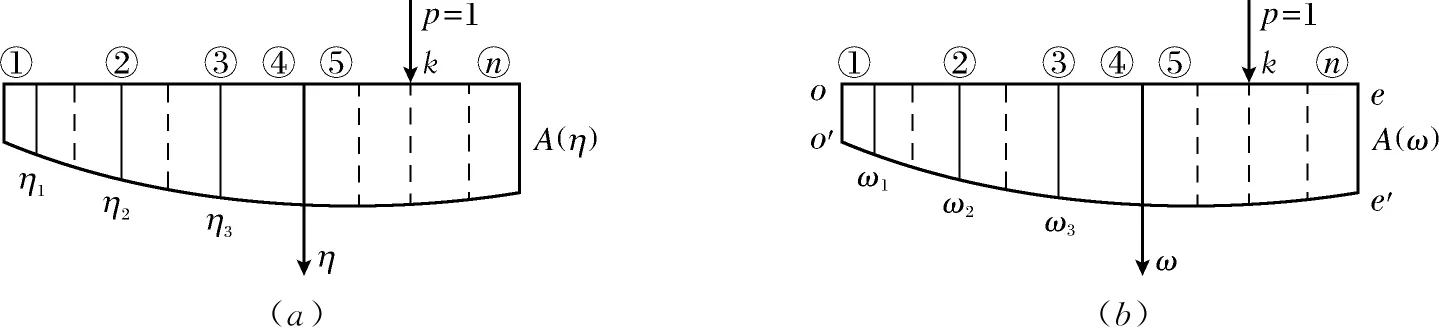
图3 横向挠度和横向影响线竖标值

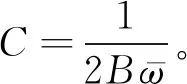
(8)

根据式(8)求得的常数关系式,则各板条所承担的载荷峰值ηi k可表示为

(9)

将任意一点的挠度值与同样载荷作用下的平均挠度值之比定义为影响系数Kk i,同时根据功的互等原理,即ηi k=ηk i,可得

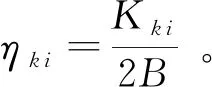
(10)

通过式(10)便可得出主梁横向影响线,并通过最不利加载,得到主梁载荷横向分布系数。

4 实例验证

4.1 工程概况

以某(左幅)装配式小箱梁桥为例,把模型修正后的计算结果与实桥数据进行对比。

该桥于2004年建成,全长为206.6 m。上部结构采用10 m×20 m预应力混凝土连续箱梁;预制装配式梁间距3.067 m,梁高1.2 m,跨中横断面布置如图4所示。

图4 跨中横断面布置(单位:mm)

试验检测前后对试验跨主梁主要受力部位进行检查,试验跨4片主梁腹板均有竖向裂缝,裂缝长度为3～11 cm,宽度为0.2 mm左右,同时3条桥面接缝也出现较长开裂的现象。

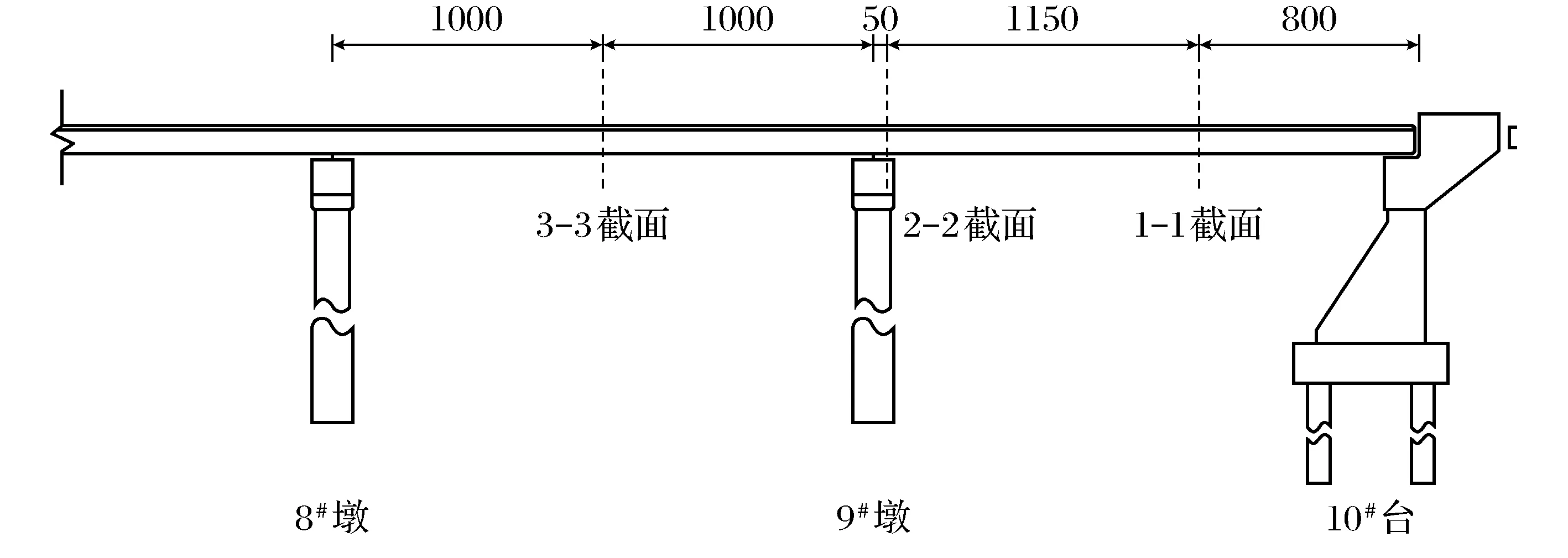
图5 测试截面位置(单位:cm)

图6 静载试验加载

4.2 模型修正结果

表1为模型修正前后挠度值计算值与实测值对比,可以看出,当结构发生损伤后,损伤的主梁误差较小,这是由于主梁损伤后挠度值表达,而没有损伤的主梁,则挠度计算值与测点的实测值相比误差较大,误差极值为16.4%,远远超出规范的允许误差范围,表明桥梁的实际受力情况与设计状态发生了偏差,需要对相应的参数进行修正。而模型修正后的整体挠度计算值与实测值吻合度较高,误差范围在3.6%～5.0%之间,满足工程允许范围,表明本文的修正模型的正确性。

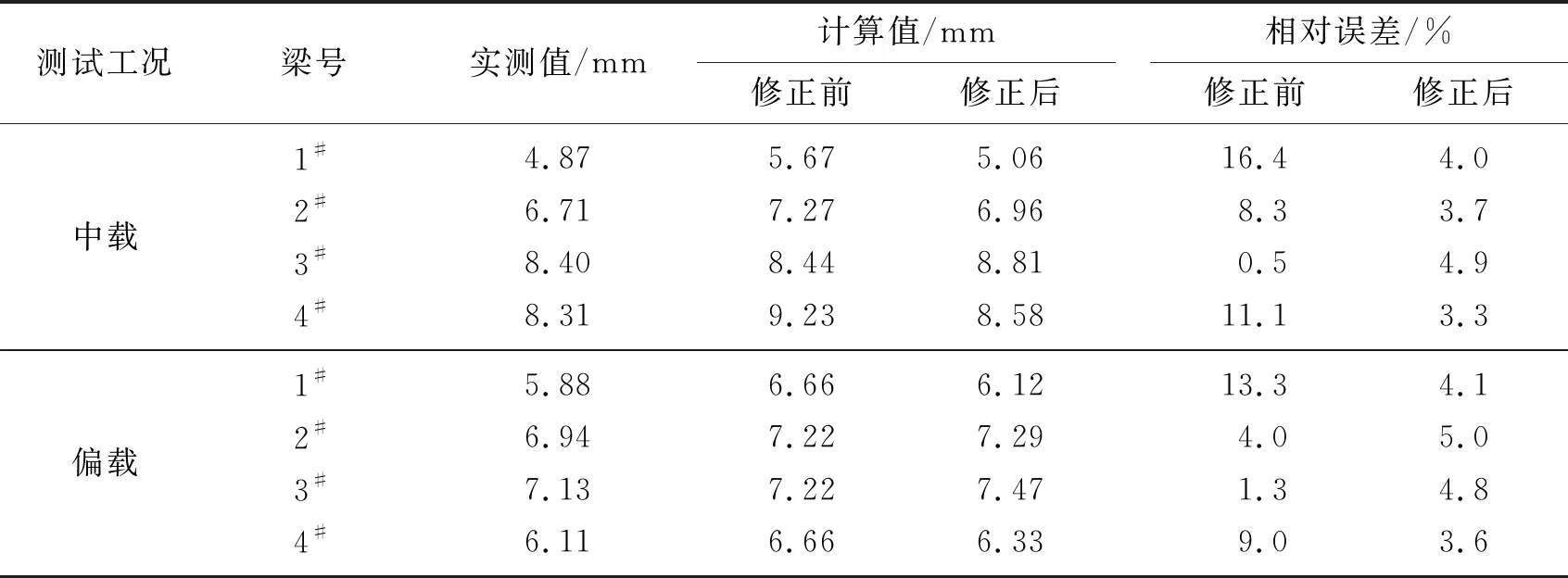
表1 模型修正前后挠度值对比

从表2的修正结果可知,横桥向单宽抗弯刚度折减最大,下降了70.2%,横桥向单宽抗扭刚度次之,下降了52.9%,主梁单宽抗弯刚度也下降了14.2%,主梁单宽抗扭刚度也下降了12.5%。表明该桥的横向损伤情况大于纵向,亟须对横向联系进行维修加固。

表2 模型参数修正前后对比

4.3 载荷横向分布系数计算

根据前面得到的关于桥梁刚度的4个识别参数修正后的数值,分别代入式(3),并通过主梁横向影响线与载荷横向分布系数的关系,最终得到每一片主梁的载荷横向分布系数。根据载荷试验的每片梁的实测数据,也可得到主梁实测载荷横向分布系数[15]。具体结果见表3和图7。

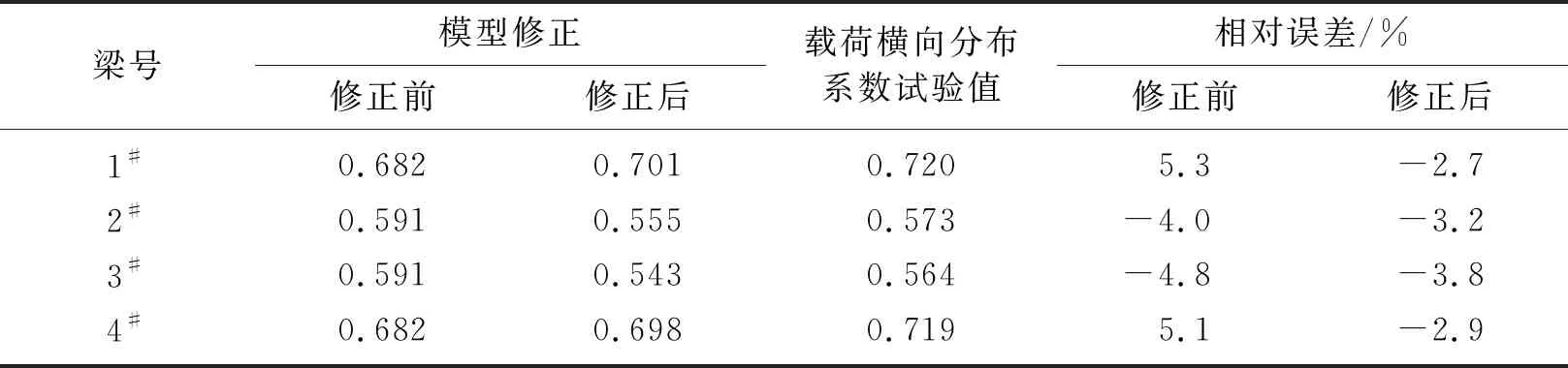
表3 载荷横向分布系数修正前后对比

从图7的2片梁横向影响线图可以看出,模型修正后计算所得的影响线与实测值影响线吻合度较好,误差较小,而模型未修正数据则与实测数据偏差较大,如果不对模型进行修正,则计算结果将明显失真。按照规范进行最不利加载,得到主梁跨中截面载荷横向分布系数,具体数值如表3所示,可知模型修正前各片梁的载荷横向分布系数与实测值相对误差较大,而模型修正后的主梁载荷横向分布系数与实测值误差较小,从而验证了模型的合理性与可靠性。

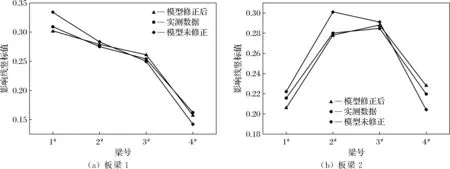
图7 横向影响线对比

5 结 论

1) 本文在比拟正交异性板法的基础上,建立了一个考虑桥梁纵横向发生损伤的计算模型,通过模型确定了主梁单宽抗弯刚度EJx、单宽抗扭刚度GJT x和横桥向的单宽抗弯刚度EJy、单宽抗扭刚度GJT y4个待修正参数,桥梁损伤越严重,其修正的数值范围越大。

2) 采用L-M法对目标函数进行迭代优化,模型迭代次数相比于传统的数值迭代明显减少,提高了计算效率。

3) 通过工程实例验证。结果表明:模型修正后的挠度计算值与实测值吻合度较高,误差范围在3.3%～5.0%之间;各修正参数皆发生了损伤,其中横桥向单宽抗弯刚度折减最大,下降了70.2%,横桥向单宽抗扭刚度次之,下降了52.9%,主梁单宽抗弯刚度下降了14.2%,主梁单宽抗扭刚度下降了12.5%;模型修正后的主梁载荷横向分布系数与实测值误差较小,误差绝对值小于3.8%,说明本文的计算方法具有较高的准确性。