一种经验模态分解与深度神经网络协作的短时电力负荷预测方法

邓真平

(重庆市科源能源技术发展有限公司，重庆 渝北 401147)

0 引言

电力负荷预测要依据历史负荷数据及其影响因素.对于电力生产单位而言，准确的负荷预测不仅对场站发电计划、机组启停计划、检修计划制定至关重要，对于保障发电侧与用电侧的平稳运行，降低发电成本，提高经济效益和社会效益也具有重要意义[1-2].负荷预测依据时间维度可以划分为短时预测、中期预测、长期预测[3].依据预测输出维度，可划分为单点预测、多点预测、曲线预测.其中，单点预测以当前时刻为起点，基于历史数据和影响因素对下一时刻的负荷值进行预测输出，多点预测对未来多个时刻点的负荷值一次性输出其预测值.曲线预测在多点预测的基础上，对未来更多时刻点的负荷进行预测，以便依据足够的负荷走势，对发电计划作出调整.目前，在电力市场中常要求以15分钟为间隔对每日96点负荷曲线进行预测输出.

围绕电力负荷预测，研究者从不同角度进行了研究，目前主要集中在灰色模型、时序模型、神经网络模型等模型的构建及其优化方面，并取得较多研究成果.例如，王丽[4]等针对中长期日负荷曲线的预测问题，考虑不同产业结构用电需求、经济发展对电力负荷的影响，构建了一种灰色神经网络模型，并通过粒子群算法对预测模型的权值和阈值进行寻优，从而缩减参数的搜索范围，以提高日负荷曲线预测效率.崔和瑞[5]等运用协整理论，考虑“温度”等因素对预测结果的影响，以弥补传统时序分析对显著性外界因素考虑的不足.在此基础上，利用SAS软件构建负荷序列与“温度”之间的ARIMAX模型，提高了对具有突变结构的负荷时序的预测精度.解加盈[6]等通过引入偏最小二乘法，首先在数据层面分析了输出功率与变量因素之间的关系，在此基础上利用交叉有效性原则和投影重要性指标对变量进行降维处理，将优化后的变量子集输入到深度神经网络(Deep Neural Network，DNN)模型，从而实现对风电机组功率曲线的预测.董浩[7]等通过核主成分分析方法对负荷预测因素进行降维处理，将降维后的变量输入到极限学习机，实现了一天连续24点预测.

值得指出的是，虽然电力负荷时序在一定条件下整体呈现平稳性，但是受天气、季节、节假日等因素影响，往往也会表现出波动性.对于非平稳负荷的预测，传统算法虽然在一定程度上也可以实现对负荷的单点、多点或者曲线预测，但是预测效果难以保证.为了克服对非平稳负荷序列的预测问题，研究者从时序分解的角度进行了研究.邓翱[8]等在经验模态分解(Empirical Mode Decomposition，EMD)的基础上，分析各随机、周期、趋势分量与影响因素之间的关联，从而挖掘出负荷序列的波动机理.魏骜[9]等针对电力负荷序列的非线性、非平稳性等特点，通过EMD算法对负荷时序进行分解以降低序列的非平稳性，然后将分解后的序列输入到长短期记忆(long short-term memory，LSTM)网络，对各预测分量进行重组后得到预测结果.陈艳平[10]等在对负荷序列做EEMD分解后，通过样本熵对各分量进行复杂度分析并产生新的子序列，利用Elman递归神经网络模型对各子序列进行预测并叠加得到最终负荷预测结果.

上述研究面向负荷预测不同时间尺度、不同输出维度需求并基于不同的理论模型进行了研究，为负荷预测问题的解决提供了新研究思路.但在实际应用中不仅要求对负荷进行不同时间尺度的预测，还要求能对未来连续多日的负荷曲线进行预测.基于此，本文提出了一种基于EMD与DNN协作的短时电力负荷预测方法，在EMD分解的基础上，建立各分量的DNN预测模型，实现以15分钟为间隔对未来连续7日的负荷曲线的预测.

1 EMD与DNN基本原理

1.1 EMD基本原理

EMD算法作为一种信号处理方法，从信号序列本身的尺度特征出发对信号分解，得到代表原始负荷数据中隐含的不同时间尺度的波动成分，即本征模式分量(Intrinsic Mode Function，IMF)，以弱化原始信号的非平稳特性.分解后的剩余残差项则表示负荷序列的基本趋势[11-13].

文献[14-15]指出，由EMD分解得到的各IMF分量必须满足约束条件，即分量序列中极值点与过零点的数目最多相差一个，同时由局部极大值和局部极小值确定的上下包络线的均值为零.若电力负荷序列为x(t)，则EMD的分解步骤概括如下：

Step 1：利用三次样条差值法分别对x(t)的局部极大值点和极小值点进行拟合，得到上包络线Us(t)和下包络线Vs(t).

Step 2：计算Us(t)和Vs(t)的包络均值m1和信号剩余分量h1，即：

(1)

h1=x(t)-m1

(2)

Step 3：若h1满足IMF分量约束条件，则h1为第一个IMF分量；反之，对h1重复Step 1 ～ Step 2，直至h1满足约束条件，记imf1=h1.

Step 4：计算残余信号r1=x(t)-h1，重复Step 1 ～ Step 3，直至分解出n个IMF分量.

Step 5：记分解n个IMF分量后，原始信号的剩余信号残差为：

rn=rn-1-imfn

(3)

相应的，原始负荷序列与IMF分量、信号残差之间满足：

(4)

1.2 DNN基本原理

DNN模型是具有多层和一定深度的神经网络模型，广泛应用于非线性系统建模[16-17].在输入信号的前向传递中，通过隐藏层之间的连接、权值、阈值、激活函数，逐层计算输入信号，得到输出值.若输出结果与目标值不满足误差约束，则通过反向传播调整各层网络权值和阈值，使网络输出逼近预期值.图1为DNN的一般拓扑结构图，其中X={x1,x2,…,xm}为网络的输入序列，Y={y1,y2,…,yn}为网络的输出序列.DNN网络的使用一般包含两个基本过程，即训练过程和测试过程.通过训练过程，标定满足当前训练数据网络各层节点之间的权值和阈值.通过测试过程对未来时刻或时间段进行预测输出.DNN的训练步骤概括如下[16,18-19]：

图1 深度神经网络拓扑结构

Step 1：根据训练输入和输出数据，确定网络模型的隐藏层数L和各层的网络节点数pl(l=1,2，…，L)，随机初始化各隐层和输出层之间的权值Wl和偏移向量bl(l=2,3,…，L)，学习率η，迭代阈值ε，神经元激活函数f(·).

Step 2：计算隐藏层和输出层输出Hl.

Hl=f(zl)=f(WlYl-1+bl),l=2,3,…，L

(5)

式(5)中，f(·)为隐藏层和输出层的输出激活函数.典型的激活函数有ReLU函数、tanh函数，其表达式如式(6)～(7).

f(x)=max(0,x)

(6)

f(x)=(ex-e-x)/(ex+e-x)

(7)

Step 3：根据损失函数计算输出层的梯度δL，损失函数和梯度计算如式(8)～(9).

(8)

δL=J(W,b,X,Y)⊗f＇(zL)

(9)

Step 4：计算各隐层的梯度δl.

δl=(Wl+1)Tδl+1⊗f＇(zl),l=L-1,L-2,…，2

(10)

Step 5：根据本次网络输出和期望值，调整各隐层和输出层的权值矩阵Wl和偏移向量bl.

Wl=Wl-ηδl(Hl-1)T

(11)

bl=bl-ηδl,l=2,3,…，L

(12)

Step 6：根据误差阈值ε或迭代次数上限，判断训练过程是否结束.若没有结束，则转至Step 2.

2 EMD-DNN负荷曲线预测模型

2.1 EMD-DNN协作预测模型

基于网络模型训练和测试基本思想，在网络训练阶段需对电力负荷时序数据进行处理，构建相应的训练样本.训练样本以天为单位构建输入输出序列，各天包含96点负荷测量值，测量间隔为15分钟，即：

dij,i=1,2,…，k;j=1,2,…，96

(13)

式(13)中，dij表示第i天第j个时刻点上的负荷值.

若第m天96点负荷时序为d(m)，历史输入时序表示为D(m)，期望负荷序列为Qd(m+h).

D(m)=[d(m-t),…，d(m-1),d(m)]

(14)

Qd(m+h)=[d(m+1),…，d(m+h)]

(15)

式(14)～(15)中，t表示输入时间维度的天数，从时序预测角度出发，该值确定了在电力负荷预测中，负荷时序在模型输入端所占节点的个数，h表示对未来负曲线预测的天数.本文t取值为20，h取值为7，即表示利用过去连续三周的历史负荷序列对未来连续七天的负荷曲线进行预测.在对模型进行训练和测试前，首先利用最大最小归一化方法将原始数据转换到[0,1]范围，归一化公式如下.

x*(x-xmin)/(xmax-xmin)

(16)

式(16)中，xmax为样本数据的最大值，xmin为样本数据的最小值.

在对负荷时序序列进行归一化后，划分训练和测试样本集,其中，EMD-DNN电力负荷预测模型训练过程描述如下.

输入:输入特征向量D(m)，Qd(m+h)

输出:DNN模型集合M

方法：

1) 设定IMF分量个数n=5,t=20,h=7,初始化n+1个DNN模型

2) 利用EMD分别对D(m)和Qd(m+h)进行分解，得到各IMF分量IMFD(m)ii=1,2,…，n，

IMFQd(m+h)i,i=1,2,…，n及残差r(m)，rd(m+h)

3) fori←1 tondo

4) 输入序列集合：IMFD(m)i，输出目标集合：IMFQd(m+h)i

5) 训练第i个DNN模型

6)M←M+DNNi

7) end

8) 训练残差的DNNn+1模型，输入为r(m)，输出为rd(m+h)

9)M←M+DNNn+1

10) 返回M

在利用EMD-DNN电力负荷预测模型预测过程中，对输入的负荷时序进行分解，得到各时序IMF分量和残差分量，最后将各IMF分量和残差分量输入到对应的预测模型中.具体的测试过程描述如下：

输入:输入负荷时序D(m)，训练后的模型集合M

输出:预测负荷序列集合Y

方法：

1) IMF分量个数n=5,t=20,h=7

2) 利用EMD分别对D(m)进行分解，得到各IMF分量IMFD(m)ii=1,2,…，n及残差r(m)

3) fori←1 tondo

4) 第i个分量IMFD(m)i在模型Mi上的预测输出yi

5) end

6)r(m)在模型Mn+1上的输出yn+1

8) 返回Y

根据上述训练和测试流程，基于EMD和DNN的短时电力负荷预测模型流程如图2所示.

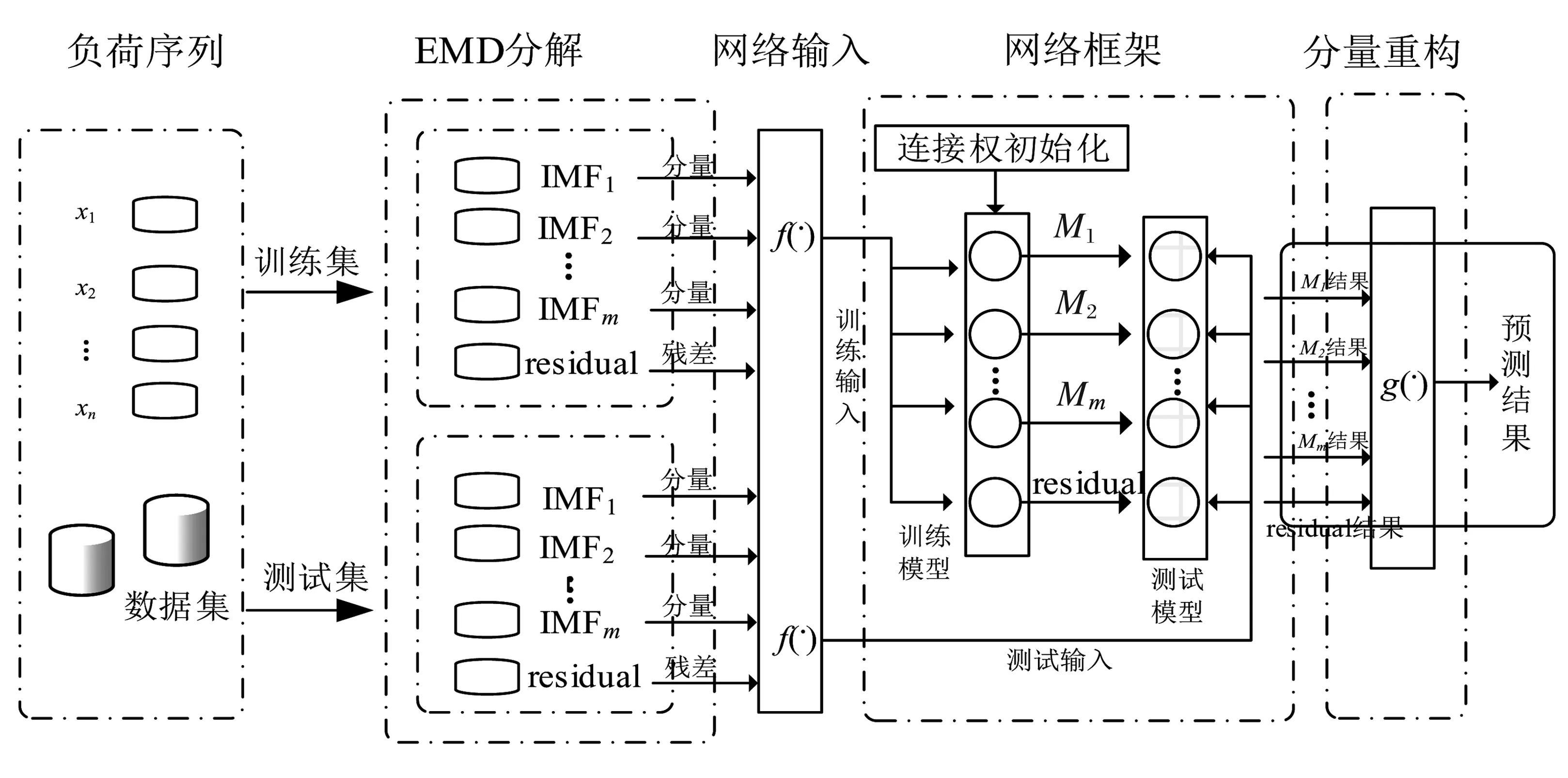
图2 基于EMD-DNN的短时负荷曲线预测模型

2.2 预测模型评价指标

电力负荷曲线预测模型结果的准确性对发电计划的调整有重要影响.因此，为了对模型预测结果进行客观评估，以平均绝对误差(Mean Absolute Error，MAE)、均方根误差(Root Mean Squard Error，RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error，MAPE)作为主要评价指标，各指标的定义如式(17)～(19).

(17)

(18)

(19)

3 实验验证

为了对电力负荷的预测效果进行验证，以某发电单位采集的电力负荷数据为基础，构造训练样本集和测试样本集.其中，电厂负荷数据每隔15分钟记录1次，每日共96个时序数据值.图3为连续七日电力负荷时序数据归一化结果.其归一化序列经EMD算法分解得到5个IMF分量和残差分量.从负荷归一化趋势图中可以看出,电力负荷曲线虽然整体上具有日相似性，但在曲线的细节部分，电力负荷趋势仍具有一定的差异性和波动性.

图3 归一化负荷序列及其EMD分解结果(2018/11/26—2018/12/02)

考虑到数据变化趋势之间的差异性，DNN模型必须具备对不同负荷曲线的学习能力.因此，合理、准确地标定参数，对保证DNN的预测效果至关重要.设定DNN模型各层的节点数及激活函数如表1所示.

表1 DNN模型参数

同时，算法测试的硬件环境为 Intel(R) Core(TM) i5-9300H CPU @2.4 GHz 处理器,16 GB内存，软件环境为Python 3.7，keras 2.3.1.在训练过程中，设定训练次数为600次，损失函数采用均方误差函数(Mean Square Error,MSE)，使用Keras自带的Adam对学习率进行优化，为防止过拟合Dropout层的值设定为0.1.

根据第2.1中EMD-DNN预测模型的训练和测试流程，对2018年11月26日至2018年12月2日连续七日的电力负荷曲线进行预测.其中，训练数据为2017年11月21日至2018年11月25日时间范围内的负荷数据.EMD各分量及其负荷预测结果如图4所示.

图4 EMD分量及其负荷序列预测结果(2018/11/26—2018/12/02)

图5为分别采用DNN和EMD-DNN对连续七日(2018年11月26日至2018年12月2日)电力负荷的预测结果.表2为采用EMD-DNN预测方法与单一的DNN预测方法预测结果的指标对比.根据仿真结果，采用EMD-DNN的节假日电力负荷曲线预测结果的指标值MAE为402.951 8，RMSE为588.945 1，MAPE为0.042 6.采用DNN的节假日电力负荷曲线预测结果的指标值MAE为547.908 8，RMSE为742.747 0，MAPE为0.057 0.可见，在相同网络结构下，采用EMD-DNN算法在提高模型预测精度方面相较于直接采用DNN具有一定优势.

图5 连续七日负荷预测结果对比(2018/11/26—2018/12/02)

表2 电力负荷预测评价指标

4 结论

本文针对短时电力负荷曲线的预测问题，采用了EMD算法对负荷时序进行分解，构建相应的输入输出样本.在此基础上，利用DNN对输入输出样本进行训练，以实现对未来七天负荷曲线的预测.实验结果表明，基于EMD-DNN的预测模型能够对负荷曲线进行预测.同时也值得指出：受节假日、气象等因素的影响，以及模型本身参数设定等问题，负荷曲线的预测精度仍需要进一步提高.因此，在后续的理论研究和工程实践中，将进一步深化电力负荷与各影响因素之间的分析，优化DNN模型参数，进一步增强模型的实际应用价值.