由燕尾模型引出的一类圆锥曲线定值问题

李 波

(重庆市铜梁二中,402560)

一、 问题呈现

(1)求椭圆C的方程;

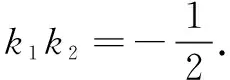
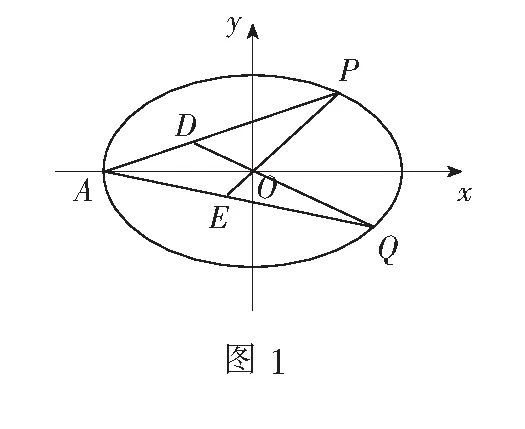
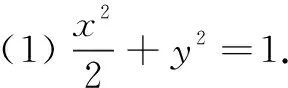
二、 推广及溯源

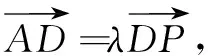
椭圆与圆可经过仿射变换互变,我们发现圆也有类似于性质1的结论,即

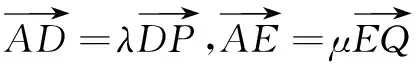
我们可以看出例1实质上是以命题1为背景的,这是平面几何中的“燕尾模型”.

下面给出双曲线和抛物线上与性质1类似的结论,证明留给读者.

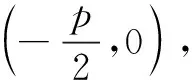
三、变式探究

圆上有如下两个有趣的性质.

命题2设P,Q是圆C:x2+y2=r2(r>0)上的两点,A的坐标为(-r,0),直线AP,AQ的斜率分别为k1,k2,则k1k2=1当且仅当P,Q关于y轴对称.

证明设点P关于x轴的对称点为P′,则AP′的斜率为-k1.若k1k2=1,则kAQkAP′=-1,有AQ⊥AP′.故Q,O,P′三点共线,即点Q,P′关于原点对称.进而点P,Q关于y轴对称.

反之,若点P,Q关于y轴对称,则点Q,P′关于原点对称,可得∆AQP′为直角三角形,且kAQkAP′=-1.所以k1k2=1.

通过仿射变换可以看出,椭圆有与上面两个命题相应的结论.

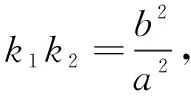
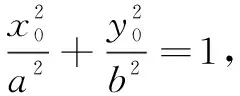
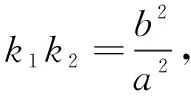
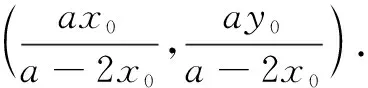
双曲线也有与以上两个性质完全类似的结果,证明留给读者.