核心关联再探究 问题解决添新路——从一道高考题谈起

钱 程

(扬州大学数学科学学院，225002)

高考题是命题专家经过反复推敲、精细打磨而成的,具有良好的教学借鉴与利用价值,同时还引领着高中数学解题的教育方向,具有很高的教学价值.威廉·卡尔文曾说:“智力就是你不知怎么办时动用的东西.但是富有智慧则有更多的涵义,这是一种创造性能力,凭借这种能力你会瞬即想出新主意,各种答案在你的大脑中接踵而至,一些比另一些更好”[1].在数学解题教学中,向学生传达明确的数学解题思想,让学生领悟其中精髓,从而达到培养数学思维,提高解题效率的目的.本文以一道高考题来说明.

一、简析解题思路，情境再现

题目(2018年江苏·数学理13)如图1，在∆ABC中,角A,B,C所对应的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为______.

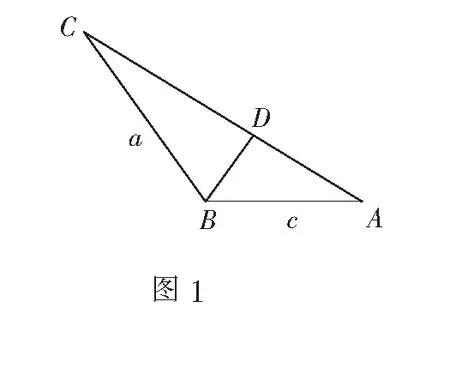
思路要求4a+c的最小值,意味着该式中一定有变量,否则就无最小值一说.a,c都在变化,否则由图1可知,若∆ABC中a,c有一个确定,则∆ABC就是确定的,说明a,c都在变化,则这是一个二元变量求最值的问题.

此解法是学生最易想到的解法,直接采用数形结合方法进行探究,快速且便捷.除了以上的方法,在探究和教学这道题时,是否还有其他方法找到核心关联的思路?

二、探求核心关联，异曲同工

1.解三角形

如图2,利用余弦定理与角平分线第二定理方可找出a,c之间的关系即:

评注在后续的验证中会舍弃a=c,不做赘述,但此方法只有在学生知晓角平分线第二定理的前提下才可实现,在中学阶段具有一定的局限性.

2.利用几何作图

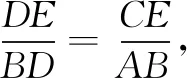
评注采用构造菱形图形的方法,得到∆CDE与∆ADB相似,进而快速得到a，c的核心关联.

评注采用构造等边三角形的方法,得到∆ADB与∆ACG相似,进而快速得到a、c的核心关联.

3.利用解析几何方法

评注以∠ABC的顶为原点，BC边所在直线为x轴,构造平面直角坐标系,表示出A，C，D三点坐标,利用AC的直线方程表示出a，c的核心关联.

三、剑指问题结果,水到渠成

由以上解法都可以得到解题关键式a+c=ac亦或是它的等价式a=c(a-1),那么接着往下思考就会有更多的选择.

解法1最常见的也是学生在解答时最易想到的方法:基本不等式.但是学生在选择基本不等式进行解答时会有2种不同的思路,

解法2 转化为一元函数问题进行解答,由a+c=ac得到则令f(a)=4a且a≠1),有令f′(a)=0,有或故f(a)在和上单调递增,在和上单调递减,极大值为和故最大值为9.

故极值4a+c=9.