同构思想在教学中的应用——以导数问题教学为例

李 安

(江苏省常熟中学，215500)

纵观近年各地高考,导数作为考查热点、难点，频频以指数函数和对数函数混合的形式呈现给考生.这类问题主要考查零点问题、不等式恒成立或有解问题.常用的解决方法有三种:一是指数对数分离后转化为易于求最值的函数;二是利用放缩法将指数函数或者对数函数转化为多项式,然后再作处理;三是直接求导研究函数最值,借助隐形零点消去指数或对数，化简运算.2020年新高考山东卷21题第(2)问的众多解法中,运用“同构”思想将一道复杂的导数题精彩地转化为结构简洁的单调性问题,可谓“四两拨千斤”.这种问题解决的快感,让老师和学生们都开始关注起“同构”这把利剑.在去年4月份的苏州市高三数学二轮复习研讨活动中,笔者以“同构思想在导数问题中的应用”为题开设一节公开课,受到听课教师的一致好评,现将课堂实录及教学反思呈现给大家.

一、课堂实录

1.课前思考

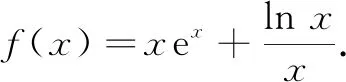
(1)求证:函数f(x)有唯一零点;

(2)若∀x∈(0,+∞),xex-lnx≥1+ax恒成立,求实数a的取值范围.

教师提前一天让学生完成上面的题目,并要求遇到问题后请保留原稿,课前整理学生的解答并投影呈现.

问题1请学生甲来说说解答时遇到的困难是什么?

追问1:是什么导致化简失败?

师生互动:学生甲分析原因,指出需转化的式子是指数对数混合式.

追问2:那些你会转化的式子的结构又如何?

师生互动学生思考,发现能转化的是简单的指数型或对数型式子.学生在教师引导下尝试通过多项式这个桥梁，把指数对数混合式转化到指数型或对数型.教师提出跨阶函数、跳阶函数的概念.我们不妨把指数和多项式混合的函数称为跨阶函数,同样对数和多项式混合的也称为跨阶函数,而既有指数又有对数的称为跳阶函数.目前,我们还没有能力直接去处理跳阶函数,所以需要把跳阶函数转化为低一阶的跨阶函数.

设计意图通过实际遇到的问题,引导学生观察函数结构,激活学生已有的知识储备,为本节课研究同构式找到探究方向.

2.探究归纳

问题2请写出你比较熟悉的跨阶函数,以一次函数和指数函数、对数函数混合为例.

师生互动引导学生写出y=xex和y=xlnx积型的跨阶函数,y=x+ex和y=x+lnx和型的跨阶函数.

追问1:以y=xex和y=xlnx两个积型跨阶函数为例,寻找两者联系,是否能互化?

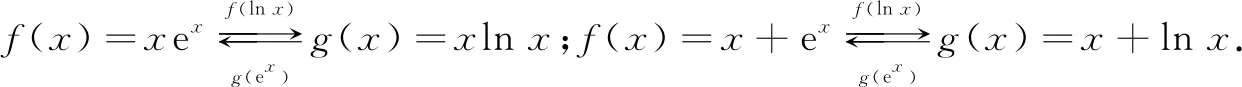
追问2:我们知道和差互为逆运算,你能找到y=ex-(x+1)这个差型跨阶函数的同构型函数吗?

问题3请学生甲回答,课前遇到的隐形零点问题能否通过同构这个思想方法降阶后化简呢?

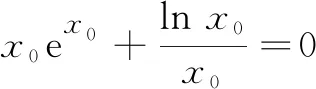
设计意图让学生独立思考、自主探究,回答本课时两个重要问题:同构式到底是什么?同构式可以解决什么问题?

3.小试身手

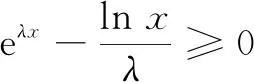
师生互动学生审题后,请学生乙交流思考过程.首先指数对数分放不等式两侧,并使参数在同一侧,原不等式等价于λeλx≥lnx.再利用一次函数作桥梁两边同乘x形成积型跨阶函数,有λxeλx≥xlnx.学生乙选择结构同左构造函数f(x)=xex,将不等式等价于f(λx)≥f(lnx)，最后利用f(x)的单调性完成此题.

学生丙在学生乙的基础上选择结构同右构造函数f(x)=xlnx,将不等式等价于f(eλx)≥f(x).此时,教师引导学生,能否构造和差型跨阶函数.讨论发现,通过两边同取对数将不等式化为λx+ln(λx)≥lnx+ln(lnx),可构造函数f(x)=x+lnx,于是不等式等价于f(λx)≥f(lnx).

例2已知函数f(x)=ex-aln(ax-a)+a,a>0若f(x)>0恒成立,求实数a的取值范围.

师生互动学生独立做题,教师巡视答疑,指导学生探索调整不等式结构.首先参数a与lnx分开,通过真数x-1,联想到若构造的跨阶函数是外层函数,则x-1为内层函数,从而可把不等式等价转化为ex-ln a+x-lna>ln(x-1)+x-1.构造函数g(x)=ex+x,则不等式等价于g(x-lna)>g(ln(x-1)),利用g(x)的单调性完成本题解答.

设计意图让学生初步掌握同构式怎么构造,如何选取函数.同时进一步了解同构思想可以运用于零点问题,也可解答不等式恒成立问题.

例3(2020年高考山东卷21题)已知函数f(x)=aex-1-lnx+lna.

(1)略;

(2)若f(x)≥1,求实数a的取值范围.

师生互动学生独立解答,通过上一环节,学生基本可以顺利构造函数.教师利用多媒体呈现解答.

解不等式f(x)≥1即aex-1-lnx+lna≥1⟺ex+ln a-1+lna-1≥lnx⟺ex+ln a-1+x+lna-1≥x+lnx,所以构造函数g(x)=ex+x,则g(x+lna-1)=ex+ln a-1+x+lna-1,g(lnx)=x+lnx,所以原不等式等价于g(x+lna-1)≥g(lnx)．因为g(x)=ex+x在R上递增,所以不等式等价于x+lna-1≥lnx恒成立,故lna≥(lnx-x+1)max=0,从而a≥1.

设计意图通过走近高考题,让学生进一步深刻理解同构是什么？同构解决什么问题？怎么同构？同时规范学生利用“同构”思想解答问题时的书写.

4.再探课前思考题

师生互动整理课前思考题时发现，有一部分学生解答第(2)小题并未借助第(1)小题中的隐形零点,请学生丁用多媒体展示他的解答：将∀x∈(0,+∞),xex-lnx≥1+ax恒成立整理成∀x∈(0,+∞),ex+ln x-(x+lnx)-1≥(a-1)x恒成立.令t=x+lnx,不等式左侧换元构造g(t)=et-t-1,由已有知识可知g(t)≥0恒成立所以当a≤1时,左侧(a-1)x≤0恒成立,此时不等式恒成立，所以a≤1满足题意，然后引导学生找到a>1时的矛盾点，当a>1时,左侧t=0时，有g(0)=0,用零点的存在性定理可证明t=x+lnx存在唯一正零点x0,此时(a-1)x0>0与不等式恒成立矛盾.综上a≤1.

问题4这个解法并没有把不等式化到左右同构函数,但左侧的函数构造上与本节课的同构思想是否是相通的?

师生互动学生独立思考,学生戊回答两者都是把指数对数跳阶函数降阶变为跨阶函数,化到我们比较熟悉的那些函数,便于化简运算.两者都是通过换元,构造形式更为简单的外层函数和内层函数,是把复合函数像剥洋葱那样一层一层分解开来，教师肯定学生的思考发现,总结本节课同构思想的本质.同构从某种意义上不是表面上构造左右相同结构的函数,借助单调性来解决不等式恒成立问题,方程有解问题那么浅显,同构思想的本质是换元降阶.

设计意图通过再探课前思考题,挖掘提升对同构思想本质的理解.通过本节课的学习,学生能意识到同构式需要构造一个母函数,即外层函数，通常为f(x)=xex，f(x)=x+ex，f(x)=ex-x-1这三个母函数.在这里,跳阶函数需要先变形转化才能同构,如何变形,又能变形成哪些常用形式,未作深究,等学生基本结构比较熟练后再加深研究本节课，旨在让学生看到同构思想的本质.学生只有真正回答了一开始提出的三个问题,才能把同构思想运用得心应手.

二、教学反思

苏步青说过:“学习数学要先知其然,然后知其所以然”.要想真正学通学透“同构”,就必须认真回答好三个问题:同构式到底是什么?同构式能解决什么问题?同构式怎么构造,如何选取函数?本节课的教学,正是围绕着这三个问题的探究解决而展开的.教学过程可概括为两句话:“三问题孜孜以求作探究,四层次步步为营明同构”.

具体这节课的结构与设计如图1所示.为解决上述三个问题,本课选取多个典型题目,分成四个片段“课前思考、探究归纳、小试身手、再探课前思考”展开教学,这四个片段依次可概括为:“探”同构、“出”同构、“用”同构、“扩”同构,步步为营,通过这节课的教学最终让学生达到“明”同构.

在教学中,注意放手让学生进行探究,适时启发,将思维逐步引向深入,直至本质.在“课前思考”教学片段中,首先问“解答时遇到的问题是什么”,再追问“是什么导致你化简失败”,“那些你会转化的式子的结构又如何”.以此三个问题来“探”同构,以教学中学生碰到的真实问题为研究对象,引出解决此类问题的有效方法,并对函数模型进行概括,这是对同构的初探.紧接着在“探究归纳”教学片段中,让学生列举以一次函数和指数函数、对数函数混合的跨阶函数,并归纳成和差积商四种模型,这是从抽象到具体的过程,是“出”同构的过程.通过这两个环节的教学,让学生明白了“同构式到底是什么？”“同构式能解决什么问题?”第三个环节“小试身手”是“用”同构的过程,以三个例题作为同构方法的应用体验,将问题解决的机会均留给学生,对如何变形趋同，如何构造函数？由学生交流讨论,完成问题三“同构式怎么构造,如何选取函数?”同时也使学生对“同构式能解决什么问题”的理解更为深刻,让学生积累了较为有用的数学活动经验.至此,似乎教学任务已完成,但本节课的教学并未止步于此.第四个环节“再探课前思考”将我们进一步引向深入,是“扩”同构的过程,揭示数学的本质.同构从某种意义上说不像我们理解的仅仅是构造左右相同结构的函数,借助单调性来解决不等式恒成立问题和方程有解问题那么浅显,同构思想的本质是换元降阶,做到画龙点睛.

同构思想总结起来为“同在前,构在后;同是难点,构是落点;同是形式,构是内涵;同构是方法,降阶是本质”.