基于双重注意力LSTM 神经网络的可解释海上风电出力预测

苏向敬，周汶鑫，李超杰，米 阳，符 杨，董朝阳

（1. 上海电力大学电气工程学院，上海市 200090；2. 新南威尔士大学电气工程与通信学院，悉尼2052，澳大利亚）

0 引言

近年来，可再生能源发电规模发展迅速，其中风能因其分布广泛、资源丰富和零污染的优点成为目前可再生能源利用的主要形式［1］。相比于陆上风电，中国海上风能资源更为丰富，且靠近负荷中心而具有更好的消纳能力，这使得海上风电逐渐成为中国风电发展的重要方向［2］。然而，海上气象和水文条件复杂多变，风电出力受气象、尾流等因素的影响。同时，海上风电出力集中送出后通常接入岸上配电网，而考虑海上风电场多位于经济发达的沿海地区，其配电网自身负荷较重，受海上风电接入的冲击影响更为显著。因此，高精度且可靠的出力预测能够为海上风电的调度和运行提供必要依据［3-4］，对促进海上风电开发利用意义重大。

风电出力受环境特征影响显著，相比于陆上，海上气象条件演化快、海况复杂，如何提取环境数据与海上风电出力间的深层非线性相关性，成为提高海上风电出力预测精度的关键［5］，这就对出力预测模型捕捉关键信息的能力提出了更高的要求。一般来说，通过充分考虑不同特征间的时空相关性并增强关键信息表达、弱化冗余信息，有助于提升预测模型的性能。例如：文献［6］采用小波变换将风力时间序列分解后通过长短期记忆（long short-term memory，LSTM）网络进行功率预测；文献［7］基于海上风电机组风能转换系统的物理过程设计了输入特征，并通过皮尔森系数和深度学习算法探究特征间的相关性；文献［8］提出将卷积神经网络（CNN）与双向LSTM 网络相结合，从特征空间和时间角度提取数据信息。上述海上风电出力预测方法虽在一定程度上加强了对特征相关性信息的挖掘，但均提取局部特征信息，难以获取全局特征相关性，造成特征关联信息的丢失。同时，上述方法仅关注模型训练前输入特征与目标特征间的固有关联，因此对各时间的输入特征均分配相同的权重。但风电机组出力输入特征与目标特征间的相关程度随时间不断变化［9］，对输入特征时序相关性的挖掘提出了更高要求。

同时，鉴于海上风电接入对岸上受端电网的冲击影响更为显著，在实际工程应用中须增强预测模型和预测结果的可靠性。故在提高出力预测模型精度的同时，获得其预测结果的可解释性有着重要意义［10-11］。可解释性是通过向人类展示模型学习过程、工作机制，从而实现预测过程透明化和模型可理解的能力［12］。然而，现有出力预测模型普遍为“黑箱”，未能实现预测性能与可解释性的兼顾［13］。“黑箱”模型内部结构的复杂性使得其决策过程无法以人类可理解的形式展现，导致模型预测结果在实际应用中可信度偏低。故从模型的实际工程部署角度来说，寻求模型解释是现阶段人工智能模型所面临的重要挑战［12］。可解释性不仅能够通过突出影响预测结果的潜在对抗性扰动提升模型的鲁棒性［14］，同时能够辅助决策者理解模型做出预测结果的依据，实现对变量间潜在因果关系的验证［15-16］。

针对上述不足，本文提出一种基于双重注意力LSTM（dual-stage attention LSTM，DALSTM）网络的可解释海上风电出力预测模型。在LSTM 神经网络的基础上引入特征和时序双重注意力机制，以动态捕捉输入特征与目标特征间的潜在相关性，并增强对输入序列中关键信息的表达。更重要的是，借助双重注意力机制在模型训练过程中的权重动态分配，可实现对输入特征和时序重要信息的评估，进而结合领域知识实现对模型预测结果的解释。最后，基于中国东海大桥海上风电场真实的数据采集与监控（SCADA）数据开展仿真，验证本文所提DALSTM 网络模型对超短期海上风电出力预测的有效性与优越性。

1 DALSTM 网络模型

本文所提DALSTM 网络预测模型以LSTM 神经网络为基础模型，用以捕获风电出力的动态特性和输入序列间的长短期时序依赖关系［17-19］。同时引入输入特征和时序双重注意力机制，其中特征注意力机制用以学习输入特征对目标特征的贡献度，时序注意力机制用以识别历史时刻对当前时刻预测的贡献。

1.1 注意力机制

LSTM 神经网络对所有信息进行无差别压缩，忽略了特征之间的相关性和输入信息的时间差异［20］。注意力机制是一种资源分配机制，可自适应地为输入信息分配注意力权重，以评估不同输入对期望输出的贡献率，并突出重要输入信息的影响［21-22］。在机器翻译［23］、语音识别［24］等领域，注意力机制已取得了显著的应用效果。本文通过引入注意力机制实现对LSTM 神经网络预测性能的改善，同时通过对模型训练过程中注意力权重变化趋势及最终结果的可视化，一定程度上实现模型的可解释性。

1.1.1 特征注意力机制

在所提DALSTM 网络模型中，特征注意力机制被用于LSTM 网络的输入特征提取过程。通过对模型输入特征动态分配注意力权重，挖掘输入特征与目标特征之间的关联关系，将注意力集中于重要特征，减少甚至忽略无关特征。这一过程可有效解决传统相关性分析方法导致的特征关联信息丢失的问题。

特征注意力机制的结构如附录A 图A1 所示，以第t 个时间步为例，含M 个特征的单时间步输入特征向量xt=[ x1，t，x2，t，…，xM，t]。采用单层神经网络计算得到注意力权重向量et［25］：

鉴于特征注意力机制位于模型的浅层，且输入特征数据通常集中在一定数值范围内，本文通过Sigmoid 函数在非线性变换过程中将权重系数映射到（0，1）区间，以提升注意力权重的全面性。

1.1.2 时序注意力机制

时序注意力机制通过对输入序列各历史时刻携带的时序信息分配注意力权重，以区分其对当前时刻预测输出的影响。同时，可自主提取各历史时刻数据间的时序信息，并增强关键时刻的信息表达。

时序注意力机制结构如附录A 图A2 所示，输入为模型迭代至时刻t 的LSTM 网络单元隐藏层状态ht=[h1，t，h2，t，…，hk，t]，其中k 为输入序列时间窗口长度。当前t 时刻对应各历史时刻的时间注意力权重向量lt为［25］：

式中：lt=[l1，t，l2，t，…，lk，t]；Wd为可训练权重矩阵；bd为计算时间注意力权重的偏置向量；ReLU(·)表示激活函数，用以增加特征差异，并使权重分配更为集中。

通过式（5）中的Softmax 函数对各时间注意力权重系数归一化，得到时间注意力权重βt=[ β1，t，β2，t，…，βτ，t，…，βk，t]，其中βτ，t为第τ 个时刻的注意力权重值，与各相应历史时刻的隐藏层状态进行加权，得到综合时序信息状态h＇t。

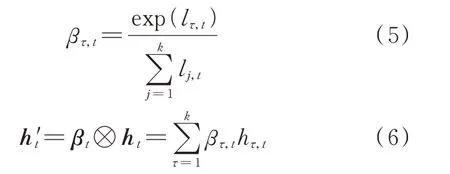
式中：⊗表示矩阵乘积。

1.2 DALSTM 网络模型结构

通过将上述输入特征和时序注意力机制引入LSTM 网络，本文所提DALSTM 网络模型的完整结构如图1 所示，主要包含输入层、特征注意力层、LSTM 网络层、时序注意力层和全连接层。

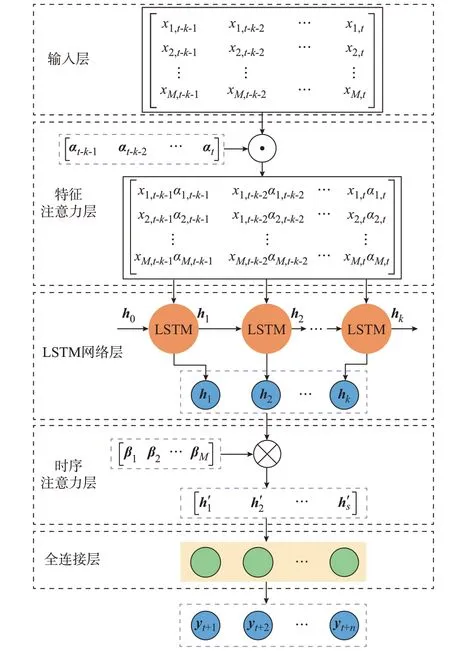
图1 DALSTM 网络模型结构Fig.1 Structure of DALSTM network model

具体流程为：首先，采用特征注意力机制挖掘输入特征间的潜在相关性，具体将风电出力历史序列和相关输入特征序列组成的输入样本X 送至特征注意力层，并通过特征注意力权重的动态分配实现对特征的提取，获得加权输入序列X＇；随后，搭建LSTM 网络层结构，并从加权输入特征序列提取隐藏的时序关联信息，得到各历史时刻的隐藏层状态h；在此基础上，通过时序注意力层挖掘相关特征时间序列各时刻信息{hτ}和当前时刻数据间的相关性，并采用时序注意力机制对其分配时间注意力权重，以增强关键历史时刻信息的表达，获得加权后的综合时序信息状态h＇；最后，将含各历史时刻信息的全局隐藏层状态h＇送入全连接层，输出未来n 步的出力预测yt+n。

2 完整海上风电出力预测流程

在上述所提DALSTM 网络训练模型的基础上，结合数据准备和模型测试环节，可得到本文完整海上风电出力预测流程，如图2 所示。

图2 海上风电出力预测流程图Fig.2 Flow chart of offshore wind power output forecasting

2.1 数据准备

由于恶劣的气象条件，海上风电机组SCADA系统传感器故障或通信网络拥塞问题频发，相比于陆上风电机组面临着更严峻的数据缺失问题［26］，因此需要针对海上风电SCADA 数据设计适合的缺失数据填充方法。完成缺失数据填充后的数据集根据目的可划分为训练集和测试集。对于训练集数据，以风速、风向、环境温度等为代表的气象特征与风电出力有着天然强相关性。同时，考虑海上风电气象特征变化剧烈，本文基于现有气象特征进一步构造统计特征，并结合原始特征形成输入特征集用于模型训练。在此基础上，对输入特征集和测试集数据做归一化处理，分别获得新的训练集和测试集。

2.2 模型训练

本文采用反向传播算法进行预测模型训练［27］。以实现式（7）、式（8）中多步损失函数最小的训练目标［28］，并采用Adam 优化器对模型中各层系数进行迭代更新［29］，得到最终的DALSTM 海上风电出力预测模型。

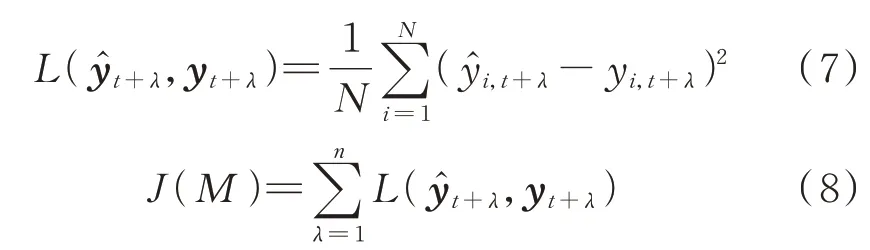
式中：N 为训练样本数；ŷt+λ为模型t 时刻输出的第λ步出力预测值；yt+λ为对应的出力真实值；n 为多步预测步长；ŷi，t+λ和yi，t+λ分别为模型t 时刻输出的第i个样本第λ 步出力预测值和对应的真实值。式（7）为单步损失函数，式（8）为多步损失函数，定义为各步损失函数之和。

2.3 模型评价

为量化评价所提DALTSM 网络预测模型的性能，本文采用均方根误差（RMSE）指标ERMSE和平均绝对误差（MAE）指标EMAE作为误差评价指标。上述指标数值越小，表示预测精度越高。同时采用确定系数R2评估模型有效性，其值越大，表示预测模型对数据的拟合效果越好。具体计算公式如下：

2.4 模型可解释性

预测模型可解释性的关键在于捕获单个变量的动态以及多变量间的相互作用［24］。传统LSTM 网络模型在计算隐藏层状态时将所有输入变量数据混合，无法对单个变量的时序动态进行区分。为此，本文通过引入双重注意力机制，在模型训练过程中对各输入特征和各历史时刻的注意力权重进行动态分配，以获得其对预测结果的贡献度。同时，通过热力图可视化不同特征和时间注意力权重的变化趋势及最终结果、监测预测过程中的注意力行为，从而一定程度上实现了预测模型的可解释性。

3 算例分析验证

为验证所提DALSTM 海上风电出力预测模型的可行性与优越性，本文基于东海大桥海上风电场真实SCADA 数据开展案例仿真和分析。

3.1 仿真案例设置

东海大桥海上风电场位于上海东海大桥东侧距海岸线8～13 km 的海域。项目一期共安装了34 台单机容量为3 MW 的离岸型风机，风电场经四回35 kV 海底电缆接入岸上110 kV 升压变电站，并入上海市电网。风电场平均水深为10 m，风机设计高度为90 m，代表年主风向为E-SSE，风速在3.5～25.0 m/s 出现的频率占96%，年平均风速为8.4 m/s。风电场海域潮汐为非正规半日浅海潮，设计表层潮流流速为3.15 m/s。受季风、副热带高压等因素影响，风电场出力具有明显季节特性，整体表现为春季和夏季相对较低，而秋季和冬季相对较高［30］。

东海大桥海上风电SCADA 系统数据采集周期为15 min，记录了气象、空气动力学及机组主要部件的运行参数等共15 个特征，具体如附录A 表A1 所示。这些SCADA 特征数据共同构成了本文所提模型的训练集和测试集。同时，通过动态挖掘各特征间的时空相关性，并观察其注意力权重分配变化，实现对模型的解释。

仿真案例设置方面，为验证所提DALSTM 网络模型的预测精度，本文基于2019 年10 月至2020 年12 月的海上风电SCADA 数据，对比多种现有风电出力预测模型并进行单步与多步出力预测仿真。在此基础上，通过可视化注意力权重的变化趋势，对模型预测结果的合理性进行解释。

仿真参数设置方面，模型原始输入特征维度为15，目标特征为预测时刻的风电机组出力。本文设定输入序列的时间窗口长度k 为20，即利用第1 至20 时刻的输入特征序列对第21+n 时刻的出力进行建模。LSTM 网络的隐藏层维度为32，层数为1；模型学习率设为0.001，训练批次设为64，迭代次数为1 000，并选择Adam 优化器。

3.2 数据预处理

本文提取风电机组SCADA 系统采集的正常运行数据用于模型训练。根据机组运行手册，可编程逻辑控制器（PLC）状态代码为7 时表示机组处于稳定发电的正常运行状态，故仅保留PLC 状态代码为7 的数据。在此基础上，对缺失数据进行填充处理并添加统计特征数据，以提升预测效果。

3.2.1 缺失数据填充

SCADA 数据缺失问题主要包含由传感器故障引起的部分特征数据缺失和由网络拥塞引起的部分时段全部特征数据缺失2 种类型。针对部分特征数据缺失，考虑风电机组各子系统特征间具有强时空相关性，本文采用文献［31］提出的多变量时间序列生成对抗网络（MTS-GAN）进行填充。针对部分时段全部特征数据缺失，本文基于临近风电机组间的空间相关性对目标风电机组缺失值进行填充［32］。填充后的数据集，取其中80%作为模型训练集，其余20%作为模型测试集。

3.2.2 添加数据统计特征

为进一步提升模型预测精度，基于SCADA 数据集现有气象特征构造其统计特征，包含-1point风速、近1 风速对近3 趋势、近风速3 个mean、近风速3 个max、近环境温度3 个max、平均变桨力矩及平均变桨角度等共12 个特征。其中：-1point、-2point、-3point 分别表示前1、2、3 个点的数值；近1 风速对近3 趋势表示前1 个时间步的风速值与前3 个时间步风速值之比，用于捕捉风速变化的趋势；近风速3 个mean 表示前3 个时间步风速的均值；近风速3 个max 表示前3 个时间步中风速的最大值；近环境温度3 个max 表示前3 个时间步中环境温度的最大值。结合所构造的统计特征与训练集原有特征共同构成新的27 维输入特征矩阵，提供给预测模型进行训练。

3.2.3 数据归一化

因所选数据集由不同特征数据组成，不同特征量纲不同且数值差异较大。为避免对模型训练效果产生不利影响，通过式（12）对输入数据归一化［33］。

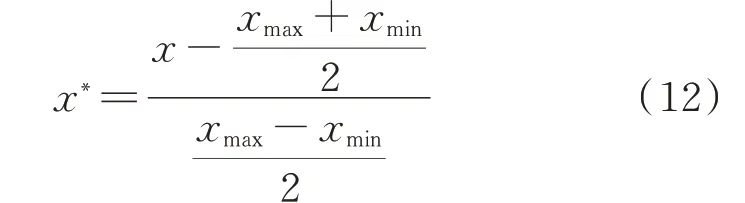
式中：x 和x∗分别为归一化前、后的值；xmax和xmin分别为原数据的最大值和最小值。

所有特征中，风向反映了风速在某特定方向上的投影系数，依据其物理意义，采用正弦函数对风向进行归一化处理。同时，变桨角度作为角度特征，也采用正弦函数进行归一化计算。

3.3 模型预测性能

本节主要通过仿真对比验证所提DALSTM 网络的预测性能：先添加统计特征的预测效果并进行分析；再通过与现有预测模型的对比，分别验证所提DALSTM 网络对单步和多步出力预测的效果。

3.3.1 添加统计特征

为评估添加统计特征对模型预测的影响，分别基于原始特征数据集和加入统计特征的数据集建模。附录A 图A3 和表1 分别展示了二者的预测曲线和预测误差。由图A3 和表1 可知，基于添加统计特征的新特征集，模型出力预测结果的RMSE、MAE 指标明显降低，同时R2显著提高，表明了合理添加统计特征可有效提升模型预测精度和数据拟合效果。

表1 基于不同特征数据集的预测误差对比Table 1 Comparision of forecasting errors based on different feature datasets

3.3.2 单步出力预测

为验证所提DALSTM 网络对单步出力预测的精度，基于相同数据集和仿真参数设置，分别与现有海上风电出力预测模型LSTM、CNN-LSTM、特征注意力LSTM（FALSTM）和时序注意力LSTM（TALSTM）进行仿真对比。各模型预测结果如表2 所示，附录A 图A4 展示了其对应出力预测曲线。

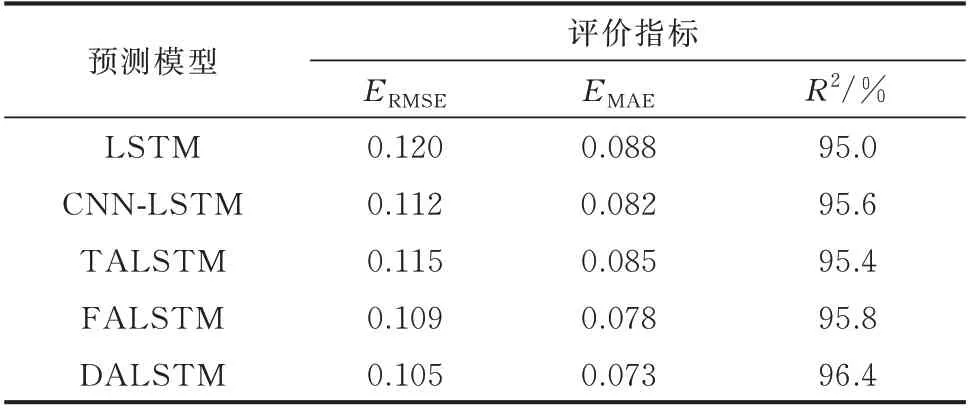
表2 不同模型单步出力预测结果对比Table 2 Comparision of one-step output forecasting results of different models

上述结果表明，CNN-LSTM 模型和引入注意力机制后的TALSTM、FALSTM 模型相比，传统LSTM 模型预测精度更高，且数据拟合效果更好。具体来说，CNN-LSTM 模型通过CNN 进行输入特征提取，进而结合LSTM 进行出力预测，其预测精度的提高验证了特征提取过程的必要性。而引入时序注意力机制的TALSTM 模型，其RMSE 和MAE相比于LSTM 分别下降了1.71%和3.41%，R2值也略高于LSTM，但其模型性能相比于CNN-LSTM略低。这是由于TALSTM 模型通过为各历史时刻分配注意力权重，能够避免信息丢失并增强关键时刻信息的表达，相比LSTM 获得了预测模型准确性的提升；但因其仅关注时间相关性，没有对特征相关性信息进行有效挖掘，应用于海上风电出力预测时精度相比CNN-LSTM 仍显不足。同时，引入特征注意力机制的FALSTM 模型，其RMSE 相比于LSTM 和CNN-LSTM 分别下降了4.27% 和2.68%，MAE 分别下降了11.36%和4.88%，且R2值升高。这表明特征注意力机制相比于CNN 具有更优越的输入特征提取能力，FALSTM 模型通过为各输入特征分配注意力权重，可有效提取输入特征与目标特征间的关联关系，并提高预测精度。

本文提出的DALSTM 模型在单步预测情况下，精度相比于CNN-LSTM 有明显提升，证明了其对输入特征空间和时序相关性的深度挖掘能力，在海上风电出力预测中具有显著的优势。同时，其预测效果也均优于上述引入单一注意力机制的FALSTM 和TALSTM 模型，反映出引入双重注意力机制的综合优势。由附录A 图A4 可知，双重注意力机制的引入使得模型的预测曲线更接近原始数据曲线，表明注意力机制通过学习数据间依存关系并提取关键信息，对提高出力预测精度具有重要帮助。

3.3.3 多步出力预测

为验证所提DALSTM 模型的多步预测能力，基于相同数据集及仿真参数设置，分别采用LSTM、CNN-LSTM、FALSTM、TALSTM 和本文所提DALSTM 模型开展仿真。具体分别针对风电机组出力进行4 步（1 h）、8 步（2 h）、12 步（3 h）和16 步（4 h）的超短期预测。表3 给出了其预测效果对比，同时附录A 图A5 展示了对应多步出力预测曲线。

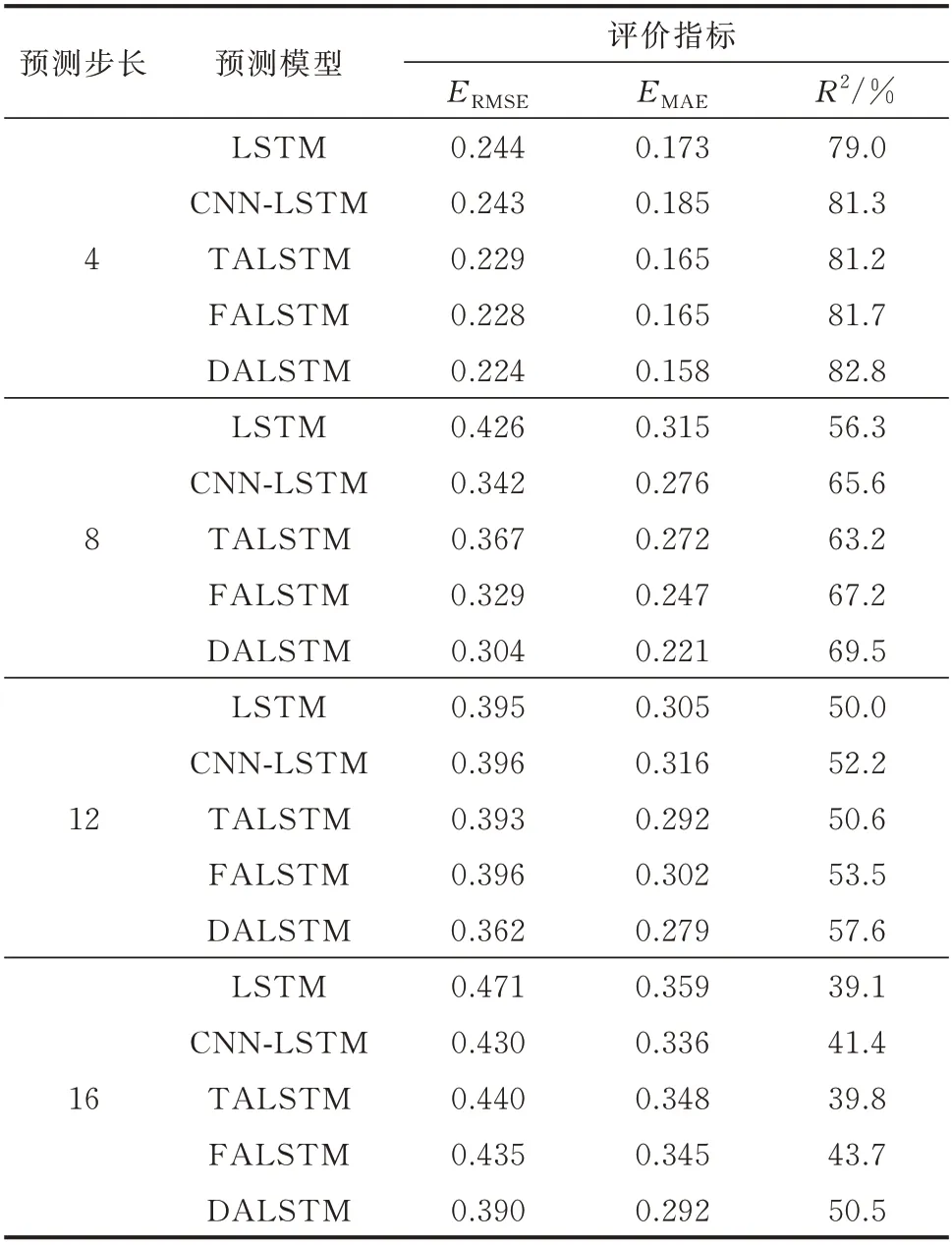
表3 不同模型多步出力预测结果对比Table 3 Comparision of multi-step output forecasting results with different models

由表3 可见，基于不同出力预测模型的RMSE和MSE 值均随预测步长的增加而升高，即预测误差增加。同时，R2随预测步长的增加而降低，即数据拟合效果下降。这是由于随着预测步长的增加，待预测的风电出力值与输入历史时间序列数据间的依赖性减弱，并导致预测模型精度下降。

对比表3 和附录A 图A5 可知，随着预测步长增加，FALSTM 模型相比于CNN-LSTM 模型始终具有更好的预测性能，表明了特征注意力机制在多步预测中仍具有较好的特征提取能力；而所提DALSTM 模型在各预测步长下均具有最高的预测精度和模型拟合度。同时观察图A5 可知，相比其他预测模型，DALSTM 模型具有更高的模型稳定性，即可以更好地拟合出力数据的变化趋势，且随着预测步长的增加其相对优势愈发明显。具体表现为：在4 步和8 步出力预测中，DALSTM 的RMSE值相比对应步长下RMSE 值最小的FALSTM 模型分别降低了1.75%和7.60%，R2值分别提升了1.1%和2.3%；在16 步出力预测中，DALSTM 的RMSE值相比FALSTM 模型降低了10.35%，R2值提升了6.8%。故所提DALSTM 模型在海上风电多步出力预测中优势更加明显。

3.4 模型的可解释性

所提DALSTM 模型在模型训练和测试过程中通过注意力权重的动态分配，能够实现对输入特征空间和时序重要性的评估。对于模型训练过程，通过可视化不同迭代次数单样本的注意力权重，能够对各特征和时刻的重要性变化趋势进行定量分析，进而借助领域知识对其进行评估，可以实现模型预测过程的可解释性。图3 和附录A 图A6 分别展示了DALSTM 模型在训练过程中的特征和时间重要性。同时在模型测试过程中，对不同月份连续样本的特征注意力权重值进行可视化和定量分析，并结合水文气象知识验证结果解释的合理性。图4 展示了DALSTM 模型在测试过程中的特征注意力权重连续变化。

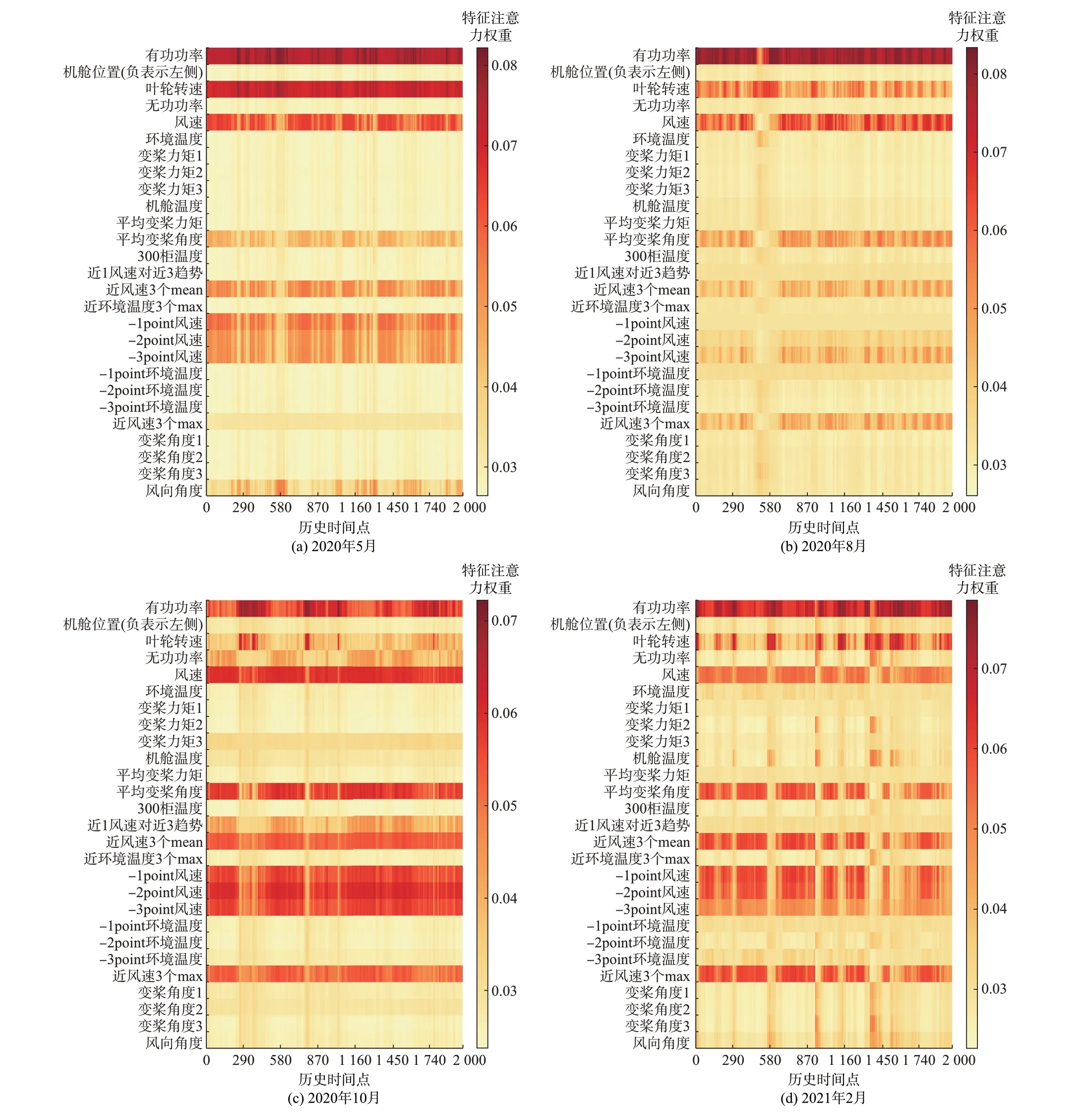
图4 不同月份连续样本注意力权重Fig.4 Attention weights of continuous samples in different months

3.4.1 模型训练中的特征权重解释

模型在迭代训练过程中对不同输入特征动态分配注意力权重，并在训练结束时确定特征重要性排名。重要性高的特征对海上风电出力预测有着更大贡献度，并会对预测结果产生更大影响。图3 分别给出了模型在第10 次、50 次和97 次（收敛）迭代时的特征注意力权重热力图，其中横轴为样本时间跨度，间隔为15 min，其中时间点20 距离预测时刻最近。纵轴为输入特征，色块深浅表示特征注意力权重大小。图3 展示了特征注意力权重在模型迭代过程中的动态变化，表明特征注意力机制可挖掘SCADA 数据集输入特征与目标特征间的空间关联。

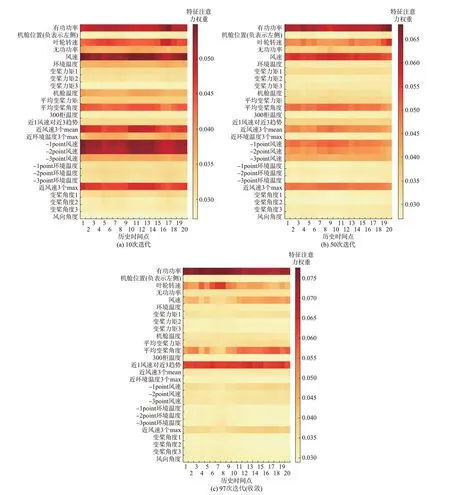
图3 模型训练中的特征注意力权重变化趋势Fig.3 Changing trend of feature attention weights in model training

具体来说，在模型迭代收敛过程中，输入特征“风电出力”的注意力权重逐渐上升至0.073，对风电出力预测过程的贡献度最高，即对预测结果的影响最大。对于人工添加的统计特征：“近1 风速对近3趋势”的注意力权重在模型迭代至收敛时达到0.068，且随迭代次数增加对模型预测结果的相对贡献度也表现出明显的提升。由图3 可知，模型在第10 次、50 次迭代时，该特征注意力权重在整体特征集中排序靠后，而当模型迭代至收敛时，其权重排在第2 位。这表明“近1 风速对近3 趋势”有助于实现对海上风速变化趋势的捕捉，在模型训练迭代过程中表现出对预测结果的影响程度不断提高。同时，“叶轮转速”及“平均变桨角度”的注意力权重均在0.056 左右，“风速”的注意力权重在迭代过程中存在波动并收敛到0.048，其他风速相关统计特征注意力权重值在0.042 左右，剩余特征注意力权重则较低，对出力预测结果的影响较小。另外，对比不同迭代次数的热力图可知，“出力历史值”“风速及相关统计特征”“叶轮转速”“平均变桨角度”等特征在迭代过程中始终占有较高的权重，表明这些特征对出力预测结果的影响更大，与风电出力的相关性也更大。

实际中，“出力历史值”与预测值相关度最高，直接影响着预测结果；“风速”为风电出力的关键影响因素，“叶轮转速”直接受风速影响，故两者及其统计特征均表现出对出力预测过程较高的贡献度。故领域知识与上述仿真结果吻合，从特征重要性角度证明了本文风电出力预测模型的合理性。

3.4.2 模型训练中的时间权重解释

在模型迭代训练过程中，时间注意力机制关注各历史时刻数据对风电出力预测过程的贡献度，附录A 图A6 展示了模型在第10 次、50 次、97 次（收敛）迭代时的样本时间注意力权重热力图。由图A6可知，模型迭代前期时间注意权重几乎是随时间线性增加，且距离预测时刻越近权重值越高。随着迭代次数的增加，携带关键信息的时间注意力权重逐渐上升。当迭代收敛时，模型主要关注距预测时刻更近的时间步，即这些时间步蕴含的信息对出力预测结果影响更大。

值得注意的是，本文设定样本输入序列时间窗口长度为20，即单样本包含20 个时间步。在此5 h时段内风电出力尚未表现出明显的周期性，故距离预测时刻越近的时间步携带的信息对预测结果影响越大。上述领域知识与附录A 图A6 中结果一致，从时间重要性角度验证了本文预测模型的合理性。

3.4.3 模型解释能力对比

在上述特征和时间权重解释的基础上，通过对比所提的DALSTM 和单注意力FALSTM、TALSTM 模型来验证其模型的解释能力。具体来说，FALSTM 模型包含特征注意力层、LSTM 层及全连接层，与DALSTM 模型具有相同的特征注意力分配过程，故二者具有相同的特征权重解释能力。但FALSTM 模型仅通过LSTM 层进行时序信息提取，不具备时间重要性的解释能力。TALSTM模型则包含LSTM 层、时序注意力层及全连接层，仅能实现时间重要性解释。为进一步探究引入双重注意力机制的DALSTM 模型的综合优势，本文对模型迭代收敛时DALSTM 与TALSTM 注意力权重热力图进行了对比。如附录A 图A7 所示，距预测时刻越近，TALSTM 时间注意力权重越高，而DALSTM 除对距离预测时刻近的时间步分配较高权重外，还表现出对该样本窗口内其他时间步的关注。这是由于特征注意力层对特征关联关系的动态挖掘，加强了关键特征在各历史时刻的表达，在实现深度特征提取的同时影响着不同时间步对预测结果的贡献。

3.4.4 模型测试中的连续样本权重解释

海上风电出力易受到气象因素的影响而表现出相比于陆上更明显的季节特性［34］。除模型训练外，为同时说明注意力机制对模型测试过程的解释能力，基于四季中的不同月份进行仿真对比。通过对测试集中连续样本进行特征注意力权重提取与可视化，观察不同季节条件下各特征对出力预测结果的贡献度，并结合水文气象知识验证合理性。图4 为2020 年5 月、8 月、10 月和2021 年2 月2 000 个连续测试样本点的特征注意力权重热力图。

由图4 可见，2020 年5 月“风向”特征的注意力权重较高，即风向对预测结果贡献度更高。这是由于东海位于东亚季风区，5 月为季风转换期，海上风向变化显著，对模型预测的影响增加。2020 年8 月对出力预测结果影响最突出的特征为“历史时刻出力”，同时相比于其他月份“风速”特征影响有所降低。这是因为夏季多为偏南风，风向平稳且风力相对较弱，海上温度也相对稳定，各气象特征影响差异不大。2020 年10 月“风速”及其相关统计特征注意力权重明显升高，这是由于该月份东海受热带气旋和冷空气影响，常出现偏北大风天气，故“风速”对预测结果影响更为显著。2021 年2 月与2020 年10 月各特征注意力权重基本一致，而“环境温度”特征注意力权重略有升高。因为冬季盛行强劲偏北风，且环境温度波动相对明显，表现为对出力预测结果的贡献度提升。

4 结语

本文提出了一种基于DALSTM 的可解释海上风电出力预测模型。在LSTM 神经网络的基础上引入特征和时序双重注意力机制，通过注意力权重的动态分配，同时对输入特征间的潜在关联和历史时刻蕴含的有效信息进行挖掘，从而提升超短期海上风电出力预测的准确性和可解释能力。

通过上述真实案例仿真对比分析表明：

1）所提DALSTM 海上风电出力预测模型在进行单步出力预测时具有优越的预测精度；

2）所提DALSTM 模型在进行多步出力预测时仍可保持较高的预测性能，具有更高的稳定性，且随预测步长的增加其相对优势愈发明显；

3）本文所提出力预测模型具有一定程度的可解释能力，经验证能得到合理的模型解释结果，对实际工程具有更加可靠的参考和应用价值。

值得注意的是，海上风电出力预测受气象、海况等多重不确定性因素的影响，往往具有较高随机性，对并网运行带来挑战。本文从预测模型可解释性的角度开展研究，以提升预测结果的可靠性，后续可以综合考虑各种不确定性因素的统计特征，开展海上风电出力的概率预测研究。同时，鉴于海上风电数据的完整性与准确性偏差，后续可对数据清洗、补全等预处理开展研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。