例析整体思想法求解不等式问题的策略*

江苏省新沂市第一中学 (221400) 苗庆硕

整体思想是建立在整体与局部这种对立统一辩证关系上的一种数学思想方法，它要求以广阔的视野来看待所研究的数学对象，在统揽全局的思想指导下，整体地考察和处理问题，再抓住个性特征谋求解题突破，以达到简化和优化解题的目的.经常有目的地引导学生进行这样的训练，能进一步培养学生思维的广泛性、敏捷性和深刻性，在教学和学习中应该受到重视.如在解答某些不等式的问题中，若将题设或结论视为整体，通过对整体结构的调节或转化，可以收到简化运算、降低思维难度、缩短推证过程之功效.本文通过分析不等式问题的典型题例的解法，从如何运用整体思想处理数学问题的角度，谈一些常用做法和使用经验，供同仁参考.

一、整体表示

视问题的多个结论为整体，根据结构特征，合理变形，直接求出欲求的答案.

例1 设函数f(x)=ax2+bx且满足不等式1≤f(-1)≤2，2≤f(1)≤4，求f(-2)的取值范围.

评注：通过将待求的f(-2)整体的用f(-1)和f(1)表示出来，再运用不等式相加解决问题.本题如果先分别求出a和b的范围，再代入f(-2)=4a-2b求范围，就可能造成范围扩大的错误.

二、整体换元

在一些轮换式的不等式中，通过对相关式子整体换元后，可找到解题突破口.

解析：从待证的不等式可以看到，左边的三个式子是轮换式，可采用整体换元处理.

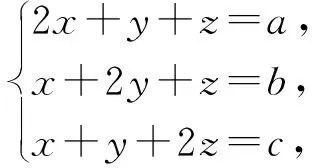
评注：在证明问题时，抓住了分母是轮换式的特点，可将分母视为一个整体进行换元处理，通过整体变形，显露了问题的内含，为用基本不等式解决问题指明了方向.

三、整体变形

把某一相关的知识块看作一个整体，进行整体变形，寻找各知识块之间内在联系.

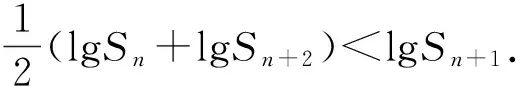
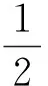
评注：解决关于Sn的问题一般方法是用前n项和公式，并对q=1与q≠1来讨论解决，而本解法中将Sn，Sn+1，Sn+2视为整体，进行变形，避免了分类讨论，使问题获得了简解.

四、整体配凑

在证明分式不等式时，抓住分母的特点进行巧妙配凑也是解题技巧之一.

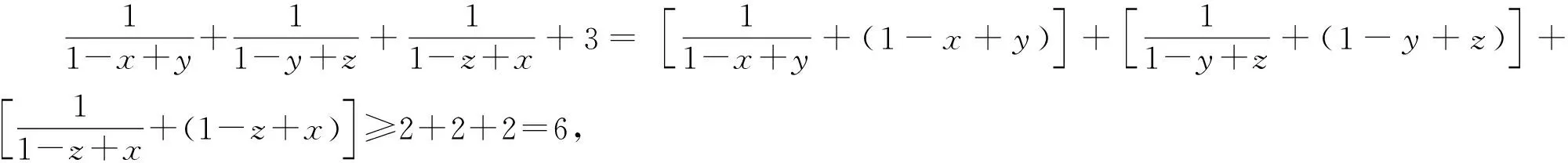
评注：用整体的观念分析1-x+y、1-y+z、1-z+x之间的关系，就能找到他们其中隐含的东西，从而发现了利用基本不等式解题的契机.

五、整体对偶

通过整体地设一个与已知式对偶的式子参与运算和化简也可给我们带来惊喜.

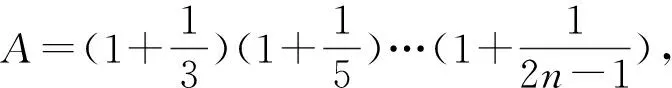
评注：题目中左边出现的是一个整体的分式连乘式，要证明到右边必须进行约分，只有再出现一个与之相乘可以消去左边大部分分式的连乘式才能达到目的，于是对偶的式子就好找了.

六、整体求解

将所求的不等式看作一个整体求解，就可以避免分开求解或分类讨论的情况.

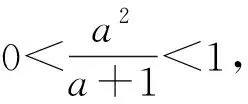
七、整体构造

在证明不等式时，也可以通过整体地构造函数或方程等方法以帮助解题.

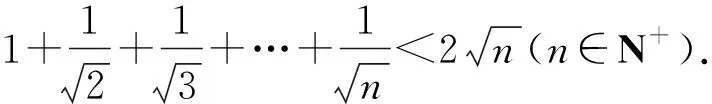
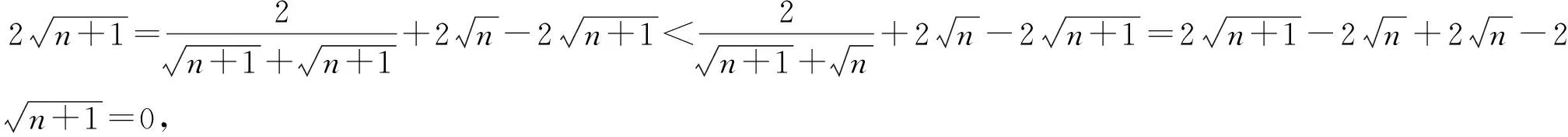
评注：构造法证明不等式也是一个重要方法，而抓住题设进行整体地构造体现了对题意的完全把握和深刻领会，需要有丰富的有经验和较强的能力做支撑.

八、整体构形

通过挖掘所给条件中的几何事实，构造相关的几何图形，利用几何性质帮助解题.

例8 已知m为实数，x>0,y>0，x+y<π,求证：m(m-1)sin(x+y)+m(sinx-siny)+siny>0.

解析：由条件知，存在一个z>0，使得x+y+z=π，于是可构造△ABC，使其外接圆直径为1，三内角为x,y,z，且x,y,z的对边分别为a,b,c，由正弦定理知，待证的不等式即为m(m-1)c+m(a-b)+b>0，即cm2+(a-b-c)m+b>0；因c>0且△=(a-b-c)2-4bc=a2+b2+c2-2ab-2ac-2bc=(a2-ab-ac)+(b2-bc-ba)+(c2-ca-cb)=a(a-b-c)+b(b-c-a)+c(c-a-b)<0，故cm2+(a-b-c)m+b>0恒成立，即原不等式成立.

评注：在分析所给条件中，敏锐地洞察到含有x+y+z=π的隐含条件，为整体构造三角形将不等式转化为三角形三边之间的关系问题求解创造了机会.

九、整体思考

在统揽全局的思想指导下，整体的思考问题，再抓住个性特征去解题.

例9 设a,b，A,B均为已知实数，且对任何实数x，不等式Acos2x+Bsin2x+acosx+bsinx≤1成立，求证：a2+b2≤2，A2+B2≤1.

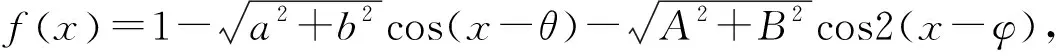
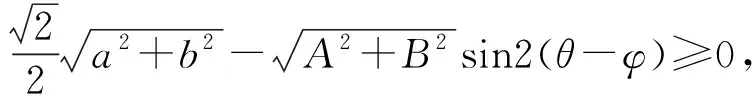
评注：由于题中的主要条件就是一个恒不等式，充分运用这个恒不等式是解题关键，通过整体地设函数，整体地化简合并，然后再整体地运用特殊值变形，使问题获得圆满的解答.