时空轨迹相似性度量方法探讨

郭博雷 田晗 汤玲 杜志强

（1.中国电子科技集团公司第二十七研究所 河南郑州 450047；2.南京北斗创新应用科技研究院有限公司 江苏南京 211500；3.武汉大学测绘遥感信息工程国家重点实验室 湖北武汉 430072）

作为一个整体概念，时空不仅是现实物体存在的维度，也是人类认知和认识世界的模式［1］。具有时间和空间属性的数据或信息出现在日常生产、生活和经济文化活动的各个领域。时空轨迹，即记录运动物体位置随时间变化的数据，是最典型的时空数据类型。近年来，随着各种传感器和定位芯片的大量安装，数据不断积累，数据内容不断丰富，它所包含的信息和知识反映了运动物体的不同运动规律和行为模式，具有相当大的挖掘价值。其中，轨迹相似性是轨迹之间最基本的模式。如何综合考虑轨迹形状和位置不确定性等因素，衡量轨迹和轨迹子段之间的相似性，是许多轨迹数据挖掘和分析应用的要解决的问题。

轨迹相似性分析和相似模式计算是时空数据挖掘的重要内容，是时空数据诸多应用的基础，如异常的轨迹聚类、热点和频繁模式挖掘等相关领域一直保持着较高的研究兴趣［2］。时空建模、时空分析、时空模式挖掘等相关领域的研究一直占据着相当大的比重，尤其是基于轨迹数据分析、挖掘和计算的研究，往往基于新的底层模型扩展新场景。空间数据新应用的新时空轨迹建模和相似性分析再次成为该领域学者关注的焦点。

时空轨迹相似性分析属于计算机科学和地理信息科学的交叉领域，其关键技术包括通用时空数据模型、时空轨迹数据模型、轨迹相似性度量方法、轨迹子段匹配与相似模式挖掘等。结合本文研究内容，下面对时空数据模型、时空轨迹模型及轨迹相似性度量与计算等方面的研究现状作分别介绍。

1 时空数据模型

时空动态变化过程是空间信息在时间域的扩展和完善，传统的空间对象就是时空对象在某一时刻的空间瞬态［3］。时空数据着重于时空过程中的时序关系和时空因果联系，使设计者、开发者和用户能够更好地实现时空对象时间和空间信息的动态表达与建模。时空轨迹的表达与建模更加依赖于通用时空数据模型的设计。时空数据建模所面临的主要难点如图1所示［4］。

图1 时空数据建模所面临的主要难点

在此领域还有多位学者引入了多样化的建模方法，提出了一系列各有侧重的模型成果，如图2所示［5］。

图2 时空数据模型

但这些模型大多只是在上层设计概念模型，没有触及数据底层的组织方式，所以，大多是属于数据与应用之间的中间层级模型，不具备通用性，且对时空因果、时空关联等模式支撑不足，无法在更广泛的问题场景中发挥作用。所以，业界也出现了一些从数据生产和转换层面着手的模型设计，典型代表就是英国陆地测量部的MasterMap项目。如今，大多数GIS 都是基于图层要素模型系统来组织和管理空间数据的。基于OGC 标准下的单元素模型，形成一套结合空间对象和平铺地图的混合数据结构。底层空间数据库也主要基于关系模型。

2 轨迹数据模型

随着各类位置传感器在移动实体的广泛安装，移动对象的轨迹数据成为数据量最大的时空数据类型，最常见的为记录车辆、船只、飞行器、野生动物等移动物体的轨迹数据。许多研究部门和企业都公开了大规模的轨迹数据集，以支撑更加开放、多元的科学研究，例如，滴滴公司的“盖亚”计划公开了数个城市的滴滴快车轨迹数据，数据量达到了数百GB。相应地，面向新的数据现状和应用场景，针对轨迹数据建模的研究也层出不穷，取得了许多新的进展。轨迹模型的研究可以追溯到20世纪70年代，人们为了描述飓风的移动轨迹，反映飓风异动情况和态势，以进行后续的分析和预测，设计了最初的轨迹数据模型［6］，后续也发展了很多轨迹数据模型，如图3所示。

图3 轨迹数据模型类别

在轨迹不确定性建模方面，一种多粒度模型值得特别注意，它使用棱锥状结构来描述一个移动的物体在两个位置采样点之间可能的路径区域，用首尾相接的Bead 形成的连续的珠串表示整条轨迹［7］。其中使用的Bead模型来源于时间地理框架，因形态特征也被称为Prism模型，其数学基础在多个文献中得到了进一步的阐述，包括时空路径和时空棱锥等时间地理学的基本要素。时空Bead 模型对轨迹数据离散采样和插值所带来的位置不确定性进行了建模，但时空三维空间中融合了空间和时间特征的立体Bead 不便于处理和计算。一个经典的简化方法是将Bead 模型投影到空间二维平面上（见图4），成为一个以采样点为焦点的椭圆，再进行后续的分析和计算。很多文献已经基于Bead投影椭圆进行了可达性计算、位置分布预测等研究工作［8］。

图4 B ead 模型在空间平面上的椭圆投影

其他考虑空间位置不确定性的轨迹模型还包括缓冲区模型、圆筒模型、立方网格模型等，大多采用将采样点或采样点间的插值线向外按不同的几何模型扩展一定的距离，作为移动对象可能的位置范围［8］。

3 时空轨迹相似性度量方法分类

3.1 时空轨迹

轨迹数据库T={T1，T2，T3，…，Tf}，包含一系列的原始轨迹，f表示轨迹库中轨迹的条数，其中，每一条轨迹Tj(1≤j≤f) 都是由GPS 等设备记录的位置点{p1，p2，p3，…，pn}的集合，pi表示的轨迹点通常使用经度、纬度、时间戳表示，即(pi·x，pi·y，pi·t)，i表示点在轨迹中的位置。查询序列也是一条轨迹，本文用Q={q1，q2，q3，…，qm}表示，其中，m表示查询序列中元素的个数。

3.2 时空轨迹相似性度量方法分类

由于时空轨迹相似性度量主要依赖于轨迹之间距离的定义，轨迹之间的距离使用轨迹之间的匹配程度来表示，不同的轨迹匹配度量方法对轨迹之间的匹配程度有着不同的解释［9］。

本文将时空轨迹相似性度量方法分为两类：基于轨迹点的相似性度量方法和基于轨迹段的相似性度量方法，如图5所示。由于轨迹主要是以轨迹点的方式进行存储，当对轨迹进行相似性度量时，最直观的方式就是利用两条轨迹中对应轨迹点之间的距离来度量轨迹之间的相似性［10］。基于轨迹点的相似度测量方法有很多种，每种方法都有自己独特的相似度定义和应用场景。例如，一些测量方法认为两条轨迹只需要部分相似，它们是相似的；有些测量方法认为两条轨迹整体上是相似的，它们是相似的。因此，本文将基于轨迹点的相似度测量方法分为两类：全局匹配度量法和局部匹配度量法，具体分类如图5所示。

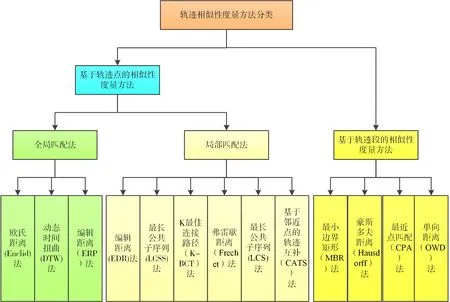
图5 轨迹相似性度量方法分类

4 结语

时空轨迹的相似性分析与计算是众多轨迹模式挖掘应用的重要手段，而轨迹的相似性度量是相似分析等上游应用的重要基础。对不同数据条件和应用场景的轨迹相似性度量进行研究，具有重要的理论和实用价值，并可以有效促进空间数据分析与挖掘方法多样化发展。