绿色金融助推低碳经济转型的影响机制与实证检验*

郭希宇

（中国人民银行曲阜市支行，山东 曲阜 273100）

一、引言

根据世界银行公开数据，近60年来中国二氧化碳排放量总体呈上升趋势，从1960年的1.17公吨/人增加至2018年的7.41公吨/人。我国经济建设取得巨大成就的同时也给生态环境造成较大压力。进入新时期，我国更加重视生态文明建设，经济发展兼顾“优环境”与“稳增长”的双重目标。2021年11月13日，习近平总书记在亚太经合组织第二十八次领导人非正式会议上再次强调，“要坚持人与自然和谐共生，积极应对气候变化，促进绿色低碳转型，努力构建地球生命共同体。中国将力争2030年前实现碳达峰、2060年前实现碳中和。”

从现实出发，如何精准测度及评价绿色金融与低碳经济间的客观现实规律，建设绿色金融进而驱动地区低碳经济转型，以及协调好地区之间绿色金融和低碳经济的空间关联已成为实现绿色金融与低碳经济良性互动、协同发展，最终实现我国低碳转型所面临的重要理论与现实问题。以往研究仅考虑到绿色金融对低碳经济的单向关系，未考虑经济效应的空间溢出规律。基于以上研究背景，本文将绿色金融与低碳经济之间的交互影响与空间溢出效应纳入考虑，并尝试解决以下经济问题：一是系统分析绿色金融与低碳经济的双向影响，克服内生性问题导致的估计偏误；二是同时考察绿色金融与低碳经济间的跨地区空间溢出效应，而后进行经验检验与分析；三是识别绿色金融影响低碳经济的条件性特征和阶段性特征。相较于既往研究，本文的实证结论更具普通性。

二、文献综述、理论机制与研究假设

在研究方向及视角方面，已有文献多集中讨论金融发展对二氧化碳排放的影响，较少从绿色金融视角探讨其对低碳经济转型的作用，以及低碳经济对绿色金融的反向影响（严成樑等，2016）。然而，忽略低碳对绿色金融的反向影响会使实证模型出现严重的内生性问题，进而导致估计结果出现偏误。也有文献从绿色信贷着手，或者将其作为绿色金融的衡量指标，建立计量模型分析绿色信贷政策的环境效应（苏冬蔚等，2018；王馨等，2021）。

从研究方法上看，大部分研究主要通过构造理论或实证模型，对绿色金融与低碳经济的关系进行定量考察。在实证研究设计方面，存在以下问题：第一，在指标设定上，已有研究文献鲜少测算我国分地区绿色金融指数，亦缺乏对我国低碳经济转型的相应测度。第二，在模型构造方面，已有研究多是建立传统面板数据模型，估计本地区绿色金融与低碳经济二者的经济联系，忽视了绿色金融和低碳经济可能的空间溢出效应（王遥等，2019；赵军等，2020）。第三，已有文献多是从全国层面研究中国绿色金融与低碳经济的关系，没有考虑国内不同地区之间的异质性，实际上不同区域、不同省份间的绿色金融指数存在较大差异。第四，现有研究成果大多默认了两者间的“一成不变”的经济关联，进而构建线性回归模型并以此进行参数估计，没有考虑绿色金融影响我国低碳经济转型的条件性特征与阶段性特征。

基于现有研究成果，本文认为绿色金融与低碳经济之间存在交互影响。绿色金融影响低碳经济的主要路径有四个：一是为低碳产业提供资金支持。低碳产业发展、绿色项目建设需要长期充足的资金投入，稳定的资金来源是低碳经济发展的核心问题，而绿色金融政策能够通过丰富的金融工具满足低碳产业资金需求，进而促进低碳经济转型。二是引导企业绿色化转型。银行业等金融机构通过对企业经营领域、生产形式的筛选，将金融政策向低碳型企业倾斜，向市场释放绿色发展信号。同时绿色金融能够优化资本配置，引导资金从“两高一剩”产业流向低碳产业，进而激励更多企业开发环保生产新技术，逐步实现生产低碳化。三是绿色信息披露与绿色监管要求企业低碳运营。绿色金融政策在为低碳产业提供融资服务时会要求相应企业及时披露其低碳发展信息，这会约束企业的碳排放行为，促使其逐渐实现碳减排。银行和证券机构可以对企业资金流向进行追踪检测，在一定程度上规范企业经营行为，监督企业将融得资金进行低碳生产。四是分散低碳技术发展风险。金融本身具有风险分散的功能，可以分散和化解高新产业发展自身的风险，绿色金融为低碳生产技术的探索与创新提供资金基础，其中绿色信贷、绿色保险以及碳金融等政策可以有效地为企业分散低碳技术发展所产生的相应风险。

低碳经济对绿色金融的影响机制主要表现在两个方面：一是低碳经济发展能够促进完善绿色金融发展机制。经济结构转型升级往往会引导、促进金融结构不断优化，低碳经济会对绿色金融提出新发展要求，促进传统金融业不断向绿色金融转变。一个国家或地区的社会经济越发达，其对金融服务的需求则愈大。而在不同经济基础下，金融将会有不同的发展方向和模式，即经济发展方向的变化会引起金融业的适应性调整，国民经济在低碳转型过程中将引导金融业向绿色化转变。武志（2010）认为，产业结构调整和技术进步等方面带来的经济增长能够显著提升金融业发展的内在质量，未来工作重点应放在经济发展质量与效益方面，而非通过无限制地扩张金融规模来刺激经济增长。二是丰富绿色金融工具，提升贷款工具的精准度与运行效率。以“双碳”发展背景下的碳减排支持工具为例，其作为绿色金融专项政策工具，要求“先贷后借”，在进行流动性投放时具备较高精准度；另一方面其要求实体端必须满足监管部门所规定的信息披露、投放方向以及第三方机构核查等条件。该政策工具的落地将会吸引更多的社会资金参与到环保节能生产、清洁能源开发中来，助力绿色金融发展。三是低碳经济转型发展对绿色金融提出了更高的建设要求与监管标准。2016年8月31日，经国务院批准，中国人民银行等七部委联合印发了《关于构建绿色金融体系的指导意见》（以下简称《意见》）。《意见》强调了构建绿色金融体系的重要意义，并明确指出从发展绿色信贷、绿色投资，设立绿色发展基金，发展绿色保险、完善环境权益交易市场，开展绿色金融国际合作等角度落实绿色金融建设，同时明确指出要完善金融、环保、财政等政策和法律法规的配套支持，并且通过建立适当的激励与约束机制解决项目环境的外部性问题。

地理学第一定律指出，任何事物均与其他事物相关，相近事物关联更为紧密。综合以上文献述评与机制分析，并结合地理学相关定律，本研究提出以下研究假设：

H1：绿色金融与低碳经济相互作用，存在交互效应。

H2：绿色金融对我国低碳经济转型的影响存在空间溢出效应。

这种地理空间位置上的经济联系使得本地区低碳经济的发展不仅受到本地绿色金融指数的影响，并且在一定程度上受到其他地区绿色金融建设的外部冲击。

三、我国低碳TFP与绿色金融指数测度

数据包络分析（Data Envelopment Analysis，DEA）由Charnes等提出，是评价决策单元（DMU）多投入多产出相对有效性的分析方法。学术界普遍采用DEA技术测度全要素生产率，本研究遵循这一计算规则。但无论是基于不变规模收益假定的CCR模型还是基于可变规模收益假定的BCC模型，此类径向模型在进行DEA测度时会遗漏松弛变量信息，难以克服径向和角度的问题。为应对这种缺陷，Tone（2001）提出SBM-DEA模型，这是一种非径向、非角度的非期望产出模型，能较好地解决上述问题。基于此，构造评价我国低碳全要素生产率的非期望产出SBM-DEA模型如下：

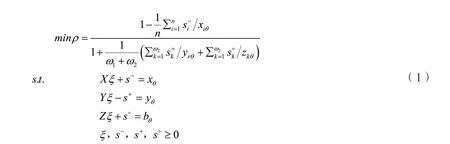
其中：n表示DMU投入要素种类数量，ω1为期望产出的种类数量，ω2为非期望产出的种类数量，xiθ、ykθ和zkθ分别代表投入、期望产出以及非期望产出的向量，s-、s+和s。分别是投入、期望产出和非期望产出的松弛变量，ξ表示常数向量。目标函数ρ关于s-、s+和s。单调递减，并且ρ∈(0,1]。对于特定被评价单元而言，目标函数效率值ρ愈大，DMU的效率值愈高；当且仅当ρ=1，即s-=0、s+=0、s。=0时，DMU处在效率前沿上，即完全有效；若ρ＜1，则意味着生产单元存在效率损失，可以通过调整优化要素投入、期望产出和非期望产出量以改善效率。

Malmquist-Luenberger（ML）指数是测算生产效率的主流方法，但该指数不具备传递性，在计算跨期方向性距离函数时，线性规划存在无解的可能。Oh（2010）将ML指数与全局生产技术相结合，使所有被评价的决策单元均包含在全局参考集内，构建了Global Malmquist-Luenberger（GML）生产率指数。GML指数在研究低碳全要素生产效率时能够进行跨期比较，克服了传统ML指数存在的非传递性问题以及线性规划中无可行解的缺陷。本文借鉴Qin（2017）的研究思路，用考虑了非期望产出SBM方向性距离函数的 Global Malmquist-Luenberger指数测算低碳全要素生产率，以此衡量低碳经济转型。本研究构造低碳经济GML指数如下：

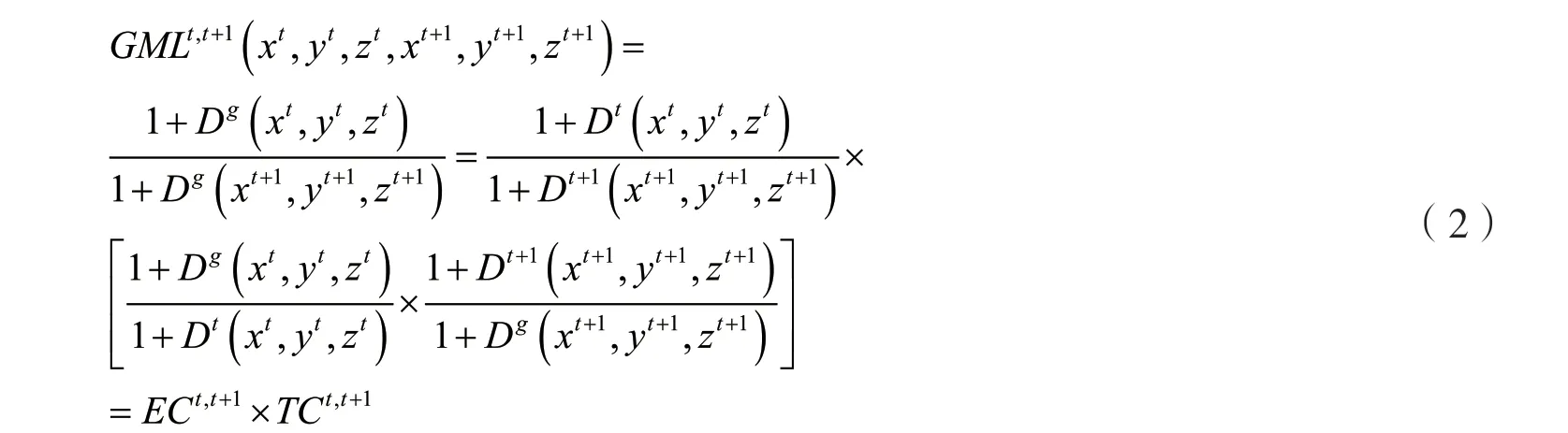
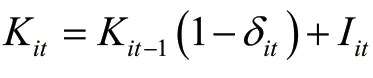
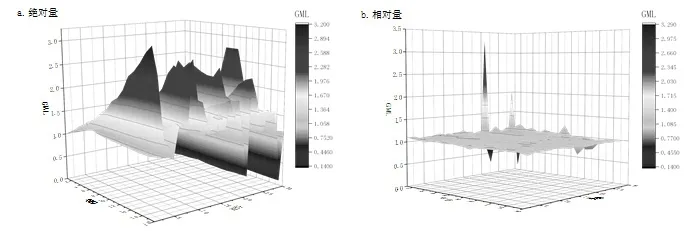
图1 2001—2018年样本省市低碳全要素生产率分布三维曲面图

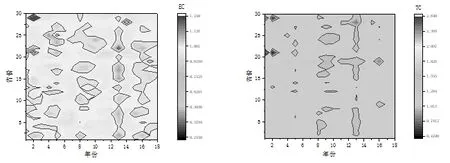
图2 2001—2018年样本省市低碳技术效率变化指数和低碳技术进步指数分布等高线图

从图1可以看出，2001—2018年我国各省市低碳全要素生产率累积值总体分布在0—3的区间内，随时间呈现递升趋势，但不同省市间存在明显异质性。以相对量测度的低碳TFP描述了各省级行政区低碳全要素生产率的跨时期动态变迁，在考察年度内，观测值集中分布在1.0上下，低碳全要素生产率的历年变动较为平稳。图2显示了低碳技术效率变化的整体情况，各地区技术效率总体差异不大，均未突破1.25的峰值。但在2005、2013和2016年有大范围的技术效率跃升，并处在高值状态。对于低碳技术进步，在全国范围内绝大多数观测值稳定在1.0以上，在2008及2013年有小幅下降，但总体而言低碳技术进步表现出小幅稳步提高态势。

既往研究多以绿色信贷表征绿色金融发展水平，难以全面体现绿色金融内涵，本文在已有研究基础上，从绿色信贷、绿色投资、绿色风投和政府支持四个角度出发，综合构建各地区绿色金融指数。所使用数据主要来源于《中国统计年鉴》和各省统计年鉴。其中绿色风投数据来自清科集团（Zero2IPO）的私募通数据库（PEDATA），首先依据发生年份对风险投资事件进行整理，然后依据被投资企业的注册地，将新能源、新材料以及环保三行业的风险投资额与各个省份相匹配，得到2001-2018年的绿色风投数据。最后，采用熵值法测算省际绿色金融指数，指标体系如表1所示。

表1 绿色金融指标体系

总的来看，在考察期内东部沿海省份的绿色金融发展进程整体领先于中西部地区。北京、天津、广东和上海等地的绿色金融指数明显高于其他省份，处在国内领先位置。山东、江苏和浙江等沿海经济大省绿色金融发展紧随其后。此外，重庆、四川、湖北、陕西等地随时间发展出现协同演进趋势，该区域内各省市绿色金融建设处在彼此接近的水平；而以新疆、青海、云南、甘肃等为代表的西部省份处在绿色金融发展的初步阶段。

四、实证研究设计

（一）模型构建

1.权重矩阵设定

相较于传统计量模型，空间计量模型将经济规律中普遍存在的空间依赖性纳入考虑，即观测值在空间上缺乏独立性——本地区的样本观测值受到其他地区观测值的密切影响。并且根据地理学第一定律，相近地区有更为紧密的联系，空间相关的模式和程度依赖于地区之间的绝对与相对位置。首先，借助GeoDa和ArcGIS软件，建立简单的0-1空间权重矩阵，两地区相邻为1，不相邻则为0，如式（3）所示。

考虑到21世纪以来互联网技术尤其是信息通讯、AI、大数据以及云计算等的大发展，地区间的联系比以往更紧密、更高效，同时考虑到国内完善的交通基础设施环境，省份之间的关联在一定程度上缓解了地理距离上的障碍，经济距离意义上的空间关联表现得愈加明显。参考张学良（2012）的研究，以人均地区增加值差异为矩阵基础元素，构建描述经济发展水平差异的空间权重矩阵，如式（4）所示，其中pGDP表示人均地区生产总值。

基于邻接关系或地理距离构建的空间权重矩阵，忽略了空间观测单元之间互相作用的经济和社会因素，因而在研究经济金融领域问题时常受到质疑。但是，地理距离依然是研究地区经济空间关联不容忽视的影响因素，因此，在经济距离权重矩阵的基础上考虑地理距离因素，构建经济地理嵌套矩阵，全面考察经济与地理因素，如式（5）。其中，distanceij表示地区i和地区j之间以经纬度坐标计算的地理距离。

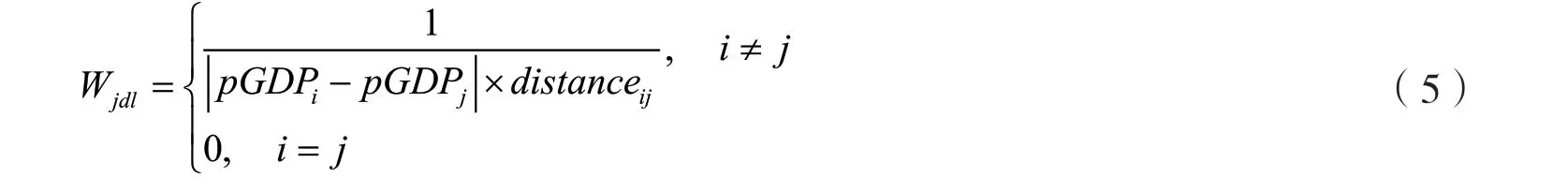
Shao等（2020）认为，经济发达的地区对经济落后的地区影响相对更大，因此应当赋予更大的空间权重，这种差异可用两地人均GDP的比值度量。基于此，兼顾地理距离因素，构建非对称经济地理嵌套矩阵，如式（6）所示。

2.基准模型选择

实证模型具体形式的选择与设定对参数估计结果的准确性有至关重要的影响。在进行相应检验前，适用何种空间计量模型来探索绿色金融与低碳经济二者间的经济规律并不确定，而相异类型的空间计量模型假定了不同的空间传导机制，其蕴含的经济意义也有所差别。如式（7）所示，首先考察一个广义嵌套空间（GNS）模型，其中LCE表示低碳经济转型指数，GF表示绿色金融指数，W指待构造的空间权重矩阵，X为一系列控制变量，α为常数项，β和ρ是待估参数，μ和ε指随机扰动项。

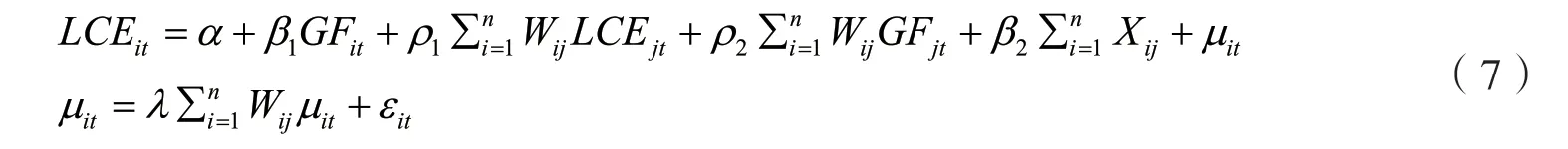
当空间误差项中的λ为0时，GNS模型转化为SDM模型，即式（8）。该方程考察了经济变量之间的交互作用，即本地区的低碳经济指数不仅受本市绿色金融发展的影响，还受到其他地区低碳经济和绿色金融发展的影响。

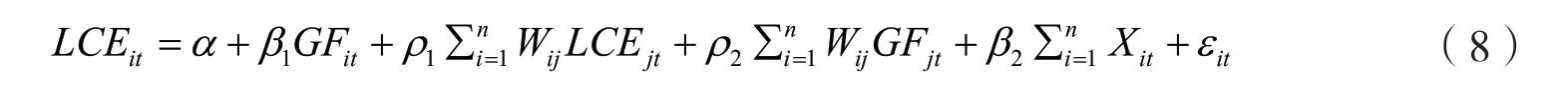
当SDM模型考察的空间交互作用不存在，即ρ2=0时，地区间只存在单向的空间相关性，SDM模型转化为SAR模型。如式（9），其假设低碳经济会通过空间相互作用对其他地区的低碳经济产生影响（Anselin等，2008）。

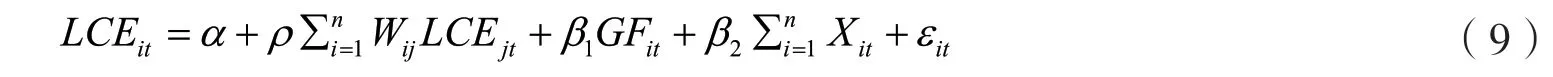
对于SDM模型而言，当因变量回归系数和空间滞后项系数的乘积与空间交互项系数之和为0时，SDM就转化为SEM模型，如式（10）。SEM模型假定绿色金融空间溢出的产生是随机冲击所导致的，其空间效应主要通过误差项传导。

然后对模型设定形式进行相应检验，依次对式（7）施以LM检验、LR检验以及Wald检验，以识别模型的具体形式。结果如表2所示，在4种权重矩阵下，LMlag检验和LMerror检验的结果总体具备较高显著性水平，这表明SEM模型在解释经济问题时优于SAR模型。此外，进一步考察LR检验与Wald检验，结果表明两种检验均显著拒绝原假设，这意味着仅采用SEM模型和SAR模型分析绿色金融的空间溢出效应可能导致估计偏误。因而，选择SDM模型作为数据样本的基准回归模型。

表2 空间计量模型设定检验

最后为了确定回归模型应当使用随机效应还是固定效应，进行豪斯曼检验，结果如表3所示。可以看出，0-1空间邻接矩阵和非对称经济地理矩阵均不拒绝原假设，表明应建立随机效应模型进行分析。而经济地理嵌套矩阵和经济距离权重矩阵皆显著拒绝了应建立随机效应模型的原假设，即应当选择固定效应模型。进一步分析发现，时点固定效应总体R2明显高于个体固定效应和双固定效应下的可决系数，因此择以时点固定效应模型进行后续研究。

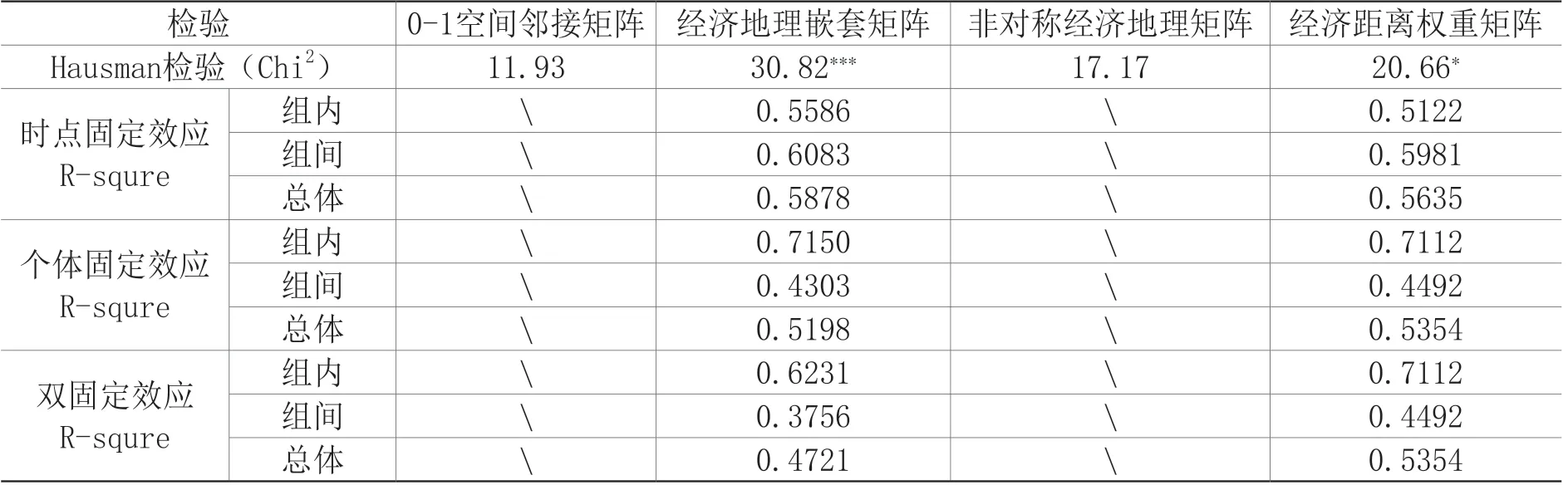
表3 固定效应与随机效应选择

3.空间联立方程模型的建立

综合上述分析，考虑到绿色金融与低碳经济各自的空间溢出效应、空间交互作用以及绿色金融经济与低碳经济可能存在的双向内生关系，建立如下空间联立方程模型。其中，式（11）为绿色金融方程，式（12）为低碳经济方程。式中，μi、ξi和v、ε分别代表地区个体效应和随机扰动因素。

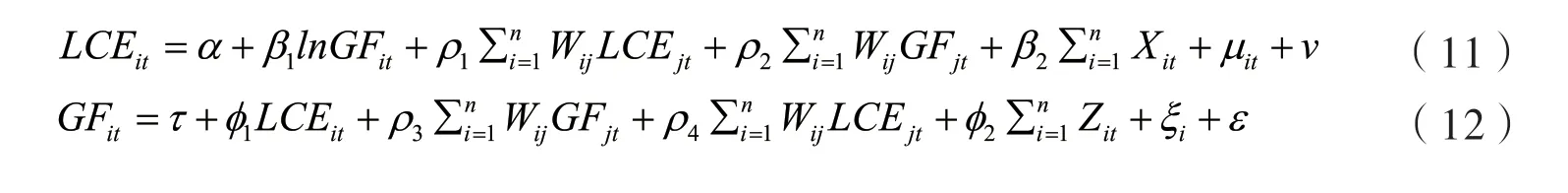
（二）数据来源与描述性统计

本研究所使用数据主要来自中国碳核算数据库（CEADs）、Wind数据库、《中国统计年鉴》、《中国保险年鉴》、各省统计年鉴以及中国人民银行官网等。绿色金融和低碳经济指数的定义与计算在文章第三部分已作说明。在控制变量方面，能源强度（EI）用各省市能源消费总量与地区生产总值的比值测度，实际GDP的基年为2000年，单位为亿元。外商直接投资（FDI）计算方法为：采用年均汇率将FDI折算成人民币，后求出其占地区名义GDP的百分比。工业化水平（INDL）指各省市工业增加值与地区生产总值的比值。城镇化水平（Urban）用各省市城镇人口与地区总人口的比值表示。经济发展水平（lnEDL）以各省人均GDP度量，以2000年为基期，用各省GDP平减指数对各省GDP进行平减。此外，为缓解可能的异方差问题，对所有非比值型和非指数型变量取自然对数。数据的描述性统计如表4所示。

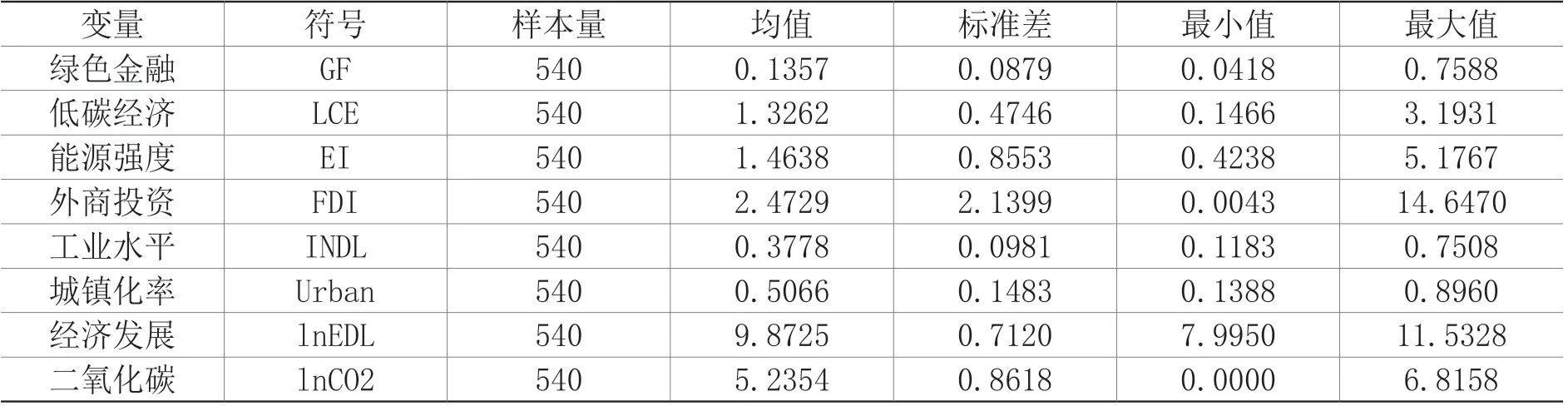
表4 变量的描述性统计

（三）估计方法

对于空间面板联立方程模型，Kelejian和Prucha （2004）提出广义空间三阶段最小二乘（GS3SLS）估计策略，而Baltagi与Ying（2015）则给出了针对空间联立方程的误差成分三阶段最小二乘（EC3SLS）估计方法。其中，GS3SLS方法不仅考虑了内生变量潜在的空间相关性，同时也对各方程随机干扰项的相关性进行了处置。因此本文参考Kelejian和Prucha的研究思路，运用广义空间三阶段最小二乘法（GS3SLS）对式（11）-（12）进行估计。在低碳经济方程中，外生变量选择为能源强度（EI）、工业化水平（INDL）和外商直接投资（FDI）。在绿色金融方程中，外生变量确定为城镇化水平（Urban）和经济发展水平（lnEDL）。

五、实证结果及分析

（一）低碳经济方程的估计结果

根据表5的估计结果可知，绿色金融指数的估计系数为正并且全部在1%的显著性水平下显著，意味着绿色金融发展显著促进了我国低碳经济转型。以表5中非对称经济地理嵌套矩阵的估计结果为例，控制其他变量不变，绿色金融指数每提升1单位，低碳全要素生产率平均提高约4.08个单位，可以看出区域内绿色金融发展对绿色TFP的提升起到了强烈且有效的助推作用。绿色金融可以通过差异化的信贷政策，运用利率手段限制“高污染、高耗能”企业的实施规模，借助市场机制倒逼企业转型升级。与此同时，绿色金融支持环保产业发展，为其融资提供优惠和便利，鼓励低碳企业发展壮大。此外，绿色金融政策可以促进绿色生产技术进步，进而产生碳减排效应，为地区低碳经济转型提供强有力的引擎。

绿色金融空间滞后项的估计系数为正且均在1%的显著性水平显著，这表明其他地区的绿色金融对本省的低碳经济转型产生了促进作用。同样以表5中非对称经济地理矩阵的估计结果为例，能够看出在控制其他变量不变的条件下，邻近地区的绿色金融每提高1个单位，本地区低碳经济指数平均提升2.64个单位。可以看出绿色金融进步不仅能够促进本省低碳经济发展，而且显著助推了相邻省份的低碳经济转型。低碳经济空间滞后项的估计系数为负且在1%的显著性水平下显著，这表明低碳经济存在显著的负向空间溢出效应，相邻地区低碳经济的发展在一定程度上对本地区的低碳经济进程产生了挤出效应。

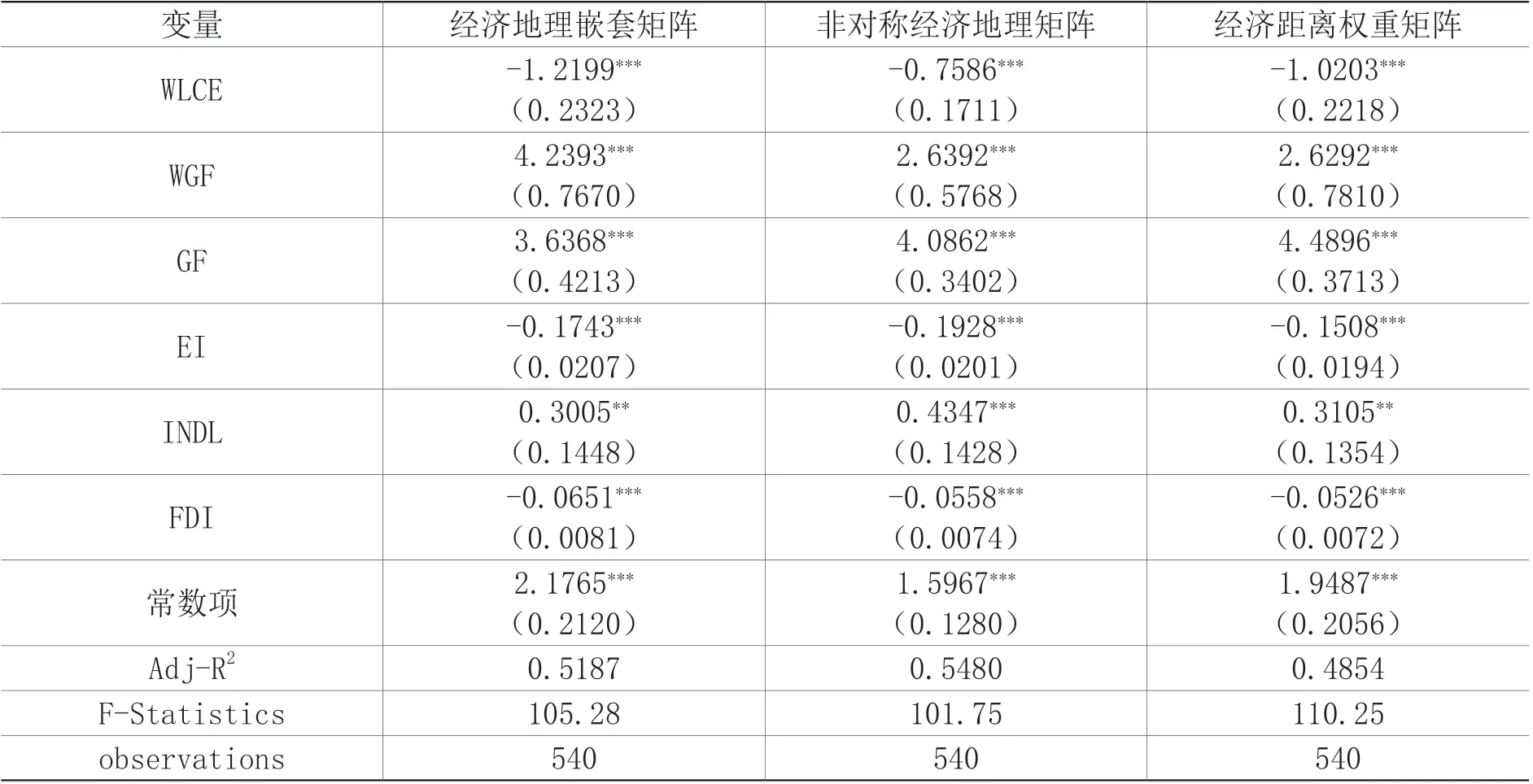
表5 低碳经济方程估计结果

（二）绿色金融方程的估计结果

从表6可知，在3种不同的空间权重矩阵下，本地区低碳经济对绿色金融而言皆起到显著促进作用，并且估计结果较为接近。这表明低碳经济发展有效带动了本区域绿色金融进步。具体而言，以非对称经济地理矩阵为例，在控制其他变量不变的条件下，低碳经济指数每提升1个单位，绿色金融指数平均提升约0.07个单位。低碳经济的确促进绿色金融发展，低碳经济对于绿色产业的需求、对能源与节能技术的需求，将会吸引更多的资金投向绿色发展，进而推动金融的绿色发展。

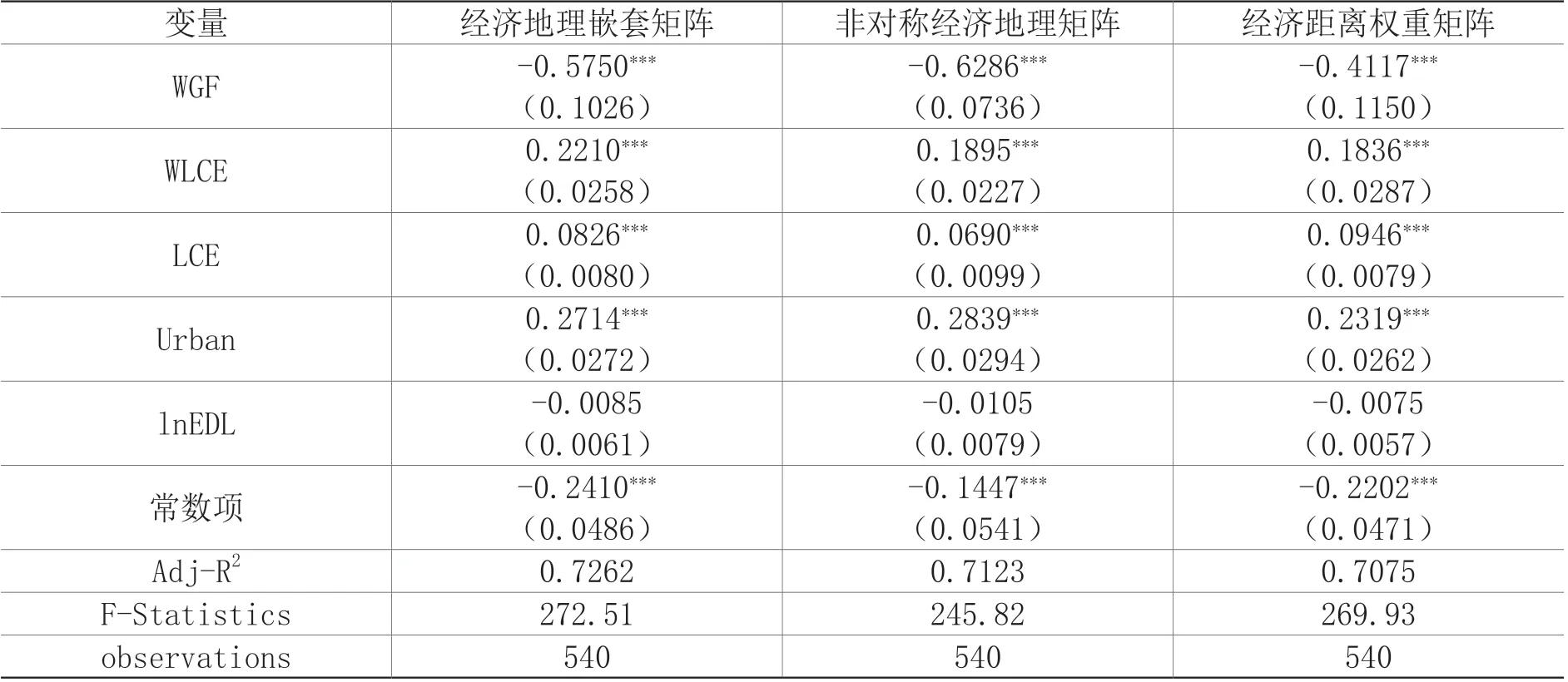
表6 绿色金融方程估计结果

对于绿色金融的空间滞后项而言，相邻省域的绿色金融发展对本地区绿色金融发展产生了显著的挤出作用。具体而言，在控制其他变量不变的条件下，邻近地区绿色金融指数每提升1个单位，本省绿色金融指数将降低约0.63个单位。对于低碳经济的空间滞后而言，在3种不同空间权重矩阵下，低碳经济的空间溢出效应在1%的显著性水平下显著。具体而言，以非对称经济地理矩阵为例，在控制其他变量不变的条件下，低碳经济每提升1个单位，绿色金融指数平均提升约0.19个单位。低碳经济对绿色金融产生了正向的空间促进效应，一个地区的低碳经济越发展则越有利于培育本地区绿色金融，同时助推了邻近地区绿色金融发展。但是，邻近地区的绿色金融发展与本地区绿色金融进程则是明显的空间竞争关系，这种负向溢出效应为地区间低碳政策协调配合、消除负外部性提供新的挑战。

（三）稳健性检验

本文运用广义空间三阶段最小二乘（GS3SLS）来考察绿色金融和低碳经济可能存在的双向内生关系。为了对模型进行稳健性检验，采用广义空间二阶段法（GS2SLSXT）重新对方程（11）和方程（12）进行估计。结果显示，模型中各变量符号未发生改变，数值大小未发生较大变化，并且显著性水平基本一致，这表明表5与表6的估计结果是稳健的②限于篇幅，未报告稳健性检验结果，备索。。

（四）绿色金融助推低碳经济转型的直接效应和间接效应分析

1.直接效应结果分析

绿色金融的直接效应：从表7可知，在三种不同的空间权重矩阵下，绿色金融对低碳经济转型都有显著的正向影响，并均通过1%的显著性检验。此外，估计系数十分接近，这从侧面反映出参数估计结果是稳健的。能源强度的直接效应：估计结果在5%的显著性水平下显著，能源强度与低碳经济存在负向变动的关系，高能耗对地区低碳经济转型起到明显阻碍作用。外商直接投资的直接效应：国外资本的进入对地区低碳全要素生产率起到负面影响，作用较微弱，这一结果在一定程度上支持了“污染避难所”假说。

2.间接效应结果分析

绿色金融的间接效应：从表7可见，绿色金融在两种矩阵下均能够显著促进邻近省份低碳经济指数的提升，并且通过了1%的显著性检验。但应注意的是，经济距离矩阵下的绿色金融估计系数明显小于经济地理嵌套矩阵下的回归系数。这意味着随着绿色金融的进步，邻近地区的低碳经济指数能够显著提升，但是将地理距离所蕴含的信息纳入到回归方程后，参数估计结果得到了一定程度上的修正。能源强度的间接效应：以非对称经济地理矩阵为例，绿色金融的回归系数在1%的显著性水平下显著，能源强度的提高有利于提高邻近地区的低碳全要素生产率。经济发展水平的间接效应：在三种不同权重矩阵下，系数估计结果均为负，且在5%的显著性水平下显著，这表明本地区经济发展水平的提高抑制了邻近地区的低碳经济转型。另外，从经济距离权重矩阵到经济地理嵌套矩阵，再到非对称经济地理矩阵，估计参数的绝对值逐渐减下，这表明综合考虑地理因素和经济发展差异的非对称影响后，本地区经济发展水平的提升对相邻地区低碳经济发展的抑制作用在逐渐弱化。

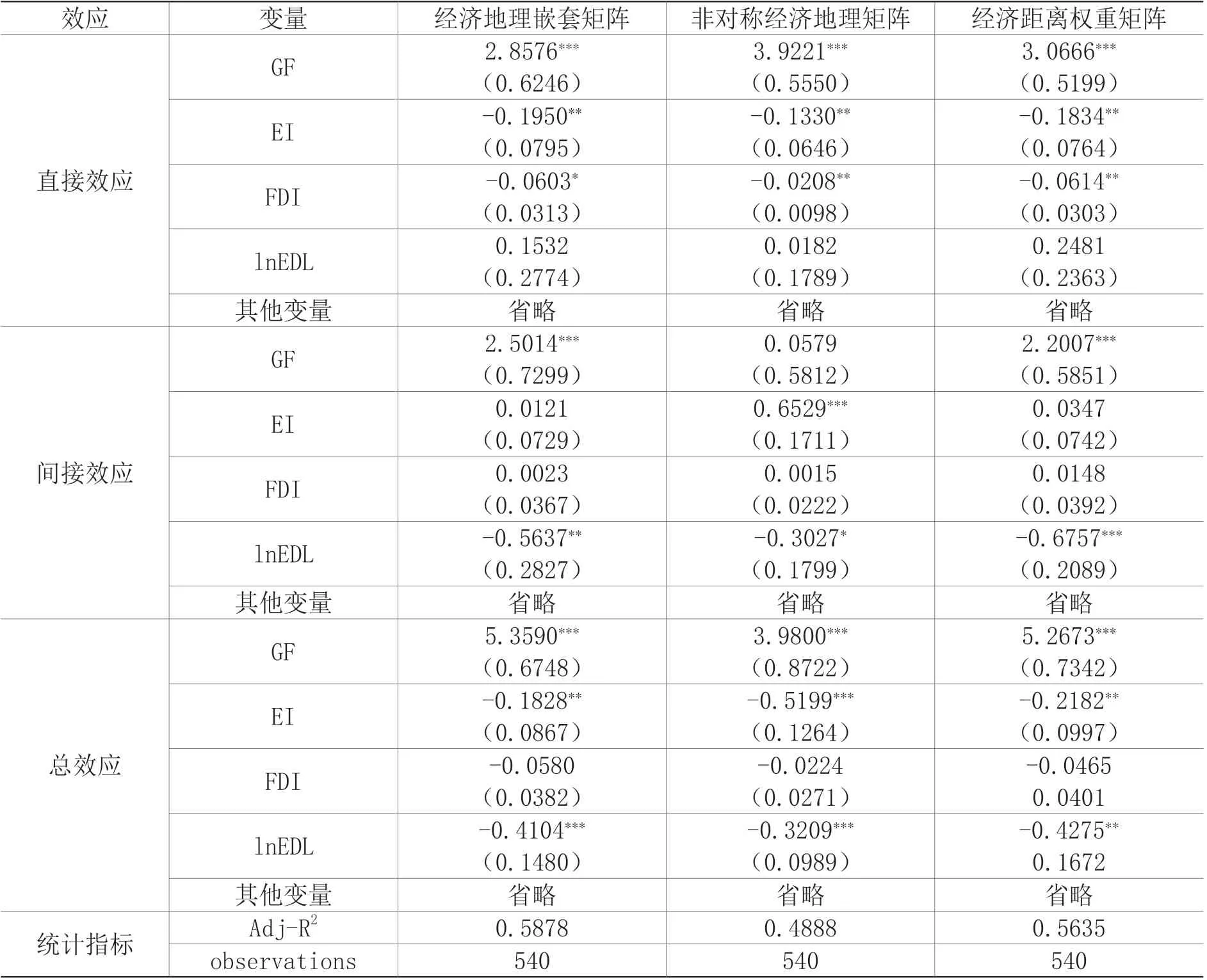
表7 绿色金融促进低碳经济转型的直接效应和间接效应估计

六、绿色金融推动低碳经济转型的条件性特征与阶段性特征

（一）条件性特征

为了进一步阐释在不同低碳经济指数水平下绿色金融影响低碳经济的条件性特征，建立面板分位数模型进行扩展分析，如式（13）所示。其中，X代表一系列控制变量。此外，核函数选择Epanechnikov，带宽确定采用Hall-Sheather法，估计方法运用核密度估计法。然后分别设置 25%、50%、75%的分位数，依次表示低碳经济指数的低水平、中水平以及高水平组，方程参数估计结果详见表8。

相较于最小二乘法（OLS）而言，分位数模型具备诸多优势。第一，更为细致地描述了条件分布，能够进一步展现条件分布的大致特征；第二，分位数回归并不苛求较强的分布假设，当面对扰动非正态的问题时，估计量要比OLS更加有效；第三，对存在异方差性的样本具备很强的适应性；第四，通过最小化加权误差绝对值、求和得到估计参数，有效规避了异常值对估计量的扰动，因此估计结果更为稳健。从表8可知，绿色金融对低碳经济的影响始终为正，并且随着分位点的提升，影响效应呈现出先减小、后增大的“U”型特征。这表明当低碳经济指数处在一个较低水准时，绿色金融发展有效推动了低碳经济进程；随着低碳经济指数提升，绿色金融的助推作用出现递减态势；而当低碳经济指数跨越50%的中间水平，这种正向促进作用愈渐强烈，呈现递增趋势。

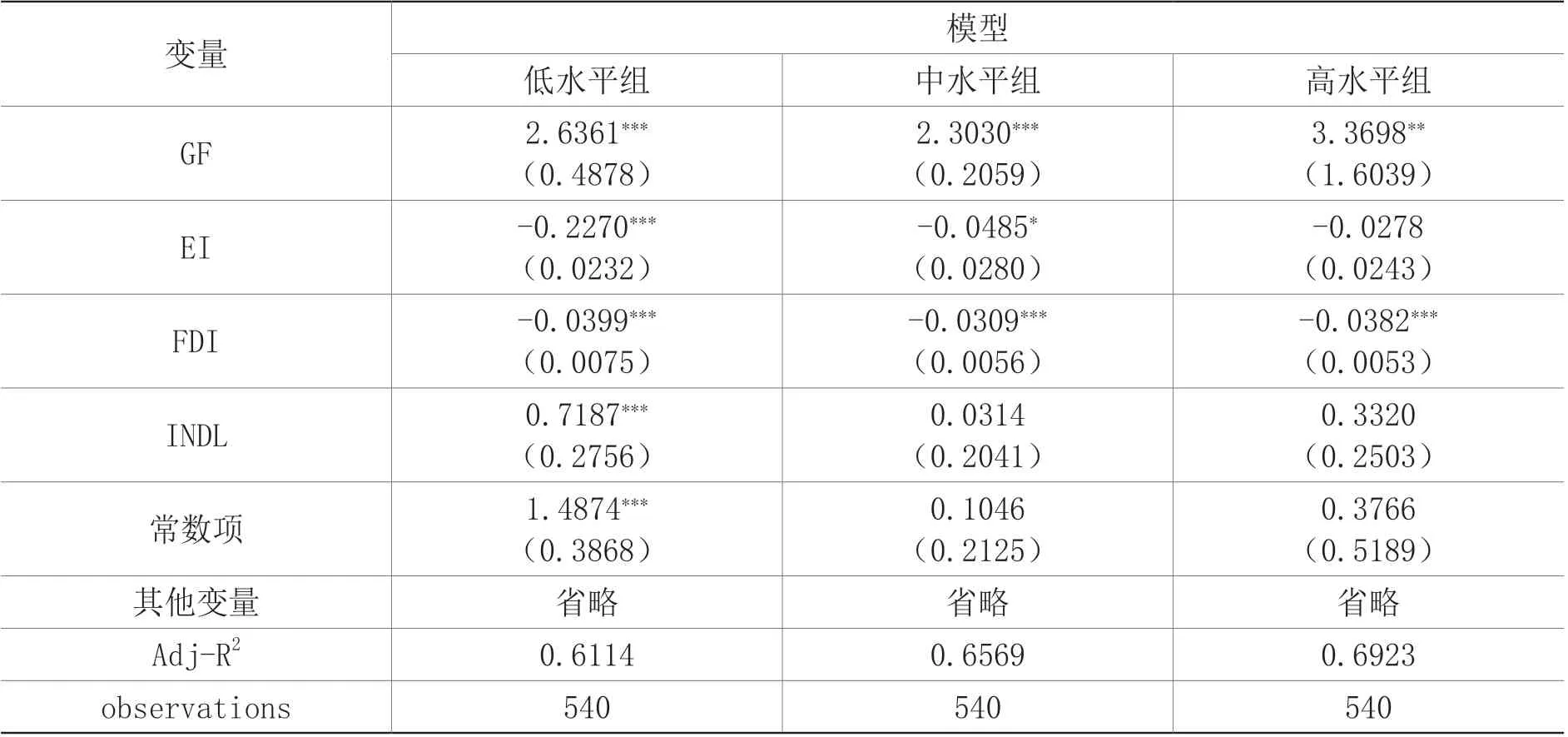
表8 面板分位数模型估计结果

（二）阶段性特征

为了进一步描述数字经济对我国实体经济影响的阶段性特征，故在分位数回归之后构建面板门槛模型。如式（14）-（16），GF表示绿色金融门槛变量，Urban表示城镇化水平门槛变量，INDL表示工业化水平门槛变量。I(·)表示示性函数，采用序贯检验（Sequential test）的方法对门槛值进行估计。

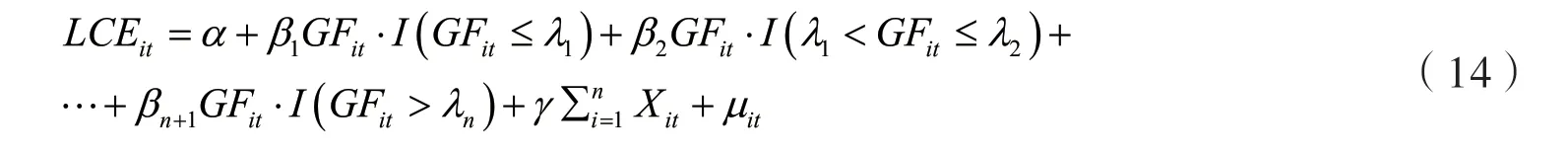
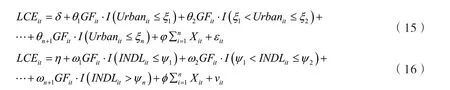
图3似然比函数图显示了3种不同门槛值的估计和置信区间的构造过程③限于篇幅，未报告门槛效应检验结果，如需备索。。对于绿色金融门槛而言，其门槛估计值为0.1812，95%的置信区间为[0.1792，0.1816]，当该门槛值处在对应的置信区间内时，其LR值小于5%显著性水平下的临界值（图3中虚线）。另外，95%置信区间的宽度较窄，这意味着门槛值的识别效果较好。城镇化水平门槛和工业化水平门槛的估计值分别为0.7640和0.1357，各自的95%置信区间分别为[0.7267，0.7801]和[0.1234，0.1395]，其他统计信息不再一一赘述。

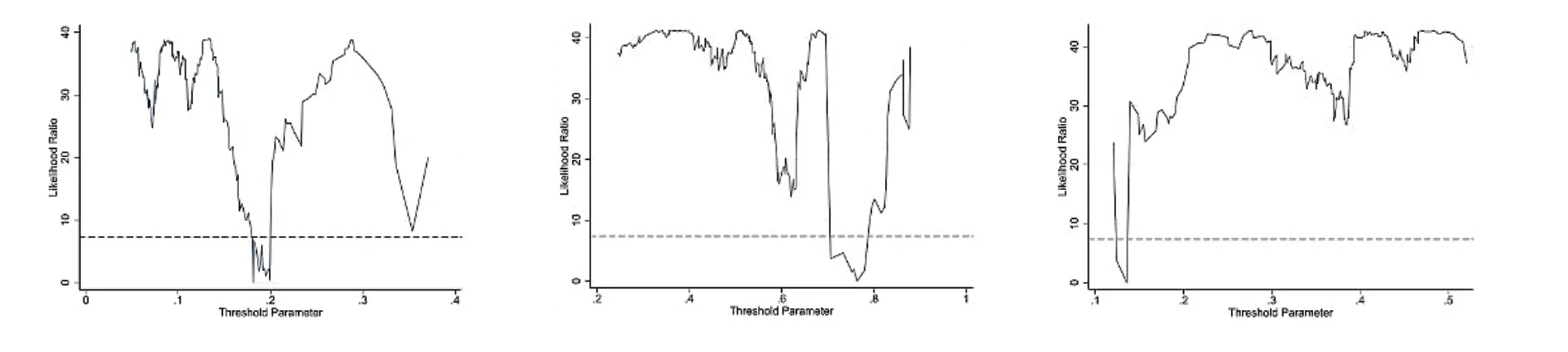
图3 门槛估计值与置信区间④从左至右依次为绿色金融、城镇化水平、工业化水平门槛对应的LR图。

模型回归结果如表9所示。根据估计结果，可以发现绿色金融对我国低碳经济的影响存在鲜明阶段性特征。

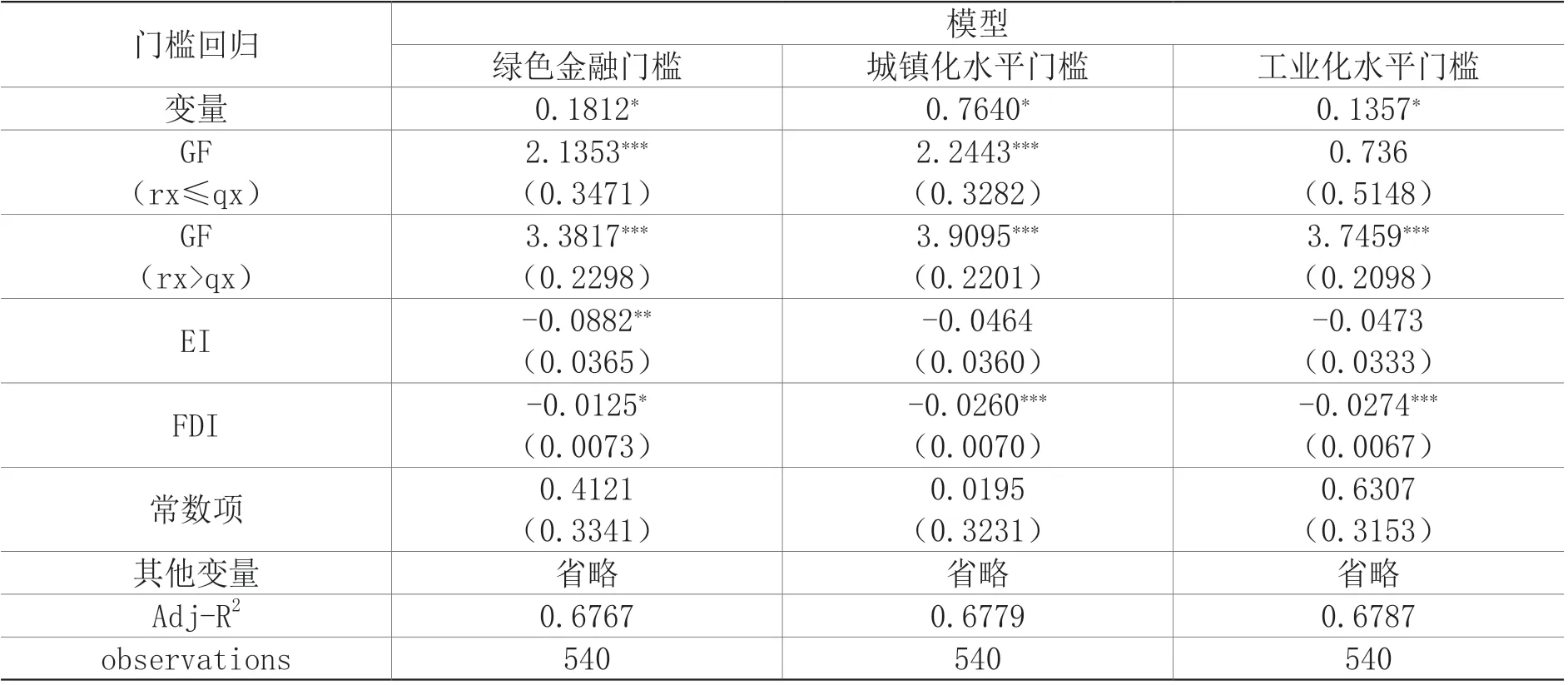
表9 面板门槛模型估计结果

1.绿色金融的门槛效应：当绿色金融指数小于0.1812时，绿色金融对低碳经济的促进作用为2.1353，在1%的显著性水平下显著。当绿色金融指数迈过门槛值0.1812后，绿色金融对低碳经济的促进作用达到3.3817，这意味着在具备一定的绿色金融发展基础后，绿色金融对低碳经济的助推作用更加能够被激发，考虑到我国各省绿色金融发展存在空间上的不平衡，经济落后地区与经济发达地区差异较大，因而绿色金融指数水平较低的省份更应加紧步伐，建设完善绿色金融基础设施与配套服务。

2.城镇化门槛效应：基于城镇化发展的不同水平，绿色金融对低碳经济的影响表现为两个截然不同的阶段。总体来看，在不同的城镇化水平下，绿色金融均有效促进了低碳经济转型。但当城镇化水平越过门槛值0.7640后，绿色金融对低碳经济发展的助推作用愈加明显，并且在1%的显著性水平下显著。绿色金融与低碳经济的关系呈现出明显的“阶段式跃升”的特点，这表明绿色金融与低碳经济间的关联与城镇化水平息息相关，城镇化进程愈是蓬勃发展，绿色金融愈加能够为低碳经济提质增效。

3.工业化水平门槛效应：经济联系亦体现出单门槛特征，当工业化水平小于门槛值0.1357时，绿色金融对低碳经济起到一定的助推作用，但不显著。当工业化水平跨越门槛值后，绿色金融对低碳经济的推动作用提高到3.7459且在1%的显著性水平下显著，这说明工业化水平的提升能够有效增强绿色金融对低碳经济的促进作用。根据经典的现代化理论，经济现代化的核心就是工业化，甚至可以将经济现代化等同于工业化，这表明现代化的本质就是依靠工业化驱动的现代社会发展变迁的过程。更应重视推进工业现代化进程，打造现代化工业体系，使得绿色金融支撑我国低碳经济转型的积极作用进一步释放。

七、结论与政策启示

本文基于中国30个省（市、自治区）2001-2018年的经济数据，运用空间杜宾模型、空间联立方程模型分析了绿色金融与低碳经济的交互影响以及空间溢出效应，并运用面板分位数模型和面板门槛模型分别刻画了绿色金融促进低碳经济转型的条件性特征和阶段性特征。研究发现：第一，绿色金融与低碳经济间存在显著的交互影响，两者之间是双向促进的关系，即绿色金融的发展能够有效推进本地区低碳经济转型，而低碳经济发展亦能有效拉动本地绿色金融进步。第二，绿色金融与低碳经济之间存在显著的空间溢出效应，具体而言：一是本地区的绿色金融指数与邻近地区的绿色金融指数显著负相关，同时本地的低碳经济发展与邻近地区的低碳经济显著负相关；二是邻近地区的绿色金融发展给本地低碳经济增长带来促进作用，而邻近地区的低碳经济规模的扩大亦对本地绿色金融发展带来正面助推作用；三是邻近地区的绿色金融发展对本地区绿色金融产生了显著的挤出效应，并且邻近地区低碳经济转型中对本地低碳经济亦产生了一定的抑制效应。第三，绿色金融对低碳经济的影响存在着显著的条件性特征和阶段性特征。

基于以上研究结论，提出如下政策启示：第一，应持续研究并健全绿色低碳发展政策，事中重落实、事后严监管，强化绿色金融与低碳经济的良性互动与协同发展。第二，应树立绿色金融发展全局战略思维，构建互利共生的区域金融发展格局。省份之间在政策制定方面应当加强沟通与协调，建立健全信息共享机制，减少信息不对称对低碳经济转型的负外部性，不断提升地区间绿色金融发展的政策配合度，逐渐消除绿色金融在蓬勃成长过程中的负向竞争性，进而使得整体经济效益最大化。第三，要及时解决我国各省级行政区在低碳经济转型进程中区域间不平衡、不充分问题，重点支持落后地区能源开发、农业生产、交通运输、工业制造、消费服务等方面的低碳化进程，加快低碳经济一体化进程，全力实现“双碳”目标。第四，加快培育低碳技术方面的优质人才，促进地区间环保机构、科研院所的沟通与合作，建立健全低碳发展共享机制，使绿色、低碳理念更全面深入融入到经济发展过程中，从而不断推动低碳经济走向更高水准。