固体的弹性模量和内耗测量方法研究进展

谢明宇 李法新

北京大学工学院力学与工程科学系, 北京 100871

1 引 言

弹性模量和内耗作为固体材料的基本力学性能, 其准确快速的测量方法非常基本和重要. 对于常见的各向同性材料, 弹性模量包括杨氏模量E、剪切模量G、体积模量K和泊松比μ, 这四个量中只有2 个是独立的, 其中使用最多的是E和G(徐芝纶 1979). 对于材料的内耗, 直观的描述是, 当一个构件自由振动时, 即使没有外界的阻尼, 振动也会随时间衰减下来, 也就是说, 材料本身也会耗散能量. 固体材料的内耗大致可以分为两类: 滞弹性内耗和静滞后内耗. 滞弹性一词是Zener (1948)提出的, 其特点是材料在加载和卸载时, 应变不是瞬时达到其平衡值, 而是通过某种弛豫过程完成其变化. 典型的弛豫过程包括由点缺陷引起的弛豫(Zener 1943, 1947; Nowick &Heller 1963)、由位错弦的阻尼运动产生的弛豫(Thompson & Holmes 1956, Alers & Thompson 1961) 以及由晶界滑动引起的弛豫等(Kê 1947, 1950; Kê & Mehl 1999). 根据Boltzmann 叠加原理,Zener 给出了各种滞弹性效应(蠕变、应力松弛、模量亏损、内耗)间的定量关系, 并由葛庭燧在多晶纯铝上通过实验验证(Kê 1947). 静滞后内耗产生于应力与应变之间存在多值函数关系,其大小与频率无关但与振幅密切相关(amplitude dependent internal friction, ADIF), 典型代表是钉扎位错脱钉过程引起的内耗(Granato & Lücke 1956, Bauer & Gordon 1960, Asano 1970). 在大多数情况下, 固体材料的力学行为是滞弹性(anelastic), 这与熟知的黏弹性(viscoelastic)有所不同, 固体材料的各种不同力学行为的分类见表1 (冯端 1999).

表 1 按应变(ε )−应力(σ )关系对固体材料不同力学行为进行分类

最早的弹性模量测量方法, 可以追溯到十七世纪虎克定律的提出, 即在准静态加载下采用测量力和变形的关系来确定材料的杨氏模量, 这就是在下一节要介绍的准静态测量方法. 从理论上说, 准静态方法也可以通过测量蠕变(Brook & Sully 1955, Ninomiya et al. 1963)和应力松弛(Sternstein & Ho 1972)曲线来得到固体的内耗, 但实际中一般不采用这类方法来测量内耗. 动态方法是常用的弹性模量和内耗测量手段, 按测量频率从低到高可分为低频法、共振法、波传播法. 对应于这些方法已经出现了一些商用的测量仪器, 如动态热机械分析仪(DMA)、共振柱测试仪、超声模量仪等. 需要指出的是, 对于结构硬材料如金属、陶瓷等, 其弹性模量随频率变化较小, 可以认为是常数. 而对于内耗(滞弹性内耗)来说, 它与测量频率有较强的相关性(Woirgard et al. 1977, Lee et al. 2000), 因此在讨论内耗时必须明确指出测量的频率. 目前, 弹性模量的测量方法已经比较成熟, 并且建立了通用的标准, 如ASTM E1875 和E1876 分别采用自由梁共振法和脉冲激励法来测量各向同性固体的杨氏模量和剪切模量, 其测量误差可以控制在5%甚至2%以内(Wolfenden et al. 1989, ASTME1875-13 2013, ASTME1876-15 2015). 相比之下, 目前内耗测量的准确度还差强人意, 对金属材料来说, 当前主要采用的扭摆法和自由梁振动衰减法的内耗测量误差均在10%以上. 内耗的准确测量迄今为止还是一个尚未解决的难题.

本文的内容安排如下: 第2 节总体介绍弹性模量和内耗测量的4 类方法, 即准静态方法、低频法、共振法、波传播法. 第3 节对常用的几种共振方法进行了详细介绍与评论. 第4 节重点介绍了本课题组最近提出的基于机电阻抗的模量内耗测量新方法. 最后, 对这种新的模量内耗测量方法的意义和应用前景进行了讨论和展望.

2 弹性模量与内耗测量的4 类方法

2.1 准静态方法

准静态法不仅可以根据应力-应变曲线的斜率来计算弹性模量, 同时还可以测量内耗(Blanter et al. 2010). 其测量方式分为以下两种: (1)测量应力-应变滞回曲线, 根据滞回环的面积ΔW来计算内耗; (2)利用准静态松弛试验测量内耗(测量恒定应力σ0下的蠕变效应ε(t)或者测量恒定应变ε0下的应力松弛效应σ(t)).

利用应力-应变滞回环面积测量内耗相对简单, 直接根据内耗的定义计算即可,其中ΔW是材料振动一个周期中所耗散的能量, 而W是材料中贮存的最大弹性能. 另外, 通过改变最大应变水平可以方便地测量与振动幅值相关的内耗(ADIF). 接下来主要阐明准静态松弛法,这里以蠕变为例, 如图1 所示. 当在零时刻瞬时施加恒定应力σ0后, 理想弹性体的应变会直接达到εU并保持恒定(下标U 代表未弛豫, unrelaxed); 滞弹性体的应变则是先瞬时到达εU, 接着通过某种弛豫过程渐渐增加直至饱和到达εR, (下标R 代表弛豫, relaxed); 线黏弹性体的应变则会趋于线性增长. 这里讨论的是滞弹性体, 定义滞弹性体的响应函数为:J(t) =ε(t)/σ0, 未弛豫弹性柔量为:JU=εU/σ0.那么根据玻尔兹曼叠加原理可以得到该滞弹性体在任意频率ω下的动态弹性柔量J(ω)的实部J1(ω)和虚部J2(ω) (冯端 1999)

图 1 弹性体的蠕变过程

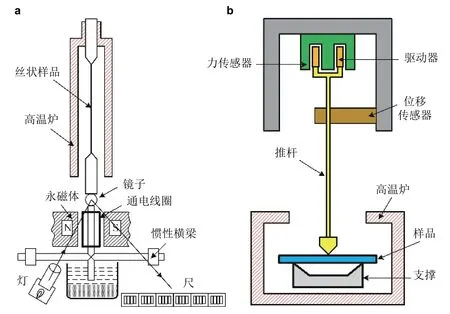
图 2 低频法测量弹性模量与内耗的装置.(a)扭摆仪,(b)动态热机械分析仪DMA

内耗可以根据动态柔量的虚部与实部的比值得到. 由于使用静态法测弹性模量与内耗对应力应变的测量精度要求较高, 所以导致其测量误差通常在10%以上(Nowick 2012), 因此它很少被使用.

2.2 低频法

低频法通过测量应力与应变之间的相位差来计算内耗, 其中最典型的两个方法就是扭摆法与DMA. 扭摆仪是我国著名物理学家葛庭燧院士提出的(Kê 1947, 葛庭燧 1994), 其主要结构如图2(a)所示. 被测样品通常呈细棒状或者丝状, 其一端用夹具固定, 另外一端通过夹具与横梁惯性体连接, 被测样品被置于高温炉或者低温恒温器中. 通过给放置在永磁体中的线圈施加电流从而产生扭矩, 利用光学杠杆测定微小角位移. 应力-应变之间的相位角是通过计时器测量负载信号和位移信号过零点之间的时间延迟来确定的. 对于一个高精度的扭摆, 如果计时器的测量精度为1 μs, 那么其在10 Hz 下的相位角测量不确定度为6.0 × 10-5(Lakes 2004). 但是为了达到这样的准确度, 必须有效的降低电子以及机械噪声. 商用DMA 的基本结构如图2(b)所示, 它通常使用电磁驱动器连接推杆给被测样品施加一个固定频率的振动(0.01 Hz ~ 100 Hz), 然后利用力传感器和位移传感器分别测量力和位移信号并根据它们之间的幅值关系与相位差来计算弹性模量与内耗. DMA 通常具有多种变形模式可供选择, 如拉压模式、剪切模式、三点弯模式等等(Salje &Schranz 2011).

图 3 波传播法测量材料的模量与内耗.(a)波传播法测量示意图,(b)超声波通过滞弹性的衰减过程

低频法最大优势在于其可以方便的测量不同频率以及应变幅值下的内耗, 但对于弱阻尼材料, 如金属、陶瓷等, 由于应力应变之间的相位差很小, 并且时常被噪声所掩盖, 因此必须有效的控制信噪比(Lakes 2004). 事实上, 测量弱阻尼材料的最好方法是共振法.

2.3 共振法

当外加激励的频率达到被测试样的共振频率时, 试样中连续反射的行波干涉形成驻波, 试样产生剧烈振动, 该振动的幅值不仅与外加激励成正比, 同时与试样的内耗成反比. 共振法是最古老也是应用最为广泛的弹性模量与内耗测量方法, 其测量精度一般高于其他方法. 按照测量内耗的方式, 共振法可以分为自由衰减法、功率补偿法、共振波形法. 按照测量装置是否与被测样品接触, 共振法又可以分为: 接触式与非接触式方法. 若按照激励共振的方式, 还可以分为: 压电晶体激励法、电磁激励法、静电激励法等等. 在本文的第3 节中将对目前常用的一些共振法进行详细的介绍.

2.4 波传播法

共振法在被测试样中形成驻波, 而波传播法(Rose 1999, ASTME494-10 2002, Periyannan &Balasubramaniam 2015)则采用更高频的扰动激励试样, 从而在试样某个方向上产生单一的脉冲或者一个波包, 如图3(a)所示. 该脉冲(波包)的中心频率远大于被测试样的共振频率, 且波长约为试样尺寸的1/10 甚至更小. 通过测量脉冲经过试样的时间(两个换能器一发一收测量), 或者测量脉冲经过试样一个端部再次返回的时间(单换能器脉冲回波测量)来计算波速, 接着根据波速与弹性常数的关系进一步计算模量. 至于内耗Q-1的测量, 如图3(b)所示, 可以根据相邻脉冲幅值的对数衰减以及脉冲的中心频率f换算得到

其中An与An+1是相邻脉冲的幅值,v是波速,L是波传播经过的长度. 最常用的波传播法就是利用较小尺寸的换能器在较大的各向同性的试样中激励出膨胀波与剪切波来测量弹性模量与内耗,此时被测样品的波速与弹性常数之间满足以下关系

其中v1和v2分别是膨胀波波速和剪切波波速,ρ是密度,E和G分别为杨氏模量与剪切模量,µ是泊松比. 波传播法的测量误差一般比共振法大得多(Nowick 2012), 并且由于被测试样的几何频散,以及波在试样边界的反射透射会导致内耗的测量值较真实值偏大(Lakes 2004).

3 几种共振方法的原理与特点

3.1 自由梁共振法和脉冲激励法

自由梁共振法(free-free beam)和脉冲激励法(impulse excitation technique)是测量材料弹性模量的两个标准方法, 分别被ASTM E1875 和ASTM E1876 收录(ASTME1875-13 2013, ASTME1876-15 2015). 这两种方法的本质都是通过激励长条状样品的弯曲振动(扭转振动)来测量杨氏模量(剪切模量). 其中, 长条状样品的杨氏模量E与一阶弯曲共振频率ff、剪切模量G与其一阶扭转共振频率ft满足以下关系

其中m是样品质量.b,t,L分别是长条状样品的宽度, 厚度与长度.T1是一个与泊松比有关的修正系数.B与A则是与被测试件宽厚比有关的系数.

如图4(a)所示, 自由梁共振法一般采用两根悬线悬挂样品并同时用于激励与接收振动信号.通过改变悬线的悬挂方式从而选择激励弯曲振动或者扭转振动. 悬挂点通常在样品一阶振动模态的两个节点附近. 一根悬线连接驱动换能器, 另一根悬线则连接接收换能器. 通过扫频信号来激振样品, 根据测量的幅频特性曲线可以得到一阶谐振频率ff或ft, 将其代入式(4)后即可以得到弹性模量. 与此同时, 该弹性模量相对应的内耗可以根据幅频特性曲线的半带宽得出. 被测样品通常要求表面平整, 上下表面拥有较好的平行度, 且一阶弯曲谐振频率控制在1 kHz ~ 10 kHz, 而一阶扭转谐振频率则控制在10 kHz ~ 30 kHz (ASTME1875-13 2013). 对于高低温环境下的测量,只需要选择适当的悬线将被测试件悬置于高温炉或低温恒温器中即可.

如图4(b)所示, 不同于自由梁共振法的连续扫频激励, 脉冲激励法(IET)采用轻微的机械冲击来激励样品. 通过对采集的时域信号进行傅里叶变换即可得到样品的一阶弯曲(扭转)共振频率. 样品的内耗可以根据半带宽得出, 或者也可以通过拟合下式给出(Roebben et al. 1997)

图 4 (a)自由梁共振法,(b)脉冲激励法

其中x(t)是接收的时域信号,fi是通过傅里叶变换得到的各阶谐振频率,Ai和φi是幅值和相位. 衰减指数ki与内耗的关系为:=ki/ ( πfi).

自由梁共振法和脉冲激励法的优点在于装置简单, 通用性强, 特别是自由梁共振法, 高低温下的测量装置几乎与常温一样, 除了激励和接收振动的难度会有所增加. 但是这两种方法的测试精度受悬挂(支撑)点的位置以及条状被测试件上下表面的平行度影响较大(Nowick 2012).

3.2 超声共振谱方法

传统的共振法测量弹性模量与内耗都是基于特定形状的试件产生单一种类的振动来完成的,在此情况下, 试件的谐振频率与被测弹性常数之间具有简单对应关系. 但是, 若要测量各向异性样品的弹性常数矩阵Cij, 传统方法就会显得力不从心, 而近三十年来发展起来的超声共振谱方法(resonant ultrasound spectroscopy, RUS)就能解决这个问题(Migliori et al. 1993, Leisure & Willis 1997). RUS 通过测量单一各向异性样品的频谱来反演所有弹性常数(弹性常数矩阵). 图5(a)是一个典型的RUS 测量示意图. 其中被测样品的几何形状通常是长方体、圆柱体或者球体. 被测样品的两个顶点被轻轻地夹在两个压电换能器之间, 从而确保边界自由的条件. 驱动换能器用于激励扫频信号, 接收换能器则用于感应样品的响应. 当驱动换能器的频率达到样品的一个共振频率时, 接收换能器就能观察到较大的响应. 图5(a)中显示了一个典型的测量频谱图.

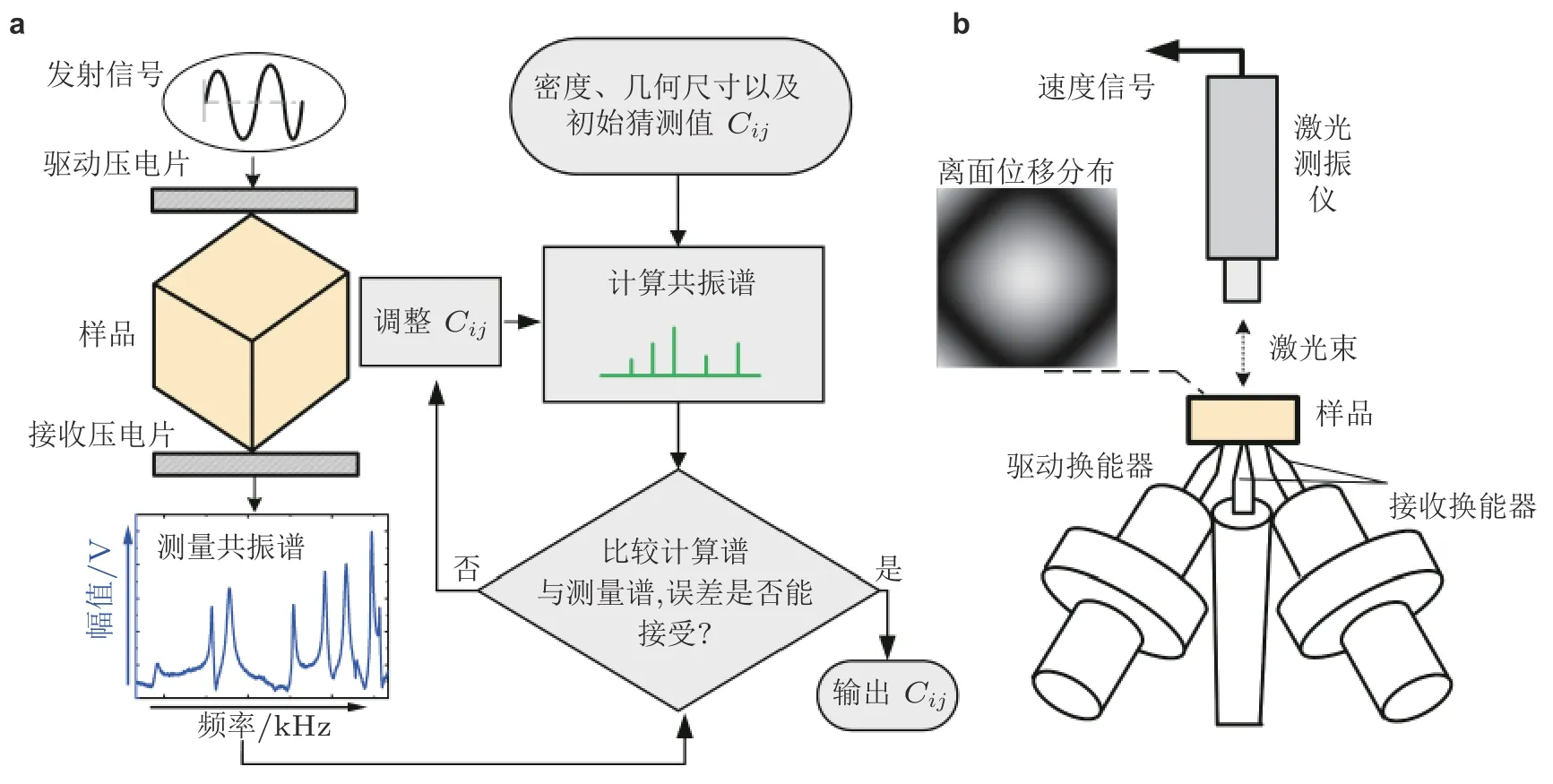
图 5 超声共振谱法RUS.(a)RUS 测量各向异性样品弹性常数矩阵示意图,(b)在RUS 中利用激光测振仪扫描离面位移进行模态识别(Ogi et al.2002)

根据测量得到的频谱反演被测试件的弹性常数的流程如图5(a)所示, 其主要分为两个步骤.首先对于给定尺寸、密度以及初始弹性矩阵Cij的被测试件在无外载的条件下运用Lagrangian变分原理, 然后通过求解以下广义特征方程得到试件的各阶共振频率

其中E是广义质量矩阵,Γ是广义刚度矩阵. 当被测试件具有正交或者更高晶体对称性时, 还可以根据位移的对称性把E矩阵和Γ矩阵分为8 个子矩阵来分别计算, 从而显著加快运算速度(Ohno 1976). 接下来将计算得到的共振频率与测量得到的频率做比较, 当二者误差不满足容许误差时, 利用Levenberg-Marquardt (L-M)算法(Press et al. 1986)来反演一组新的弹性常数. L-M算法的本质是牛顿迭代法与梯度下降法的结合. 经过多次循环迭代后就可以得到被测样品的真实弹性常数矩阵.

尽管RUS 可以通过一次测量获取样品的所有弹性常数与内耗, 但是它却拥有三个致命缺陷(Balakirev et al. 2019): (1)被测样品的品质因数Q不能太小(通常需要Q＞ 300), 否则频谱中各模态的峰混叠在一起; (2)测量频谱的模态遗漏给求解反问题带来很大麻烦. 其解决办法一般是调整被测样品多测几次, 或者对比计算的频谱手动增加缺失的模态频率, 但这非常考验测试人的经验(Leisure & Willis 1997); (3) L-M 反演算法对迭代初始值依赖性非常高, 当初始值远离真实值时, 迭代可能不收敛, 甚至收敛到某个伪结果上, 因此当测试人对所测样品的弹性常数的大小一无所知时, RUS 很可能失效. 事实上, 解决问题(2)和(3)最好的方法就是除了测量样品的频谱外, 还要识别出每一个频率所对应的振动模态. 如图5(b)所示, Ogi 等(2002)利用激光测振仪扫描测量长方体样品的一个面的离面位移分布图案来识别各个谐振频率所对应的模态, 但这大大增加了测量时间与成本.

3.3 压电超声复合振动技术

压电超声复合振动技术(piezoelectric ultrasonic composite oscillator technique, PUCOT)是一种比较古老的测量技术. 早在1925 年, Quimby (1925)对18.5° X 切α-石英振荡器驱动的任意长度的杆的纵向振动进行了理论分析, 并通过测量振荡器-杆复合系统的频率与端部速度来计算杨氏模量与内耗. Zacharias (1933)在Quimby 的工作基础上做出了改进, 他提出根据石英振荡器的导纳来计算杨氏模量与内耗. 虽然他们可以通过迭代算法求解被测试件的弹性模量, 但是内耗的精确表达式并不能给出. 到了20 世纪50 年代, Marx (1951)在谐振系统中加入第二块石英振荡器并与第一块石英振荡器组成半永久单元. 如图6 所示, 这两块振荡器一个作为驱动单元(drive), 另一个作为监测单元(gauge). 石英振荡器与被测试件的长度需要根据它们在常温下的弹性模量精心设计从而满足频率匹配条件, 即组合系统中的应力波的反节点需要通过各单元的连接点, 换句话说, 各单元中需要包含整数个半波长. 当在石英驱动单元上施加一个交流电压Ud后, 通过测量监测单元上的电压Ug的谐振频率与幅值就可以得到被测试件的谐振频率、内耗和最大应变.Robinson 等根据等效电路理论推导了系统的总内耗以及各组分的最大应变的表达式(Robinson & Edgar 1974, Schaller et al. 2001)

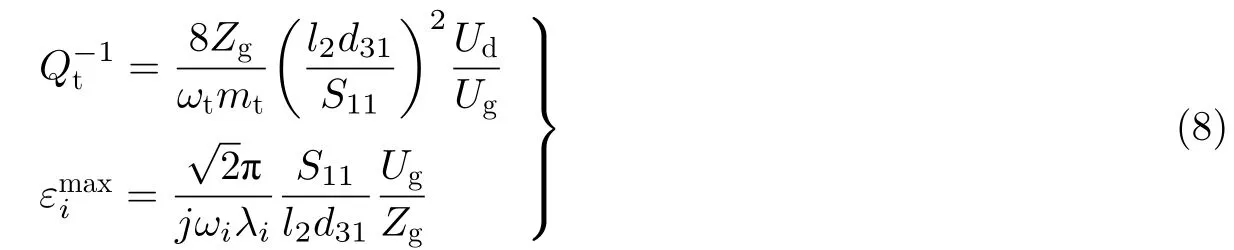
其中Zg是监测单元的(Gauge)电阻抗,mt和ωt是系统总的质量以及谐振频率(ωt≈ωi).S11和d31是X 切α-石英振荡器的弹性柔顺系数以及压电系数,l2是石英振荡器镀电极面的宽度,λi是组分i中的纵波波长. 被测试件的内耗与谐振频率通过以下表达式给出

其中mi,ωi和是第i组分的质量, 谐振频率与内耗. 由于石英振荡器的背景内耗非常小(约10-6),因此PUCOT 对于内耗的测量精度较高. 除了图6 所示的纵振动型PUCOT 外, Robinson 还提出了扭转型的(Robinson et al. 1974)以及弯曲型的(Devine & Robinson 1998) PUCOT 用于测量材料在不同振动模式下的内耗.

图 6 三组分压电超声复合振动技术

图 7 基于机电阻抗法的M-PUCOT 测量系统

对于高温与低温环境下的测量(Marx & Sivertsen 1953, Sutton 1953, Weertman & Salkovitz 1955), 需要在被测试件与石英振荡器之间插入一段频率匹配的熔融石英棒用来隔热. 被测试件插入到高温炉或者低温恒温器中, 石英振荡器则保持在恒定温度范围内. PUCOT 的一个重要优势在于它可以测量与应变幅值相关的内耗(amplitude-dependent internal friction)(Kustov et al.1998, 1999), 并且最大应变幅值在10-12~ 5 × 10-4范围内可调(Robinson & Edgar 1974), 这为研究材料由于塑性变形(Sapozhnikov et al. 2000)与疲劳损伤(Mason 1956, Golovin et al. 2004)产生的非线性内耗提供了重要帮助.

需要指出的是, PUCOT 采用了两个石英振荡器作为激励与接收装置. 然而, 由于石英晶体的压电性很弱, 而且共振峰很窄, 因此需要在石英振荡器和试样之间进行频率匹配, 也就是说, 需要在设计试件尺寸时知道试样的弹性模量. 因此, PUCOT 不能用来测量弹性模量未知的材料. 这或许是PUCOT 一直未能得到广泛应用的一个重要原因. PUCOT 主要用于测量已知模量材料温度相关的内耗, 但由于石英棒与样品之间需要比较严格的频率匹配, 而金属的模量随温度变化往往比较大, 因此PUCOT 测量金属内耗的温度范围往往比较窄. 另外, 由于石英扭转振荡器(Robinson et al. 1974)的性能沿环向分布不均匀, 因此利用PUCOT 测量扭转内耗存在一些问题.

终上所述, 目前弹性模量的测量方法已经比较成熟, 也形成了比较实用可靠的标准, 存在的主要问题是测量过程还不太方便快捷. 而内耗的测量无论在学术界还是工业界都尚未普及, 尤其对于金属、陶瓷等结构材料来说, 目前还缺少准确可靠的内耗测量方法.

4 基于机电阻抗的弹性模量内耗测量新方法(M-PUCOT 或Q-EMI)

最近, 本课题组提出了一种基于机电阻抗法的模量和内耗测量方法, 称之为M-PUCOT(modified piezoelectric ultrasonic composite oscillator technique)(Xie & Li 2020a). 该方法也可称为定量的机电阻抗法Q-EMI (quantitative electro-mechanical impedance), 以区别于结构健康监测领域的定性EMI 方法(Ayres et al. 1998, Fu et al. 2015). 该方法可以准确、快速、同时测量出材料的模量和内耗, 将模量和内耗的测量变成了一种通用工具, 从而可以用力学性能的变化来表征所有固体材料的内部演化, 如固态相变、玻璃态转变、位错运动、晶界滑动、内部损伤等等.

4.1 测量原理

如图7 所示, M-PUCOT 摒弃了PUCOT 中的一对石英棒振荡器, 取而代之的是一片小的锆钛酸铅(PZT)压电圆环(内径d, 外径D, 厚度h). 该压电圆环不仅用于激励振动信号也用于接收振动信号. 由于PZT 具有很大的压电系数与机电耦合系数, 因此压电圆环换能器与被测样品之间的频率匹配条件不需要满足, 并且压电环的厚度h远小于隔热棒的长度lS以及样品的长度lM,而压电环的外径D与隔热棒以及样品的直径一致. 当需要测量杨氏模量EM及其对应的纵振动内耗时, 采用d33 模式纵向振动型压电圆环, 该圆环沿厚度方向极化, 其上下两个底面为电极面, 当把压电圆环-被测样品(或压电圆环-隔热棒-被测样品)粘接并沿圆环厚度方向施加交变电场时, 整个系统即可产生纵向振动. 当需要测量剪切模量GM及其对应的扭转振动内耗时,则采用d15 模式的扭转型压电圆环(Xie et al. 2020). 扭转型压电圆环的制备流程如下: 首先将厚度极化的压电圆环的上下两个电极面磨去. 接着将其沿直径均匀地切割成两个半圆环, 并在4 个切割面喷制电极. 然后将其中一个半圆环反向, 使得两个半圆环的极化方向相反, 并用导电银胶将它们粘接组成一个新的圆环. 最后沿该圆环的环向施加交变电场后即可产生均匀的扭转振动.

对于常温下测量弹性模量与内耗, 可以直接将压电圆环换能器与被测试件粘接组成双组分系统. 而对于高低温环境下的测量, 与传统的PUCOT 类似, 还需要在换能器与被测样品之间插入一段频率匹配的熔融石英棒或氧化铝棒来隔热, 从而保证换能器工作在合适的温度范围内. 被测试件插入到高温炉或者低温恒温器中保证恒定温度. 由于熔融石英隔热棒或氧化铝棒具有极佳的热稳定性, 因此其内部温度梯度对其弹性模量以及内耗造成的改变在600 ℃以内可以忽略不计(Marx 1951), 当测量温度到达600 ℃以上时, 通常需要进行标定消除其影响. 与传统的共振法测量系统的幅频特性曲线不同, 这里利用阻抗分析仪连接换能器后测量系统的电纳曲线(导纳曲线的虚部), 通常一条电纳曲线的测量速度在1 ~ 2 s. 根据电纳曲线的m+n阶谐振频率与反谐振频率来计算弹性模量与内耗. 其中m是隔热棒中的半波长数,n是被测试件中的半波长数. 由于电纳曲线的斜率只与换能器的参数有关, 因此还需要将电纳曲线的斜率抹平后来获得准确的谐振频率与反谐振频率, 如图7 中的插入图所示. 由于压电环的厚度远小于样品及隔热棒的长度, 样品的杨氏模量、剪切模量以及对应的两种内耗可以由系统的谐振频率和反谐振频率显示地求出, 其表达式如下

其中ρP,ρM,ρS分别是压电环、被测试件、隔热棒的密度.lP,lM,lS分别是压电环、被测试件、隔热棒的长度;ES,, 分别是隔热棒的杨氏模量, 纵向振动内耗, 剪切模量以及扭转振动内耗. 由于隔热棒的内耗非常小(~10-5), 因此通常可以当作零. 对于三组分系统(换能器-隔热棒-被测试件), 通常采用n= 1,m= 1 或2. 对于双组分系统, 把lS= 0,m= 0 代入式(10)后, 可以得到双组分系统的模量内耗计算表达式

为了验证上式的准确性, 利用激光测振仪测量了双组分系统(换能器-被测试件)的端部位移的幅频特性曲线并与其电纳曲线作对比, 如图8 所示. 可以看出电纳曲线的谐振点与反谐振点分别对应于位移幅频特性曲线的两个-3 dB 点, 而它们的平均值刚好为幅频特性曲线的峰值点. 此时传统的内耗定义Q-1=与上式的内耗表达式(11)不谋而合, 从而证明了公式的准确性.

图 8 换能器−被测试件双组分系统的电纳曲线与端部位移幅频特性曲线

另外值得一提的是, 式(11)中的内耗表达式不局限于对规则圆柱体的测量. 事实上, 对于具有任意形状与任意边界条件的结构体, 当其与某压电体粘接后(压电体具有任意形状与振动模式), 通过测量系统抹平斜率后的电纳曲线的谐振频率与反谐振频率, 再代入式(11)后即可求得系统的内耗. 当压电体足够小, 且边界条件不引入额外损耗时, 此时测量的系统内耗即可认为是结构体本身的. 因此, 可以利用该方法对结构内耗进行方便监测.

4.2 测量的重复性和快速性

相比于之前的模量内耗测量方法, 基于机电阻抗法的M-PUCOT 的最大优势是测量的高度重复性和快速性. 图9 是用两个名义上相同的压电圆环换能器A 和B 对同一个金属棒进行的4次测量结果. 从图9 中可以看到, 即使采用两个不同的压电圆环换能器, 共振频率的测量重复误差也小于0.1%, 模量测量重复性误差小于0.2%, 内耗测量的重复性误差小于3%. 相比之下, ASTM现行标准E1875(自由梁振动法)测量杨氏模量的重复性误差最好仅可以控制在2%以内. 因此,基于机电阻抗法的M-PUCOT 的测量准确性比ASTM 现行标准高一个量级. 另外, 测量图9 中的一条电纳曲线只需2 s 左右. 由于M-PUCOT 的快捷性和准确性, 它将模量和内耗的测量变成了一种工具, 从而可以通过测量力学性能的变化来研究材料的内部演化.

图 9 采用M-PUCOT 方法测量金属棒杨氏模量和内耗(纵向振动模式)时得到的电纳曲线.(1)采用压电换能器A 的第一次测量;(2)采用压电换能器A 的第二次测量;(3)将换能器A 取下,再次粘结后的测量结果;(4)采用另外一个换能器B 的测量结果

4.3 典型应用

M-PUCOT 测量速度快, 分辨率高, 非常适合用于材料的相变研究. 图10 显示了利用M-PUCOT 的纵向振动模式测量轴向极化PZT-5H 的弹性模量以及纵向振动内耗(Xie & Li 2020b). 可以看到,在居里温度(190) 之前,随着温度的上升电纳曲线的谐振频率与反谐振频率的平均值缓慢上升, 代表了弹性模量的缓慢增加, 而反谐振频率与谐振频率的差值则是缓慢减小, 表明了内耗缓慢降低; 当接近居里温度时,谐振与反谐振频率迅速降低, 而其差值迅速增大, 代表了材料在接近相变点时模量的迅速减小以及产生的内耗峰;当温度超过居里温度后, 模量又迅速增大,内耗则迅速减小直至饱和.

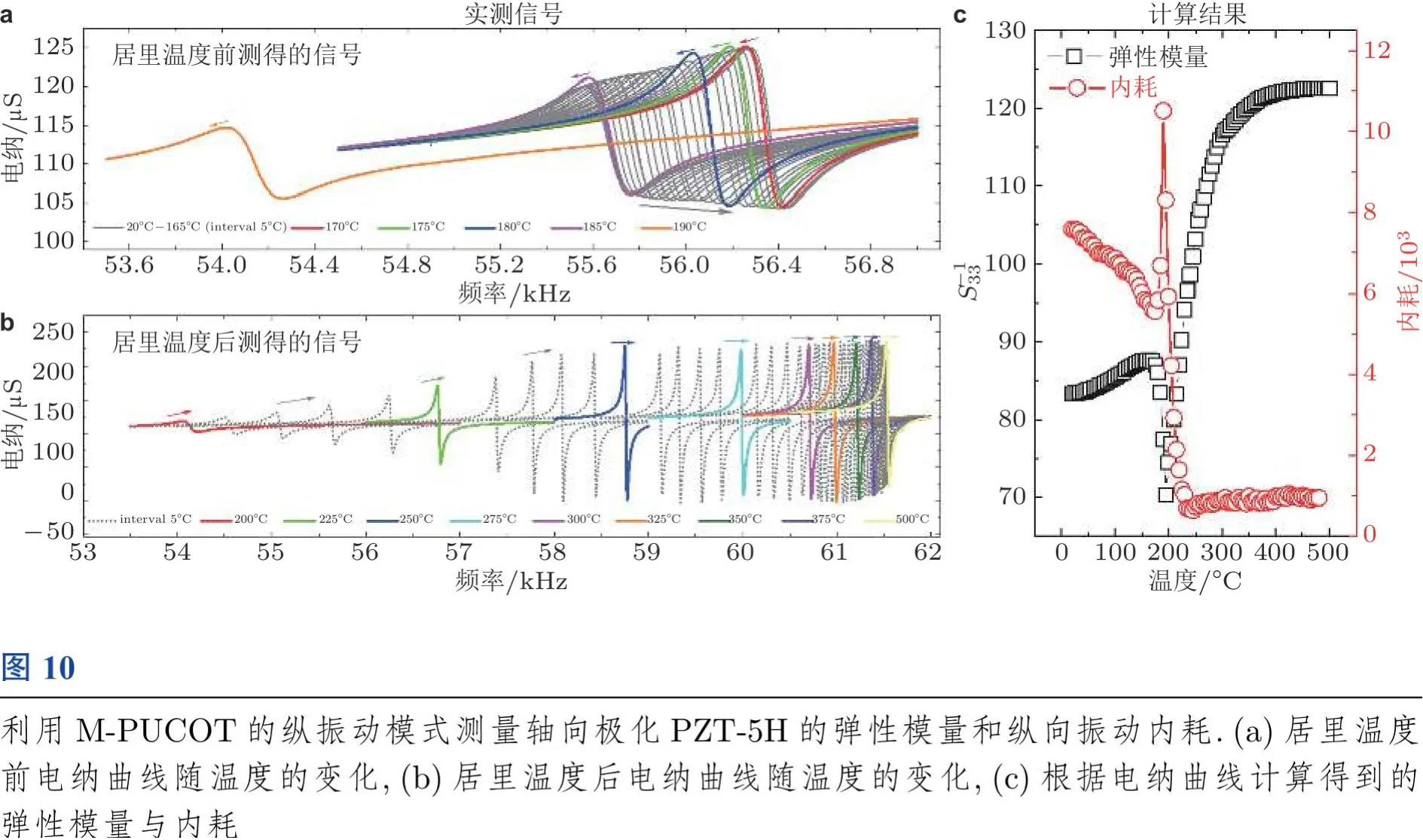
图11(a) 显示了利用M-PUCOT 测量大块金属玻璃Zr41.2Ti13.8Cu12.5Ni10Be22.5玻璃化转变与晶化过程中的弹性模量与内耗的变化(Xie et al. 2021). 可以看出,当温度达到初始玻璃化温度Tx 时(375 ℃), 大块金属玻璃进入过冷液相区, 结构发生弛豫,导致其弹性模量降低以及内耗迅速增加.当温度达到初始晶化温度Tg (440 ℃) 时,弹性模量达到最小值,约为初始值的90%, 同时出现明显的内耗峰. 结合图11(b) 可以发现: (1) 当大块金属玻璃进入过冷液相区(约410 ℃) 后再降温,弹性模量微弱增加, 而X-射线衍射(XRD) 图没有变化. 说明模量的增加不是局部结晶导致的, 而是自由体积的湮灭造成的;(2) 当温度达到60 0℃以上时,完全结晶,材料表现出晶体的性质, 即弹性模量随温度上升而下降, 内耗呈指数增加(高温背景内耗).

除了研究材料温度相关的模量和内耗变化, M-PUCOT 还可以通过测量模量和内耗的变化来预测材料内部的损伤程度. 为验证这种方法的有效性, 对房山汉白玉岩石在压缩破坏过程中进行了模量和内耗的测量(Xie & Li 2020c). 图12 是岩石在压缩过程中典型的应力- 应变曲线, 从图中可以看出该岩石的强度比较低, 强度分散性比较大, 约为20 ~ 35 MPa.

图 11 利用M-PUCOT 测量大块金属玻璃Zr41.2Ti13.8Cu12.5Ni10Be22.5 玻璃化转变与晶化过程中的弹性模量与内耗.(a)循环升温与冷却过程中的弹性模量与内耗随温度的变化,(b)不同温度热处理后金属玻璃的XRD 图案

图 12 房山汉白玉岩石在压缩过程中的典型应力应变曲线

图13 给出3 个不同的岩石样品在压缩到破坏前, 杨氏模量、纵振动内耗、剪切模量和扭转内耗的变化情况. 可以看到, 对3 个样品来说, 杨氏模量基本上随压应力的增大而增大, 而剪切模量变化不大. 纵振动内耗(longitudinal IF)变化不规律. 而扭转内耗随着压应力的增大单调上升,在破坏之前, 扭转内耗为加载前的1.6 ~ 2.4 倍, 这是由于随着压应力的增大, 材料中的微裂纹不断增加, 从而增加了扭转内耗. 根据图13 中的结果可以预测出, 测量材料的扭转内耗, 有望对材料的内部损伤程度进行有效的评估.

图 13 房山汉白玉岩石在压缩破坏前的模量和内耗变化.(a)1 号样品,(b)2 号样品,(c)3 号样品

5 总 结

从前面的回顾可以看出, 弹性模量和内耗的测量方法在几十年前就遇到了技术瓶颈, 近些年来发展缓慢. 弹性模量的测量方法相对比较成熟, 存在的主要问题是测量还不够方便和快捷; 内耗的测量还未形成稳定可靠的方法, 尚未普及应用. 本文回顾的四大类模量和内耗测量方法, 对于模量测量来说, 最常用的是共振法; 对于内耗测量来说, 之前常用的是低频法, 以葛氏扭摆和DMA 为代表.

本课题组最近提出的基于机电阻抗的模量内耗测量方法M-PUCOT, 可同时、准确、快速地测量杨氏模量、剪切模量及相应的内耗, 相比之前的模量内耗测量方法具有显著的优势. 该方法已经、正在或将要改变相关领域的研究:

(1)M-PUCOT 属于高频电测方法, 其测量模量的重复性精度比现有的ASTM 模量测量标准(自由梁振动法E1875, 脉冲激励法E1876)高一个量级, 测量时间只需几秒, 可以预见在不久的未来将取代ASTM 现有标准, 成为最常用的模量测量方法;

(2)M-PUCOT 无需传感器和样品之间频率匹配, 可在非常宽的温度范围内实时、准确地测量模量和内耗, 它将模量和内耗的测量变成了一种通用的手段, 可以很方便地研究固体的高温/低温力学行为, 包括通常材料的模量降低、相变、玻璃态转变等;

(3)M-PUCOT 测量金属材料的内耗具有独到的优势, 内耗测量的绝对误差可以控制在2E-5以内. 内耗对于材料的损伤、疲劳等力学性能劣化非常敏感, 测量内耗将成为判断材料疲劳、损伤的有效手段. M-PUCOT 方法有望开辟金属材料疲劳、损伤研究的新局面.

致 谢本文工作得到国家自然科学基金重大项目课题 (11890684) 的资助.