基于GEP、ANFIS、MARS和GBDT模型构建浙江省极端降雨事件预测模型

沈 黎

(杭州市富阳区水文水资源监测管理中心，浙江 杭州 311400)

受到气候变化及人类活动的加剧，浙江省降水已呈现出了日渐极端的趋势[1]。JUNG等和KARAGIANNIDIS等分别在韩国和欧洲分析了当地区域的极端降水事件变化趋势，均指出了区域极端降雨发生频率呈现显著增加趋势[2- 3]。极端降雨事件的发生造成了洪涝灾害现象十分频繁，对居民安全及经济发展产生了十分恶劣的影响[4- 5]。极端降雨事件指的是降水高于(或低于)观测值区间的上限(或下限)，国际上普遍采用极端降雨指数来描述区域极端降雨事件并分析区域的极端降雨变化趋势。因此，研究区域极端降雨事件的变化规律对区域防洪政策的制定具有十分重要的意义。

目前，针对区域极端降雨指数变化规律的研究已取得了一定的进展。杨家祯等[6]通过计算广西省1951—2015年的11种极端降雨指数，分析了广西省极端降雨事件的发生规律，指出11种极端降雨指数均呈现出从广西东北及南部向西南、西北递减的变化趋势；张俊等[7]研究了长江流域1961—2017年极端降雨指数的变化规律，指出不同年代长江流域极端降雨事件发生规律有所不同，2000年以后，长江流域极端降雨事件有所增加；苗正伟等[8]分析了京津冀地区1961—2017年的极端降雨事件变化规律，指出了在该时间段内京津冀地区气候呈现干旱化趋势。

虽然，针对极端降雨指数分布规律的已有了部分研究成果，但这些成果基本集中在分析现存数据规律上，针对区域极端降雨指数预测模型的研究仍然较少。随着人工智能及机器学习模型的兴趣，基于机器学习模型构建数据预测模型已成为了各个领域研究的热点。浙江省位于我国沿海地区，每年受极端降雨现象的影响十分严重，造成了浙江省严重的洪涝灾害。为解决这一问题，本文基于高斯回归模型(GEP)、自适应模糊神经网络(ANFIS)、多元自适应回归模型(MARS)和梯度提升决策树算法(GBDT)构建浙江省极端降雨指数预测模型，并将模拟结果与传统机器学习模型进行对比，分析得出最优模型。

1 研究区域与研究方法

1.1 研究区域概况及数据来源

浙江省位于我国东南沿海地区，地处亚热带季风气候区，是中国经济最活跃的省份之一。频繁的台风现象造成了整个浙江省极端降雨的加剧，对全省经济发展造成了严重的影响。本文选择浙江省杭州、慈溪、衢州、丽水等9个气象站点1961—2018年的逐日气象数据，计算不同站点的极端降雨指数。本文数据均通过http://data.cma.cn/网站获取，数据质量控制良好，站点及研究区域概况如图1所示。

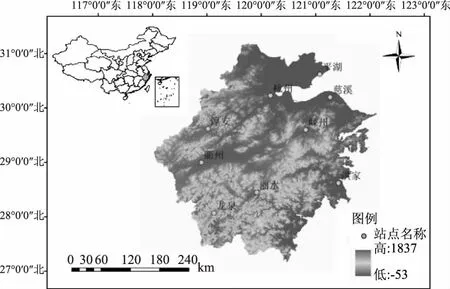
图1 研究区域概况图

1.2 极端降水指数

为构建浙江省极端降雨事件的预测模型，本文选择了世界气象组织气候委员会推荐的3个极端降水指数，分别为每年中雨日数(R10)、大雨日数(R20)和1日最大降水量(RX1)，指标具体含义见表1。

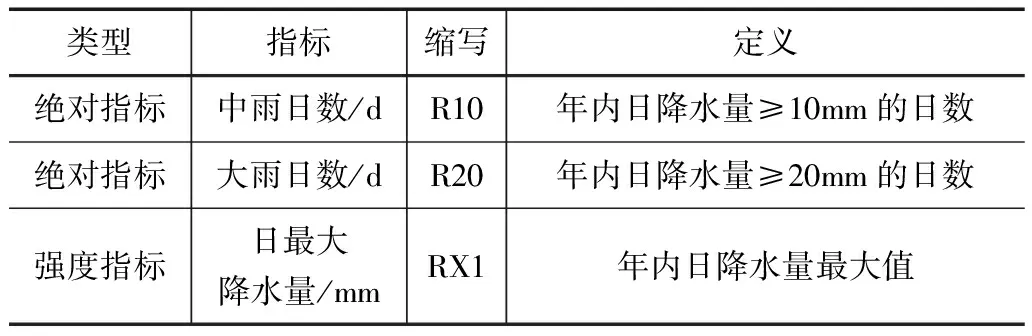
表1 极端降水指数含义表

1.3 几种模型算法

1.3.1高斯回归模型

高斯回归模型(GEP)给定训练集D={(xi，yi)|i=1，2，…n}，其中x为D维输入向量，y为输出的标量，n为训练样本数，输入矩阵X为D×n列的向量，Y为目标输出，因此记为D=(X，Y)，具体步骤可见文献[9]。

1.3.2自适应模糊神经网络

自适应神经模糊神经网络模型(ANFIS)将模糊评价与神经网络模型思想结合起来，采用最小二乘法和反向传播算法进行训练模型和参数调优，在训练过程中自动生成输出结果，具体步骤可见文献[10]。

1.3.3多元自适应回归模型

多元自适应回归模型(MARS)能够在不给出假定约束条件的前提下确定变量之间的关系，对输出变量与输入变量进行非线性建模，其主要优点可估计模型基函数的贡献值，从而允许预测变量的加性和交互影响来确定相应变量[11]。

1.3.4梯度提升决策树算法

梯度提升决策树算法(GBDT)是一种迭代决策树算法，该算法通过对训练数据集中弱学习器的计算，得出每个样本序列的残差，在基于残差训练回归树模型，并且根据回归树的权重更新得出新的模型，最终获取预测结果，具体步骤可见文献[12]。

1.3.5传统机器学习模型

为进一步比较不同模型的精度，得出最优模型，本文选择了4种传统机器学习模型作为对比，分别为极端梯度提升模型(XGBoost)、极限学习机(ELM)、广义回归神经网络(GRNN)和M5回归树(M5T)模型，模型具体步骤可见文献[13]。

1.4 模型精度指标计算

分别以相对均方根误差(RRMSE)、决定系数(R2)、纳什系数(NS)为模型误差评价体系，具体公式如下：

(1)

(2)

(3)

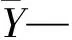
GPI指数可整合3个指标的综合评价结果[14]，公式如下：

(4)

式中，αj—常数，RRMSE取1，NS和R2取-1；gj—不同指标的缩放值的中位数；yij—不同指标的尺度值。

2 结果与分析

2.1 极端降雨指数变化趋势

浙江省3种极端降雨指数的空间变化趋势如图2所示。由图中可以看出，3种极端降雨指数在整个区域均有明显的空间分布规律。R10指数在整个浙江省呈现了由东北至西南逐渐增加的趋势，在衢州附近的R10取值较高，多年平均R10达到了52d，而在平湖附件R10取值最低，多年平均仅为39d；在全省R20的分布规律与R10基本一致，在衢州附近，R20达到了最大值为27d，在平湖附近的R20相对较小，多年平均日降水量超过20mm的天数仅为18d；浙江省RX1呈现出了由西北至东南逐渐升高的趋势，RX1在洪家附近出现最高值，多年平均年内日降水量最大值为142.4mm。

2.2 不同模型R10模拟结果

不同模型对浙江省不同站点R10模拟结果精度对比如图3所示。由图中可以看出，不同模型模拟R10精度有所差异，其中GEP模型在不同站点均表现出了较高的精度，GEP模型的R2、RRMSE和NS中位数分别达到了0.893、3.029%和0.887，该模型GPI达到了1.008，在所有模型中排名第1。MARS模型、ANFIS模型和GBDT模型GPI分别为0.807、0.656和0.563，排名2～4位。传统机器学习模型的精度较低，其中M5T模型的精度最低，其R2、RRMSE和NS中位数分别仅为0.753、6.335%和0.686，GPI仅为-0.257，排名最低。

2.3 不同模型R20模拟结果

不同模型对浙江省不同站点R20模拟结果精度对比如图4所示。由图中可以看出，GEP模型在所有模型中精度最高，其次为MARS模型，2种模型的R2、RRMSE和NS中位数分别达到了0.958和0.950、1.084%和1.751%、0.943和0.839，2种模型的GPI分别为2.585和1.968，在所有模型中排名前2位。ANFIS模型和GBDT模型的精度次之，2种模型的GPI分别为1.858和1.194。在传统机器学习模型中，XGBoost模型和ELM模型的精度高于GRNN模型和M5T模型，M5T模型精度最低，其R2、RRMSE和NS中位数仅为0.805、3.887%和0.545，GPI仅为-0.029。

2.4 不同模型RX1模拟结果

不同模型对浙江省不同站点RX1模拟结果精度对比如图5所示。由图中可以看出，不同模型对RX1的模拟精度与其余2个极端降雨指数基本一致，均表现为GEP模型的精度最高，该模型在模拟RX1时的R2、RRMSE和NS中位数分别为0.929、0.383%和0.950，GPI达到了2.996。所有模型中，GRNN模型和M5T模型精度较低，2种模型的R2、RRMSE和NS中位数仅为0.786和0.771、1.384%和1.551%、0.811和0.765。

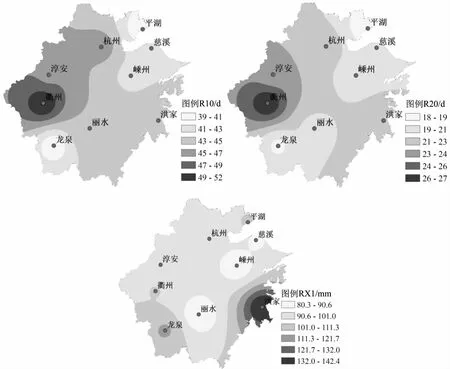
图2 浙江省极端降雨指数空间变化趋势

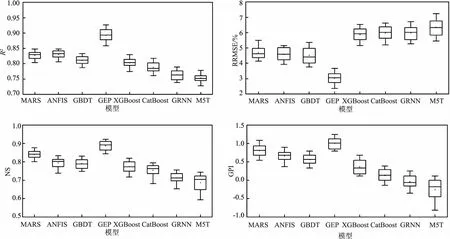
图3 不同模型R10精度对比

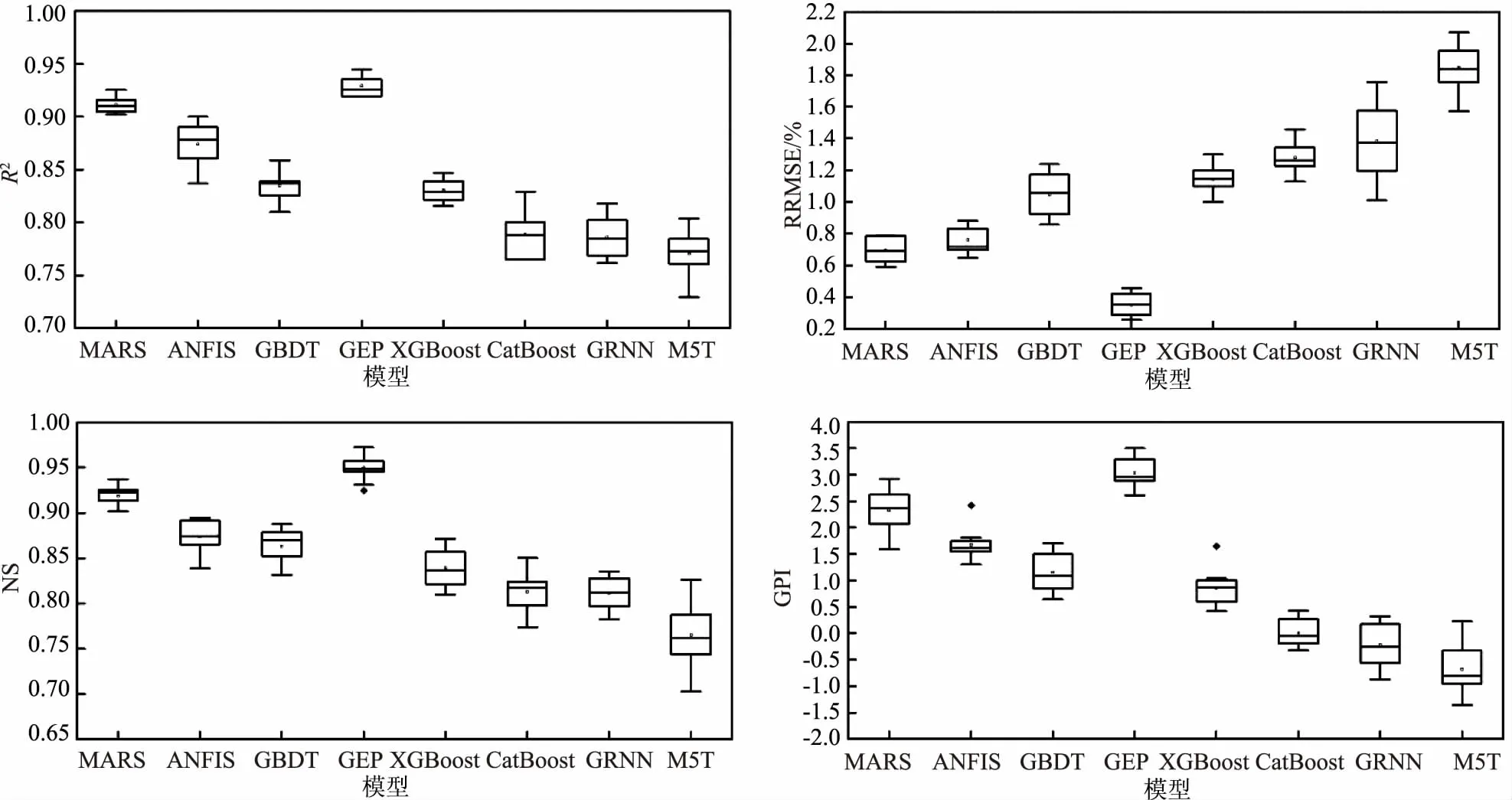
图4 不同模型R20精度对比

综上所述，GEP模型在模拟R10、R20和RX1模拟中的精度较高，GPI在所有模型中均排名第1位，可作为浙江省极端降雨指数预测的标准模型使用。

2.5 极端降雨指数可移植性分析

为进一步证明GEP模型的精度，本文对GEP模型在浙江省极端降雨指数预测的可移植性进行了分析。在全省的9个站点中随机选取3个作为预测组，再随机选取3组(每组3个站点)作为训练组，将训练组的资料进行打乱重分配，构建9组GEP预测模型，对R10、R20和RX1的模拟精度见表3—5。由表中可以看出，对不同指数的模拟精度，GEP模型NS均在0.910以上，R2均在0.932以上，RRMSE均在0.7%～2.8%之间，模拟精度较高，这表明GEP模型在气候条件相似的地区内具有极高的适用性，其预报能力高且稳定，可作为浙江省极端降雨指数的标准模型使用。

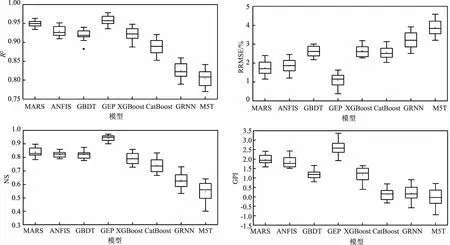
图5 不同模型RX1精度对比

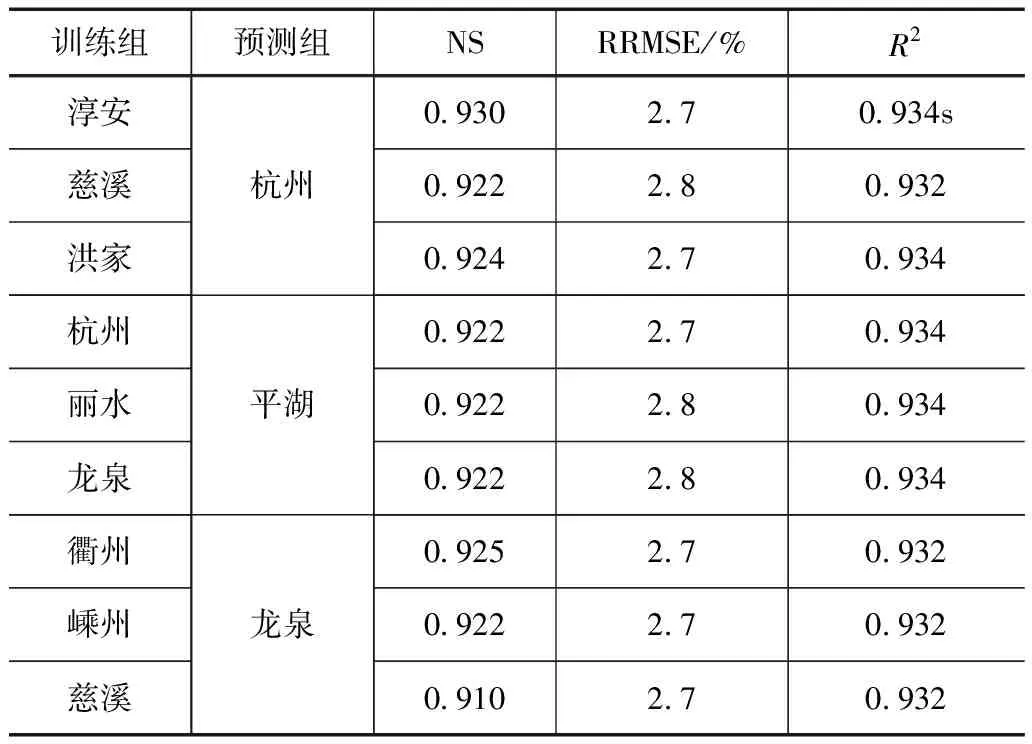
表2 R10可移植性分析结果

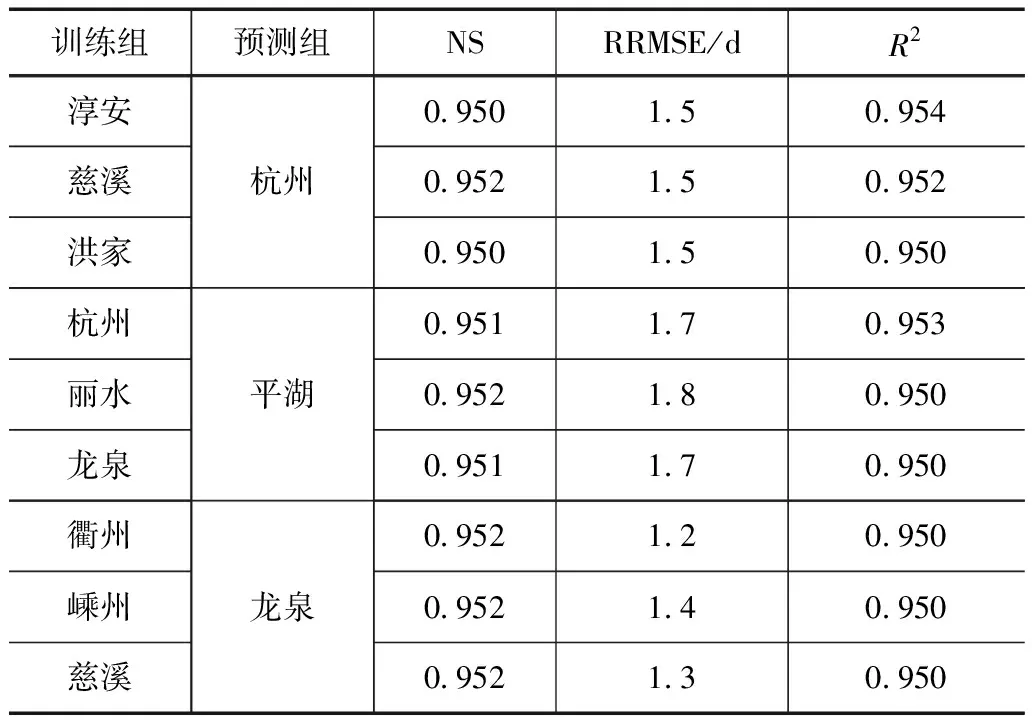
表3 R20可移植性分析结果

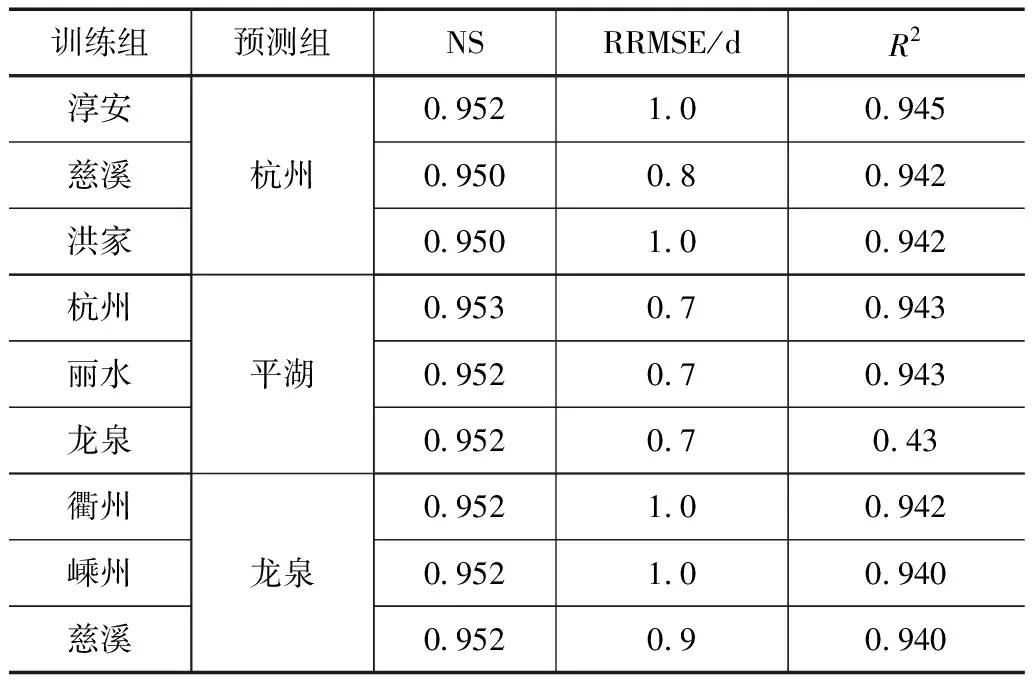
表4 RX1可移植性分析结果

3 结语

本文构建了浙江省不同气象站点的极端降雨指数预测模型，得出以下结论。

(1)通过分析比较不同模型的模拟精度可知，GEP模型在所有模型中的精度最高，在R10、R20、RX1模拟中的GPI均排名第1位。

(2)对GEP模型可移植性进行分析，可知GEP模型在不同训练、预测组合下均能保证极端降雨指数预测的精度，因此，该模型可作为浙江省极端降雨指数预测的标准模型使用。

(3)粒子群算法可显著提高机器学习模型精度，在今后的研究中，可综合比较基于粒子群算法优化的GEP模型和传统GEP模型的精度，进一步提高浙江省极端降雨的预测精度。