基于PSO算法的复杂曲面计量精度补偿方法

王春泉，任华卫(烟台市标准计量检验检测中心，山东 烟台 264003)

0 引言

随着现如今智能化技术的不断成熟与完善，我国多目标、多结构的计量精度技术被应用在社会中的各个领域以及行业之中，取得了相对较好的成果。不仅如此，计量精度技术的提升一定程度上增强了生产的质量和效率，当企业在日常制造以及生产的过程中，利用智能化计量技术，取代传统的人工计量测算，不仅可以缩短计算的时间，扩展测定运算的范围，同时还能够极大地降低测算中产生的误差，使智能化计量改革的进程不断深入[1]。最近几年，智能化计量以及测算等相关技术被广泛应用在复杂曲面的测定计量工作之上，并实现了较大的突破与创新，使我国相关领域经济的发展得到了更大的提升[2]。

复杂曲面的计量是一件十分烦琐且困难的工作，主要是因为，在测量和计算的过程中，由于模型大多为无法平整计量的曲面，所以并没有较为精准的参照物，致使最终测量结果的精准度无法保证，可信性也受到了一定的影响[3]。面对这种情况，再结合实际的应用需求，需要在传统的计量方法之中设立相对应的补偿方法。计量精度的补偿实际上是在测算误差较小的情况下，也就是测定计算结果在合理的范围之中时，对异常区域进行预估数值补偿的一种计量方法，计量精度的补偿方法多被应用在复杂曲面的测定工作之中，与其他补偿方法相比，可以更好地缩小曲面计量的误差值，结合智能化计量模式实现更好的补偿效果[4]。

PSO算法是一种多方向、多目标的应用型应变距离补偿算法，它的应用一般是具有较大限制性的，对于计量环境的要求极高，同时补偿范围也相对较大，对于简单的曲面计量精度的补偿，结果十分有限，并且具有较低的稳定性；反之，如果被应用在复杂的曲面计量工作之中，自身巨大的补偿范围会缩小曲面之间的精度误差，同时形成更加完整的曲面补偿模型，依据初始的计量结构，结合模型的实际曲面面积，最终可以得出更加精准的补偿结果[5]。因此，对基于PSO算法的复杂曲面计量精度补偿方法进行设计与研究。本文在较为真实的环境之下，创建补偿模型，同时建立复杂曲面的计算测量方法，利用PSO算法计算出对应的补偿范围，将两个范围进行重合，重叠在一起的部分测试预估的补偿范围，计算补偿精度值，完成方法的设计，同时提高整体的智能计量补偿水平。

1 PSO算法下复杂曲面计量精度补偿方法设计

1.1 复杂曲面补偿螺距确定

在进行PSO算法下复杂曲面计量精度补偿方法的设计之前，需要对复杂曲面补偿螺距进行确定。通常情况下，螺距的控制与补偿的实际范围存在一定的联系，而产生相对应的补偿误差包括以下两种，分别为反向螺距间隙误差补偿与螺距误差补偿，这两种补偿误差之间的作用效果是双向的，并且定位的精度值也具有一定的限制，具体的限制补偿极限差值计算如下公式(1)所示：

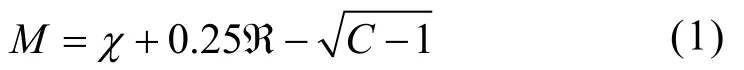
式中：M为限制补偿极限差值；χ为精度补偿偏差；ℜ为双向作用距离；C为反向间隙值。

通过上述计算，最终可以得出实际的限制补偿极限差值。将其设定为补偿的误差标准，同时依据实际的需求，设立计量精度目标，在复杂曲面的环境之下，设定的双向补偿距离以及螺距误差补偿范围通常是一致的，但需要注意的是，螺距误差补偿范围是针对于曲面的侧向数值的计量的，精准度相对较高，同时具有一定的可修改性[6]。设定中控补偿距离，并进行复杂曲面实际补偿螺距的计算，如下公式(2)所示：

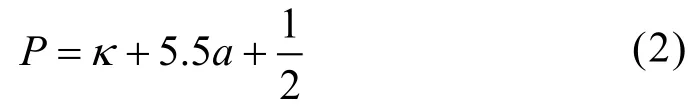
式中：P为复杂曲面实际补偿螺距；κ为补偿间隙值；a为反向均值。

通过上述计算，最终可以得出实际的复杂曲面实际补偿螺距。将其设定在计量补偿结构之中，为后续的计算奠定基础。

1.2 PSO算法下QR分解补偿阶次建立

在完成对复杂曲面补偿螺距的确定之后，接下来，需要在PSO算法下进行QR分解补偿阶次的建立。QR分解补偿阶次指的是在计量精度补偿过程中，将复杂曲面预估补偿区域进行层次测定核算分解，进行阶段式的计算[7]。在对曲面实际情况辨识之前，设定不同的分解阶段，每一个阶段均为独立计算的，同时均具有对应的QR补偿值[8]。在输入测定信号后，将补偿范围设定为0～200，实际的补偿误差设定为6[9]。为了获取到更好的补偿效果，将数值设定在QR分解补偿阶次之中，结合PSO算法设立计量精度补偿矩阵，具体如下公式(3)～(5)所示：

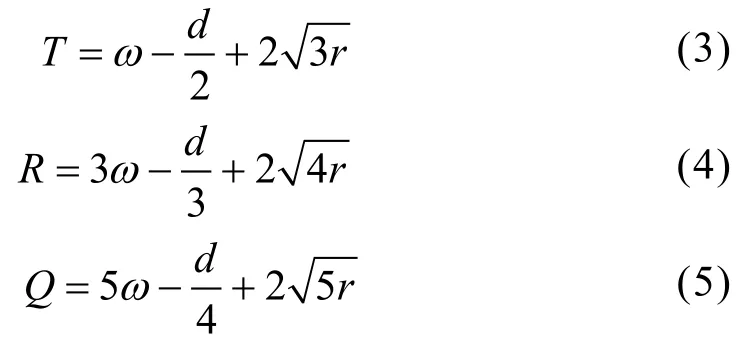
式(3)～(5)中：T、R、Q分别为分解补偿阶次范围值；ω为谐振距离；d为高阶次指数；r为辨识系数。

通过上述计算，最终可以得出实际的分解补偿阶次范围值。将其设定在不同的阶次之中，完成PSO算法下QR分解补偿阶次的最终建立。

1.3 PSO算法对偶迭代补偿模型创建

在完成PSO算法下QR分解补偿阶次的建立之后，接下来，需要进行对偶迭代模型的创建。其实，PSO算法实际上是一种改进粒子群计算方法，对比于传统的算法，具有更大的优势，对于庞大数据的处理效果更好。在PSO算法的基础之上，进行对偶迭代次数的引导设定。完成之后，将设定的标准添加在QR分解补偿阶次之中，形成独立的对偶迭代补偿模型。模型中需加置PSO算法对复杂曲面的多项数值进行测定与分析，在不同的情况之下，进行曲面的测算与核定，进一步完善优化PSO算法对偶迭代补偿模型的应用效果。

1.4 归一特征控制实现PSO算法下的计量补偿

在完成PSO算法下对偶迭代补偿模型的创建后，接下来，需要加强归一特征的控制来最终实现PSO算法下的计量补偿。依据实际复杂曲面的计量特征，设立不同的补偿目标，将补偿目标添加在对偶迭代补偿模型之中，利用模型的分化性质提取出复杂曲面自身具有的计量特征，对提取的特征进行归一化处理，并计算出动态特征补偿幅值，如下公式(6)所示：

式中：F为动态特征补偿幅值；n为变化补偿比；ν为重叠曲面补偿范围。

通过上述计算，最终可以得出实际的动态特征补偿幅值。依据数值对复杂曲面的计量精度作归一化处理，测算出最终的补偿数值，实现PSO算法下复杂曲面计量精度的补偿。

2 方法测试

本次测试主要是对PSO算法下复杂曲面计量精度补偿效果的测试与验证。测试共分为两组，一组为传统的激光补偿精度补偿法，将其设定为传统激光精度补偿测试组；另一组为本文所设计的计量精度补偿方法，将其设定为PSO算法精度补偿测试组。在相同的测试环境之下，对两组方法同时进行测试，测试所得出数据信息进行对比分析，最终完成对测试目标的计量与补偿。

2.1 测试准备

在测试前，需要先进行对应的测试准备。在基础复杂曲面物面倾角与感光器件倾角的双向作用基础之上，创建对应的补偿偏差标准，完成对复杂曲面物面倾角与感光器件倾角补偿偏差标准的设定。完成之后，在基于标准补偿差值之上，结合Matlab软件进行补偿测试模型的创建，同时，依据上述的标准，进行补偿规则以及机制的设立，与此同时，还需要建立对应的曲面计量精度补偿结构，此项结构包括对激光传感器模块的建立、双向位移坐标测量模块的关联、目标曲面以及物面实际面积的设定以及补偿极限值的明确等。

随后根据所设定的补偿范围，进行关联精度计量补偿系数的计算，具体如下公式(7)所示：

式中：K为关联精度计量补偿系数；β为预估补偿范围；f为应变系数；ℑ为允许出现的极限补偿误差。

通过上述计算，最终可以得出实际的关联精度计量补偿系数。将其划归至测试补偿模型之中，同时设定关联补偿标准。另外，依据复杂曲面的测验补偿范围，进一步完善对应的测试模型。根据设定的对应标准，在实际需求的补偿需求的引导之下，进行复杂情况下，对应的计量数值的更改与调整。至此便完成相关的测试准备，核查测试所应用的设备以及装置是否处于稳定的运行状态，同时确保不存在影响最终测试结果的外部因素，核查无误后，开始测试。

2.2 测试过程及结果分析

在上述所搭建的测试环境之中，进行具体的复杂曲面计量精度补偿测试的实施。选取的曲面数值采集汇总，同时，添加在模型之中，测算出对应的初始补偿结果之后，根据实际补偿需求，在复杂且不同的曲面环境下，创建补偿重叠矩阵，同时进行不同静曲面的计量，利用PSO算法，结合补偿重叠矩阵，建立二次补偿结构。并通过对比得出实际的补偿偏差。依照上述计算，最终可以得出对应的测试结果，进行对比分析，如表1所示。

根据表1中的数据信息，最终可以得出实际的测试结果：在不同的复杂曲面补偿量程范围之下，对比于传统的激光精度补偿测试组，本文所设计的PSO算法精度补偿测试组最终得出的补偿偏差相对较低，这表明应变补偿的范围有所变化，计量精度的补偿误差有了明显的降低，使得补偿效果更佳，具有实际的应用价值。

表1 测试结果对比分析表

3 结语

综上所述，便是对基于PSO算法的复杂曲面计量精度补偿方法的设计与研究。对比于传统的补偿方法，本文所设计的PSO算法下的计量精度补偿方法具有更强的灵活性，在应用的过程中，对于复杂曲面误差区域的处理以及核算均较为灵活，可以在补偿模型之中，将产生的误差最大限度地降至最低。不仅如此，由于曲面的复杂性在计量的过程中更极容易出现倾角偏差。但是利用PSO算法可以实现倾角偏差的循环补偿，不仅缩短了核算的时间，同时形成的夹角也不会对补偿模型造成任何的影响，根据所设定的补偿模型分别估算出计量偏差值以及补偿偏差值，形成归一化的补偿关系，以此来进一步实现精度偏差的对应补偿提升补偿方法的准确性，加强补偿的实际效果。