基于双向流固耦合的超空泡射弹入水研究1)

郝常乐 党建军 陈长盛 黄 闯,2)

* (西北工业大学航海学院,西安 710072)

† (上海船舶设备研究所,上海 200031)

引言

超空泡射弹是一种动能武器,依托火炮从空中发射入水,借助超空泡减阻技术能够在水下高速长距离航行,是对抗鱼雷、水雷和蛙人等小型水下威胁的有效手段.为了扩大防御范围、增加杀伤力,超空泡射弹应拥有更高的发射速度[1].

超空泡射弹的初始速度主要取决于发射装置,当前火炮的射速能够达到1.7 km/s[2],电磁炮的射速可达2.5 km/s[3-4].提高初始速度是增加射弹动能的有效途径,然而也使得射弹在入水过程中受到的载荷按平方关系增大[5].高速条件下,因入水冲击产生的应力有可能超过射弹材料的屈服极限,引起结构破坏[6],是造成射弹弹道失稳的主要原因,引起了国内外的重视[7].

Hrubes[8]在美国水下作战中心开展了射弹入水实验,发现设计不合理的射弹在高速入水时会发生塑性弯曲变形,并引发弹道失稳.Chen 等[9]对超空泡射弹的垂直入水问题开展了试验研究,发现在有初始攻角条件下,随着射弹初速度的提高,射弹的入水运动稳定性显著降低.周杰和徐胜利[10]、胡明勇等[11]分别使用光滑粒子流体动力学(SPH)方法和任意拉格朗日欧拉(ALE)方法研究了高速平头射弹垂直入水过程中的结构失效问题,发现高速条件下射弹的空化器边缘会因应力集中而产生塑性变形,甚至结构破坏,但是都忽略了自然空化问题.梁景奇等[12]采用数值仿真的方法,研究了高速射弹入水攻角对空泡形态及流体动力特性的影响,指出入水攻角通过改变射弹的沾湿状态影响入水冲击载荷.陈晨[13]考虑了水、空气、水蒸气三相的可压缩性,对射弹跨音速入水问题进行了仿真研究,发现射弹的入水空泡内主要是水蒸气相,在入水的短暂过程中流体的压缩性对空泡形态的影响可忽略.黄闯[14]对超空泡射弹入水弹道特性进行了仿真研究,发现在入水2 倍弹长后的空泡流型特性和射弹流体动力特性与水下定常工况无显著差异.Kim 等[15]发现空化器攻角对超空泡的发展过程和稳定形态有显著影响.Akbari 等[16]对高速超空泡射弹斜射入水问题进行了试验和仿真研究,发现射弹的侧面受到了较大的冲击载荷,该载荷取决于射弹的沾湿状态.

公开文献显示,超空泡射弹在高速入水时会受到巨大的冲击载荷,进而引发显著的结构变形.结构变形条件下,超空泡射弹的流体动力载荷特性必然发生变化.因此,高速射弹在入水过程中存在结构与流动强耦合问题.常用于解决流固双向耦合问题的SPH 方法和ALE 方法在对多相流动、相间质量传递等问题时存在不足[17-18].基于有限元(FEM)和有限体积(FVM)的分区求解法,使用成熟的FVM 求解器和FEM 求解器分别计算流场和结构,能够解决超空化流动、复杂变形、流固双向耦合等问题[19-21],非常适合用于求解高速超空泡射弹入水过程中的空泡流型、冲击载荷和结构变形问题.

为了解决超空泡射弹高速入水过程中的流固耦合问题,本文首先基于Fluent 16.0和Abaqus 6.14 求解器之间的实时交错迭代,建立了一种能够同时计算超空化流动、入水冲击载荷、弹性变形、塑性应变等复杂流动和结构问题的双向流固耦合计算模型.然后,对初速1400 m/s 的超空泡射弹在不同攻角垂直入水过程的流固耦合问题进行了仿真计算,获得了高速射弹在入水过程中的空泡流型、流体动力载荷特性以及射弹结构变形特性,以期为超空泡射弹设计和运用提供参考.

1 模型的建立

1.1 控制方程

超空泡射弹的入水流场包含空气、液态水、水蒸汽三相流动,且液态水和水蒸气之间存在质量传递,有清晰的相间界面.VOF 模型属于单流体模型,适用于有清晰界面的多相流动,在超空泡流动的数值仿真计算中应用广泛[12,19,22].超空化流动与结构变形双向流固耦合数值模型的控制方程主要包括连续性方程、动量方程、空化模型和材料本构方程等.

(1)连续性方程

其中,ρm为多相流混合密度,vm为多相流的质量平均速度,ρk和αk分别为第k相的密度和体积分数,nphase为多相流的相数,对于本文研究的情况nphase=3 .

(2)动量方程

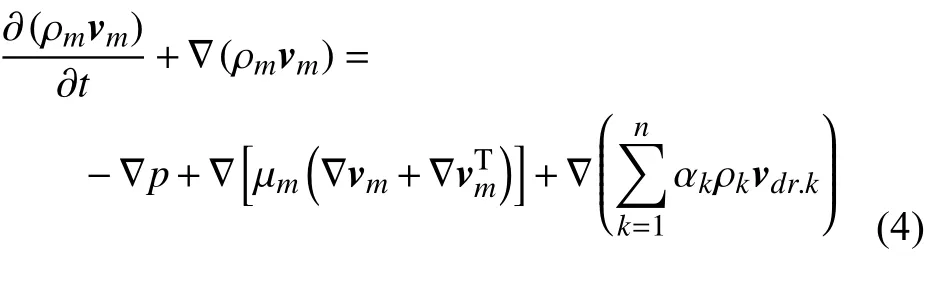
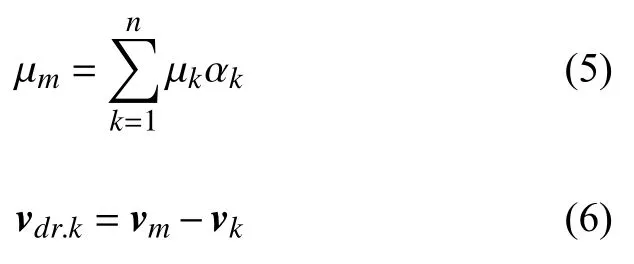
其中,p为压力,μk为第k相的动力黏度,μm为多相流混合动力黏度,vk为第k相的速度,vdr.k为第k相与主相的相对速度表达式,S为源相.

(3)空化模型

超空泡射弹的速度高,周围的局部压力会低于水的饱和蒸汽压,存在自然空化现象.因此,需要引入空化模型模拟液态水与水蒸气之间传质过程.Schnerr和Sauer 空化模型[23]描述了气液混合物中小气泡直径、数量与相间质量传递速率的关系

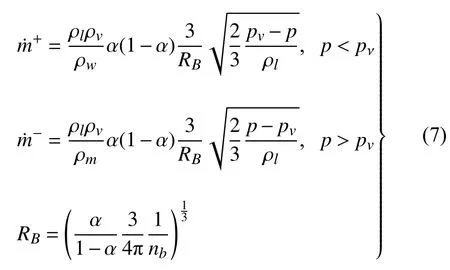
其中,为蒸发率,为凝结率,RB为空泡半径,nb为单位体积空泡数,计算中取nb=1×1013.

此外,本文使用的湍流模型为Realizablek-ε模型,壁面函数为尺度化壁面函数,使用SIMPLE 算法求解控制方程.

(4)材料本构方程

入水射弹的结构变形是一个瞬间大应变率过程,材料的应力应变特性具有强烈的时变性和非线性.以钨合金为例的材料应力应变特性可使用Johnson-Cook 本构方程[24-25]进行描述,具体如下

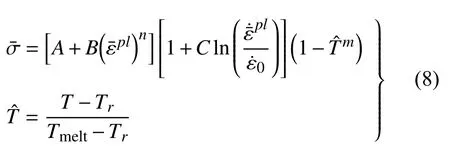
其中,Tmelt为材料熔点.参数A,B,C,m,n为常数,由实验测得,A为准静态下屈服应力,B为应变硬化常数,C为应变率相关系数,m为温度相关系数,n为应变硬化指数.以93 钨合金材料[26]为例,相关物性参数见表1.

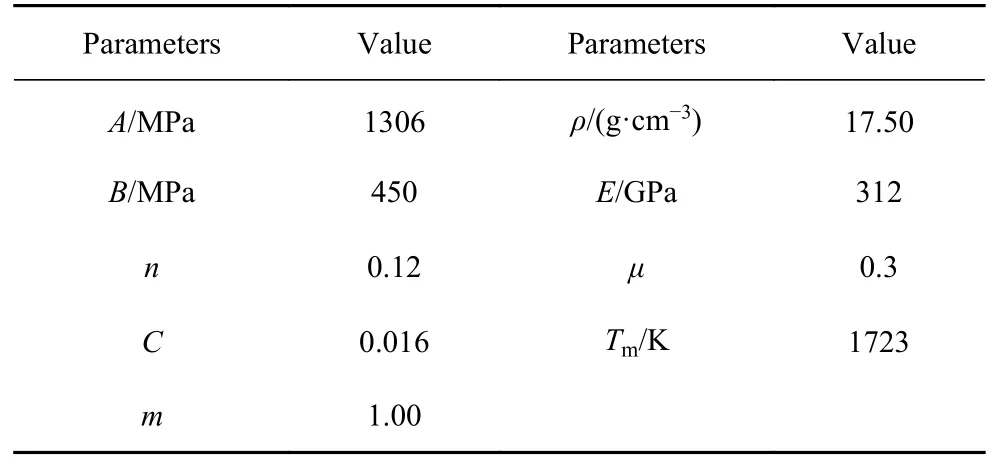
表193 钨合金材料性能参数Table 1 Performance parameters of tungsten alloys 93

1.2 研究对象及网格划分

以图1 所示的超空泡射弹为例,研究其在不同攻角垂直入水过程中的多相流动和结构变形问题.射弹由2 个锥段和1 个柱段构成,材料为93 钨合金,采用圆盘空化器,主要外形参数如图1(a)所示.

为准确模拟射弹入水时相对于自由液面的运动状态以及远场空泡的发展过程,设计了圆柱体计算域,如图1(b)所示.根据前人的研究结论[14],在确保计算结果不受影响的前提下确定了计算域的大小:直径为400 倍空化器直径,长度为11 倍弹长.

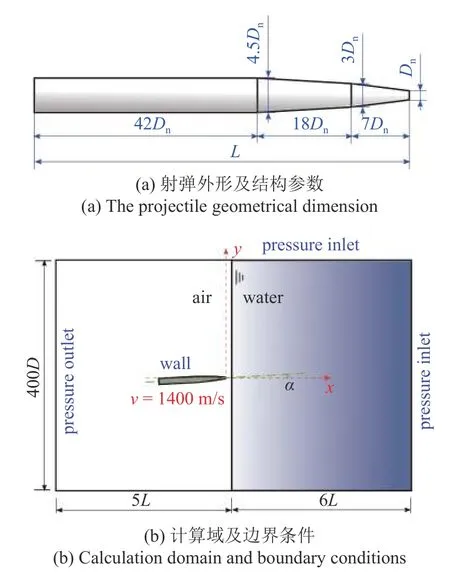
图1 几何尺寸及边界条件Fig.1 Geometries and boundary conditions

为了获得高速射弹在入水过程中的空泡流型和结构变形特性,以初速为1400 m/s 的超空泡射弹为例,在垂直入水初始攻角α分别为0°,2°,4°,6°和8°的条件下开展仿真计算.

射弹入水速度高,入水过程中的位移大,采用运动参考系方法可有效提高网格重构效率.计算域入口边界条件为压力入口,表压为0 Pa.射弹表面为无滑移壁面,同时也是流固耦合的耦合面.参考系以1400 m/s 的速度向x轴正向运动.

流固耦合仿真的计算域包括流体域和固体域,对结构和流体域分别划分网格,网格划分结构如图2所示.固体域网格单元为8 节点六面体线性减缩积分单元;流体网格为六面体网格,为了获得准确的空泡外形,对流场中体积分数梯度、压力梯度和速度梯度较大的区域进行网格加密,主要网格加密的区域包括:空化器附近、弹体附近空泡区域和两相交界区域.经验证,固体域网格单元数为76 000、流体域网格单元数为470 000 的计算域划分结果满足网格无关性要求.

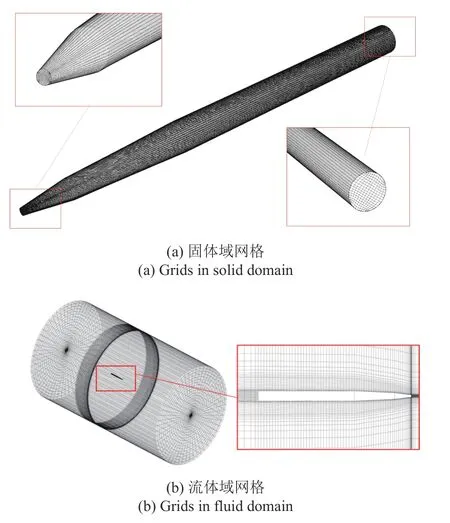
图2 计算域网格划分情况Fig.2 Grids of fluid and solid domains

1.3 耦合方法

在超空泡射弹入水过程中,射弹结构受到的载荷取决于泡体的相对位置,载荷引起的结构变形又改变射弹的泡体相对位置,射弹结构的变形和流体动力之间存在耦合关系.为计算射弹结构变形和流场之间的耦合效应,需要在计算流体力学求解器(CFD 求解器)和计算固体力学求解器(CSD 求解器)之间建立数据双向实时传递通道[27].本文分别对Fluent 16.0和Abaqus 6.14 进行二次开发,基于MpCCI 建立了二者之间的数据传递和交错迭代,实现了双向流固耦合仿真计算[28].

流固耦合仿真分析的求解过程如图3 所示.CFD 求解器和CSD 求解器分别用于计算流体模型和结构模型,CFD 求解器计算得到作用在耦合面上的流体动力,经过映射作为载荷输入到CSD 求解器中耦合面上.CSD 求解器根据输入的载荷计算结构的结构响应,并将耦合面上的节点位移经过插值映射到CFD 求解器对应的耦合面上,对CFD 求解器中耦合面进行变形.CFD 求解器通过动网格方法对变形后的网格进行光顺和重构,使其能满足CFD 仿真计算的要求,至此完成一个耦合步的数据交换与计算.将整个流固耦合过程划分为若干个耦合步的计算,达到计算停止条件后终止耦合计算.

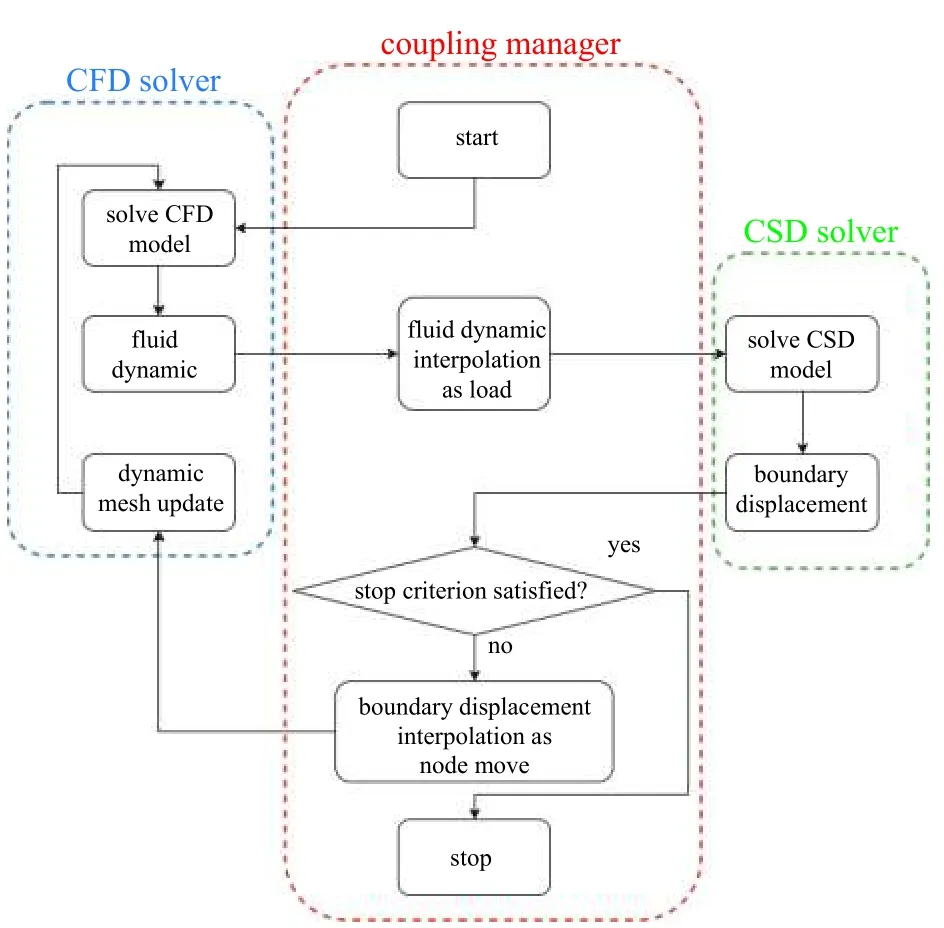
图3 双向流固耦合计算流程图Fig.3 Flowchart of bidirectional fluid structure interaction

2 模型验证

分别采用经典文献中关于入水空泡流型特性和流固耦合变形特性的研究结果,验证第1 节中流固耦合仿真模型的准确性.

2.1 空泡形态计算方法验证

哈尔滨工业大学的郭子涛等[29-30]对平头弹在高速垂直入水的空泡发展开展试验研究得到的平头弹入水后的空泡外形.试验模型为φ12.35 mm ×25.4 mm 圆柱,通过轻气炮发射垂直入水,入水初始速度为603 m/s.

使用对试验工况开展仿真计算,获得了入水相同时间后的空泡外形.仿真结果与文献的试验结果对比如图4 所示.空泡截面直径的最大相对偏差为6.53%,表明第1 节中建立的数值模型对于超空泡流动问题具有较高的计算精度.

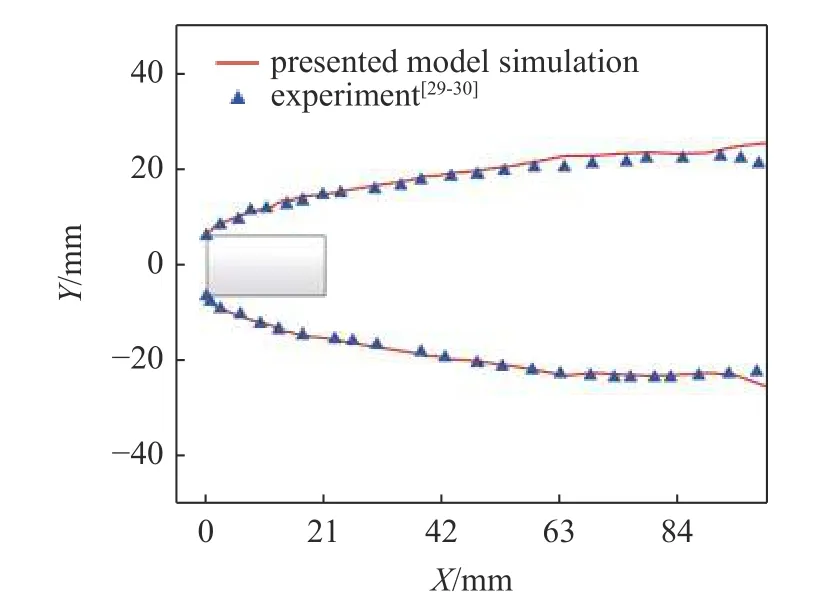
图4 入水空泡外形的仿真与试验结果对比Fig.4 Comparison of simulation and experiment results of supercavity

2.2 流固耦合方法验证

Walhorn 等[31]通过研究弹性薄板在涡街中的振动问题,提出了一种验证流固耦合的方法.边长为1 m 的正方形刚体在速度为51.3 m/s 的来流中产生涡街,长方形后方的弹性薄板长4 m、厚0.6 m,在涡街的驱动下发生振动.

使用分离求解双向流固耦合模型对文献工况进行计算,得到弹性薄板自由端位移如图5 所示.文献计算结果振动周期0.33 s,平均振幅1.01;使用双向流固耦合模型计算得到的振动周期0.31 s,相对偏差为6%,平均振幅0.97,相对偏差4%,与文献结果的偏差较小,表明分离求解双向流固耦合模型的仿真精度较高,可以适用于复杂流场中大变形流固耦合问题的仿真计算.

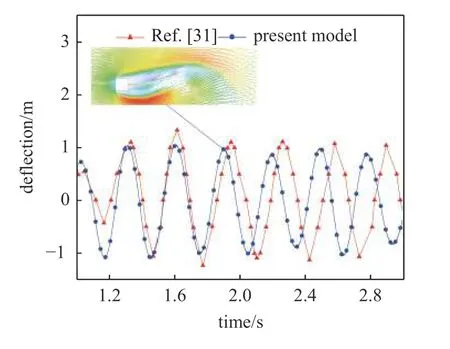
图5 弹性薄板自由端挠度仿真与文献结果对比Fig.5 Comparison of calculated deflection of free end point of elastic plate and literature result

3 超空泡射弹高速入水流固耦合数值研究

以初速1400 m/s 的超空泡射弹的垂直入水工况为例,通过流固耦合仿真,研究不同初始攻角入水过程中的空泡流型、流体动力载荷和结构响应特性.为了分析流固耦合效应对结构变形和超空泡流动的影响,还计算了刚性射弹的超空化流场.

3.1 入水空泡流型特性

在初始攻角为0°～ 8°范围内开展双向流固耦合仿真,攻角取值间隔为2°,得到不同初始攻角条件下,射弹附近流场的演变过程.以初始攻角为0°,4°和8°为例,入水2 倍空化器直径、入水1 倍弹长和入水2 倍弹长对应的流场纵剖面液相分布如图6所示.

图6 初始攻角对射弹结构变形及超空泡流型的影响Fig.6 Influence of initial angle of attack on structure deformation and supercavity

随着攻角的增大,射弹在入水过程中逐渐发生弯曲变形;初始攻角对射弹在入水2 倍弹长的结构变形和空泡流型有显著影响.

为进一步揭示入水攻角对空泡流型的影响,使用刚体假设和流固耦合的方法分别计算射弹入水,提取不同攻角下射弹入水2 倍弹长后的空泡外形进行对比,如图7 所示.

图7 不同攻角入水2 倍弹长后的空泡外形Fig.7 Supercavities of different initial angles of attack when flying 2L underwater

射弹的入水初始攻角为0°和2°时,射弹除空化器外完全被空泡包裹,侧面不出现沾湿区域,射弹没有发生明显的弯曲变形;入水初始攻角为4°,6°和8°时,入水2 倍弹长后,射弹侧面出现大面积的沾湿区域,弯曲变形非常明显.与相同攻角下入水的刚性射弹计算结果对比,发现射弹的结构弯曲变形使得空化器的位置发生偏转,增大了空化器的局部攻角,导致空泡整体沿弹体弯曲方向发生偏移,进一步增大了射弹的沾湿面积.因此,对于高速射弹而言,在大攻角入水过程中的流固耦合效应不可忽略.

3.2 超空泡射弹的流体动力载荷特性

通过仿真计算,获得了考虑流固耦合条件下不同初始攻角入水2 倍弹长后对应的射弹表面压力分布情况,与同等条件下刚性射弹的计算结果进行对比,如图8 所示.

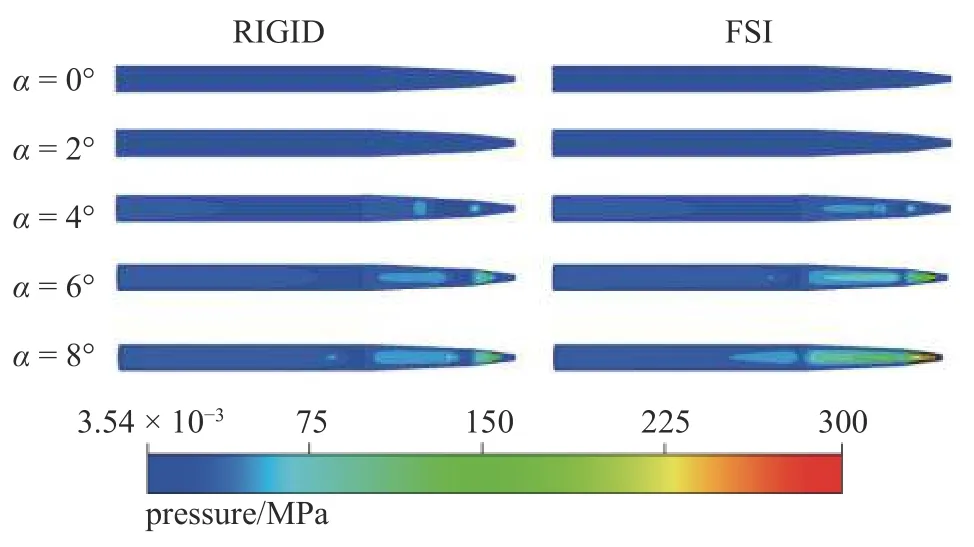
图8 射弹入水2 倍弹长表面压力云图Fig.8 Distributions of pressure on projectiles when flying 2L underwater

综合图7和图8 中流固耦合计算结果与同工况下刚性射弹计算结果的差异,可以得到:弯曲变形增大了射弹的沾湿面积和沾湿区的局部攻角,两方面综合作用使得沾湿区受到流体动力载荷增加,导致射弹的升力和阻力相对于未发生弯曲变形时都有显著的增加.

以水的密度、入水速度、射弹圆柱段截面积为参考值对流体动力进行无量纲化,得到升力系数Cl和阻力系数Cd

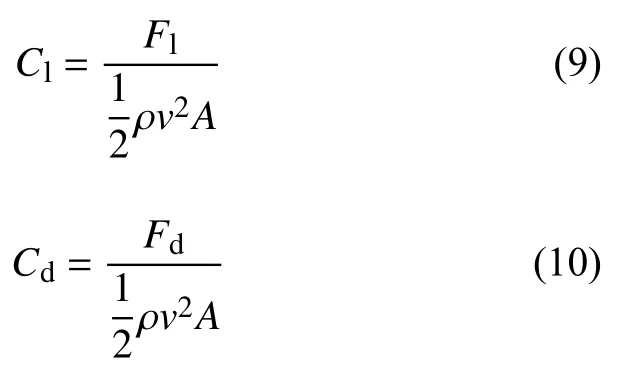
式中Fl=Fl(t),为超空泡射弹入水过程中受到的升力;Fd=Fd(t),为超空泡射弹入水过程中受到的阻力;ρ 为水的密度;A为参考面积;v为参考速度.经过计算,在射弹入水2 倍弹长后,阻力引起的最大速度衰减为5 m/s,仅为初始速度的0.36%,故在计算升阻力系数时均以初速度作为参考速度.

超空泡射弹从刚接触水面到入水2 倍弹长过程的升力系数曲线与阻力系数曲线如图9 所示.当超空泡射弹入水攻角为0°和2°时,射弹的升力系数几乎为0,阻力系数在经过入水冲击的峰值后也很快下降并稳定,此时考虑流固耦合效应的计算结果曲线与刚性射弹计算结果无明显差异;本文所研究的超空泡射弹的入水攻角为4°,6°和8°时,考虑流固耦合效应的射弹在入水的过程中由于沾湿面上受到流体的冲击力导致射弹发生弯曲变形,而射弹的弯曲变形又反过来使射弹的沾湿面积增大,形成一种正反馈,使得作用于射弹的流体动力载荷更大.在这种正反馈的作用下,射弹的升力系数和阻力系数在入水后保持增大.与相同初始攻角入水的刚性射弹的升力曲线与阻力曲线相比,考虑流固耦合效应计算得到的升阻力曲线在入水短时间内与刚性射弹的一致,但到达一定时间后开始快速升高,并且在计算范围内不会到达稳定值.

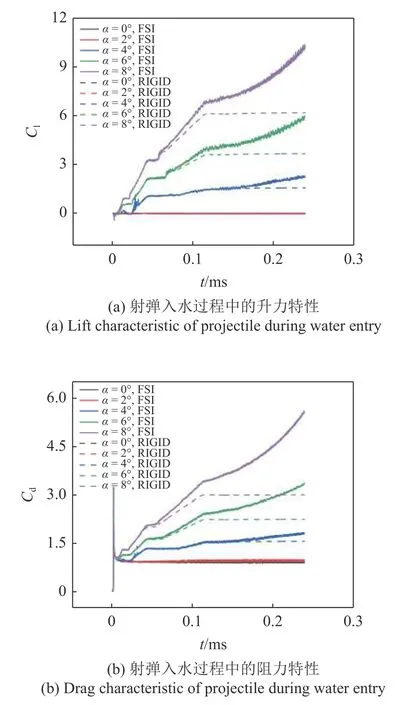
图9 射弹入水过程中的流体动力载荷特性Fig.9 Hydrodynamic characteristics of projectile during water entry

3.3 超空泡射弹的结构变形特性

高速超空泡射弹入水2 倍弹长后等效应力云图如图10 所示.在入水初始攻角较小时(0°和2°),射弹的应力主要由入水冲击及轴向载荷引起,集中在空化器附近.在入水初始攻角较大时(4°,6°和8°),射弹因侧面沾湿受到侧向载荷,在侧面也存在较大的应力分布,射弹侧面的等效应力随入水初始攻角的增加而显著增大.

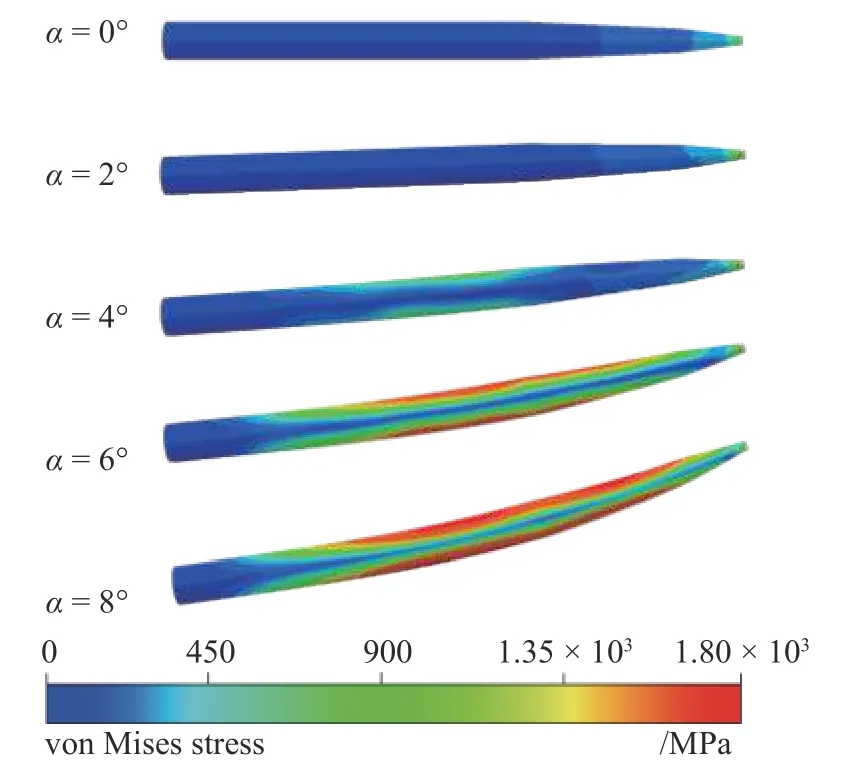
图10 射弹不同攻角入水2 倍弹长后的应力云图Fig.10 Contour of stress after water entry at different angles of attack and twice its length

为了定量表达射弹的结构变形程度,提取轴线上每一点对应的侧向位移.不同入水初始攻角条件下,在入水2 倍弹长时刻的弹轴侧向位移对比结果如图11(a)所示.其中,横轴为归一化的轴向坐标,以射弹头部为零点.超空泡射弹以0°和2°初始攻角入水至2 倍弹长时,射弹主要受到轴向载荷的作用,弹轴几乎没有发生弯曲变形.超空泡射弹以4°,6°和8°初始攻角入水至2 倍弹长时,受到较大的侧向载荷作用,弹轴发生了显著的弯曲变形,入水初始攻角越大,弹轴的侧向位移就越大.

射弹空化器中心点处的挠度-时间曲线如图11(b)所示.超空泡射弹以0°和2°攻角入水时,空化器中心没有出现明显的侧向偏移.超空泡射弹以4°,6°和8°攻角入水时,空化器中心的挠度主要由作用于沾湿区域的侧向力引起的,且随时间的增加逐渐增大.当增加入水初始攻角时,作用于射弹沾湿区域的侧向载荷也增大,使得空化器中心挠度随时间的增长率及末态值都显著增大.

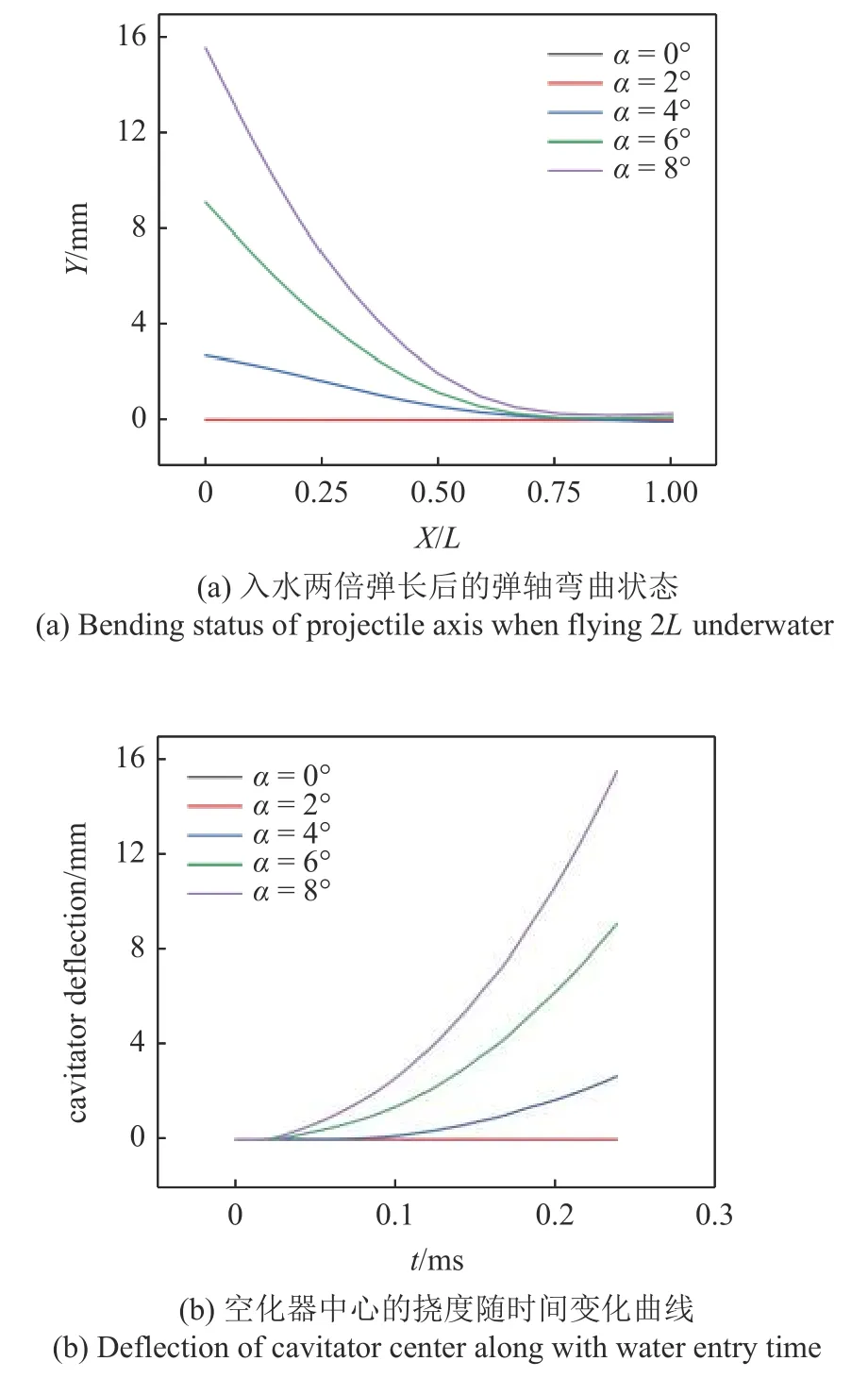
图11 射弹结构参随时间变化曲线Fig.11 Deflection of cavitator center along with water entry time

根据图10 所示,射弹在以6°和8°攻角入水至两倍弹长时,弹体的应力主要集中于第二锥段和圆柱段上,最大值分别为1637 MPa和1895 MPa,已超过钨合金的屈服强度1306 MPa,射弹会发生局部塑性应变.射弹的塑性应变分布情况如图12 所示.初速为1400 m/s 的超空泡射弹,在入水初始攻角为0°～8°范围内,空化器在入水过程中受到巨大入水冲击及轴向载荷作用,会发生显著的塑性变形.由于入水冲击持续时间短,作用面积小,塑性变形仅发生在空化器迎流面附近区域.当入水初始攻角在4°及以下时,射弹侧面没有出现沾湿或者沾湿面积不大,射弹侧面没有发生明显的塑性变形.当入水攻角为6°和8°时,超空泡射弹因大面积沾湿受到很大的侧向载荷,侧面上出现了大面积的塑性应变.

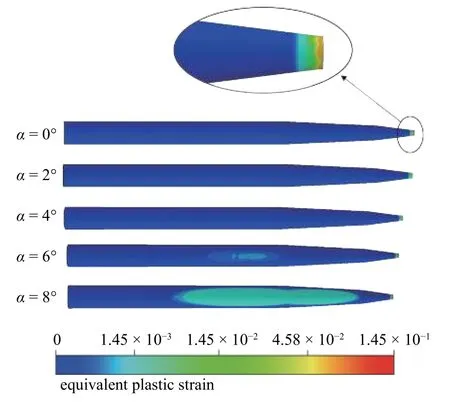
图12 射弹不同攻角入水的等效塑性应变分布Fig.12 Contours of equivalent plastic strain of projectiles with different initial angles of attack

当射弹的结构弯曲发生塑性应变后,射弹原本的设计结构就已经受到了破坏,可以认为射弹失效.以6°和8°攻角入水的射弹在入水2 倍弹长的范围内就已经发生失效;4°攻角入水的射弹在入水2 倍弹长的时间内没有在产生弯曲塑性应变,但是结合图9和图11 中4°攻角入水的曲线来看,在之后的时间内其受力持续增大,结构弯曲变形的挠度也持续增大,在随后的运动过程中也可能会出现塑性变形.入水初始攻角为 0°和2°时,在计算航程范围内,射弹侧面没有沾湿,轴线几乎没有发生弯曲变形,能够安全稳定入水.

4 结论

本文通耦合CFD 求解器和CSD 求解器,建立了超空泡射弹高速入流固耦合数值模型,考虑射弹弯曲变形与空泡流体动力之间的相互影响,研究了高速射弹带攻角入水过程中的超空泡流动及结构变形问题,结论如下.

(1)超空泡射弹在高速大攻角入水条件下,因表面沾湿受到的流体力使弹轴发生了明显的弯曲变形,弯曲变形对超空泡流型及射弹的流体动力载荷均有显著影响,射弹不能当作刚体进行处理.

(2)在研究的工况范围内,所研究的超空泡射弹在侧向载荷作用下发生弯曲变形后,空泡偏离程度及局部攻角的增加进一步增大了射弹受到的流体动力载荷,射弹的流体动力载荷与弯曲变形之间形成正反馈.

(3)所研究的高速超空泡射弹在入水过程中受到的流体动力载荷及弹体的应力应变随入水初始攻角的增加显著增大,入水初始攻角为6°和8°时,射弹侧面发生了显著的塑性应变,为保证研究对象在初速1400 m/s 时安全入水,初始攻角应不超过2°.