计及短周期误差的直齿轮副近周期运动及其辨识1)

刘鹏飞 朱凌云 苟向锋 石建飞 金国光

(天津工业大学机械工程学院,天津 300387)

引言

齿轮传动是机械领域应用最广泛的传动装置之一.实际加工中,不可避免地产生齿距偏差,导致齿轮传动系统工作中出现线外啮合[1];设计时预留齿侧间隙[2],易引发轮齿脱啮与齿背接触.轮齿磨损或破损会出现裂纹[3].因此,齿距偏差、齿侧间隙与轮齿裂纹等因素影响齿轮传动系统的动力学特性,进而影响齿轮传动的平稳性.

齿距偏差作为齿轮系统中最基本的误差,受到众多学者的关注[4-10],其导致齿轮出现线外啮合状态.Yu和Mechefske[5]建立了齿轮线外啮合模型,分析了线外啮合对齿轮传动的影响.周长江等[6]和Zhou 等[7]建立了线外啮合冲击模型,为计及齿距偏差的齿轮系统动力学建模及计算提供了理论基础.石照耀等[8]考虑误差激励建立了基于齿轮副整体误差的齿轮系统动力学模型.王奇斌等[9]建立了考虑齿距偏差的啮合刚度模型及齿轮转子系统动力学模型,分析了齿距偏差对齿轮传动动态特性的影响.短周期误差是以轮齿的一个齿距角为度量范围,在齿轮回转一周中出现z(z为齿数)次的一类误差,引发系统的复杂周期运动,进而影响齿轮传动平稳性[10],其引起齿轮系统的复杂周期运动的原因及分析方法亟待研究.

齿轮系统动力学模型是分析短周期误差对其动力学特性影响的基本保证.齿轮传动系统为强时变非线性系统,目前的齿轮系统模型中已考虑众多时变参量.Yi 等[11]建立了考虑时变压力角的齿轮系统动力学模型.Chen 等[12]提出了考虑由相邻轮齿齿廓偏差与轮齿修形所产生耦合效应的齿轮传动改进动力学模型.Moradi和Salarieh[13]建立考虑时变侧隙的齿轮副动力学模型.Shi 等[14]建立了含齿侧间隙与时变参量的多状态啮合直齿轮副动力学模型,分析了齿轮副的单双齿交替啮合、齿面啮合、脱啮及齿背接触状态时的动力学特性.基于以上理论基础,Liu 等[10]建立了含齿距偏差的直齿轮副时变重合度模型,并提出计及齿距偏差与时变参量的多状态啮合直齿轮副非线性动力学模型,为研究齿距偏差对齿轮副的复杂周期运动的影响提供模型基础.

非线性系统的动力学特性研究有助于判断其工作状态与稳定性[15-16].齿轮系统的平稳性决定了机械系统工作的安全性,考虑众多实际因素的齿轮系统动力学特性受到广泛研究[17-19].马锐和陈予恕[20]进行了含裂纹故障齿轮系统非线性动力学的理论与实验研究.郜志英等[21]研究了强非线性齿轮系统的倍周期分岔.Farshidianfar和Saghafi[22]分析了齿轮非线性系统的全局分岔与混沌.齿距偏差、轮齿剥落与磨损等现象影响齿轮系统的动力学特性,引起系统出现复杂的周期运动[10,23-24].Xiang 等[23]研究了考虑轮齿剥落的齿轮系统动力学特性,得出了轮齿剥落使系统的周期运动转变为复杂的概周期运动,如图1 所示.考虑磨损和裂纹的齿轮副均出现复杂周期运动,类似的复杂周期运动也出现在了考虑齿距偏差的齿轮传动系统中[10],将其定义为“近周期运动”,研究其特点及形成机理.本文的研究方法及结果可用于分析由轮齿剥落、磨损与裂纹等短周期误差引起的复杂周期运动.

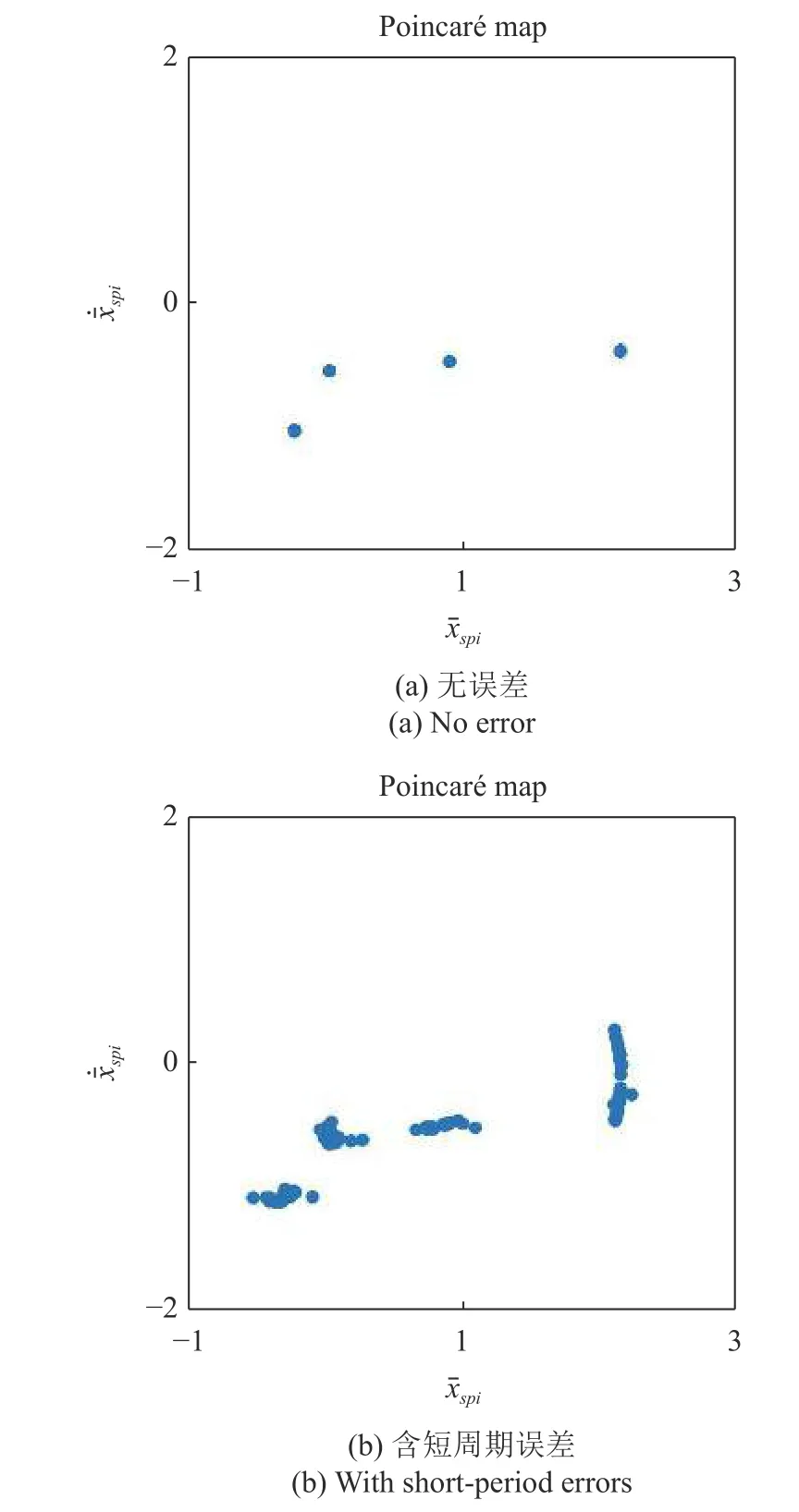
图1 含短周期误差的齿轮系统的复杂周期运动[23]Fig.1 Complex periodic motions of gear systems with short-period errors [23]

非线性系统的动力学特性受参数与初值的影响较大,其中存在大量的多稳态行为[25-26].分岔导致系统出现多稳态运动,Shi 等[27-28]研究了非线性齿轮系统在双参数平面上的多稳态运动,采用改进胞映射法精确计算出系统的吸引域,并采用多初值分岔图研究多稳态运动转迁过程.多稳态运动中的多解共存现象可通过吸引子信息与吸引域揭示[29-32].目前,对于多稳态运动的分析逐渐与工程实际结合,工程实际中的齿轮系统普遍存在齿距偏差等短周期误差,其对齿轮系统动力学特性的影响需深入研究.

本文研究短周期误差对齿轮系统周期运动的影响;针对由短周期误差引起的复杂周期运动,提出近周期运动的定义及辨识方法并分析其辨识过程;研究含齿距偏差的直齿轮副的多稳态近周期运动.引入计及齿距偏差且含时变重合度的直齿轮副非线性动力学模型[10],根据变步长4 阶Runge-Kutta 法由C 语言程序数值计算.含齿距偏差的直齿轮副近周期运动及多稳态运动通过分岔图、最大李雅普诺夫指数谱(TLE)、相图、Poincaré映射图、吸引域及分岔树状图进行研究.本文所提出的近周期运动辨识方法与分析结果为含短周期误差的齿轮系统非线性动力学研究提供理论依据.

1 近周期运动的定义及其辨识方法

1.1 近周期运动的定义

齿轮传动系统的非线性动力学中,存在一种特殊的复杂周期运动,其在长时间尺度内的周期数为n,短时间尺度内的周期为nr,将该类运动定义为近周期运动,其中n与r为正整数.

文献[10]在研究考虑齿距偏差的直齿轮副动力学特性时发现,不考虑齿距偏差时,系统周期2 运动(图2(a)中当k＞ 0.42 时)的Poincaré映射为两个离散的点;考虑齿距偏差时(如图2(b)所示),系统对应周期2 运动的Poincaré映射变为了两簇点.该类复杂的周期运动即为近周期运动.

图2 随刚度波动幅值变化的直齿轮副动力学特性[10]Fig.2 Dynamics characteristics of spur gear pair via stiffness fluctuation amplitude [10]

1.2 近周期运动的特征

齿轮传动系统的运动具有极强的周期性.不考虑轮齿误差时,每对轮齿的动力学特性和啮合特性是相同的,即其以一对轮齿啮入至啮出为一个周期,称为轮齿啮合周期.若主动轮或从动轮中仅有一个存在误差,则其以存在误差的主动轮或从动轮回转一周为周期.若主从动轮均含有误差,则以转过主从动轮齿数组合数个齿为周期,即一个完整轮齿组合周期.齿轮误差分为长周期误差与短周期误差.短周期误差为每个轮齿啮合周期出现一次的误差,长周期误差对于单个齿轮而言,为齿轮回转一周出现的误差;对于齿对而言,为每转过一个完整轮齿组合周期出现一次的误差.齿距偏差作为短周期误差对齿轮动力学特性具有很大影响.

啮合轮齿的齿距偏差值每隔一个啮合周期变化一次,即为齿轮副动力学特性分析中考察的最小时间尺度,称为微观时间尺度,即短时间尺度.不同轮齿啮合产生的相对齿距偏差值每隔一个完整轮齿组合周期变化一次,即为齿轮副动力学特性分析中考察的最大时间尺度,称为宏观时间尺度,即长时间尺度.主动轮或从动轮回转一周为介观时间尺度.通过该方式划分时间尺度,可有效分析含短周期误差齿轮副的近周期运动.

齿轮系统中的短周期误差如齿距偏差、轮齿剥落、轮齿裂纹及磨损等均会引起齿轮系统出现近周期运动,其特征主要表现为以下两点.

(1)若不考虑直齿轮副齿距偏差时,系统的周期运动数为n,则考虑直齿轮副齿距偏差时的近周期运动数亦为n,此亦即长时间尺度内的周期运动数,而其在短时间尺度内的实际运动周期数为nr.其中,r=kl-q,k为主动轮齿距偏差值分组中每组内的轮齿数,l为从动轮齿距偏差值分组中每组内的轮齿数,q为k个主动轮齿距偏差值与l个从动轮齿距偏差值组合后的相同组合值的个数.zp与zg分别为主动轮与从动轮的齿数,主从动轮的齿距偏差值按正弦规律分组分布于各轮齿,且k≤zp,l≤zg.每个长时间尺度范围内的短时间尺度取值周期为zpzg/r.

(2)不考虑齿距偏差的系统在短时间尺度内为稳定周期运动,其Poincaré映射为两个点,如图2(a)所示;含齿距偏差的系统在短时间尺度内表现为近周期运动,其Poincaré映射由两个点变为两个点簇,每个点簇中的点数量为r,如图2(b)所示.当考虑短周期误差时,在长时间尺度内考察的稳定周期运动在短时间尺度内会出现变化,长时间尺度内的周期n运动在短时间尺度表现为复杂的周期n运动,其Poincaré映射图由n个点变为n簇点,其相图由n条相轨迹变为n簇相轨迹.

1.3 近周期运动的辨识基本原理

为了辨识系统的近周期运动,定义四类不同时间尺度的Poincaré映射截面,分析宏观尺度下与微观尺度下的系统非线性动力学特性.4 类不同时间尺度的Poincaré映射截面分布为

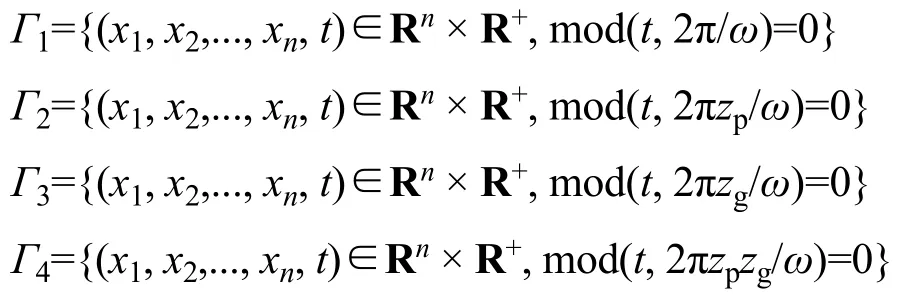
其中,ω为啮合频率,t为时间.时间映射截面Γ1为每经一个啮合周期取一次映射点,称为微观时间尺度截面;时间映射截面Γ2为主动轮每回转一周取一次映射点;时间映射截面Γ3为从动轮每回转一周取一次映射点,Γ2与Γ3为介观时间尺度截面;时间映射截面Γ4为每经过一完整轮齿组合周期取一次映射点,称为宏观时间尺度截面.

结合相图、分岔图、TLE 谱、吸引域与分岔树状图等方法辨识近周期运动.由相图与不同时间尺度Poincaré映射图可辨识系统在微观时间尺度下的运动周期数及宏观时间尺度下的实际运动周期数,并判断系统的相轨迹拓扑结构、速度位移变化及轮齿多状态啮合情况;通过分岔图与TLE 谱判断系统处于周期运动或混沌运动,进一步辨识系统在不同时间尺度下随参数变化的近周期运动,并分析系统在长时间尺度与短时间尺度内的动力学特性;由吸引域与分岔树状图得出系统随参数变化的多稳态近周期运动转迁过程,结合分岔图与TLE 谱辨识吸引域的实际周期数及实际吸引子数量.该辨识方法也可用于分析其他短周期误差引起的近周期运动.

2 计及齿距偏差的直齿轮副动力学模型

直齿轮副的简化物理模型如图3 所示.其中,Tp与Tg分别为输入、输出转矩,Ip与Ig分别为主从动齿轮的转动惯量,Op与Og分别为主从动齿轮的中心,θp与θg分别为主从动齿轮的角位移,Rbp与Rbg分别为主从动齿轮的基圆半径,k(τ)为时变啮合刚度,cg为啮合阻尼;e(τ)为时变综合传递误差,为齿侧间隙半值,μ为摩擦系数.

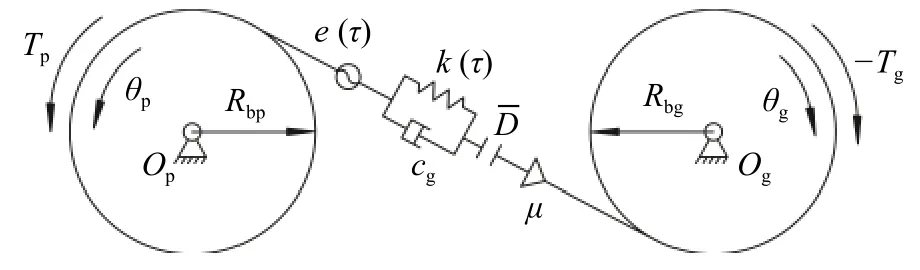
图3 齿轮副简化物理模型Fig.3 Simplified physical model of gear pair

设主从动齿轮的极限齿距偏差值分别为ΔFpt1与ΔFpt2,则主从动齿轮的齿距偏差函数分别为

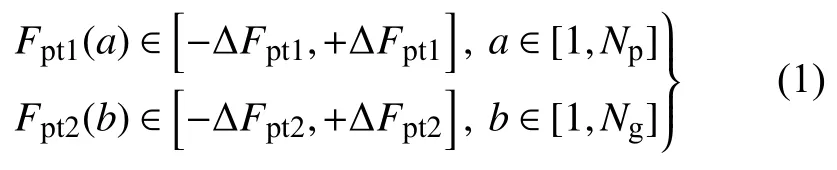
其中,Ni∈(1,zi) (i=p,g)为主从动齿轮齿距偏差互不相同值的个数,则任意两轮齿啮合时的相对齿距偏差值为

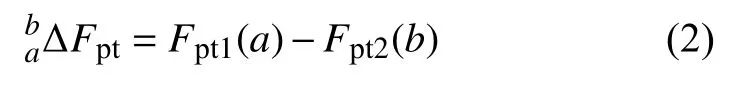
其中,为相互啮合的两个轮齿的齿距偏差值叠加所形成的组合值,其可能的取值数量

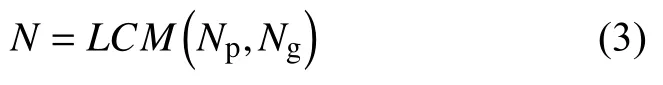
式中LCM()为最小公倍数的计算函数.齿轮从初始状态啮合,啮合次数为N时,完成一个完整轮齿组合周期,其最大取值为zpzg-1 .

计及齿距偏差的直齿轮副非线性动力学模型为

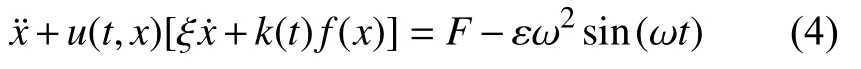
其中,u(t,x)为含齿距偏差直齿轮副啮合状态函数,f(x)为齿侧间隙函数,分别为

3 计及齿距偏差的直齿轮副近周期运动

3.1 直齿轮副的近周期运动辨识

本节对计及齿距偏差的直齿轮副近周期运动进行辨识.以本实验室试验台中的齿轮副为研究对象,其参数如表1 所示.主从动轮的极限齿距偏差值分别为ΔFpt1=± 9 μm 与ΔFpt2=± 10 μm,Np=21,Ng=26,a∈[1,21],b∈ [1,26] .主从动轮的齿距偏差值如表2与表3 所示.考虑齿距偏差的直齿轮副在Γ1，Γ2，Γ3与Γ4截面下随刚度波动幅值变化的分岔图与TLE 谱分别如图2(b)、图4(a)与图4(b)所示.Γ1截面下的映射点由蓝色表示;Γ2截面下的映射点由紫色表示;Γ3截面下的映射点由天蓝色表示;Γ4截面下的映射点由红色表示.

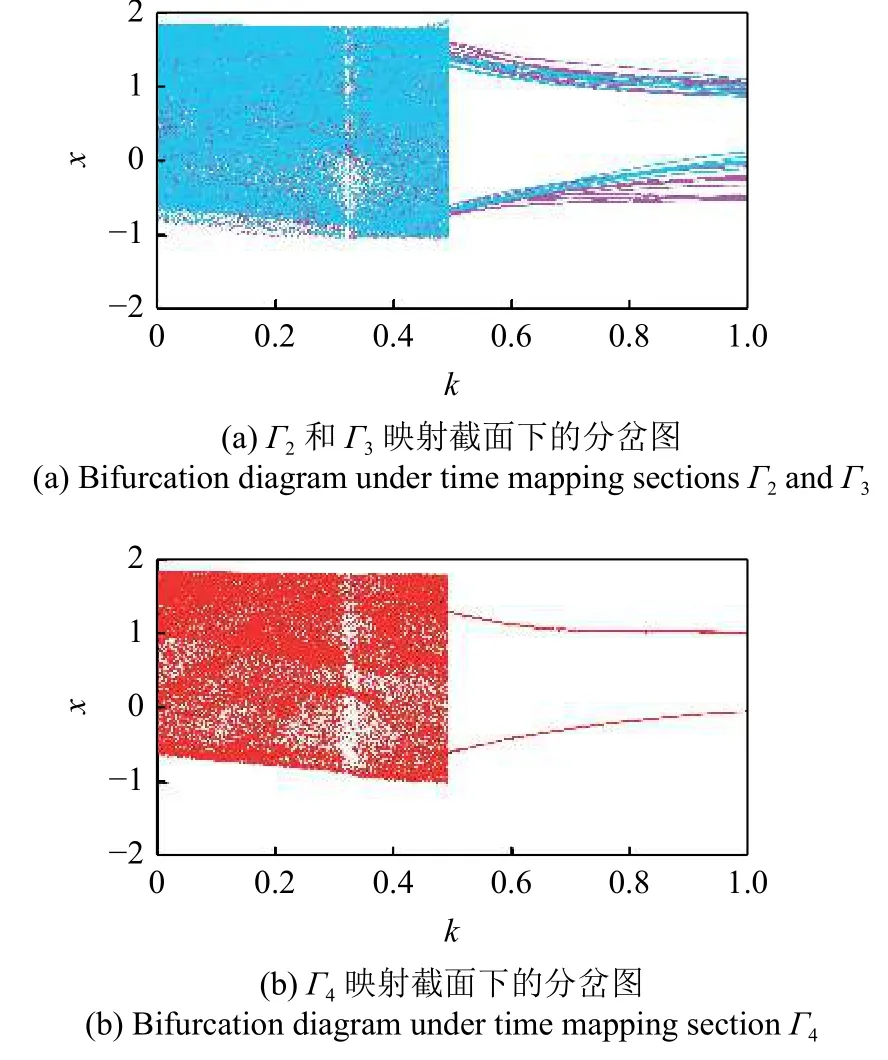
图4 随刚度波动幅值变化的直齿轮副多时间尺度分岔图Fig.4 Bifurcation diagrams of the spur gear pair with different time scales via stiffness fluctuation amplitude

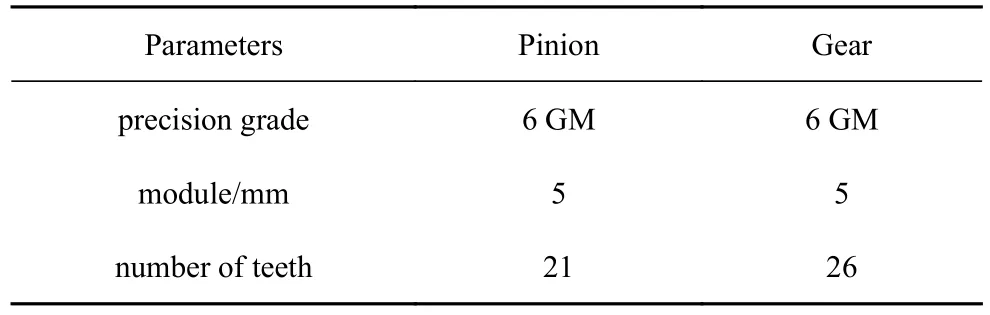
表1 齿轮参数Table 1 Parameters of a spur gear pair

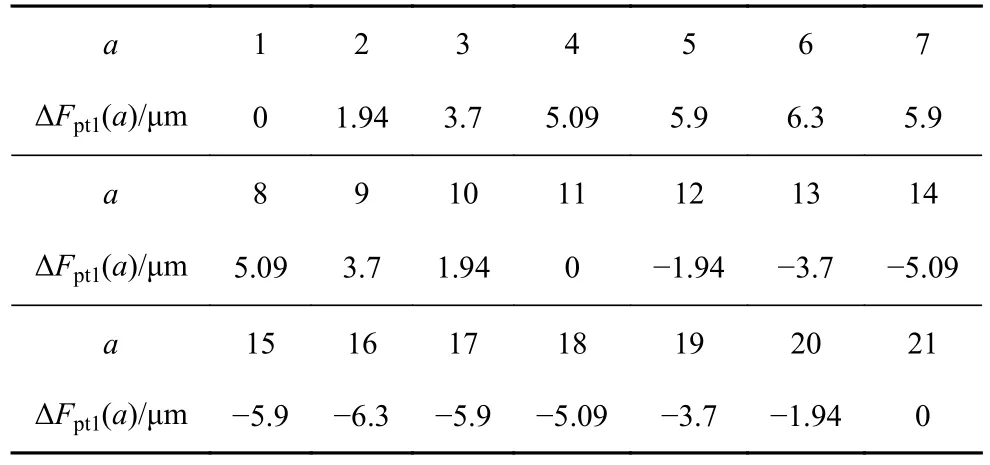
表2 主动轮齿距偏差值(Np=21)Table 2 Pitch deviation values of the pinion (Np=21)

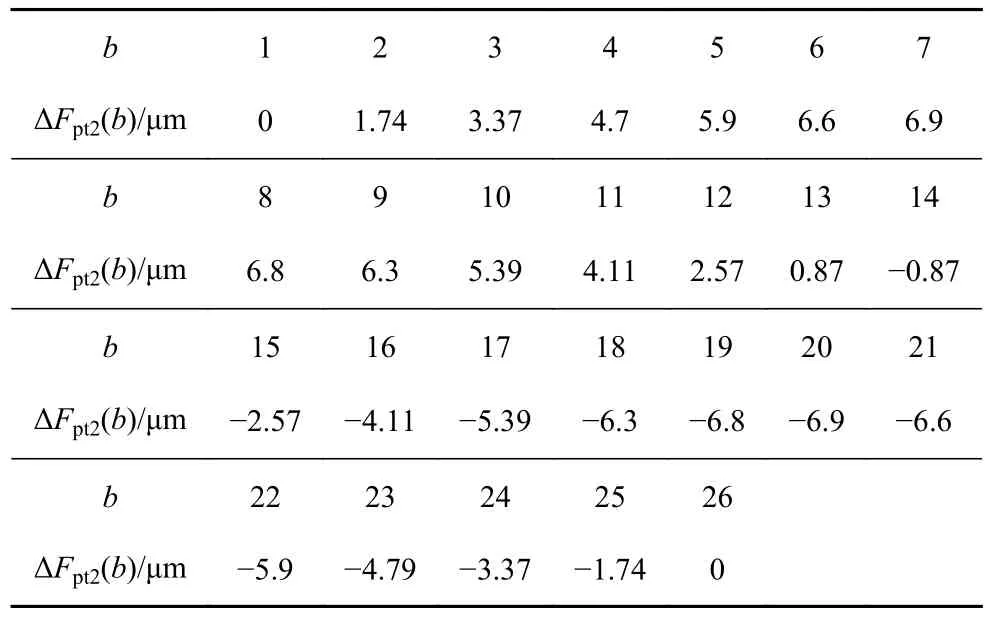
表3 从动轮齿距偏差值(Ng=26)Table 3 Pitch deviation values of the gear (Ng=26)

随着刚度波动幅值的增大,系统的混沌运动均经鞍结分岔退化为周期运动.系统在微观时间尺度(Γ1截面)的分岔图中,周期运动的映射点数量较多,在两个区域内出现点簇,表现为近周期2 运动,如图2(b)所示.由于短周期误差的存在,系统的周期运动较复杂,齿轮传动平稳性较差.当时间尺度增大时,分岔图取Γ2截面,近周期2 运动在Γ2截面下的每个点簇中的映射点数量相对Γ1截面减少,因为此时已忽略了主动轮的影响,如图4(a)所示.取Γ3截面时,每个点簇中的映射点数量相对Γ2截面继续减少,这是因为此时忽略了从动轮的影响,而从动轮上齿距偏差分布比主动轮上复杂.当时间尺度取一个完整轮齿组合周期时,分岔图中的周期运动映射点数为2,表现为周期2 运动,如图4(b)所示,因为此时已忽略了主从动轮每个轮齿的差异.可见,系统在微观时间尺度内的近周期2 运动在宏观时间尺度内为周期2 运动.系统的实际运动周期为宏观时间尺度内的Poincaré映射点数;微观时间尺度内的映射点为对应宏观时间尺度内映射点数的点簇.

通过近周期运动辨识方法进一步分析含齿距偏差的直齿轮副随扭矩变化的动力学特性,如图5 所示.由图可见,当扭矩较小时,系统呈现混沌运动.在微观时间尺度内,系统经鞍结分岔由混沌运动退化为近周期2 运动,再经逆倍化分岔退化为近周期1 运动,如图5(a)所示.Γ2与Γ3截面内系统的动力学特性如图5(b)所示,系统由混沌运动退化为近周期2 运动,再退化为近周期1 运动,由图5(b) 中A与B局部放大所示,Γ3截面的每个点簇的映射点数量小于Γ2截面的每个点簇的映射点数量.对照图5(a)和图5(b)可见,周期运动分岔图的线宽明显减小.当时间尺度继续增大时,选取Γ4截面,系统经鞍结分岔由混沌运动退化为周期2 运动,再经逆倍化分岔退化为周期1 运动,如图5(c)所示.由宏观时间尺度Poincaré映射截面辨识系统的近周期2 运动为周期2 运动.考虑齿距偏差的直齿轮副实际动力学特性表现为:混沌运动→周期2 运动→周期1 运动.

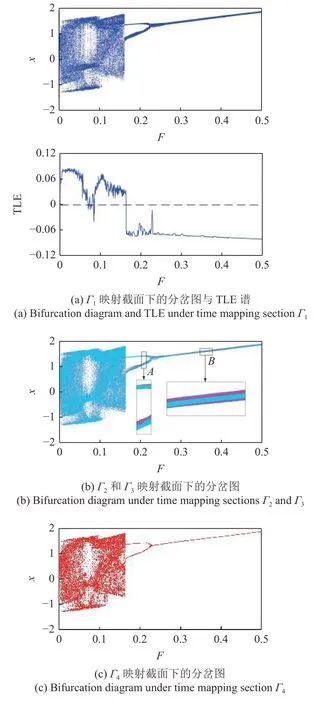
图5 随扭矩变化的直齿轮副多时间尺度分岔图Fig.5 Bifurcation diagrams of the spur gear pair with different time scales via torque

系统在不同时间尺度Poincaré映射截面下随啮合频率变化的分岔图及对应的TLE 谱如图6 所示.当啮合频率较小时,系统在微观时间尺度内表现为明显的近周期1 运动,如图6(a)所示.随着时间尺度的增大,近周期1 运动的点簇中映射点数量逐渐减少,如图6(b)所示.随着啮合频率的增大,微观时间尺度下的系统近周期1 运动经倍化分岔进入近周期2 运动,再经鞍结分岔通向混沌运动,随后经逆倍化序列退化为近周期3 运动,最后经周期跳跃退化为近周期1 运动.

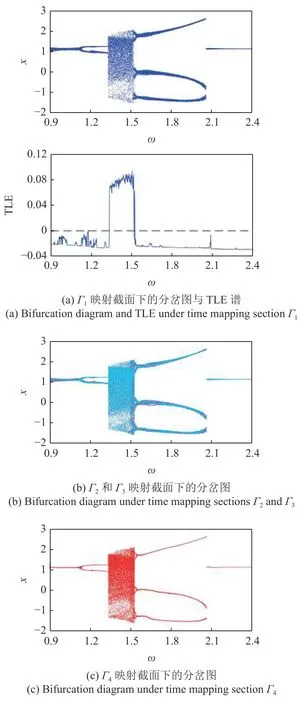
图6 随啮合频率变化的直齿轮副多时间尺度分岔图Fig.6 Bifurcation diagrams of the spur gear pair with different time scales via meshing frequency

在宏观时间尺度下,系统的近周期运动被辨识为周期运动,如图6(c)所示.系统在宏观时间尺度内的动力学特性表现为周期1 运动→周期2 运动→混沌运动→周期6 运动→周期3 运动→周期1 运动.

由图4～ 图6可得,短周期误差对周期运动的影响较大,使其变复杂.由于混沌运动本身为复杂的非周期运动,短周期误差对于混沌运动的影响不明显.由此可见,相对于宏观时间尺度内的系统动力学特性,短周期误差在微观时间尺度内影响齿轮传动的平稳性.

综上所述,含短周期误差的直齿轮副出现较为复杂的近周期运动.近周期运动辨识方法可有效地分析并判断系统在微观时间尺度与宏观时间尺度内的动力学特性.系统的实际运动周期数为宏观时间尺度内的Poincaré映射点数或微观时间尺度内的Poincaré映射点簇数.下一节将进一步研究含短周期误差的直齿轮副多稳态近周期运动.

3.2 直齿轮副的多稳态近周期运动

非线性系统在不同状态变量初值下会出现多种稳定状态.短周期误差使系统出现多稳态近周期运动,影响系统的稳定性.本节主要研究含齿距偏差的直齿轮副多稳态近周期运动,通过多初值分岔图、多初值TLE 谱、吸引域、相图、Poincaré映射图及分岔树状图分析系统的动力学特性.为了使结果具有普遍性,齿距偏差取值为Np=21,Ng=13,a∈[1,2],b∈[1,3].主从动轮的具体齿距偏差值分别如表2与表4 所示.状态平面内的吸引域及吸引子信息可通过改进胞映射法计算得出,状态域 Ω 被平均分为600 × 600 个胞,所考察的状态域范围建立为Ω ∈{-3 ≤x≤3,-3 ≤≤3},该状态域包含系统所有可能出现的状态值.

表4 从动轮齿距偏差值(Ng=13)Table 4 Pitch deviation values of the gear (Ng=13)

考虑齿距偏差的直齿轮副随扭矩变化的动力学特性如图7～图9 所示.参数取ω=1.2,k=0.3,ξ=0.2,ε=0.2,μ=0.12 与D=1.系统多初值分岔如图7所示.

图7 中Sn 与Pn 表示混沌运动;PNn,QNn和RNn表示近周期n运动.Bij表示普通分岔点,Gij,Hij,Kij和Mij表示共存吸引子发生变化的分岔点,i和j代表系统在分岔点前后的运动状态.多初值分岔图对应吸引域如图8 所示,可表示系统出现多稳态运动时的吸引子与吸引域演变规律.为了更直观地说明系统运动转迁过程,构建分岔树状图,如图9所示.

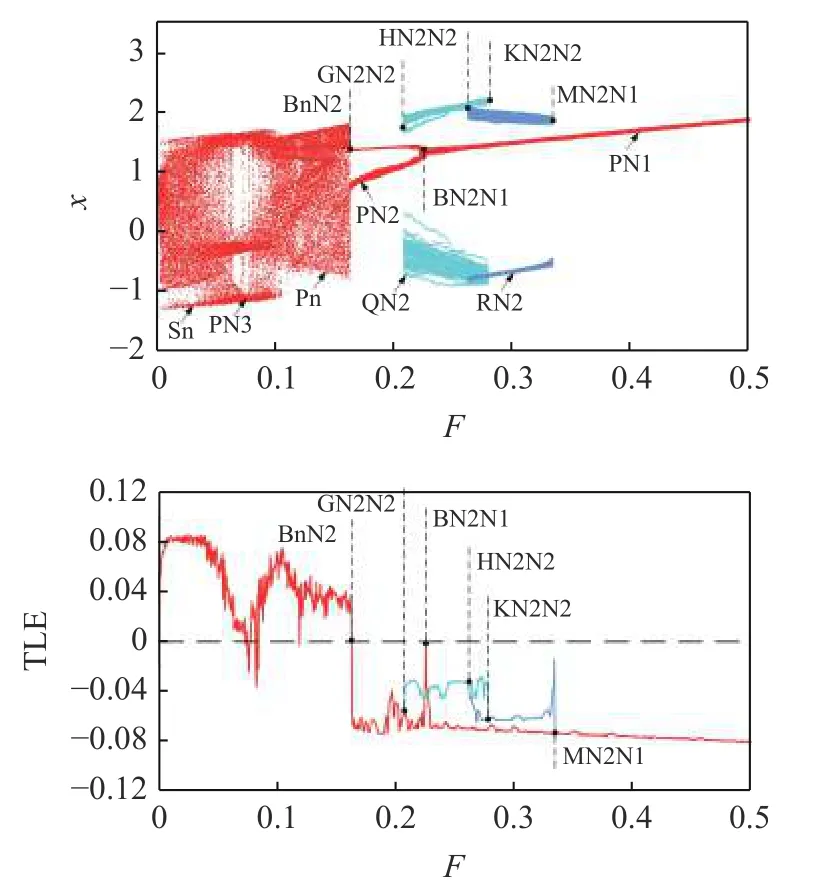
图7 系统随扭矩变化的多初值分岔图及TLE 谱Fig.7 Multi-initial values bifurcation diagrams and TLE spectrums of system via F

当扭矩较小时,系统出现混沌运动(Sn),经过周期窗口(PN3)后,逐渐演变为另一混沌运动(Pn).系统的Pn 运动在BnN2 点经鞍结分岔退化为近周期2 运动(PN2),分岔图中的Poincaré映射点表现为两个点簇.在GN2 N2 点,系统出现两种近周期2 运动共存(PN2 与QN2),对应吸引域及吸引子信息如图8(a)所示,红色代表PN2 运动,“▲”表示PN2 运动吸引子;青色代表QN2 运动,“○”表示QN2 运动吸引子.QN2 运动吸引子及Poincaré映射点更为复杂,系统处于QN2 运动时受齿距偏差影响较大,近周期更为明显,导致齿轮传动不平稳.在BN2 N1 点,系统的PN2 运动经逆倍化分岔退化为近周期1 运动(PN1),“◇”表示PN1 运动吸引子,系统出现PN1 运动与QN2 运动共存,如图8(b) 所示.在HN2 N2 点,系统出现三稳态运动,即近周期1 运动(PN1)与两种近周期2 运动(RN2 与QN2)共存,宝蓝色代表RN2 运动,“△”表示RN2 运动吸引子,如图8(c)所示.QN2 运动吸引域被RN2 运动吸引域侵蚀,系统出现QN2 运动的可能性减小.RN2 运动与QN2 运动的吸引子均呈现两个区域的点簇.在KN2 N2 点,QN2 运动消失,系统出现RN2 运动与PN1 运动共存,如图8(d) 所示.在MN2 N1 点,RN2 运动退化为PN1 运动,系统仅存在一种相对平稳的PN1 稳态运动.随着扭矩的增大,系统的近周期运动逐渐不明显.在扭矩较大时,齿距偏差对系统运动平稳性的影响较小.

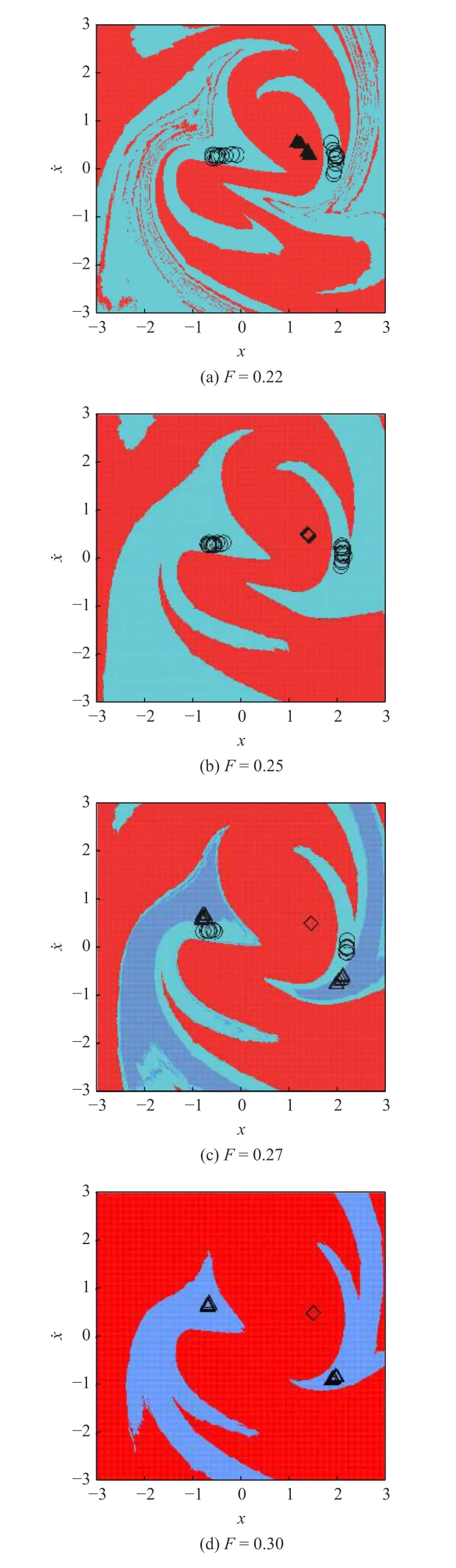
图8 系统随扭矩变化的吸引域Fig.8 Basin of attraction of system via F

通过构建分岔树状图可更直观地表示系统的运动转迁过程.红色框表示共存吸引子出现或消失的分岔点;黑色框表示普通分岔点;蓝色圈为混沌与近周期解;黄色框为相同转迁过程.含齿距偏差的直齿轮副随扭矩变化的运动转迁过程如图9 所示.

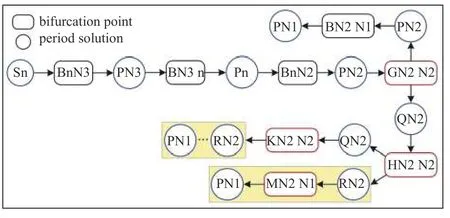
图9 系统随扭矩变化的分岔树状图Fig.9 Bifurcation dendrogram of system via F

多初值分岔图中的红色部分的稳态运动转迁路径为:Sn→BnN3→PN3→BN3 n→Pn→BnN2→PN2→GN2 N2→PN2→BN2 N1→PN1.多初值分岔图中的青色部分的稳态运动转迁路径为:Sn→BnN3→PN3→BN3 n→Pn→BnN2→PN2→GN2 N2→QN2→HN2 N2→QN2→KN2 N2→RN2→MN2 N1→PN1.多初值分岔图中的宝蓝色部分的稳态运动转迁路径为:Sn→BnN3→PN3→BN3 n→Pn→BnN2→PN2→GN2 N2→QN2→HN2 N2→RN2→MN2 N1→PN1.

受齿距偏差的影响,系统出现复杂的多稳态近周期运动,共3 种共存吸引子.当扭矩较小时,系统表现为混沌运动,多稳态近周期运动较为复杂,导致齿轮传动平稳性降低.当扭矩较大时,系统表现为单稳态运动,且近周期运动不明显,齿轮传动平稳性相对较好.含齿距偏差系统的多初值分岔图中的Poincaré映射点表现为点簇,对应的吸引子亦表现为点簇形式,系统运动状态受初值的影响较大.

含齿距偏差的直齿轮副随啮合频率变化的动力学特性如图10～图13 所示.参数选取为:F=0.15,k=0.1,ξ=0.07,ε=0.15,μ=0.15 与D=1.系统的多初值分岔及对应的TLE 谱如图10 所示.多初值分岔图对应的吸引域、相轨迹及Poincaré映射如图11 与12 所示.分岔树状图如图13 所示.根据式(6)与图12中的相轨迹,当轮齿相对位移x始终大于齿侧间隙半值D时,齿轮副始终处于齿面啮合状态;当轮齿相对位移x小于齿侧间隙半值D且大于齿侧间隙负半值-D时,齿轮副出现轮齿脱啮状态;当轮齿相对位移x小于齿侧间隙负半值-D时,齿轮副出现齿背接触状态.

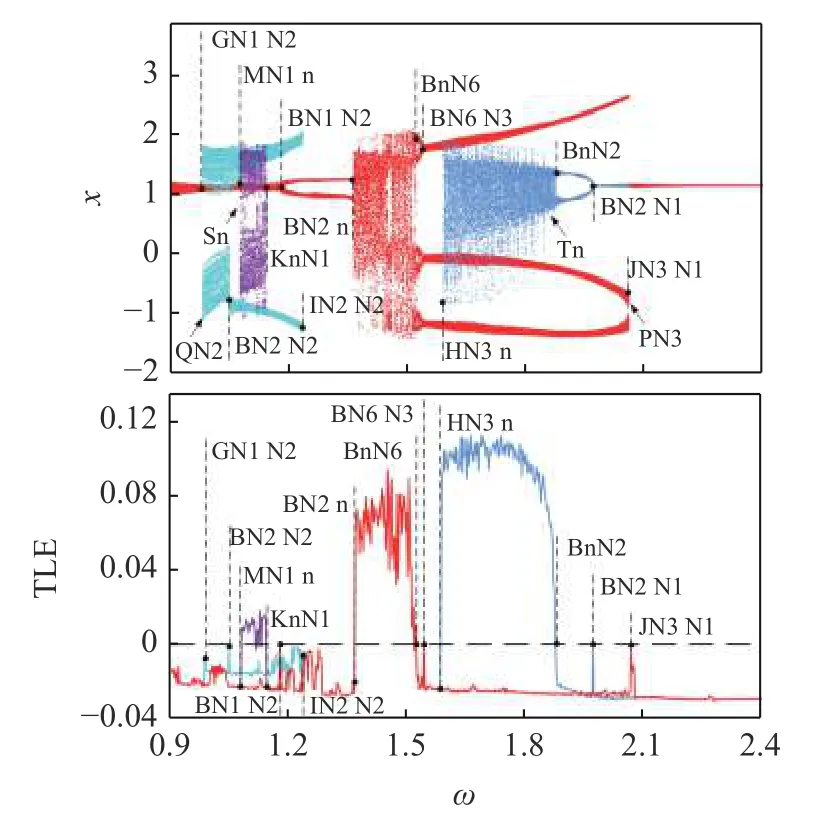
图10 系统随啮合频率变化的多初值分岔图及TLE 谱Fig.10 Multi-initial values bifurcation diagrams and TLE spectrums of system via ω

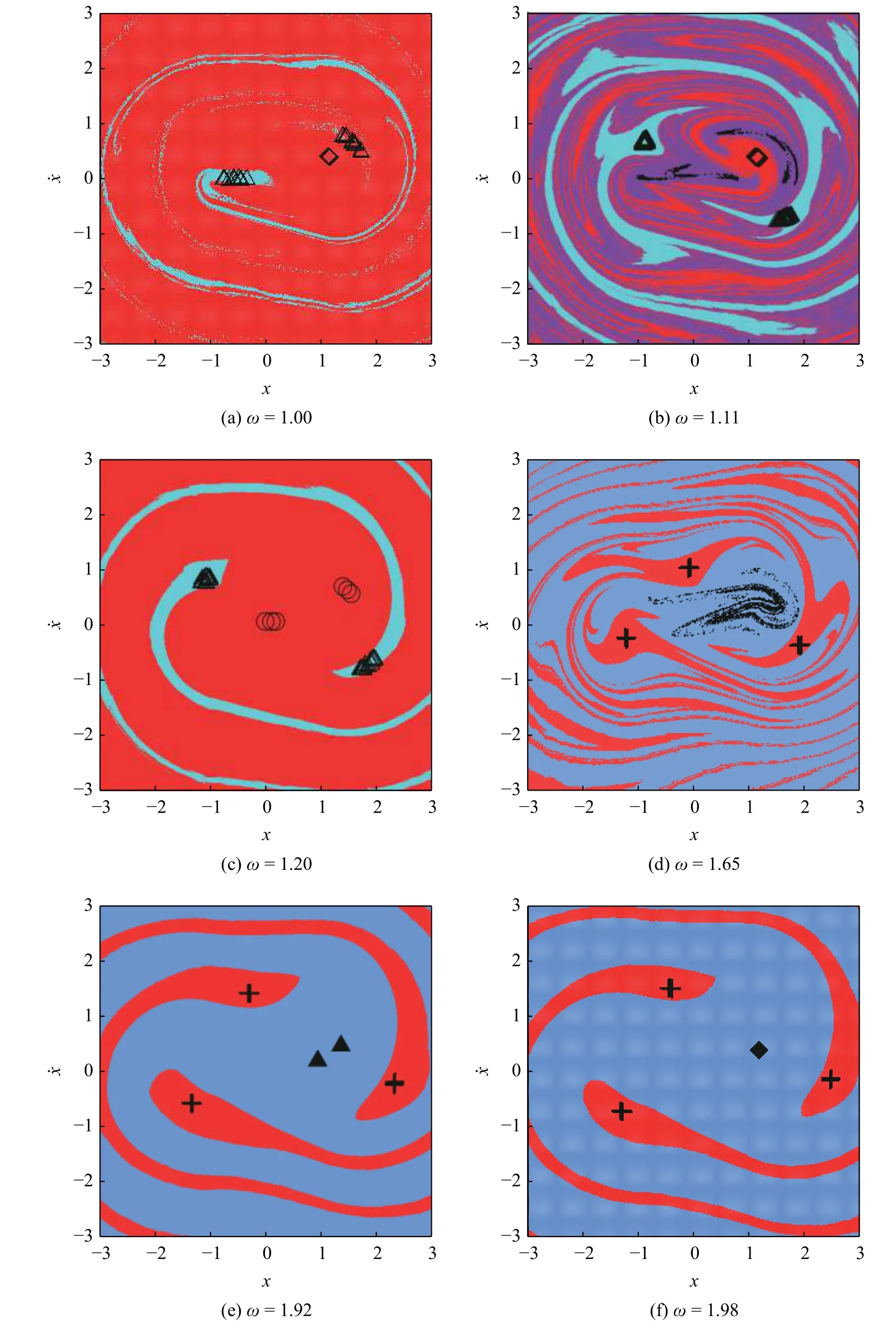
图11 系统随啮合频率变化的吸引域Fig.11 Basin of attraction of system via ω

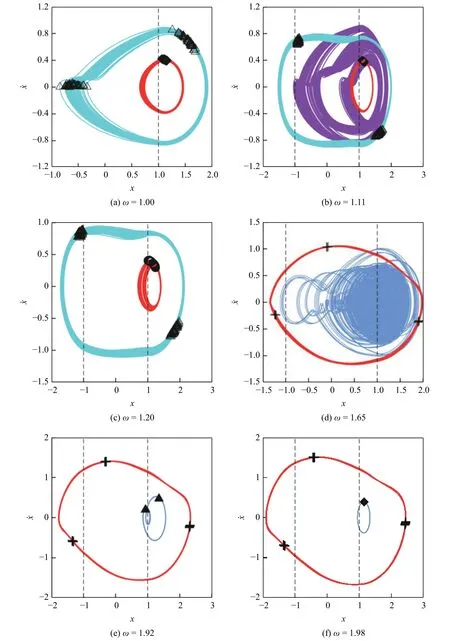
图12 系统随啮合频率变化的相图与Poincaré映射图Fig.12 Phase portraits and Poincaré maps of system via ω

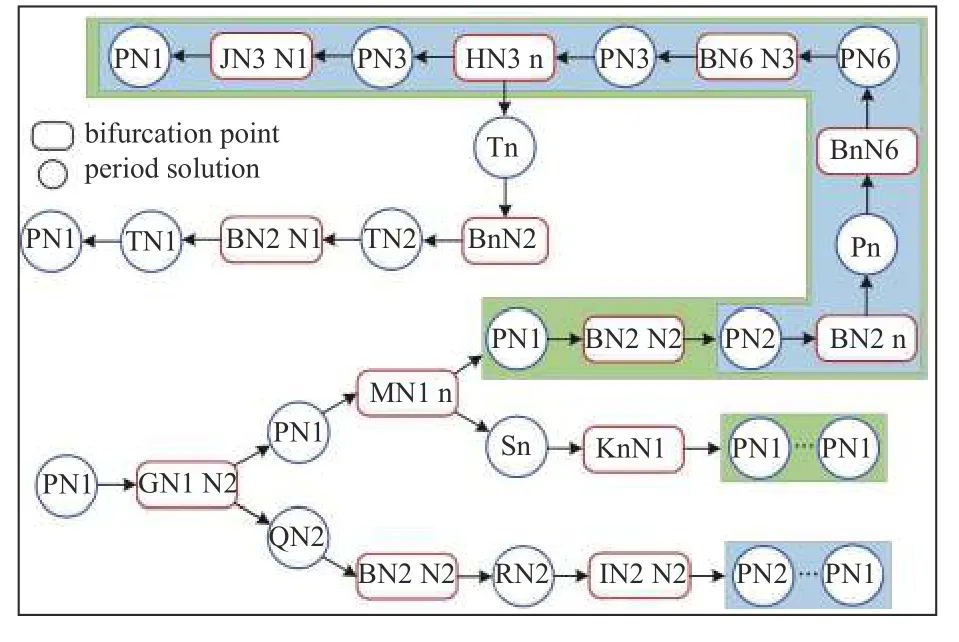
图13 系统随啮合频率变化的分岔树状图Fig.13 Bifurcation dendrogram of system via ω

图中Sn,Pn 与Tn 表示混沌运动;PNn,QNn,RNn和TNn表示近周期n运动.Gij,Mij,Hij,Kij,Jij和Iij表示共存吸引子发生变化的分岔点.当啮合频率较小时,系统仅存在一种稳态运动,表现为近周期1 运动(PN1).在GN1 N2 点,系统出现两种稳态运动,即近周期1 运动与近周期2 运动共存(PN1 与QN2),且QN2 运动的近周期现象更明显,对应的吸引域及吸引子信息如图11(a)所示,红色代表PN1 运动,“◇”表示PN1 运动吸引子;青色代表QN2 运动,“△”表示QN2 运动吸引子.PN1 运动的吸引域面积较大,其存在的可能性较大,QN2 运动的每个点簇中的吸引子数量较多.齿轮副处于QN2 运动时的脱啮程度大于PN1 运动,且QN2 运动相轨迹

更为复杂,因此,齿轮副处于QN2 运动时的传动平稳性较差,如图12(a)所示.由于QN2 吸引域的面积相对较小,齿轮副出现传动不平稳的可能性较低.

在BN2 N2 点,QN2 运动演变为RN2 运动,在MN1 n 点,系统出现近周期1 运动(PN1),近周期2 运动(RN2)与混沌运动(Sn)共存,此时,青色代表RN2 运动;紫色代表Sn 运动,“·”表示Sn 运动吸引子.RN2 运动的吸引域面积增大,PN1 运动的吸引域被Sn 运动的吸引域侵蚀,如图11(b)所示.系统处于RN2 运动与Sn 运动均出现齿背接触,且RN2 运动的齿背接触程度较大,而系统处于PN1 运动时仅存在脱啮状态且脱啮程度较小,如图12(b)所示.当系统处于RN2 运动与Sn 运动时,齿轮传动不平稳.在KnN1 点,Sn 运动退化为PN1 运动,系统出现RN2 运动与PN1 运动共存.在BN1 N2 点,近周期1 运动(PN1)经倍化分岔进入近周期2 运动(PN2),系统出现两种近周期2 运动(PN2 与RN2)共存,对应吸引域如图11(c)所示,“○”表示PN2 运动吸引子.系统处于RN2 运动时出现脱啮及齿背接触状态,而系统处于PN2 运动时仅出现脱啮状态,如图12(c)所示.由于PN2 运动的吸引域面积相对较大,系统处于PN2 运动的可能性较大,齿轮传动平稳的可能性亦较大.在IN1 N2 点,RN2 运动演变为PN2 运动,系统仅存在近周期2 运动(PN2).

系统在BN2 n 点经鞍结分岔进入混沌运动,在BnN6 点经逆倍化序列退化为近周期运动,并在BN6 N3 点退化为近周期3 运动(PN3).在HN3 n 点,系统出现近周期3 运动与混沌运动(Tn)共存,对应吸引域如图11(d)所示,此时,红色代表PN3 运动,“+”表示PN3 运动吸引子;宝蓝色代表Tn 运动,“·”表示Tn 运动吸引子.系统处于PN3 运动与Tn 运动时均出现齿背接触状态,如图12(d)所示,系统处于Tn 运动状态时的齿轮传动平稳性较差.在此啮合频率下,Tn 运动的吸引域面积较大,齿轮出现传动不平稳的可能性大.系统的混沌运动在BnN2 点经逆倍化序列退化为近周期2 运动(TN2),系统出现近周期3 运动(PN3)与近周期2 运动(TN2)共存,此时,宝蓝色代表TN2 运动,“▲”表示TN2 运动吸引子,如图11(e)所示.系统处于PN3 运动时仍存在齿背接触状态,而系统处于TN2 运动时仅存在脱啮状态,如图12(e)所示.由于PN3 运动的吸引域面积较小,齿轮出现传动不平稳的可能性较小.

在BN2 N1 点,TN2 运动经逆倍化分岔退化为近周期1 运动(TN1),宝蓝色代表TN1 运动,“◆”表示TN1 运动吸引子,如图11(f)所示,系统的近周期运动逐渐消退,齿距偏差对系统周期运动的影响继续减小.系统处于PN3 运动时仍存在齿背接触状态,而系统处于TN1 运动时仅存在脱啮状态且脱啮程度减小,如图12(f)所示.TN1 运动吸引域面积较大,齿轮传动平稳性继续增大.系统的PN3 运动在JN3 N1 点退化为PN1 运动,同时TN1 运动转为PN1 运动,系统仅存在一种稳态运动,即近周期1 运动(PN1).系统随啮合频率变化时出现复杂的多稳态运动,影响齿轮传动平稳性.随着啮合频率增大,齿距偏差对齿轮传动平稳性的影响逐渐减小.

系统随啮合频率变化的运动转迁过程可通过分岔树状图表示,如图13 所示.蓝色框与绿色框表示相同运动转迁过程.

多初值分岔图的红色部分稳态运动转迁路径为:

PN1→GN1 N2→PN1→MN1 n→PN1→BN1 N2→PN2→BN2 n→Pn→BnN6→PN6→BN6 N3→PN3→HN3 n→PN3→JN3 N1→PN1.

多初值分岔图的青色部分稳态运动转迁路径为:PN1→GN1 N2→QN2→BN2 N2→RN2→IN2 N2→PN2→BN2 n→Pn→BnN6→PN6→BN6 N3→PN3→HN3 n→PN3→JN3 N1→PN1.

多初值分岔图的紫色部分稳态运动转迁路径为:PN1→GN1 N2→PN1→MN1 n→Sn→KnN1→PN1→BN1 N2→PN2→BN2 n→Pn→BnN6→PN6→BN6 N3→PN3→HN3 n→PN3 →JN3 N1→PN1.

多初值分岔图的宝蓝色部分稳态运动转迁路径为:PN1→GN1 N2→PN1→MN1 n→ PN1→BN1 N2→ PN2→BN2 n→Pn→BnN6→PN6→BN6 N3→PN3→ HN3 n→Tn→BnN2→TN2→BN2 N1→TN1→PN1.

含齿距偏差的直齿轮副随啮合频率变化时出现4 种稳态运动.受齿距偏差影响,系统的周期运动较为复杂,对应于QN2 与RN2 的近周期运动更为明显.当啮合频率处于敏感参数范围内,系统容易出现多解共存的情况,引起多稳态运动的发生.齿距偏差增加了系统在微观时间尺度内的相轨迹数量、吸引子数量及Poincaré映射点数,使其呈现线簇或点簇形式,导致复杂的周期运动.初值对系统运动影响较大,当系统处于不同稳态运动时,会导致不同程度的脱啮与齿背接触发生.当系统处于敏感参数范围内,更易出现脱啮与齿背接触及混沌运动状态,导致齿轮传动平稳性降低.合理的啮合频率范围及初值范围可提高直齿轮副传动的平稳性.

4 结论

本文提出近周期运动的定义及其辨识方法,分析了近周期运动的辨识过程,并研究了系统在参数与初值影响下的多稳态近周期运动,结论如下所示.

(1)齿距偏差作为齿轮副的短周期误差导致系统出现近周期运动.当齿轮副中考虑齿距偏差时,在长时间尺度范围内考察的稳定周期运动在短时间尺度内会发生变化.长时间尺度内的周期n运动在短时间尺度内其Poincaré映射图由n个点变为n簇点,其相图由n条相轨迹变为n簇相轨迹.通过近周期运动辨识方法,可有效地判断系统在微观时间尺度与宏观时间尺度内的动力学特性.系统的实际运动周期数为宏观时间尺度的Poincaré映射点数或微观时间尺度的Poincaré映射点簇数.

(2)受短周期误差影响,系统出现复杂的多稳态近周期运动.当扭矩或啮合频率处于敏感取值范围内,系统易出现多解共存的情况,导致其出现多稳态运动.齿距偏差增加了系统在微观时间尺度内的相轨迹数量、吸引子数量及Poincaré映射点数,导致齿轮传动平稳性降低.通过吸引域可分析系统运动转迁过程并判断各稳态出现的可能性.当系统处于敏感参数及初值范围内,直齿轮副容易出现脱啮、齿背接触与混沌运动状态.合理的参数范围及初值范围可提高齿轮传动的平稳性.