带冷却气流的亥姆霍兹共振器的声类比模型1)
甘振鹏 杨 东
(南方科技大学工学院力学与航空航天工程系,广东深圳 518055)
引言
为响应国家碳达峰、碳中和目标下对烟气污染治理的需求,低污染排放的燃气轮机和航空发动机的发展日益需要满足更严格的环保要求[1].相比于传统燃烧方式,贫燃预混燃烧因能显著降低NOx排放而被广泛应用[2-3].但贫燃预混燃烧会使燃烧室更容易受到热声振荡的影响—不稳定燃烧产生声音,该声音传到燃烧室边界被反射回来进一步扰动燃烧进而产生更多声音;该正反馈过程可能产生巨大的压力振荡[4].燃烧热声振荡所造成的危害小到干扰燃烧过程,产生机械振荡和噪音,使污染控制失效,大到减少部件工作寿命,损坏燃烧室部件,甚至导致发动机停机以及严重空难事故[5].实现贫燃预混燃烧的关键技术之一是避免和抑制燃烧热声振荡.
抑制燃烧热声振荡的方法主要有主动控制和被动控制.亥姆霍兹共振器(HR)由于其简单的结构、较高的经济性和良好的吸声性能而被作为一种典型的抑制热声振荡的被动控制装置[6].HR 的结构一般由空腔加上颈部开孔所组成,其共振频率可以用众所周知的公式f=c/(2π)进行预测,其中c为HR 空腔中的声速,而A,l,V分别是HR 颈部截面积,HR 颈部长度和HR 空腔体积.在共振频率附近,HR 入口附近一个微小的压力扰动会引起其颈部显著的质量流量扰动[7],从而由于黏性效应而耗散掉声波能量[8].将HR 应用于上述燃烧室中消除热声振荡时,在HR 的背部空腔中往往会输入取自于压气机后几级的冷却气流,其温度(约500 K 左右)一般显著低于燃烧室温度(约1000~2100 K)[9].这些冷却气流不仅可以保护HR 免于燃烧室内高温燃气的侵蚀,还能为HR 提供平均流动以提高其吸声性能.根据HR 中有无平均流动,可分为线性模型(有平均颈流的情况,也称为偏流)和非线性模型(无偏流)[10-15].而在以往的工作中,往往忽视了热声振荡系统中HR 与燃烧室之间的温差.比如,Dupere和Donwling[13]基于燃烧室内一维扰动量在共振器上下游之间的质量守恒和滞止焓连续关系,得到的共振器模型无法考虑前述温差带来的影响.但实际上,HR和燃烧室的温差对燃烧室内声波(及熵波)传播的影响不可忽视.最近,Yang 等[16-17]考虑了HR 与燃烧室的温差对燃烧室声波的影响,并针对HR 与燃烧室之间有温差的情况,将能量守恒方程与一维燃烧室中的质量、动量守恒方程相结合,推导出一个一维声场中跨过HR 时的阶跃条件模型,该模型将燃烧室的上、下游熵波与声波传递关系转化为一系列声传递矩阵,来研究该温差对HR 性能的影响.该研究表明共振器与燃烧室之间的温差会在燃烧室内共振器下游产生显著的熵波,与此同时,共振器影响燃烧室内声波传播的性能也被显著地改变了.
但上述阶跃条件模型无法从机理上解释为何共振器下游会产生熵波,更无法解释该熵波的产生如何改变共振器对燃烧室内声波传播的影响.针对这些问题,本工作将采用声类比方法[18-19],通过质量、动量和能量守恒,推导出安装有亥姆霍兹共振器的一维燃烧室管道内的声类比形式的波动方程.该方程的源项即表示了共振器对管道内声场影响的物理机理.然后通过引入HR 的线性模型和相关热力学方程,以及系统边界条件,便可使相关方程组闭合.对该波动方程作傅里叶变换至频域中,将解偏微分问题转化为解常微分问题,可以直观解得方程的解,即燃烧室中HR 上、下游扰动量之间的关系.该方程具有声类比的形式,在其右侧可以直观地看到声源和声耗散项,进而得到HR 所带来的熵扰动和质量扰动对管道内声场的影响.最后,通过与文献[16]的阶跃条件模型结果做对比来验证该模型.
1 理论模型
1.1 安装有亥姆霍兹共振器的一维管道声波模型
考虑一个安装于主系统(此处为一个一维燃烧室管道)上的HR,低于燃烧室内部温度的冷却气流从HR 空腔后部穿过HR 进入燃烧室,如图1 所示.
图1 中,M为马赫数,p为压力,T为温度,S为熵,Ac和An分别为燃烧室截面面积和HR 颈部截面面积,L为HR 颈部的长度,顶标“-”和“~”分别表示平均量和扰动量.在燃烧室中,位于共振器上游的流量参数下标为1,共振器下游下标为2,HR 共振器颈部下标为n,分别对应如图2 所示的控制体的截面1-1,截面2-2和源项处的流量参数.
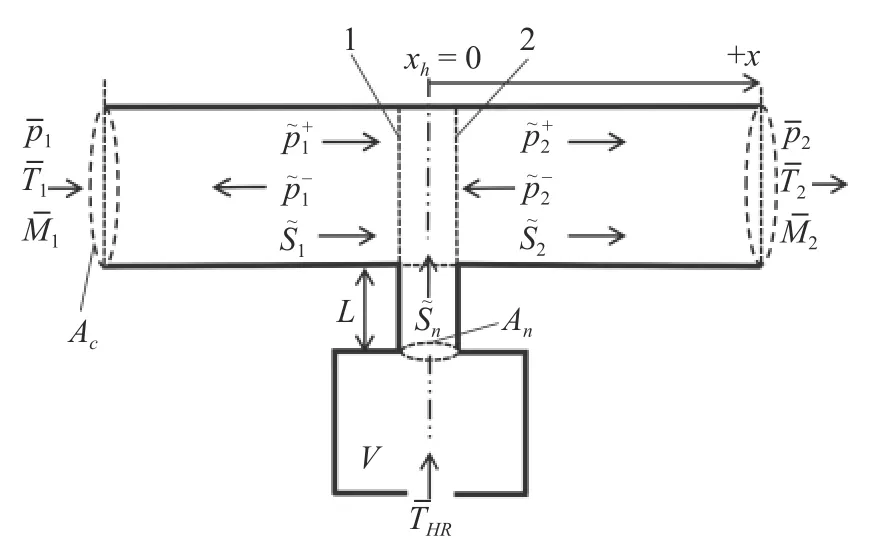
图1 安装有亥姆霍兹共振器的一维燃烧室管道Fig.1 A Helmholtz resonator installed in an combustor duct

图2 无限薄的积分控制体Fig.2 Infinitely thin integral control body
由于本文只研究带冷却气流的亥姆霍兹共振器对带有高温流体的燃烧室内声波的影响,不考虑燃烧室内的燃烧过程本身,故在分析过程中先做如下假设:假设系统中的介质为可视作理想气体的空气,符合理想气体方程p=ρRT,其中R为气体常数 ;无黏性耗散作用;忽略体积力、所有的热源和热扩散.
对该一维燃烧室管道应用质量、动量和能量守恒得到

式中,u为速度,为从HR 输入的质量流量源项,E˙为从HR 输入的能量流量源项,δ(x)为狄拉克 δ 函数用来规定质量源项和能量流量源项的输入位置为x=0.在燃烧室内沿着x方向上的动量是恒定的,因为在燃烧室中假定共振器颈流是径向向内的.
在图1 中取截面1-1和截面2-2 之间为控制体,并假设截面1-1 到截面2-2 的距离 dx无限小,如图2所示.将式(1)对x从1-1 截面到2-2 截面积分得到
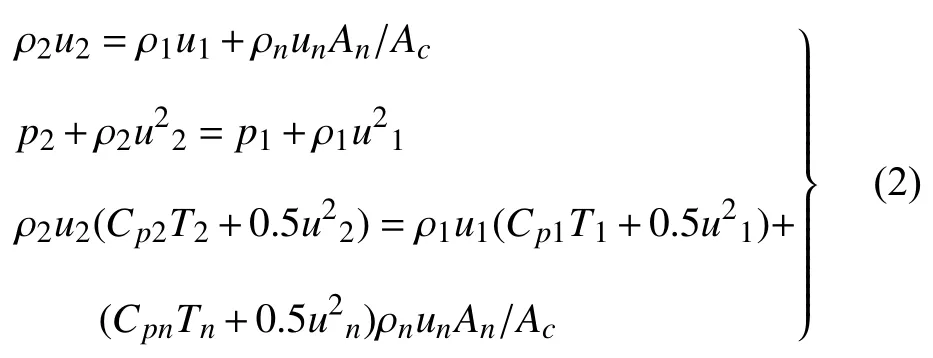
式中,Cp为定压比热容.式(2)等价于
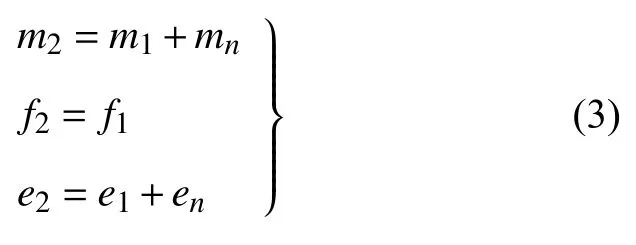
式中,m,f和e分别表示质量,动量和能量流量
为了得到共振器上下游平均量的关系,对式(2)取平均量得

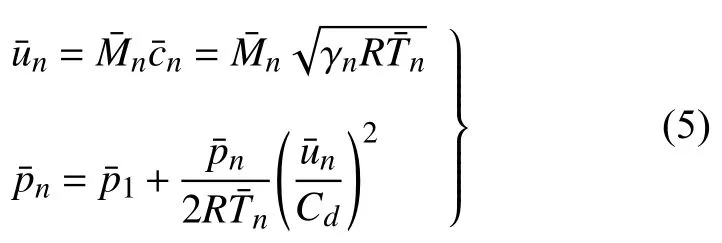
HR 的平均质量通量通常比燃烧室内的平均质量通量要小得多,因此燃烧室的平均流量在经过HR 后变化很小.在计算方程(5)时,考虑所以共振器上下游平均量几乎相等,这一点从上面的计算中也可以得到.但在后续计算中,如无特别说明,使用的平均量为方程(4)的解,故使用下角标1,2 以作区分.
对方程(1)中质量和动量守恒方程做线性化,即将所有流动量表示为一个平均量和一个扰动量的和,代入原方程,忽略二阶及高阶扰动项,可以推导出线性化的质量和动量方程为
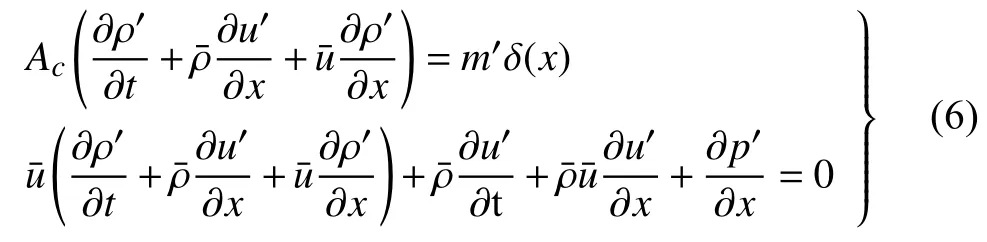
为了得到方程(6),假设了所有平均流量参数是沿空间是均匀(或变化缓慢),即
由于系统中存在冷热流量动态掺混,为非等熵过程,根据能量方程可知,系统自然会产生熵波.因此,温度扰动将包含熵扰动的影响,其推导可由能量方程给出.通过热力学关系可以得出密度扰动与压力扰动和熵波扰动的关系式为
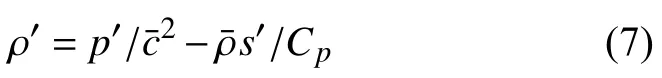
式中,s′为熵扰动,第一项是由声波扰动带来的影响,第二项是由熵波扰动带来的影响.
将非等熵过程的密度扰动表达式(7)代入到线性化的质量和动量方程(6)来引入熵扰动的影响,可以得到带源项的一维波动方程
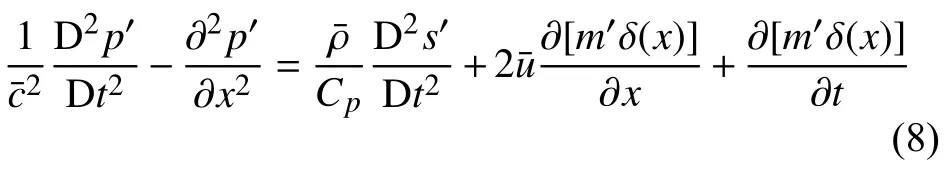
式中,D/Dt=∂/∂t+/∂x为物质导数.该方程具有声类比的形式——等式左边为描述声传播的波动方程,等式右边包含由熵扰动和HR 质量扰动引起的声源[20].显然,熵扰动的产生将会影响声波方程.可以看出,HR 的引入会给燃烧室带来一个质量扰动源,该质量扰动通过方程(8)右边的后两项来影响燃烧室内的声波.与此同时,HR 的存在还可能导致燃烧室内熵扰动的产生.这种方式产生的熵扰动通过方程(8)右边的第一项也可以影响燃烧室内的声波[21].而熵扰动具体如何影响声波方程可通过后面推导得出的声类比模型方程分析得出.
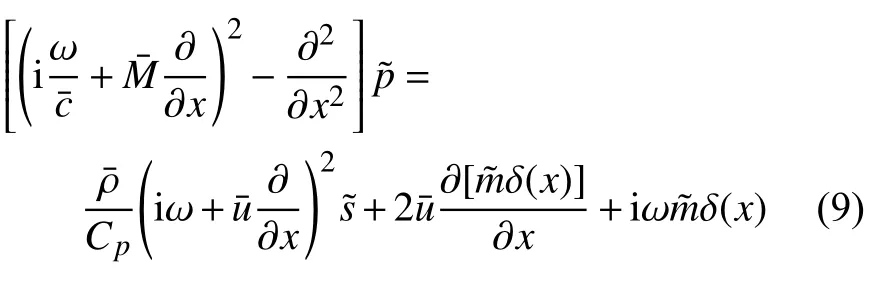
1.2 亥姆霍兹共振器模型
方程(9)右边的质量扰动来源于共振器颈部的质量扰动,其计算可通过共振器模型与共振器入口的压力扰动的关联得出.在共振器颈部有平均颈流(也叫做偏流)的情况下,入射声扰动将导致颈部穿孔边缘非定常的涡脱落,脱落后被颈部的平均流带走,并最终通过黏性效应耗散为流体的内能[16].穿孔颈部的声吸收特征由瑞利导率决定[22],定义为
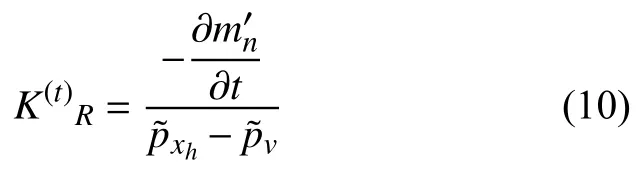

式中,I1,K1分别为第一类和第二类修正贝塞尔函数,为颈部的斯特劳哈尔数,rn为颈部截面的半径,为颈部的涡对流速度,根据文献[11,22-23],颈部的涡对流速度近似等于颈部的平均速度.
对于HR 空腔,质量守恒可以得到

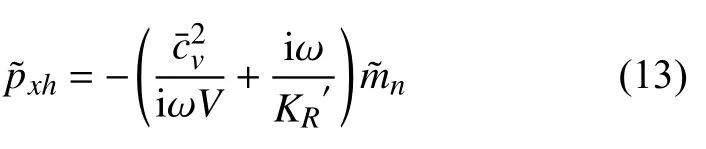
式中,V为HR 空腔体积,为空腔中的平均声速,ω为角频率,为总的瑞利导率,由于HR 颈部内外的压差可近似地视为颈部流体的涡流脱落和流体在颈部加速的贡献的总和,从而颈部有限的几何长度会带来一个对瑞利导率的修正,修正后总的瑞利导率满足[11,24-26]

式中,L为HR 颈部的长度.
定义HR 颈部的声阻抗为[14]ZHR=,通过下式计算
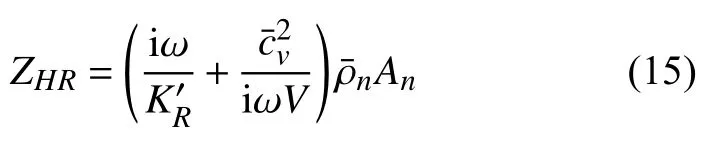
1.3 模型的解
求解频域下声类比模型方程(9)的解,对方程(9)来说:
(1)在x<0 段,质量扰动源为零,熵扰动也为零;
(2)在x>0 段,质量扰动源为零,方程右边第一项整体也为零.
所以在这两段,方程(9)右边源项都为零.对于这两段,通过转换到频域,偏微分方程转化为常微分方程.解得该方程通解为

式中,k+,k-为波数,由下式计算

在0-<x<0+段,质量扰动源不为零.对方程(9),从 0-到 0+对x分别作一次和二次积分.可以得到

式中t1,t2,λ1,λ2可由如下式子计算

式(19)中,所有平均量已经可以在前文中求出.而HR 质量扰动也可通过线性HR 声学模型与共振器出口压力扰动联系,即式(13).
为将熵扰动与HR 上、下游压力扰动关系式求出,对方程(2)中质量和能量守恒方程作线性化,忽略一阶以上的扰动,可以改写为
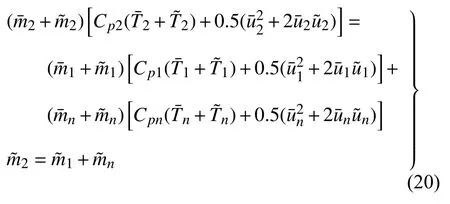
将式(20)改写,由此可以得到和其余变量之间的关系


式(21)中的可以用热力学关系式计算


对于燃烧室中HR 上游或者下游局部,可以通过线性化后的局部质量和动量守恒[13,16]
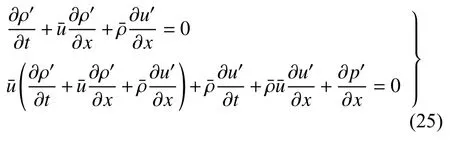
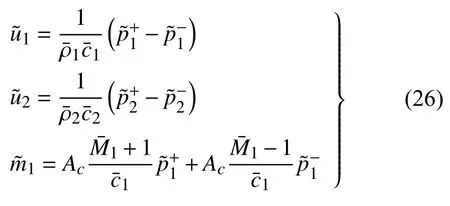
式(21)中,可用HR 的线性模型的声阻抗定义计算



其中

作量纲分析,t1,2中第一项与第三项的比为


将质量扰动表达式(13)代入式(18)中,可进一步减少未知数与方程组数量,得到
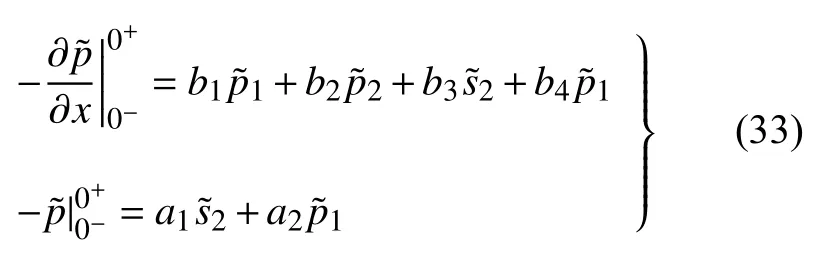
式中参数b1,b2,b3,b4,a1,a2如下
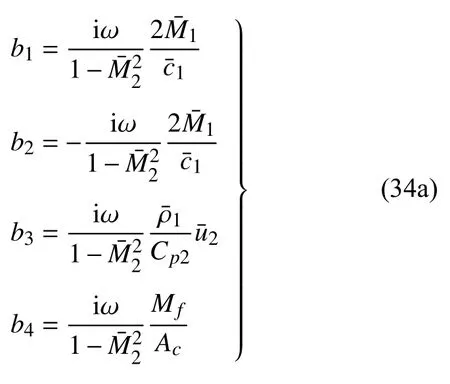
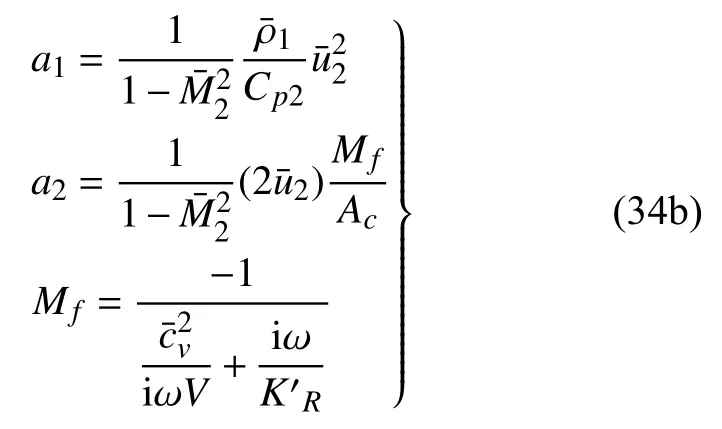
式(34)中,所有平均量已经可以在前文中求出.至此,只需联立式(29)和式(33)共3 个方程,其中包含等共5 个未知数.此方程组不闭合,无法求解,故需要加入边界条件.边界条件一般为HR 上、下游扰动幅值,中其中2 个.由于在实际应用中,往往将亥姆霍兹共振器安装在管道内声波模态波峰处,以达到最佳的消声效果,故本文中主要选取了该请况讨论(给定和).对于给定上游入射声波,并假设下游无入射声波=0的情况,在此提供下述初步分析结果.对于给定下游入射声波,并假设上游无入射声波的情况,可通过相同的方程代入该边界得到.上述后两种情况的线性组合可得到一般声波入射情况的解.如此未知数减少2 个,上述方程组闭合.联立上述3 个方程可以解得的表达式,并进而可求得所有相关未知量.


2 测试与验证
在本节中,用一个测试案列[16]来验证上述模型,并用这个案例来说明HR 与燃烧室的温度差是如何影响其吸声性能的.将圆柱形亥姆兹共振器安装于可视为一维管道的燃烧室上,如图1 所示.测试案例中HR和燃烧室的几何和平均流参数如表1 所示.由于模拟对象是HR 与燃烧室内局部(HR 上下游之间)的声波和熵波关系,故不需要规定燃烧室声学边界条件或HR 轴向位置[16].但在本节中假设 HR 安装在压力波腹附近以清楚地显示其对燃烧室声学的影响[9,27].实际中以给定入射波,假定边界无限长或者无反射的情况更具一般性,本文暂不考虑.

表1 HR和燃烧室的几何与平均流参数Table 1 Geometry and mean flow parameters of the HR and combustor
2.1 等温工况
通过方程f=c/(2π)可预测出HR 在1000 K 时的共振频率约为535 Hz.情况一,假设HR 上游的压力扰动幅值=100 Pa .定义熵波扰动强度幅值为,单位为Pa.其中,为熵扰动,量纲为J/(K·kg).通过所建模型绘制HR 下游压力扰动幅值以及下游熵波扰动等关键参数,并对比Yang 等[16]中的假设滞止焓连续的模型和阶跃条件模型的结果.如图3(a),在HR和燃烧室等温的情况下,在共振频率(约535 Hz)附近时,HR 的存在会显著影响燃烧室中共振器下游的声波强度,但是下游温度扰动保持不变,对共振器下游的熵波强度也基本没有影响.可看出文中提出的声类比模型能够很好地匹配另外两个模型[16]的结果.同时,这三个模型对HR 的声吸收系数也给出了一致的预测,如图3(c)所示.该声吸收系数的定义为吸收能量/入射能量[28-29]
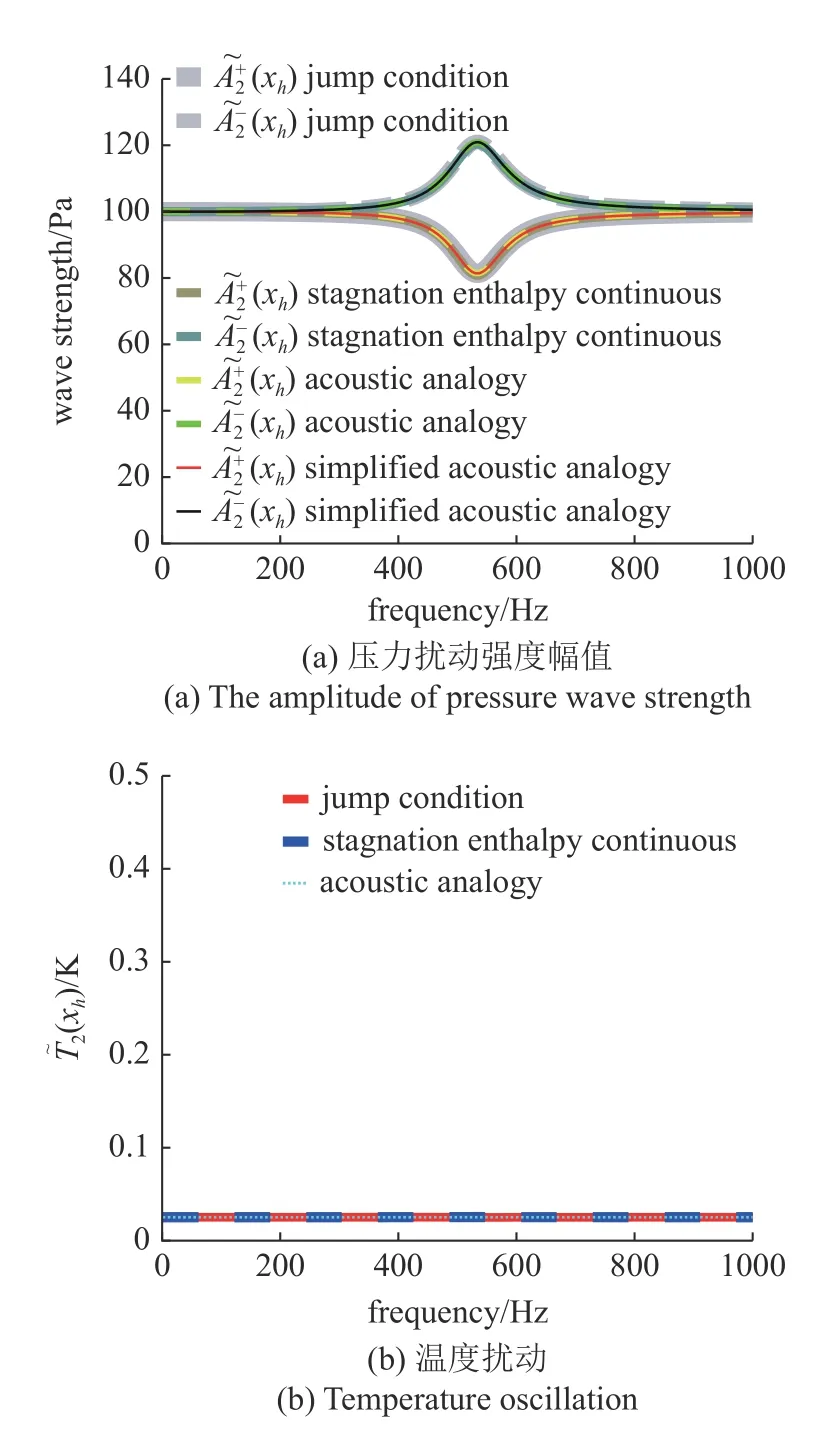
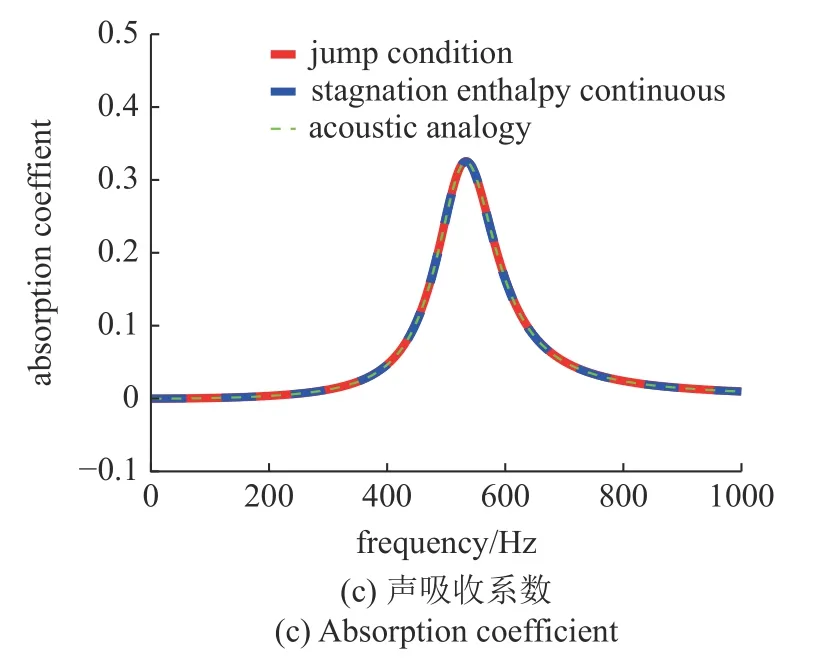
图3 HR 温度1000 K 时,3 个模型的压力扰动强度幅值、温度扰动和声吸收系数Fig.3 The amplitude of pressure wave strength,temperature oscillationt and absorption coefficien of the three models with a HR temperature of 1000 K
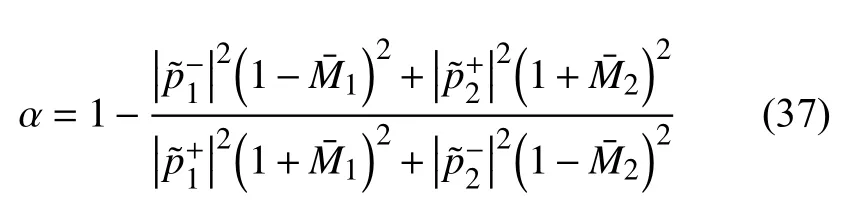
2.2 不等温工况
在HR和燃烧室不等温的工况下.设HR 空腔冷却气流温度从500 K 逐渐上升至1000 K,让HR和燃烧室(1000 K)温差逐渐变小,这时由于通过HR 的冷空气流产生的扰动,HR 下游熵波强度不再约等于零.采用和等温工况一样的假设:=100 Pa .
通过方程f=c/(2π)可预测出HR 在500 K 时的共振频率约为385 Hz.如图4(a)(b)所示,500 K 时声类比模型的对HR 下游温度,压力和熵波扰动强度的预测结果都与阶跃条件模型的预测结果完全一致.在共振频率(385 Hz)附近共振器下游会产生较强的熵波,而远离共振频率熵波强度明显下降.HR 下游的温度扰动也呈现出和熵波扰动一样的趋势,因为熵波扰动依赖于下游温度扰动和压力扰动.但当冷却气流温度从500 K 逐渐上升至1000 K 时,阶跃模型与声类比模型的熵波扰动共振幅值将逐渐减小,直到与滞止焓模型趋于一致(趋于0).而滞止焓连续模型在任何温度下都无法考虑HR 下游的熵扰动,故预测结果存在明显问题.除了在经过HR 后产生熵波外,HR 的较低温度也会导致HR 之前和之后的声波强度之间的关系发生变化,这点可以从模型的解,图4(a)中看出.虽然这3 个模型都预测出HR 的存在会导致向上游传播的声波强度加强,向下游传播的声波强度减弱[30-31],但声类比模型预测的变化趋势和要小于滞止焓模型,这与阶跃条件模型结果一致,而冷却气流温度从500 K 逐渐上升至1000 K 过程中,该结论任然成立.如图4(c)所示,500 K 时声类比模型预测的声吸收系数的变化趋势和峰值也要比滞止焓模型小(吸声系数相差约100%),跟阶跃条件模型一致.但当冷却气流温度从500 K 逐渐上升至1000 K 时,该差异逐渐消失.由于在实际燃气轮机和航空发动机中,总冷却气流可占到发动机空气总流量的20%或以上.而此处考虑的流过共振器的平均空气质量流量远小于燃烧室内平均空气流量,≈0.23% .但在共振频率附近,共振器颈部质量流量扰动幅值与燃烧室质量流量扰动幅值为同一数量级≈26.5%,(若前者远小于后者,则共振器无法产生显著消声效果).

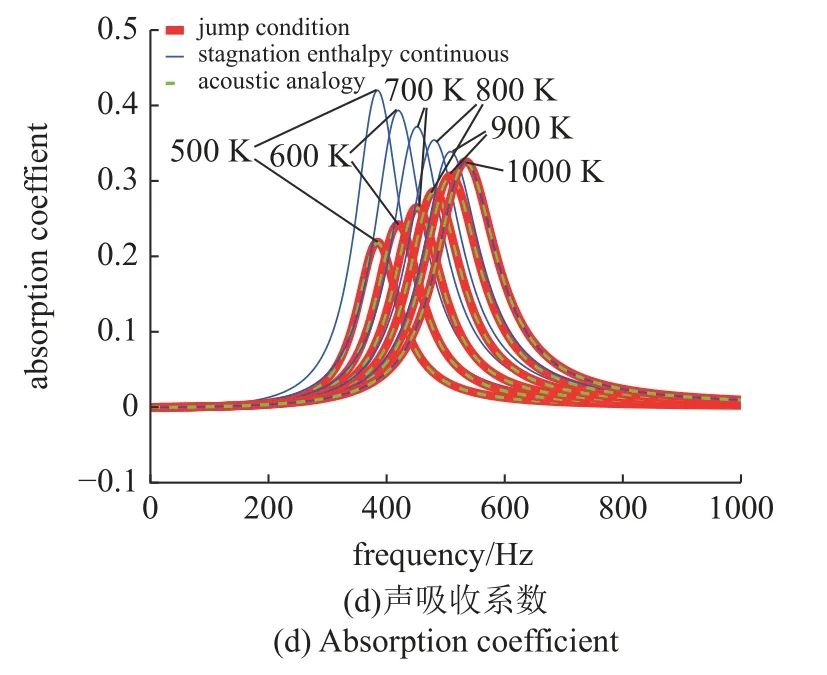
图43 个模型的压力扰动强度幅值、熵波扰动强度幅值、温度扰动和声吸收系数Fig.4 The amplitude of pressure wave strength,enthalpy wave strength,absorption coefficient and temperature oscillation of the three models
3 结论
当带有冷却气流的HR 被安装在一维管道燃烧室上时,燃烧室中热气流和HR 中冷气流的温差需要被考虑,这将改变燃烧室内共振器上下游的声波与熵波之间的关系,对HR 的吸声性能和HR 对热声振荡的抑制作用有显著影响——不同的声波关系改变了HR 的吸声性能,而产生的熵波如果在下游被加速,则可能导致熵噪声形式的声波.文献[16]基于阶跃条件模型得到了HR 上、下游的声波与熵波的关联,可以由上游声波与熵波代入所推导出的关系矩阵直接计算出下游的声波与熵波,但无法看出熵波产生以及声波关系改变的机理.本文推导了安装有带冷却气流的HR 的燃烧室中的声类比形式的声学模型.通过与阶跃条件模型的定量比较,验证了该声类比模型的正确性.本模型的优点在于它是带有源项的波动方程,从中可以直观地看到熵扰动声源项与共振器质量扰动声源项的表达式,能够区分出由熵扰动引起的声源项和声扰动引起的声源项.这为理解和预测带冷却气流的亥姆霍兹共振器对燃烧室热声振荡的影响提供了便捷的模型.
附录
方程组(28)和式(32) 3 个方程的求解

将上述方程组改写成

可解得


