The characteristics of spontaneous near-inertial wave generation from an anticyclonic mesoscale eddy*

Bo ZHAO , Zhenhua XU , Qun LI , Wenjia MIN , Yang WANG ,Baoshu YIN 1, 2, 3, 4, 5

1 CAS Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology Chinese Academy of Sciences, Qingdao 266071,China

2 Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China

3 Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China

4 College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

5 CAS Engineering Laboratory for Marine Ranching, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071,China

6 Polar Research Institute of China, Shanghai 200136, China

Abstract The generation and propagation characteristics of near-inertial waves (NIWs) generated spontaneously from a quasi-geostrophic anticyclonic mesoscale eddy in a rotating and stratif ied f luid were investigated by three-dimensional numerical modeling. NIWs are generated over a long time interval as a forced response to balanced baroclinic mesoscale eddies. For such eddies, NIW generation from balanced f low is an inevitable result as the evolution of eddies. Moreover, the baroclinicity of mesoscale eddies is an essential condition for this NIW generation mechanism. The spontaneously generated NIWs radiate horizontally toward the eddy center and propagate upward in vertical direction. The forcing of the NIWs moves downward along the eddy axis from the location of maximum temperature anomaly of the mesoscale eddy. The moving speed of the forcing is independent on the balanced mesoscale eddies but is determined by the ratio of buoyancy to inertial frequency. When the forcing reaches the bottom of the mesoscale eddy, the spontaneous NIW generation process terminates. NIW intensity in this spontaneous generation process is strengthened with the increase of the Rossby and Froude numbers. Further research to gain a solid understanding of the role of the Rossby and Froude numbers is necessary for the parameterization of spontaneous NIW generation from quasi-geostrophic mesoscale eddies in general circulation model.

Keyword: near-inertial waves (NIWs); anticyclonic mesoscale eddy; spontaneous generation

1 INTRODUCTION

The ultimate fate of multi-scale oceanic energy is its microscale dissipation. However, as the huge kinetic energy reservoir, mesoscale eddies transfer upscale much more energy than cascade downscale(Scott and Wang, 2005). Therefore, mechanisms must exist that drain energy from mesoscale eddies and to arrest their inverse cascade. One candidate for such a mechanism is the connection to internal waves,including the interactions between internal wave f ield and background f lows, and internal wave generation in the loss of balance process (Ferrari and Wunsch,2009). The internal wave f ield is also regarded as one of the main potential energy contributors to diapycnal mixing, which is important in determining the oceanic general circulation, in the ocean interior (Wunsch andFerrari, 2004). Loss of balance and the subsequent inertial-gravity wave (IGW) generation mechanisms have been investigated in theory and numerical modeling (McWilliams and Yavneh, 1998; Molemaker et al., 2005; Aspden and Vanneste, 2009; Nagai et al.,2015; Zhao et al., 2021a). Alford et al. (2013)conjecture that near-inertial waves (NIWs) observed near the North Pacif ic Subtropical Front are generated spontaneously from the front. Nevertheless, the detailed behaviors of the spontaneously generated internal waves when the balance of f lows is broken,remain obscure.

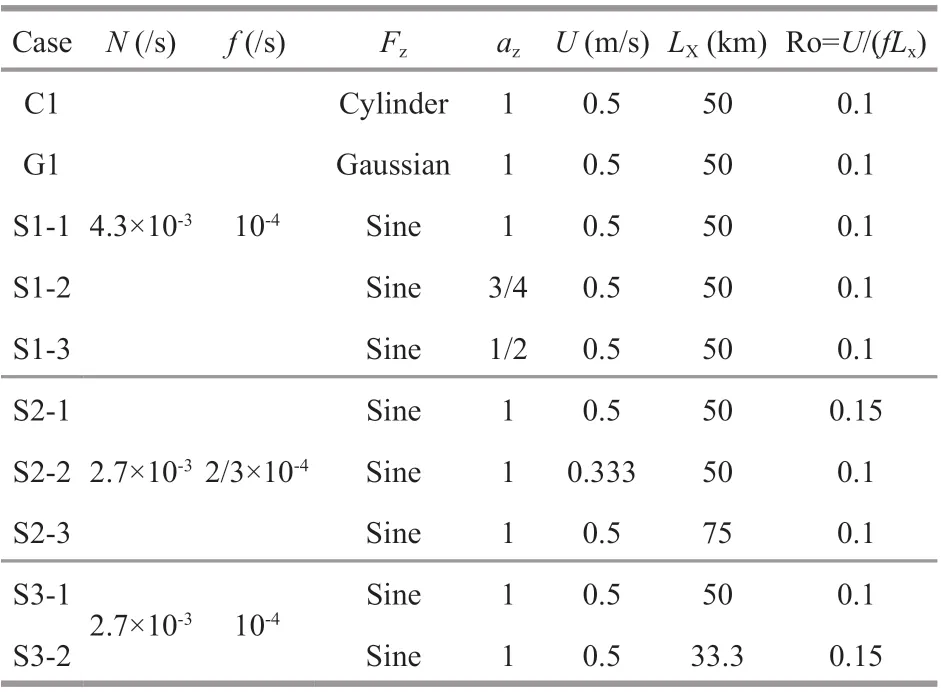
Table 1 Parameters of the numerical simulations

The timescale separation between slow balanced f lows and fast IGWs is an essential characteristic of mid-latitude ocean mesoscale dynamics (Vanneste,2013). In other words, balance f lows are invariant in the IGW timescale, and the balance model f iltered IGWs out can be used to approximate the mesoscale dynamics. Exactly balanced f lows inevitably radiate IGWs via spontaneous generation mechanism (Warn et al., 1995). Therefore, f lows evolving over much longer timescales than the period of IGWs are regarded as a fuzzy slow manifold in the space state of primitive equations and act as the sources of IGWs(Warn, 1997). In particular, spontaneous generation mechanisms are quite diff erent for the hydrostatic,geostrophic, and quasi-geostrophic f lows (Ford, 1994;Vanneste and Yavneh, 2004; Snyder et al., 2007).

For vortex trains with Froude number Fr＜＜1 and Rossby number Ro～1, Ford (1994) extended the Lighthill theory of aerodynamic sound generation in a shallow water system. Spiral gravity waves are radiated from the vortex to the far f ield by the forcing terms, which are assumed non-zero spanning a small region and can be approximated as a quadrupole point in the Lighthill-Ford theory (Sugimoto et al., 2015).For geostrophic f low, instability associated with singularity structure of balanced motions occurs and IGWs are emitted. Similar to the case of small Froude number limit f lows, spiral waves arise as a result of the evolution of an axisymmetric geostrophic vortex(Lelong et al., 2020) and the merging of two baroclinic anticyclones (Pallàs-Sanz and Viúdez, 2008). Vanneste and Yavneh (2004) suggested that IGW intensity strengthens exponentially with the Rossby number.

A quasi-geostrophic dipole vortex in the atmosphere was simulated by Snyder et al. (2007) and the associated spontaneous IGW generation was described. The waves generated spontaneously by the dipole are upward-propagating with a near-inertial intrinsic frequency. One specif ic characteristic of this wave generation is that the waves are embedded within and stationary relative to the propagating dipole. This provides the evidence that the IGWs result from a forced linear response to balanced f low(Snyder et al., 2009). However, although the Lighthill-Ford theory is expected to be extended in the small Rossby number limit, an accurate spontaneous generation theory for quasi-geostrophic f lows does not exist yet. In order to explain the spontaneous IGW generation mechanism, we investigate the quasigeostrophic balance broken process and the accompanying IGWs numerically.In the present study, a suite of mesoscale eddies with diff erent vertical structures, as well as background stratif ications and local inertial frequencies, are simulated and compared in the f plane. This paper is organized as follows. In Section 2, the method and conf igurations of the numerical model are explained and the diff erent cases summarized. Section 3 describes the results from the numerical model of the generation process of NIWs and explores the factors inf luencing of the NIW intensity in this process.Section 4 presents a discussion and Section 5 summarizes the results.

2 METHOD

The Massachusetts Institute of Technology general circulation model (MITgcm) was used to solve the nonlinear primitive equations with hydrostatic balance in the vertical direction. Diff erent vertical eddy structures, horizontal velocities, as well as background stratif ications and local inertial frequencies, are simulated in the f-plane, as summarized in Table 1. Another critical dimensionless parameter in the simulation of mesoscale eddy is the Rossby number,

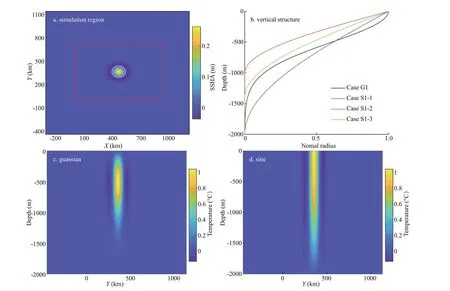
Fig.1 The initial conditions and conf iguration of the numerical model

wherefis the Coriolis parameter,UandLxare characteristic velocity and length of mesoscale eddies,respectively. The anticyclonic eddy maintains its initial location throughout the simulation, rather than propagating southwestward due to beta eff ect and nonlinearity of eddy (Chelton et al., 2011; Early et al.,2011; Hao et al., 2021). The vertical eddy velocity f ields and temperature anomaly, including sinusoidal and Gaussian functions, are shown in Fig.1.Additionally, a barotropic cylinder eddy is simulated to study the importance of baroclinicity.

All cases have the same simulation domain and resolutions. The simulation domain constitutes a higher resolution domain and a stretched domain. The gridding outside the nested domain is stretched from 6 km×6 km to 25 km×30 km. The horizontal resolution of the nested domain is Δx=Δy=5 km. The stretched grid domain is set to minimize the inf luence of complicated signals ref lected by the boundaries. The total and the inner nested domains are 1 515 km×1 580 km and 920 km×710 km, respectively. The depth is 2 km and the vertical resolution is Δz=40 m in the whole simulation domain. The anticyclonic geostrophic mesoscale eddies in all cases are set in the location (460 km, 355 km). The sea surface height anomaly (SSHA) is colored in Fig.1a. The zero contour of relative vorticity is represented by a white circle.

The normalized SSHA of an eddy is set as a Gaussian function (Wang et al., 2003; Zhang et al.,2013; Hou et al., 2019; Xu et al., 2020)

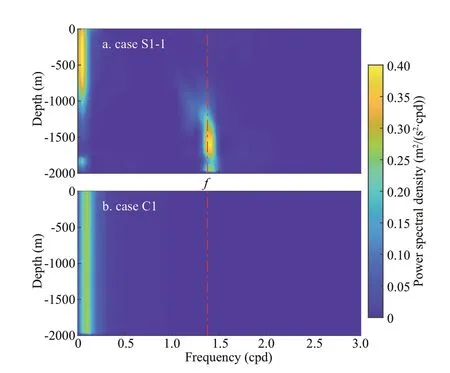
Fig.2 Frequency-depth plot of the horizontal kinetic energy at position (520 km, 440 km), inside the eddy

The horizontal velocity f ield is obtained via geostrophic relationship from the Gaussian SSHA function. The salinity is set as a constant 35, and the saline expansion coeffi cient is zero. Therefore, the density gradient is determined only by the temperature structure as shown in the approximation of state equation:

whereTrefis the reference temperature with vertically linear and horizontally uniform distribution,αT=2×10-4/K is the constant thermal expansion coeffi cient,and the density perturbation,ρ, is gained by hydrostatic balance after determining SSHA (Hyun and Hogan, 2008; Yang et al., 2017). The linear temperature distribution and the zero saline expansion coeffi cient yield the linear buoyancy frequency.

3 RESULT

3.1 Spontaneous NIW generation process

In the initial stage of the model, the geostrophic balance eddy, as exactly invariant slow manifolds,inevitably radiates spiral IGWs toward the far f ield before the 4thday, as predicted by the transient generation mechanism. After this adjustment process is terminated, the vortex can be regarded as a quasigeostrophic f low, which generates waves with specif ic characteristics. Snyder et al. (2009) suggested that IGWs are generated as a forced linear response to the quasi-geostrophic dipole.

As Table 1 shown, the mesoscale eddy is baroclinic in case S1-1. In this case, a frequency-depth plot(Fig.2a) for the horizontal kinetic energy at position(520 km, 440 km), inside the eddy, shows that the NIWs dominate the energy of internal wave continuum. Because of the huge kinetic energy,mesoscale eddies are regarded as eff ective sources of NIWs. A similar frequency-depth plot for case C1, in which the eddy is barotropic, is shown in Fig.2b.There is no high-frequency motion generated from the barotropic low-frequency f low. Therefore, we suggest that the baroclinicity of an eddy is essential for the spontaneous NIW generation. Based on this characteristic, it is conjectured that the forcing terms are only constituted by the vertical shear of the mesoscale eddy. For mesoscale eddies, higher baroclinic mode energy is collected in the f irst mode and f inally transfers to barotropic mode; thus, the energy is dominated by the f irst baroclinic and barotropic modes (Smith and Vallis, 2001). Theories of nonlinear geostrophic turbulence show that the forward energy cascade to smaller scales is forbidden and the barotropic kinetic energy cascades inversely(i.e., upscale) at scales larger than the corresponding Rossby deformation radius (Charney, 1971; Haidvogel and Held, 1980). Unbalanced NIWs cascade their energy inevitably to the molecular scale and are major contributors to diapycnal mixing due to their strong vertical shear (Garrett, 2001; Alford et al., 2016).Hence, spontaneous NIW generation process can be regarded as a pathway of baroclinic eddy energy downward cascade, as well as eff ective energy sources to diapycnal mixing (Watson, 1985; Bühler and McIntyre, 2005).

We now analyze the spatial structure of the NIWs.The horizontal divergence (HD) can be used to identify the waves, because the horizontal divergence is approximately zero for the eddy while it is non-zero for IGWs (Danioux et al., 2012). In addition, by usingL/Uto nondimensionalizet, Warn et al. (1995) showed that the primitive equations can be rewritten as

Selecting a horizontal section at 360-m depth as an example, Fig.3 illustrates the IGWs on the 4th, 6th, 8th,and 10thdays. The IGWs remain within the range of the mesoscale eddy, rather than radiating toward the far f ield; and the patterns of IGWs are concentric circles centered at the eddy center. Furthermore, the closer to the center, the longer wavelengths. From the dispersion relation, the waves propagate toward the eddy center in the horizontal direction.

In cases S1-1 and G1, the vertical structure of mesoscale eddies are set as sinusoidal and Gaussian functions, respectively. The vertical section of the horizontal divergence f ield in these two cases alongX=460 km (the diameter of the eddy) is shown in Fig.4. The waves have the same symmetry axis and slope as the eddy. On the symmetry axis, NIWs are strengthened due to their nonlinear interactions. The NIWs are conf ined in the zero pressure contours,represented by the black lines in Fig.4a, b, & c, in the initial NIW generation stage. When NIWs propagate into an anticyclonic mesoscale eddy, the eff ective Coriolis frequency decreases because of the negative relative vorticity of the eddy, and the vertical wavelengths of the NIWs decrease (Kunze, 1985).This results in a sharp increase in the vertical phase speed, and the NIWs are drained to depth along the anticyclonic eddy (Zhai et al., 2005). The NIWs generated from the subsurface eddy (G1) have broken through the zero pressure contours on the 8thday without any change in their slopes and vertical wavelengths. Therefore, the conf inement of the NIWs is due to their forcing located inside the eddy rather than due to the chimney eff ect of an anticyclonic mesoscale eddy.

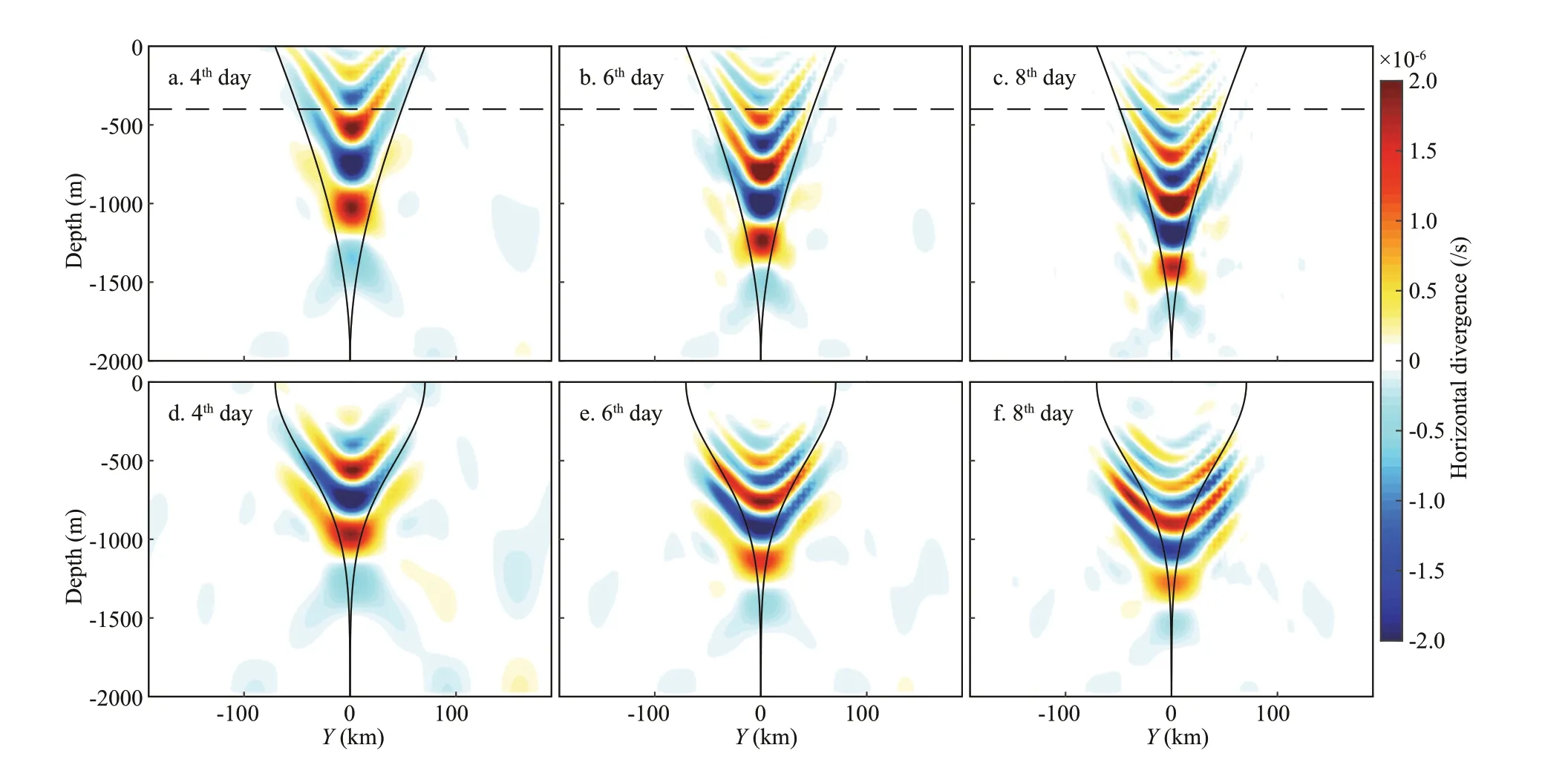
Fig.4 Vertical section of horizontal divergence along the eddy diameter X=460 km

In cases S1-1, S1-2, S1-3, the vertical structures of mesoscale eddies are set as sinusoidal functions with diff erent semi-axis while the mesoscale eddy in case G1 has a Gaussian vertical structure function. A time series of the horizontal divergence for these cases at the eddy center is shown in Fig.5. Notably, NIW patterns move downward (Fig.4), but the phases propagate upward (Fig.5). In addition, as Fig.5 shows,the timescale of downward moving is approximately estimated of 10 days, which are much longer than near-inertial period. Hence, the NIW patterns, as shown in Fig.4, are formed by the local spontaneous generation rather than by their free propagation after generation. The forcing determines the locations of spontaneous generation, which moves downward along the eddy axis. As with all IGWs, the group velocity is perpendicular to the phase velocity, so that the near-inertial energy transferred from the eddy propagates downward for the entire run-time of the simulation.

Comparing eddies with diff erent vertical semi-axis shows that the spontaneous generation does not always occur in the simulation. Spontaneous NIW generation terminates when the forcing moves to the bottom of the eddy, as marked by the dashed lines in Fig.5b & d. The movement of forcing is tracked using the location of maximum horizontal divergence at the eddy center, as shown in Fig.6. For the subsurface mesoscale eddy (case G1), NIWs are generated spontaneously at approximately 500-m depth at the beginning of the simulation (Fig.6). While, in the surface eddy cases (S1-1, S1-2, S1-3), the maximum horizontal divergence locates at sea surface in the initial moment of simulations (Fig.6). The spontaneous generation process starts at the location of maximum temperature anomaly (Fig.1) and terminates when forcing reaches the bottom of the eddy. After generation terminates, NIWs propagate freely and ultimately dissipate.Near-inertial waves are generated spontaneously as a forced response to a baroclinic mesoscale eddy.The forcing moves from the location of maximum temperature anomaly to the bottom of the eddy. This results in the NIW patterns being conf ined within the eddy, moving downward despite the upward phase propagation of the waves. In next section, NIW intensity is studied by comparing cases with diff erent background parameters.

3.2 Factors inf luencing NIW intensity

We now examine the factors that inf luence NIW intensity. The spontaneous generation mechanism is the unique wave generation manner of a rotating f luid.Hence, the Coriolis parameterf, which is used to estimate the rotation speed of the earth, is an essential factor in the spontaneous IGW generation. The baroclinicity of a mesoscale eddy is essential for the NIW generation, as the contrast between two eddies—one with a sinusoidal vertical structure and one with a cylindrical vertical structure—as discussed in the above section. Hence, the inf luence of the vertical shear of the horizontal velocity of eddy is examined in this section. Similarly, other eddy parameters,including initial horizontal velocity and radius, are compared with one another. Moreover, the internal waves can be regarded as the perturbation of an isopycnic surface; hence, the stratif ication parameterNsignif icantly inf luences factor on internal wave intensity. In this section, we examine the inf luence of these factors on the intensity of NIWs generated spontaneously.

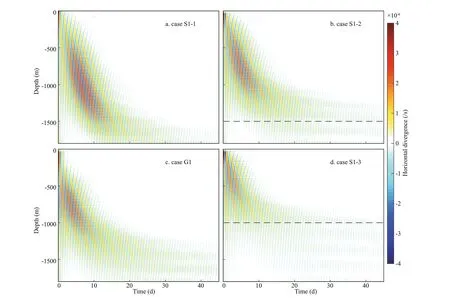
Fig.5 Time series of horizontal divergence at the eddy center

3.2.1 Eff ect of stratif ication

The conversion rates for both barotropic tides and large-scale geostrophic f lows to internal waves are positively related with buoyancy frequency (e.g. Bell,1975; Smith and Young, 2002; Xu et al., 2013, 2014,2016, 2021; Wang et al., 2018; Chang et al., 2019;Zhao et al., 2021b). The inf luence of stratif ication on spontaneous NIW generation is studied by comparing cases S1-1 (N=4.3×10-3/s) and S3-1 (N=2.7×10-3/s).Table 1 shows that these two cases have the same eddy parameters but diff erent buoyancy frequencies.The frequency-depth spectra of vertical velocities,which are horizontally spatial averaged, for cases S1-1, S3-1, and S2-1, for the whole run-time of the simulation are shown in Fig.7. The near-inertial energy in case S3-1 is more than in case S1-1.Therefore, in contrast with internal waves generated by other mechanisms, weak stratif ication results in increased energy transfer from mesoscale eddies to NIWs via the spontaneous generation mechanism.Additionally, an indicator is def ined as the horizontal integration of the square of the horizontal divergence over the whole simulation domain:

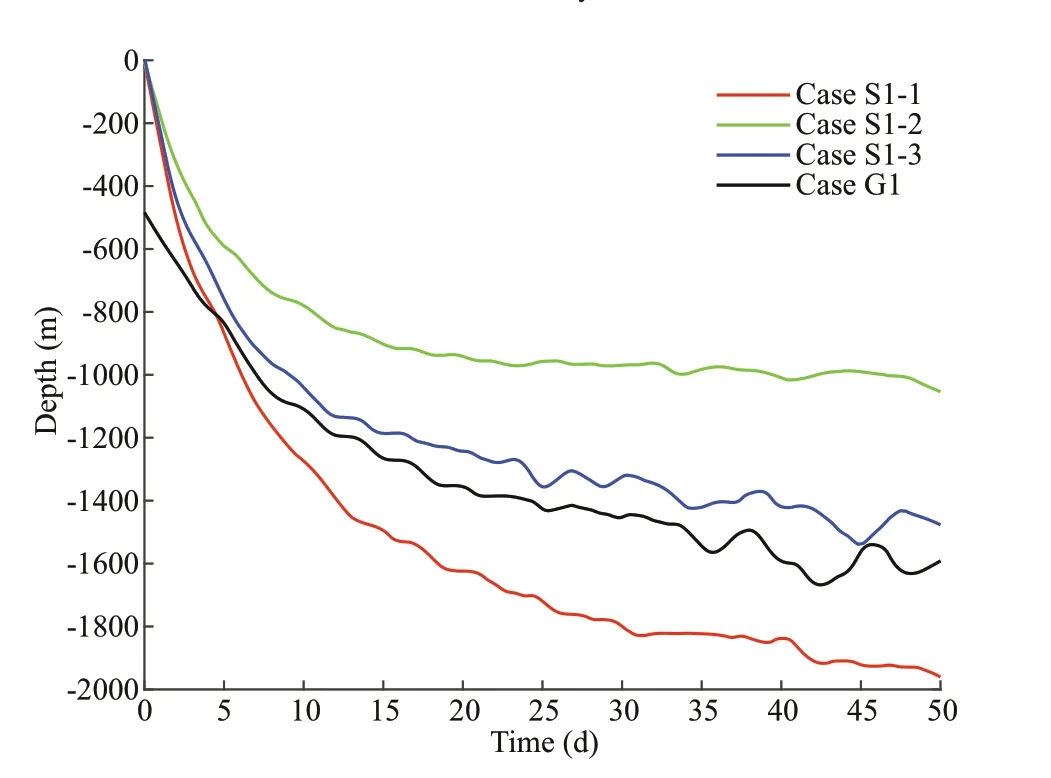
Fig.6 Time series of the maximum horizontal divergence location for cases S1-1, S1-2, S1-3, and G1

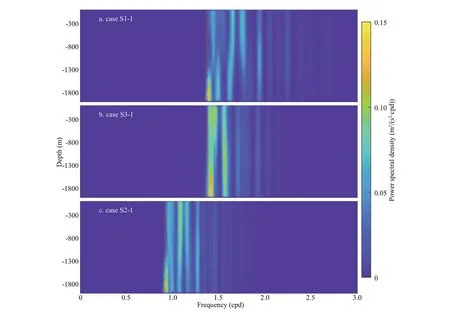
Fig.7 Frequency-depth spectra of horizontally averaged vertical velocity for the total simulation run-time

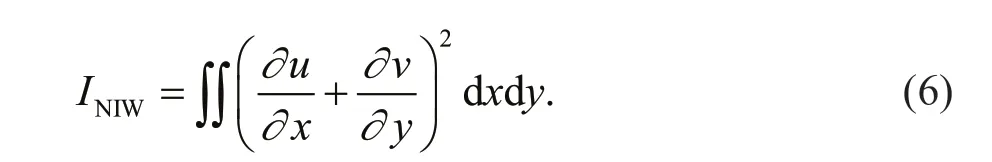
It has the same dimensionality as energy and can be used to estimate the intensity of fast unbalance waves generated spontaneously from slow balanced f lows. Time series of this indicator in diff erent cases are plotted in Fig.8 to compare NIW intensity (INIW).Figure 8a & c show that the stronger background stratif ication, NIWs generated spontaneously are much more active.

3.2.2 Eff ect of inertial frequency

In cases S3-1 and S2-1, all the parameters are the same, except for the local inertial frequencies, which are 10-4/s and 6.667×10-5/s, respectively. Figure 7b &c show that the energy is distributed over a wide range of the internal wave frequency band, with the largest proportion concentrated near the local inertial frequency. The near-inertial energy is immediately transferred from the eddy, and the higher frequency energy is from the nonlinear interaction among NIWs(Li et al., 2018). There is only a small diff erence in NIW kinetic energy in these two cases (Fig.7b & c)whileINIWin case S2-1 (Fig.8b) is obviously larger than that in case S3-1 (Fig.8c). Therefore, we propose that NIW potential energy is more sensitive to inertial frequency than wave kinetic energy, and that NIW intensity negatively correlates with local inertial frequency.

3.2.3 Eff ect of eddy vertical semi-axis

The necessity of mesoscale eddy baroclinicity for the generation of NIWs has been demonstrated in Section 3.1. Unless background f low features velocity shear, the energy transformation between f low and internal waves could occur, including wave capture(Bühler and McIntyre, 2005; Kelly et al., 2016; Jing et al., 2018) and some instability mechanisms. Table 1 shows Gaussian and sinusoidal functions, with diff erent vertical semi-axis, for cases S1-1, S1-2, and S1-3.INIWincreases as the vertical range decreases, as shown in Fig.9a & b. More intuitively, the vertical averages ofINIWfor these cases are plotted in Fig.10a,and the normalized vertical shear of the eddy horizontal velocity is shown in Fig.10b. A stronger vertical shear in eddy horizontal velocity results in more energy of NIWs generated spontaneously, as shown in Fig.10.

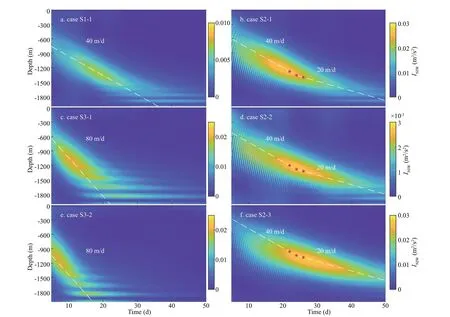
Fig.8 NIW intensity

Fig.9 As per the Fig.8, but for cases S1-3 and S1-2

3.2.4 Eff ect of eddy horizontal velocity

We set the initial surface horizontal velocity of the mesoscale eddy to 0.5 m/s and 0.333 m/s for cases S2-1 and S2-2, respectively. Figure 8b & d show that the larger the initial horizontal velocity of the mesoscale eddy, the stronger the NIW intensity.Moreover, although the initial horizontal velocity in case S2-2 is two thirds of that in case S2-1, the NIWs in case S2-1 are an order of magnitude larger than those in case S2-2. In contrast, the diff erences of eddy semi-axis, buoyancy, and inertial frequency in the contrast cases are all roughly two thirds, and the NIW intensities are of the same order. Therefore, we propose that the correlation between the eddy horizontal velocity and NIWs generated spontaneously from the eddy is not linear.

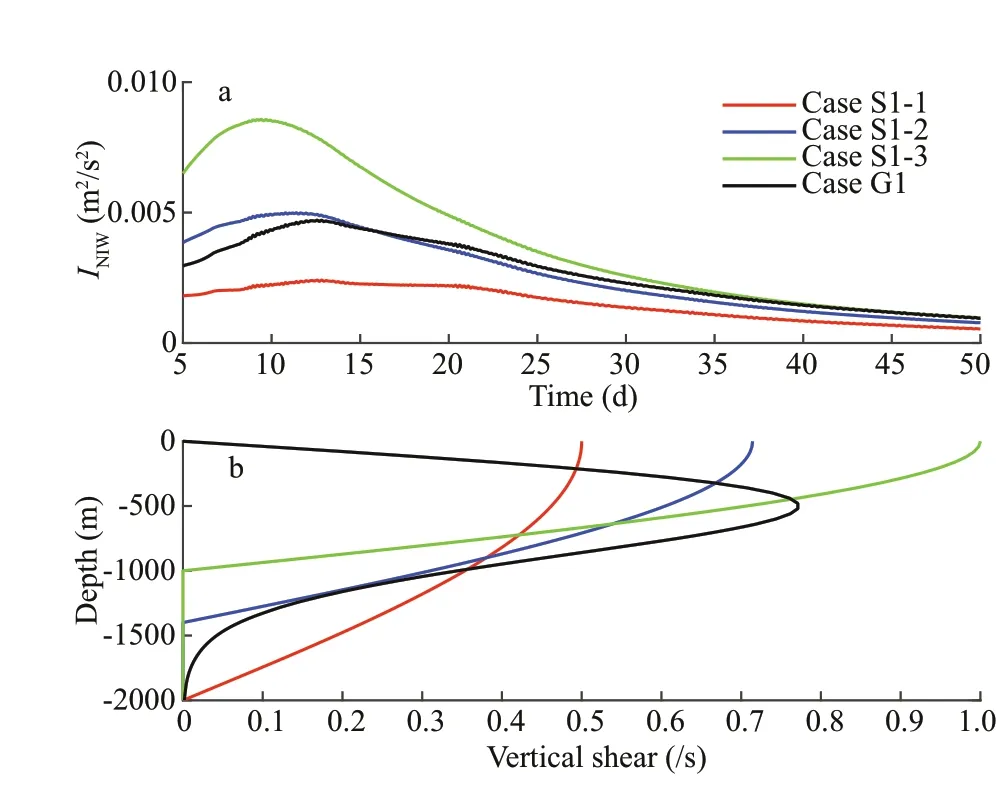
Fig.10 Vertical average of NIW intensity for cases G1, S1-1,S1-2, and S1-3 (a) and the normalized vertical shear of eddy horizontal velocity (b)

3.2.5 Eff ect of eddy radius

In cases S2-1 and S2-3, the eddy radii are set to 50 km and 75 km, respectively. The maximum amplitudes of NIW horizontal divergence in these two cases are approximately the same, while the NIW generation period in case S2-3 is obviously longer than in case S2-1 (Fig.8b & f). Comparing the vertical averages of NIW intensity (INIW), a longer eddy radius results in only a slightly weaker NIW, as shown in Fig.11. This indicates that eddy radius has a relatively weak eff ect on NIW intensity compared to eddy horizontal velocity, semi-axis, buoyancy, and inertial frequency. However, as shown in Fig.11, a shorter radius of a mesoscale eddy results in earlier occurrence of spontaneous NIW generation, as the vertical averages ofINIWpeaks appear earlier in case S2-1(50-km radius) compared with case S2-3 (75-km radius), and earlier in case S3-2 (33.3-km radius)compared with case S3-1 (50-km radius) .

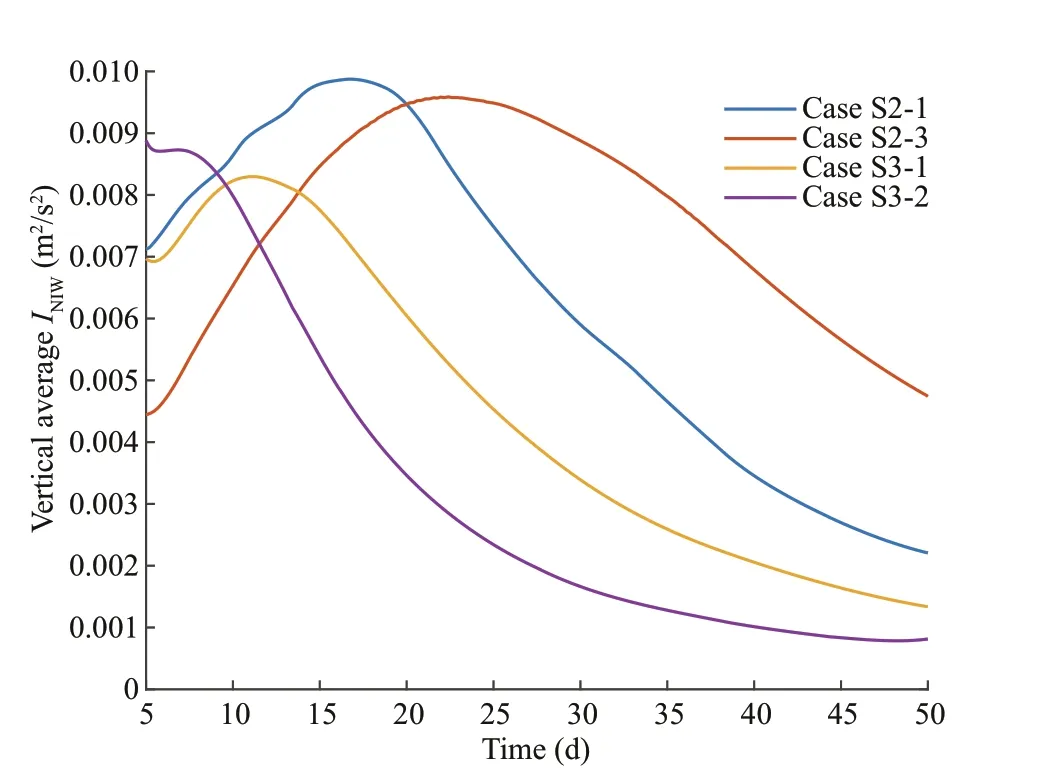
Fig.11 Time series of vertical average NIW intensity for cases S2-1, S2-3, S3-1, and S3-2

From the above analysis, NIW intensity is negatively correlated with eddy radius (horizontal length scale) and local inertial frequency but positively correlated with eddy horizontal velocity. This indicates that NIW intensity can be estimated using the Rossby number (Eq.1). The Rossby number is used to estimate the timescale separation between the mesoscale eddy and internal waves. The small limit of the Rossby number in spontaneous NIW generation indicates that there is little energy transfer between balanced f lows and unbalanced waves. The inf luence of Rossby number on spontaneous IGW generation has been studied in theory and experiment. Vanneste and Yavneh (2004) suggested that the amplitude of IGWs generated spontaneously from transient geostrophic f low is proportional to Ro-1/2exp(-α/Ro),where α is a positive constant. However, Williams et al. (2008) indicated that the IGW amplitude varies linearly with Rossby number by laboratory observations of IGWs radiated from balance f low. In a word, the wave intensity is positively related to Rossby number in the transient generation mechanism.

In the above discussion, we suggest that the Rossby number is not the only parameter aff ecting the NIWs generated spontaneously, and NIW intensity is also determined by the eddy semi-axis and buoyancy frequency. Furthermore, the sensitivity of the eddy horizontal velocity is evidence that Froude number(Fr) is another important parameter, which is positively related to NIW intensity, except the Rossby number.

whereN×LVis the vertical length scale of mesoscale eddy, namely the eddy semiaxis.

In summary, the Rossby number is not only used to divide the dynamic into quasi-geostrophic and ageostrophic regions but is also used to parameterize NIWs generated spontaneously from quasigeostrophic mesoscale eddies. Similarly, the Froude number is important in quantifying NIW intensity,except to be used as an indicator of Kelvin-Helmholtz instability (Capet et al., 2008).

Fig.12 Vertical section of horizontal divergence

Additionally, as Fig.8c & e shows, in the later period of spontaneous NIW generation, theINIWpatterns are parallel to the sea bottom. This is due to the nonlinear interaction between the NIWs generated spontaneously and the waves ref lected from the sea bottom, as shown in Fig.12. In Fig.12, the vertical section of the horizontal divergences of cases S2-1 and S3-1 on the 15th, 23th, and 30thdays are compared.After the forcing move to the bottom of eddy, the NIWs are ref lected by the bottom and form the patterns shown in Fig.12f.

The speed of the forcing in case S3-1 is much faster than in case S2-1, as shown by contrasting Fig.12a, b,c with Fig.12d, e, f. This is also shown by the slopes of theINIWpatterns in Figs.8 & 9. Two moments are selected in the period of NIW generation, and the speed of the forcing can be approximated using the slope of a straight line def ined by the locations ofINIWmaximum at these two moments; i.e., the white dashed lines in Figs.8a, c, d & 9. For cases S2-1, S2-2, and S2-3, spontaneous NIW generation occurs almost over the whole simulation run-time, and theINIWpatterns are clearly curved. Hence, three moments, the 22th,24th, and 26thdays, are selected, and the locations ofINIWmaximum are marked by red points in Fig.8b, d &e. The white dashed broken lines are used to f it theINIWpattern and its slopes represent approximately the speed of the forcing in cases S2-1, S2-2, and S2-3.

Obviously, the slopes in cases S1-1, S1-2, and S1-3(Figs.8a & 9) are the same (about 40 m/s). Hence, the slopes are independent on the vertical semiaxis of eddies. Similarly, the slopes of the broken lines in Fig.8b & d are 40 m/s and 20 m/s. This indicates that eddy horizontal velocity dose not inf luence the speed of the forcing. Comparing cases S2-1 and S2-3, as well as cases S3-1 and S3-2, shows that eddy radius inf luences the NIW generation period, but is independent on theINIWpattern slope. The slope in case S3-1 is about 80 m/s, which is much larger than in case S1-1, as Fig.8a & c shown. This demonstrates thatINIWslopes are negatively correlated with buoyancy frequencyN. The positive correlation of local inertial frequencyfandINIWslope is conf irmed by cases S3-1and S2-1, as shown in Fig.8c & b.Furthermore, despite both the buoyancy and local inertial frequency diff ering between cases S1-1 and S2-1, the same ratioN/fleads to the slopes in these two cases being the nearly the same. Therefore, unlike NIW intensity, which can be regarded as a function of Fr and Ro, the speed of the forcing only depends on the aspect ratioN/f.

4 DISCUSSION

A geostrophic mesoscale eddy radiates IGWs via a transient generation mechanism at the beginning of the simulation. After an initial period of adjustment,the eddy is no longer exactly geostrophic but quasigeostrophic. For a quasi-geostrophic mesoscale eddy,NIWs are generated as a forced linear response to the eddy during its long evolution. Although multiple spontaneous IGW generation mechanisms are investigated in present work, there are still unresolved issues. The location of the boundary between the transient and forcing generation mechanisms and the factors determining the formation of this boundary are still uncertain. In terms of the forcing generation process, we propose that the forcing propagate downward along the eddy axis, but the reason for such propagation is still unknown.

Mesoscale eddy dissipation is correlative on the topographic roughness, as shown by satellite altimetry observation (Gille et al., 2000; Brearley et al., 2013;Zhang et al., 2016). The generation of lee waves by the interaction between seaf loor topography and geostrophic mesoscale eddies can explain this correlation partly (Nikurashin and Ferrari, 2010).Specially, in the Southern Ocean, the energy dissipation for geostrophic f lows is mainly because of the lee wave generation (Nikurashin et al., 2013). We propose that seaf loor topography strengthens NIWs generated spontaneously, and this will be investigated in our future work.

The energy budget of the ocean dictates that diapycnal mixing requires 2 terawatt (TW) to maintain abyssal stratif ication (Munk and Wunsch, 1998), but tidal dissipation in the Open Ocean and windgenerated NIW energy f lux radiated into the ocean interior are estimated to make up only 1-1.42 TW.For this reason, the spontaneous NIW generation mechanism is expected to supply a portion of energy to diapycnal mixing, since continuous energy transfer from mesoscale eddies to internal wave f ields occur in this mechanism. Moreover, the spontaneous NIW generation process is also a pathway for mesoscale eddy dissipation. However, the specif ic energy transfer in this process and its contribution to mesoscale eddy dissipation, as well as the associated diapycnal mixing, need to be further investigated.

5 CONCLUSION

Inertial-gravity waves are generated spontaneously by mesoscale eddies as a forced response. Using a suite of 3D numerical simulations, we obtain the following conclusions.

The internal wave continuum is dominated by NIWs. The baroclinicity of an eddy is the essential for spontaneous NIW generation. In other words, the energy transfer from mesoscale eddies to the NIW f ield is due to the existence of vertical shear of in eddy horizontal velocity. After generation, NIW phases propagate horizontally toward the eddy center and upward in the vertical direction. As with all IGWs, the group velocity is perpendicular to the phase velocity, so that the near-inertial energy propagates downward. Accompanying the upward propagation of NIWs, the patterns of NIWs generated spontaneously move downward along the eddy axis.This is due to NIW forcing generation sources moving downward. The forcing begin to move at the maximum vertical shear of the eddy horizontal velocity, namely the maximum temperature anomaly,located on the sea surface for a sinusoidal mesoscale eddy and on the subsurface for a Gaussian eddy. As the forcing reach the eddy bottom, spontaneous NIW generation is terminated. In the initial NIW generation process, NIWs are conf ined within the eddy and symmetric about the eddy axis. Once the forcing reach the eddy bottom, NIWs are no longer conf ined by the eddy and can propagate freely. Moreover, after free propagation, NIWs are ref lected by the sea f loor,and the nonlinear interaction and wave broken occur ultimately. Hence, mesoscale eddies can aff ect the ocean interior diapycnal mixing via the spontaneous NIW generation mechanism.

Near-inertial wave intensity is determined using background stratif ication, local inertial frequency,and eddy parameters, including eddy semiaxis, radius and horizontal velocity. Among these factors, NIW intensity is the most sensitive to eddy horizontal velocity. Based on the correlation of these factors, in addition to the Rossby number, NIW intensity is also positively correlated with the Froude number. In addition, the inf luence of these factors on the speed of the forcing is also investigated. The mesoscale eddy semiaxis, radius, and horizontal velocity do not inf luence the moving speed. Moving speed only depends on the buoyancy and local inertial frequency and is proportionate to the ratiof/N.

6 DATA AVAILABILITY STATEMENT

The data that support the f indings of this study are available from the corresponding author upon reasonable request.