Mass transport of a mesoscale eddy in the South China Sea identif ied by a simulated passive tracer*

Jun ZHAO , Fan WANG ,4, Shan GAO ,4,**, Yinglin HOU , Kai LIU

1 Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China

2 Key Laboratory of Ocean Circulation and Wave, Chinese Academy of Sciences, Qingdao 266071, China

3 University of Chinese Academy of Sciences, Beijing 100049, China

4 Laboratory for Ocean and Climate Dynamics, Pilot National Laboratory for Marine Science and Technology (Qingdao),Qingdao 266237, China

Abstract To quantitatively investigate the water mass transport of mesoscale eddies, the mass transport induced by a simulated anticyclonic eddy in the South China Sea was evaluated by using the Regional Ocean Modelling System (ROMS) and a built-in passive tracer module. The results indicate that the eddy can trap and transport 51% of the initial water in the eddy core to 689 km from its origin during its lifetime of 100 days, with a stable loss rate of 6‰ per day. During propagation, there is drastic horizontal water exchange between the inside and outside of the eddy. Meanwhile, the vertical mass transport is signif icant, and 65%of the water initially in the mixed layer of the eddy is eventually detrained into the subsurface. A tracer budget analysis of eddy shows that advection is the dominant dynamic process of transport, while the eff ect of mixing is weak, and horizontal process plays a controlling role. Horizontal and vertical advection exhibit opposite patterns and strongly off set each other. Particularly, a distinct dipole pattern is found in the local velocity f ield of the eddy, with signif icant convergence (downwelling) and divergence (upwelling) zones in the anterior and posterior of the eddy, respectively, which is likely related to the driving mechanism of the westward propagation of the eddy. The dipole further induces a vertical overturning cell, through which the surface water in the anterior of the eddy detrains into the subsurface by downwelling and resurface from the posterior of the eddy by upwelling and gradually spreads out of the eddy. The temporal variability in the tracer budget is signif icant, in which horizontal advection is dominant. The propagation acceleration and temporal derivative of the deformation rate are highly correlated with tracer transport, suggesting the potential eff ect of the temporal instability of eddies on the eddy mass transport.

Keyword: mesoscale eddy; mass transport; passive tracer; vertical velocity; mixing

1 INTRODUCTION

The amount of water mass transported by oceanic mesoscale eddies is shown to be very large (e.g., Lee et al., 2007; Early et al., 2011; Zhang et al., 2014).Therefore, mesoscale eddies are believed to play an important role in transporting heat, salt, dissolved carbon, and other biogeochemical tracers in the oceans (e.g., Wunsch, 1999; Chelton et al., 2011; Xu et al., 2019) and further regulating global climate change. Presently, an increasing number of studies have focused on the estimation of eddy-induced mass transport (e.g., Lee et al., 1997; Jayne and Marotzke,2002; Early et al., 2011; Dong et al., 2014). Among others, Zhang et al. (2014) suggested that water tends to be stably trapped in the outermost closed potential vorticity (PV) contour of eddies. Based on this theoretic criterion, the estimated magnitude of water transport by eddies can reach a total meridionally integrated value of 40 Sverdrup (Sv, 1 Sv=106m3/s),comparable to that of large-scale ocean circulation.However, the present criteria and corresponding results are mostly based on the constant quasigeostrophic PV equation in which mixing is neglected.These results are inconsistent with the real state of oceanic eddies, which are both time-variant and have strong mixing. How eddy deformation and mixing aff ect mass transport remains to be further studied.On the other hand, the eff ect of eddy-induced circulation has been widely accepted as a kind of down-gradient mixing and is often embedded in the eddy parameterization scheme in ocean models(Visbeck et al., 1997). However, our understanding of the dynamic mechanism of the parameterization is still incomplete (Marshall et al., 2006; Lee et al.,2007). Moreover, due to the diffi culty of collecting direct measurements of vertical velocity in mesoscale eddies, less attention has been given to vertical velocity in an eddy than to other aspects of eddy dynamics. Most of the studies on the vertical velocity of eddies used an indirect method through the quasigeostrophic Omega equation (e.g., Martin and Richards, 2001; Hu et al., 2011; Nardelli, 2013).However, this method requires observations with high spatial and temporal resolution, which are not easy to obtain when observing mesoscale eddies at present (Martin and Richards, 2001).

Therefore, it is very meaningful to quantitatively evaluate the mass transport of mesoscale eddies and further analyse the corresponding dynamic mechanism to verify the theoretical criteria of eddy-induced mass transport (Zhang et al., 2014) and obtain a better understanding of eddy parameterization schemes.Apparently, the best way to achieve this goal is to directly track and observe the mass transport of a particular mesoscale eddy in the real ocean using tracers (Lee et al., 1997). In early studies, drifters,shipboard prof iles and moored current observations were used to track mesoscale eddies to study the transport capacity of sediments, chlorophyll, and nutrients (Johnson et al., 2005). However, due to the lack of large, f ield-intensive eddy observations, it is still impossible to quantitatively measure the real eddy-induced mass transport from observations(Marshall et al., 2006). As an alternative, taking advantage of the rapid progress in ocean modelling,simulated passive tracers have been increasingly applied to studies on the mass transport associated with mesoscale eddies (e.g., Lee et al., 1997, 2007;Early et al., 2011). Among others, Early et al. (2011)evaluated the water transport properties of an eddy by using a simplif ied passive tracer and f loats in a 2-dimensional reduced-gravity shallow-water model and found that the water that was initially located in the inner core of the eddy (def ined by the zero relative vorticity contour) could be completely trapped by this core and move with the eddy without any exchange with the water outside the core. However, there were two shortcomings in this study. First, it was a 2-dimensional simulation and therefore did not involve the vertical structure of eddies and the corresponding vertical downwelling/upwelling induced by eddies. Second, the mixing process was ignored in the control equation of the passive tracer.At present, simulated passive tracers have been successfully applied to many oceanographic studies(e.g., Fukumori et al., 2004; Qu et al., 2008, 2013;Gao et al., 2011, 2012). However, studies on the mass transport of mesoscale eddies using this method in an eddy-resolving ocean model are still absent.

In view of this, in this paper, we attempt to quantitatively diagnose the mass transport of a typical simulated anticyclonic eddy (AE) in the South China Sea (SCS) using the built-in concentration passive tracer method of the Regional Ocean Modeling System (ROMS), with a special focus on the vertical structure of the mass transport and mixing eff ect on it.Another important issue to address is the relationship between the various characteristics and eddy mass transport.The remainder of this paper is organized as follows.Section 2 provides a detailed description of the ROMS model and the methods that are used in the following analysis. Eddy-induced mass transport is estimated by a passive tracer experiment in Section 3. In Section 4, a tracer budget in a f ixed-volume cylinder moving with the eddy center is examined in detail, and the relationship between the various eddy features and tracer budget terms is analyzed. Section 5 presents the conclusion and discussion.

2 MODEL DESCRIPTION AND METHOD OF ANALYSIS

2.1 Model description

A simulation of mesoscale eddies in the SCS is conducted in this study, which is based on ROMS.ROMS has been widely used in marine ecosystems,sediments, air-sea interactions, etc. (e.g., Warner et al.,2008; Moore et al., 2009; Shou et al., 2018). It is a three-dimensional, free surface, hydrostatic primitiveequation horizontal model with a vertically stretched terrain-following coordinate (Shchepetkin and McWilliams, 2005; Wilkin, 2006; Barth et al., 2008).In our model, nonlinear K-prof ile parameterization(KPP, Large et al., 1994) is adopted for vertical mixing of tracers and momentum.

As one of the largest semi-enclosed marginal seas,the SCS contains a large number of mesoscale eddies at all times, especially in the northeastern SCS and on the western side of the Luzon Strait (Hwang and Chen, 2000; Yuan et al., 2006; Nan et al., 2011). There is evidence that the formation of an AE in this area is related to the Kuroshio intrusion in the northeastern SCS (Zhang et al., 2016). Therefore, we choose the mesoscale eddies in the SCS as the study object. The model domain is then set up to cover the whole SCS and the northwestern Pacif ic Ocean (98°E-147°E,10°S-27°N). Horizontal grid spacing is 1/10°×1/10°.There are 50 sigma levels with terrain-following coordinates in the vertical direction, which are ref ined on the upper layer specif ied by the stretching parametersθs=6.0 andθb=0.1. In the case of deep water, the vertical grid spacing is approximately 10 m within 150 m of the surface, gradually increasing to 480 m towards the bottom of the domain. Bathymetry data are from the ETOPO2 (1/30°) from the National Geophysical Data Center (USA). To reduce the calculation error of the pressure gradient force caused by steep terrain in theσcoordinate system, a Shapiro f ilter is used for terrain smoothing.

The model is initially at rest with climatological temperature and salinity from the Simple Ocean Data Assimilation (SODA) data and then spun up for 60 years forced by the temporal mean seasonal wind stress and heat f lux climatologies based on the National Centers for Environmental Prediction(NCEP)-National Center for Atmospheric Research(NCAR) reanalysis data to reach a state of energy equilibrium and stability. After the spin up, the model conducts real-time simulations from January 2003 to December 2013, forced by wind stress, freshwater f lux and heat f lux from NCEP-NCAR reanalysis data.The boundary conditions are also from the NCEPNCAR reanalysis data, in which the Chapman condition for the free surface, Flather condition for the barotropic velocities, and clamped condition for the three-dimensional f ields (Stevens, 1990).

The long-term mean sea surface temperature (SST)and sea surface salinity (SSS) from the SCS model outputs (Fig.1c & e) are in good agreement with those from WOA13 (Fig.1d & f). The comparison of longterm mean surface velocity between ROMS and that of OGCM for the Earth Simulator (OFES) data also indicates that the simulation by the model is reasonably good (Fig.1a & b).

2.2 Passive tracer method

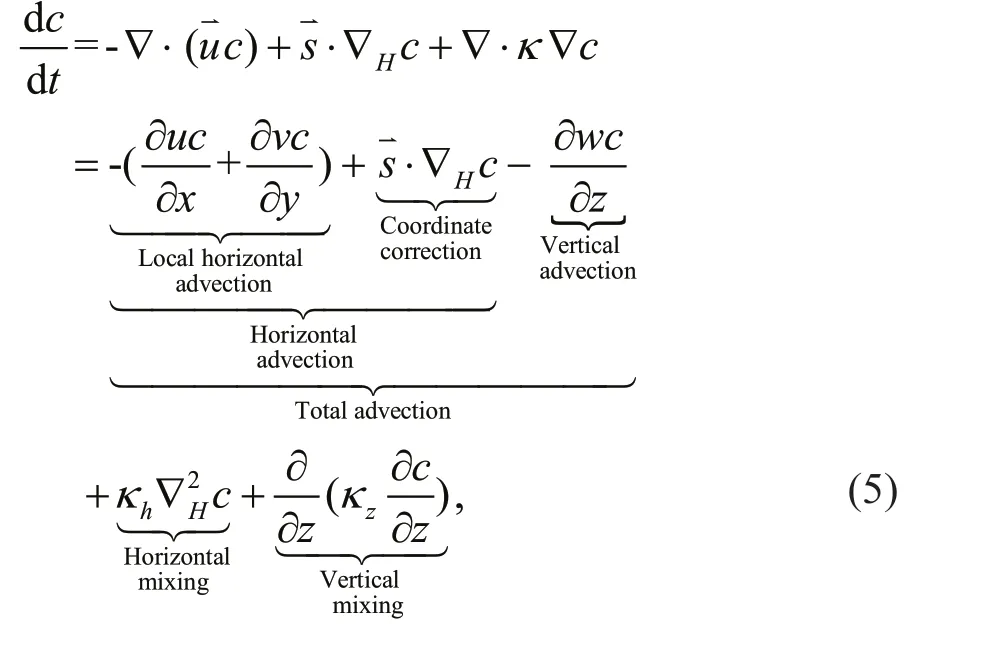
A built-in simulated passive tracer module of the ROMS model (Moore et al., 2004) is used to quantify the water mass transport of an eddy in the SCS. In general, the time evolution of the passive tracer is the same as the advection-diff usion equation of temperature and salinity, except for possible tracer sources and sinks:

According to this equation, if a particular patch of water is uniformly initialized by a passive tracer with no other sources or sinks, the subsequent movement of this tracer indicates the pathway of the initial patch of water. In particular, the relative magnitude of the tracer at a given location to the value of the initial patch describes the concentration of this initial water mass at the location in question.

The passive tracer module of ROMS can provide the data for all terms in Eq.3, which enables us to quantitatively evaluate the temporal evolution of the tracer in the eddy and its corresponding dynamics.

2.3 The method for determining the tracer budget in a moving cylinder

In Section 4, a tracer budget in a cylinder surrounding the eddy core and moving with the eddy center is analysed in detail. The cylinder has a f ixed shape and volume, with its axis set vertically through the real-time surface eddy center (please refer to Section 3 for the detailed conf iguration of the cylinder). The cylinder is regarded as a Lagrangian moving coordinate system, a moving coordinate transformation is used, and the temporal tendency of the tracer concentration relative to the cylinder moving coordinate can be expressed as:

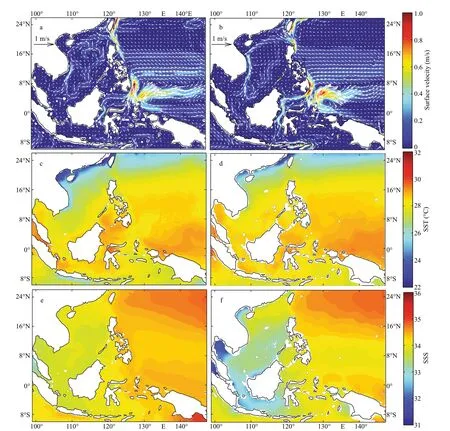
Fig.1 Long-term mean surface velocity (m/s) from ROMS (a) and OFES (b), SST (℃) from ROMS (c) and WOA13 (d), and SSS from ROMS (e) and WOA13 (f)

Using Eq.3, Eq.4 can be rewritten as

In the following analyses, the depth-averaged and volume-average variables are analysed. The square bracket denote the volume average within the cylinder. For example, [c] represent the depthaveraged and volume-average tracer concentrations in the cylinder.

2.4 Eddy detection and tracking method

The eddy detection and tracking method used in this paper is from the method of Dong et al. (2011),which is based on the geometric characteristics of the f low f ield proposed by Nencioli et al. (2010). The eddy identif ication constraint condition defaults that the center of the eddy has the lowest velocity; the velocities on the east and west (north and south) sides of the eddy center have opposite numerical signs, the magnitude increases linearly with the distance from the center point; the rotation direction of the velocity vector must be consistent in the vicinity of the eddy center.

The boundary of the eddy is def ined as the maximum closed stream function around the eddy center. The radius of the eddy is the average distance from each point on the eddy boundary to the eddy center.After determining the selected eddy center, the eddy trajectory is determined by comparing the location of the eddy center in continuous time. In simple terms, this step searches for the next closest polarity eddy within a 15-km search radius of the eddy center that was detected in the previous step. If such an eddy can be found, it will be regarded as a successor of the previous eddy, and the eddy will not become a successor of other eddies; then, it will be followed up. If no qualif ied eddy is found at this time,the search radius will be increased to twice the previous radius the next time. If no eddy is found, the evaluation of the eddy will be terminated.

2.5 Def inition of mixed layer depth and eddy kinematic properties

The mixed layer depth (MLD) in the upper ocean is an important physical parameter to describe the upper ocean. There are many standards for the def inition of the MLD, and the MLD calculated according to diff erent standards may be slightly diff erent. The MLD criterion used in this paper refers to the method of de Boyer Montégut et al. (2004): near the surface temperature threshold at 10-m depth, the threshold is 0.2 ℃.

Considering the balance between the Coriolis force and pressure gradient force, the surface geostrophic velocity anomalies can be derived from the following formula:

The above def initions help to quantify the kinematic properties of eddies and are widely used to describe and study the various properties of eddies (Hwang et al., 2004; Chelton et al., 2011).

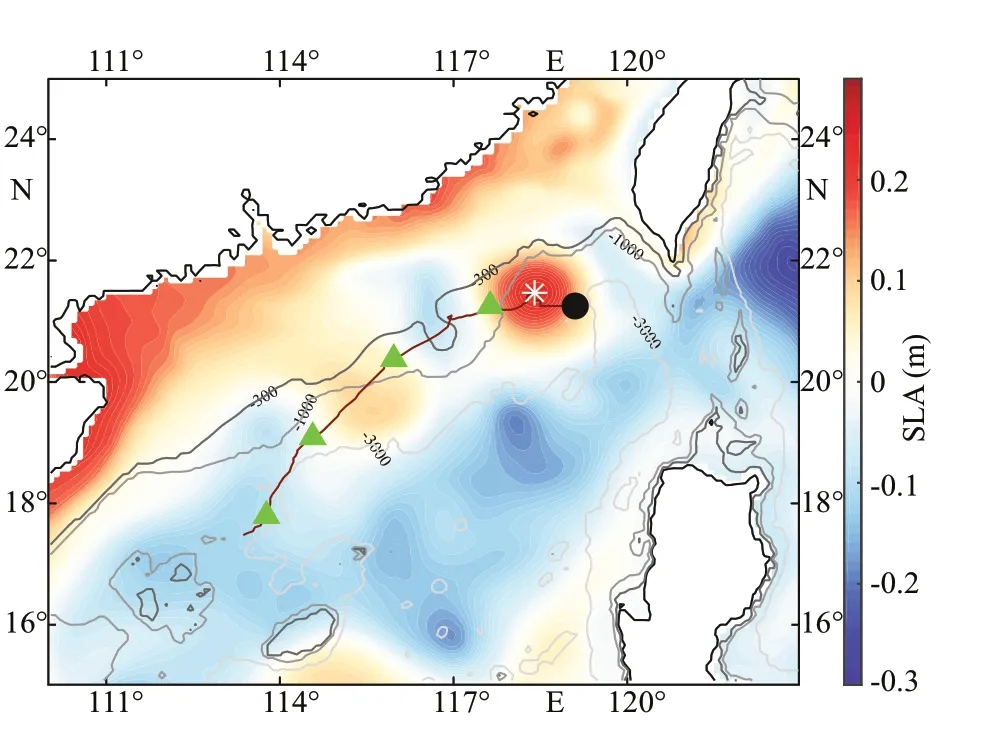
Fig.2 Track of the eddy center during its lifetime (solid brown line) and the SLA (shading) on the day of tracer initialization from the model outputs

3 EDDY-INDUCED MASS TRANSPORT ESTIMATED BY A PASSIVE TRACER

To quantitatively estimate the eddy-induced mass transport, a typical AE (anticyclonic eddy) is chosen as our analysis object from the SCS simulation (cf.Section 2). The track of the eddy shows that this eddy f irst appeared in Southwest Taiwan, China, on November 23, 2012 and disappeared on March 2,2013 (Fig.2). During its lifetime of 100 days, the eddy travelled 689 km (Fig.2), with an average radius reaching 68 km and a mean EKE of 462 cm2/s2, which is very strong. There was a weak steady background southwest f low along its track during its lifetime, with a mean depth-averaged (0-200 m) speed of ＜2 cm/s.The zonal characteristic prof iles of the eddy on the day of tracer initialization showed that the eddy had a symmetric bowl shape structure, with signif icant high temperatures, low salinity and low PV, corresponding to the typical characteristics of a strong warm eddy(Fig.3a-c). The subsurface temperature (salinity) of the eddy center is 3 ℃ (0.2) higher (lower) than that outside the eddy. The MLD (solid black line in Fig.3a& b) of the eddy center is approximately 30 m deeper than that outside the eddy, which coincides with the temperature and salinity (T-S) structure very well,suggesting that there is signif icant convergence and downwelling near the eddy center. The horizontal rotational velocity of the eddy is very strong, with its maximum reaching as high as 0.6 m/s (Fig.3d). As a result, there is a signif icantly low PV region in theeddy core (Fig.3c). The PV contours are not as smooth as those ofT-S, suggesting that there are drastic temporal and spatial variabilities in PV and eddy deformation.and 34.2 in salinity, and between 21 and 27 ℃ in temperature (Fig.4b).

Fig.3 Zonal prof iles of temperature (a), salinity (b), PV (c), and meridional velocity (d) crossing the eddy center (along21.4°N) on the day of tracer initialization

According to the PV distribution in each layer, the passive tracer is then initialized uniformly with a unit value (in arbitrary tracer units per volume, ATU/m3)in the eddy core on December 8, 2012 (Fig.4a).Following Zhang et al. (2014), the core is def ined as the area in the outermost closed contours of PV in each layer. In addition, the day of tracer initialization is set to 15 days after the f irst appearance of the eddy to avoid possible instability at the early stage of the eddy. Most of the tracer-tagged water falls between 21.9 and 23.5 kg/m3in potential density, between 33.8

As the eddy moves westward, the shape and volume of the eddy core continuously changes.Therefore, it is inappropriate for us to analyse the tracer variability in the changing eddy core. As an alternative, all tracer variability analyses in this study are performed in a f ixed shape cylinder surrounding the moving eddy core (the cylinder in Fig.4a). The cylinder axis is set vertically through the real-time surface eddy center, and the cylinder radius and depth are set as 85 km (1.2 times the average eddy radius,larger than 90% of the eddy radii at any time, and 100% that before day 65) and 200 m (97% of the tracers are found above this depth during the lifetime of the eddy), respectively. The eddy core is not completely wrapped in this cylinder at all times because the eddy radius becomes extra-large (～90 km)for 15 days before its termination.

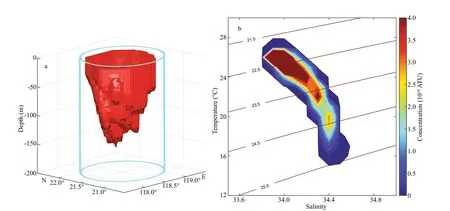
Fig.4 A 3-D demonstration of the initial condition of tracer integration (a); initial distribution of tracer concentration (10 10 ATU)against temperature and salinity (b)

The tracer is then released and traced forward in time under the control of the passive tracer module embedded in the SCS simulation of the ROMS model.The evolution of the tracer is described in detail in the following section.

3.1 The transport of tracer

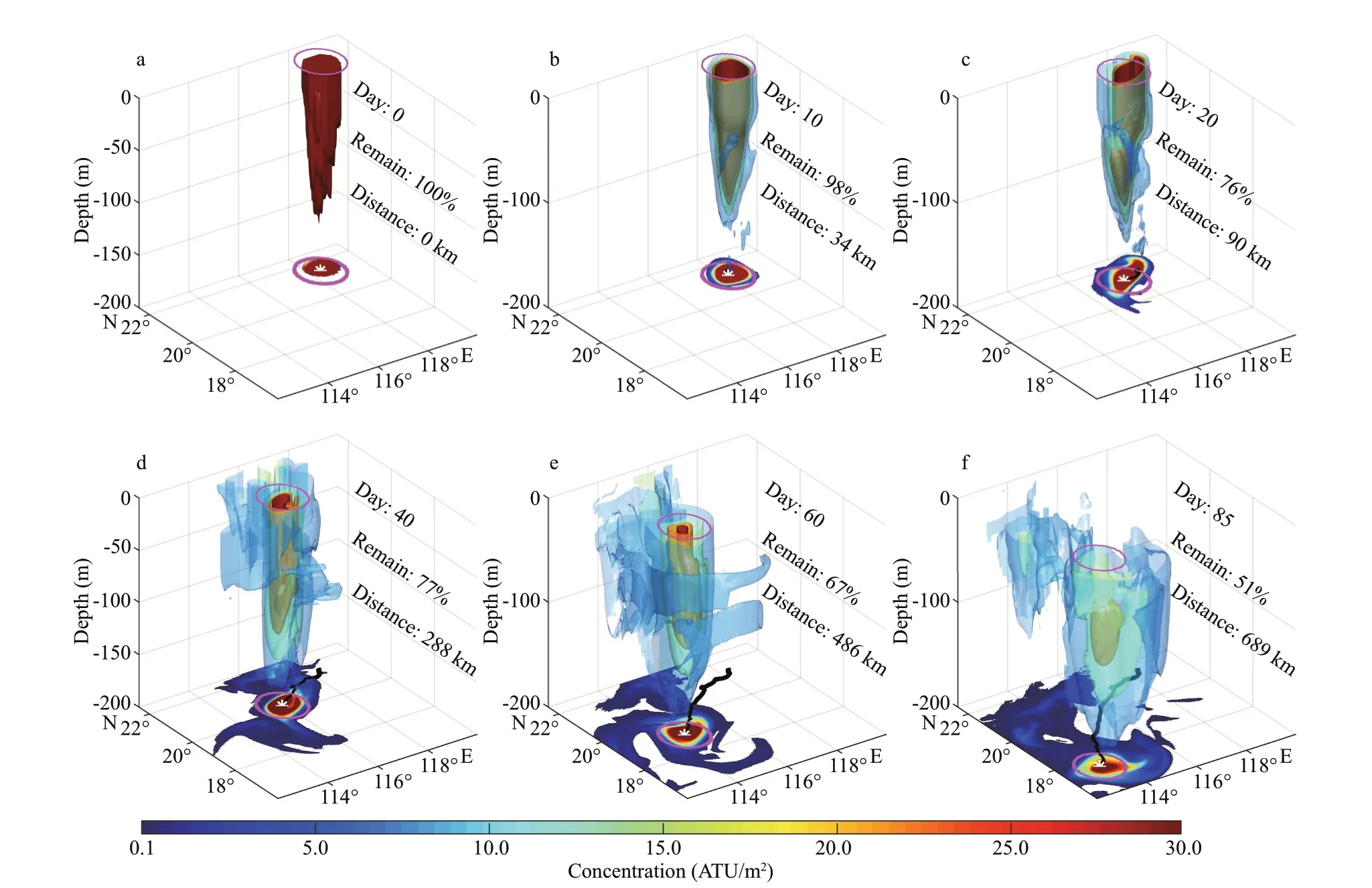
Fig.5 3-D spatial distribution of the tracer concentration on days 0 (a), 10 (b), 20 (c), 40 (d), 60 (e), and 85 (f)

A warm eddy can produce signif icant convergence and dowelling (Hu et al., 2011; Dong et al., 2014; Sun et al., 2018). In this experiment, notable downwelling of tracer-tagged water was observed (Fig.5). The centroid depth of the tracer-tagged water in the cylinder decreased 21 m (from 36 m to 57 m) during the eddy lifetime (Fig.6b). Meanwhile, the MLD also shows a signif icant variation during the lifetime of eddy. The result indicates that the MLD got deepening in the f irst 50 days, ref lecting the strengthening of the eddy during this period, which is conducive to the detraining of the tracer-tagged water. After that, the eddy entered into the decay period, leading to the shallowing of the MLD in the eddy. As a result, there were more detrained water remaining in the subsurface, which is a valid contribution of subduction. On the terminal day, 4.68×1010m3of tracer-tagged water detrained underneath the mixed layer, which accounted for 65% of the total water initially in the mixed layer of the eddy. The downward water f lux induced by this warm eddy reached as high as 5×104m3/s, indicating the important contribution of the eddy to the vertical water exchange, which led to the corresponding eddy-induced subduction (Xu et al., 2016) and diabatic mixing (Bachman and Taylor,2016), and consequently had a noticeable impact on water properties. However, the vertical circulation in the AE (warm eddy) was not found to represent uniform downwelling (Nardelli, 2013; Cotroneo et al., 2016; Pilo et al., 2018). A diploe pattern of convergence and divergence in the eddy core was also found in this experiment. The dynamics will be explored in more detail in a later section to show the structure of the vertical circulation of this eddy.

3.2 Impact on water characteristics

As the eddy moves westward, the horizontal water exchange between the inside and outside of the eddy core signif icantly transforms the characteristics of the water in the eddy. Fifty days later, the temperature of the eddy decreases by as much as 3 ℃, while the salinity is almost unchanged (decreased by only 0.05),which is consistent with the low temperature and low salinity characteristics of the inf low water (Fig.7c &d). The temperature diff erence between water in the eddy and that along the track of the eddy is very large(＞5 ℃), but the diff erence in salinity between them is very small (＜0.2), and the salinity outside the eddy is even slightly fresher than that inside the eddy.Therefore, the variability in density (Fig.7b) is mainly determined by temperature.

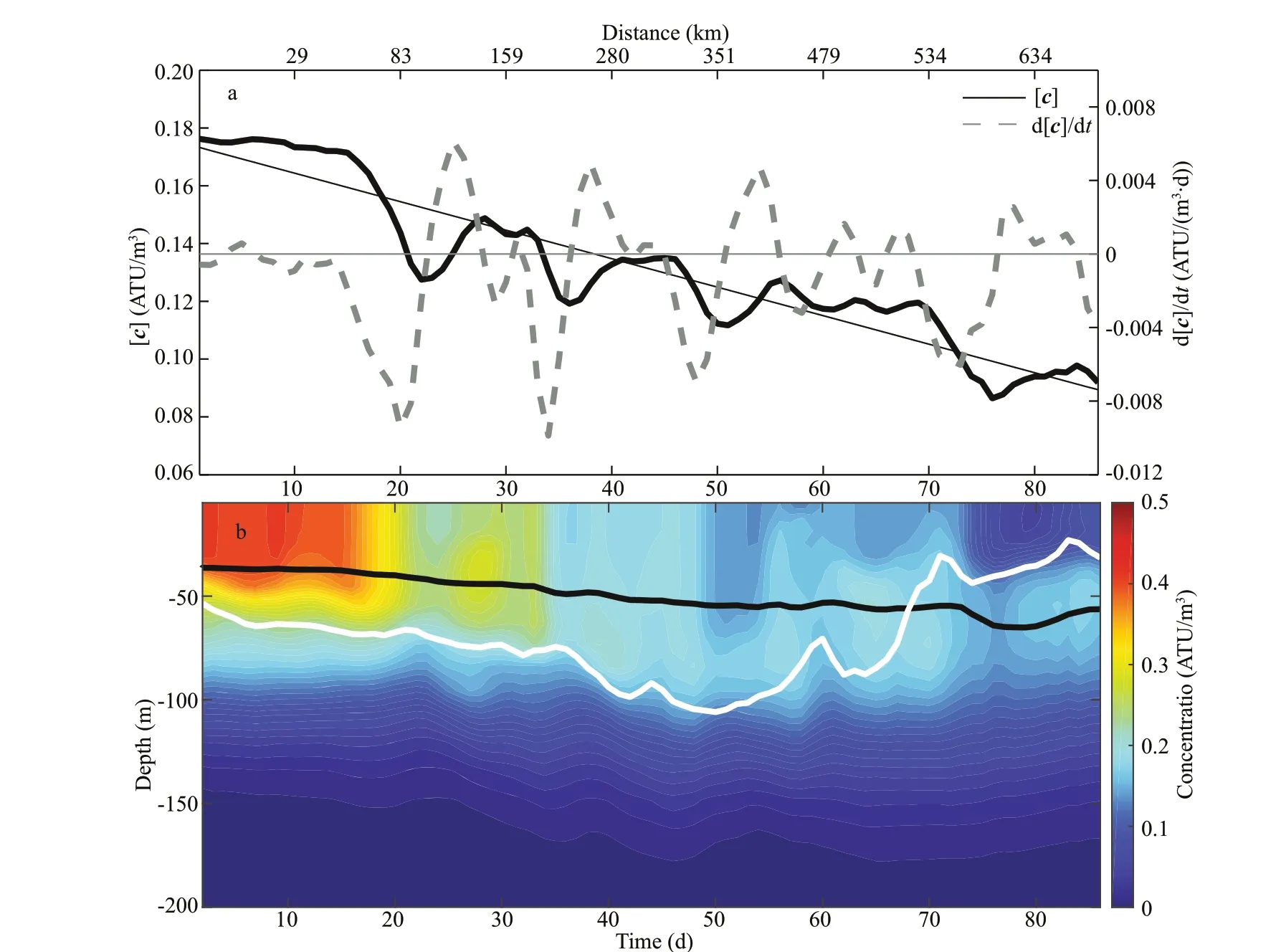
Fig.6 Time series (bold solid black line), trend (thin solid black line), and time derivative (dashed grey line) of the average tracer concentration in the cylinder during the lifetime of the eddy (a); time-depth distribution of the horizontally averaged tracer concentration (shading) and the centroid depth of the tracer-tagged water (solid black line) in the cylinder (b)

Fig.7 Time-depth distribution of anomalies of horizontally averaged tracer concentration (a), density (b), temperature (c),and salinity (d) in the cylinder

Meanwhile, eddy-induced vertical mass transport also signif icantly changes theT-Scharacteristics of subsurface water in the eddy. As shown in Fig.7a,much surface water is subducted into the layer beneath the MLD of the eddy, and the subducted water then makes the subsurface water warmer, fresher, and lighter. Fifty days later, the subsurface temperature increases by 2 ℃ and salinity decreases by 0.2,resulting in a density decrease of 0.5 kg/m3(Fig.7b-d).

Fig.8 Distribution of tracer concentration (10 10 ATU) against temperature and salinity on days 20 (a), 40 (b), 60 (c), and 85(d) over the entire region

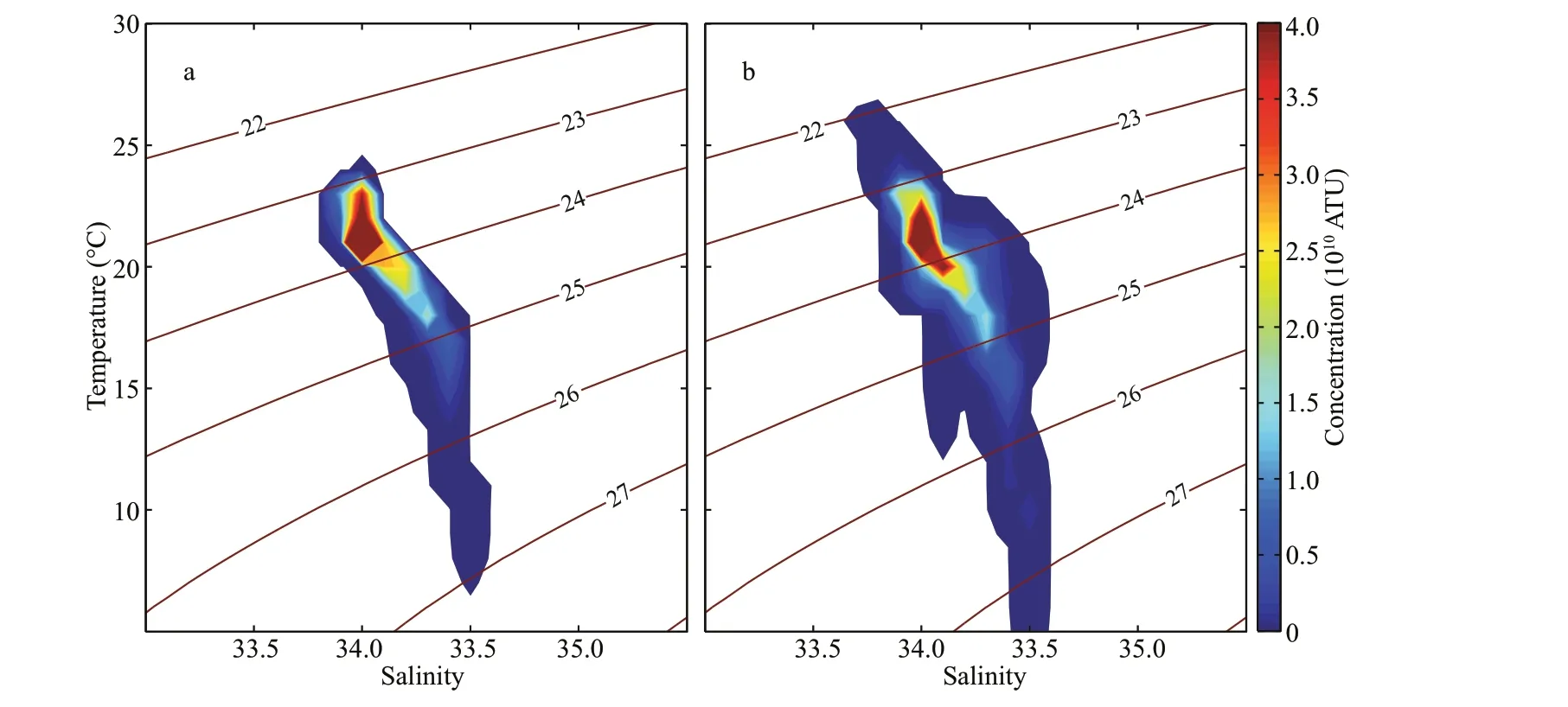
Fig.9 Same as Fig.8 except that the region is inside (a) and outside (b) of the cylinder on the terminal day

The tracer distributions against temperature and salinity (Figs.8 & 9) further illustrate how the tracertagged water is transformed during the lifetime of the eddy. The core of the tracer has an initial density range roughly between 21.5 and 23.5 kg/m3, with temperature between 23 and 26 °C and salinity between 33.8 and 34.2 (Fig.4b). As the tracer-tagged water moves with the eddy, its density increases gradually (Fig.8). By day 40, the characteristics of the tracer are transformed into increased density(＞23 kg/m3) and decreased temperature (＜22 ℃),which is mainly due to the merging of the horizontal inf lux of cold water. At the same time, a small portion of the water is transformed into much denser (25-27 kg/m3) and colder (5-15 ℃) water, suggesting that a part of the surface water sank vertically into the subsurface and mixed with subsurface water to become colder and denser (Fig.8), resulting in the local subsurface water becoming warmer and lighter(Fig.7c & d). Unlike temperature, the variability in salinity is relatively weak both vertically and horizontally during this period (Figs.7d & 8) due to the small salinity diff erence between the water inside and surrounding the eddy. By the terminal day, half of the tracer is still trapped in the cylinder, with its mean temperature decreasing by ～2.5 ℃ and density increasing by 1 kg/m3(Fig.9a), ref lecting the signif icant eff ect of downwelling. Meanwhile, the other half of the tracer is spread outside of the cylinder(Fig.9b). This result indicates that the temperature and density of the water that is still trapped in the cylinder are more concentrated, while that of the water that has leaked outside the cylinder are more dispersed (Fig.9b).

4 TRACER BUDGET IN THE CYLINDER

As described in Section 3, eddy-induced tracer transport occurs in both the horizontal and vertical directions. On the one hand, a large amount of tracer disperses away from the eddy in the horizontal direction; on the other hand, considerable tracer sinks from the surface to the subsurface in the vertical direction. Meanwhile, according to the Eq.3, the two parts of transport are actually controlled by two ocean dynamic processes, advection and mixing. Therefore,it is of great signif icance to quantitatively study the eff ects of the diff erent processes on tracer transport.However, due to the lack of observations, the role of these processes in eddy-induced mass transport has remained obscure.

In this section, by using the daily averaged results of all terms in Eq.3 from ROMS and the tracer budget method described in Section 2.3, a tracer budget in acylinder moving with the eddy center is examined in detail. The temporal mean state, horizontal distribution, vertical structure, and temporal variability of the tracer budget are discussed.

Table 1 Time-volume averaged tracer budget and individual terms over the entire cylinder

4.1 Mean state

Fig.10 Horizontal distribution of temporal mean depth-averaged (0-200 m) tracer budget terms over the cylinder, including Tendency (a), Total Adv (b), Total Mix (c), Horizontal Process (d), Hadv (e), Hmix (f), Vertical Process (g), Vadv (h),Vmix (i), local tendency (j), local total Adv (k), and coordinate correction (l)

4.1.1 Mean value and horizontal distribution 212% and -112% of the tendency term, respectively,i.e., the former is 2 times the latter, indicating that the horizontal process plays a controlling role in the spreading of tracer out of the eddy, while the vertical process off sets 50% of the horizontal process.Moreover, despite their magnitude, their spatial distributions present a counterbalanced pattern(Fig.10d & g). Since the advection terms are much larger than those of the mixing terms, similar counterbalance patterns also appear in the horizontal distributions of Hadv and Vadv (Fig.10e & h), with Hadv being 2.6 times Vadv on average (Table 1).

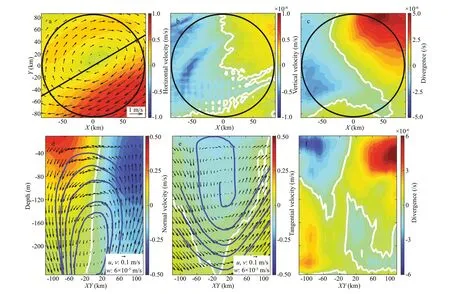
Fig.11 Horizontal distribution (upper row) of the temporal mean depth-averaged horizontal velocity (a), vertical velocity(b), and divergence (c) in the upper 100 m of the cylinder, and vertical section (lower row) of the temporal mean normal velocity (d), tangential velocity (e), and divergence (f) along the diagonal from northeast to southwest and through the eddy center (the solid black line in (a))

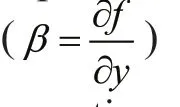
According to the classical theory of the eddy pumping mechanism (Falkowski et al., 1991;McGillicuddy et al., 1998), a signif icant convergence(downwelling) zone symmetrically located around the eddy center is regarded as a symbolic feature of a warm eddy, which is indeed consistent with the observed symmetric distribution of temperature/salinity/MLD in the composite analyses by many previous studies (e.g., Sun et al., 2018). In our study,a symmetric pattern of the tracer tendency also indicates that the water mass transport by eddies is isotropic. However, this result is only valid in the coordinates moving with the eddy. In the Earth coordinates, the divergence f ield of the eddy has a signif icant dipole pattern (Fig.11c), with a strong convergence (divergence) in the anterior (posterior)direction, which is exactly the driving mechanism by which the eddy propagates westward. Note that the Total Adv (Fig.10b) is one order of magnitude smaller than the local total Adv (Fig.10k) due to the off set by the coordinate correction (Fig.10l), which indicates that the dipole of convergence and divergence of the eddy in Earth coordinates is much stronger than the weak spreading pattern in the eddy moving coordinates. The dipole of convergence and divergence is bound to produce a corresponding strong downwelling zone and upwelling zone, which will certainly ref lect the vertical structure of the eddy.

4.1.2 Vertical structure

Considering that the horizontal distribution of most tracer budget terms is nearly symmetrical with respect to the eddy propagation direction (31° west by south),the temporal mean tracer budget terms on the vertical section along the propagation direction and through the eddy center (the black solid line in Fig.11a) are examined as follows, with particular attention to the vertical structure of the dipole of convergence and divergence (Fig.12).

The tendency term (Fig.12a) shows an axisymmetric spreading pattern consistent with its horizontal distribution (Fig.10a).cin the eddy core decreases signif icantly, while it increases around the core and below the mixing layer, indicating that a large proportion of water subducts to the subsurface. The Total Adv and Total Mix in this section appear to have the same order of magnitude and partially counterbalance each other. Overall, however, the eff ect of Total Adv (65%) is still dominant and is 1.8 times larger than that of Total Mix (35%). As the main component of Total Mix, Vmix has an obvious feature: it is mainly conf ined in the mixed layer, and the eff ect under the mixed layer decreases sharply,illustrating the strong Vmix in the mixed layer.Meanwhile, the eff ect of Hmix is very weak, but it is not conf ined in the mixed layer and can reach a deeper depth of 150 m.

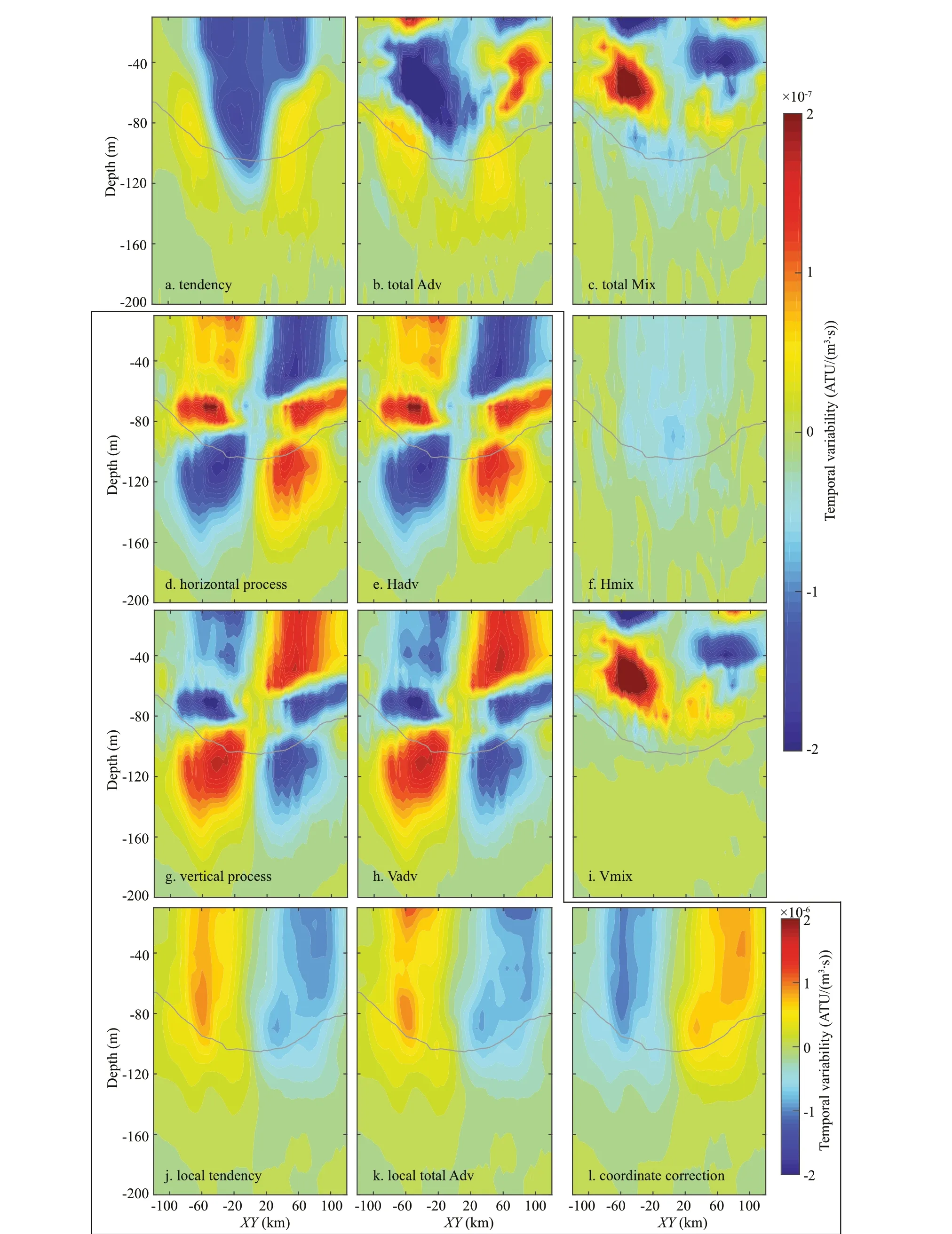
Fig.12 Same as Fig.10, except for the temporal mean tracer budget terms on the vertical section along the diagonal from northeast to southwest and through the eddy center (the solid black line in Fig.11a)

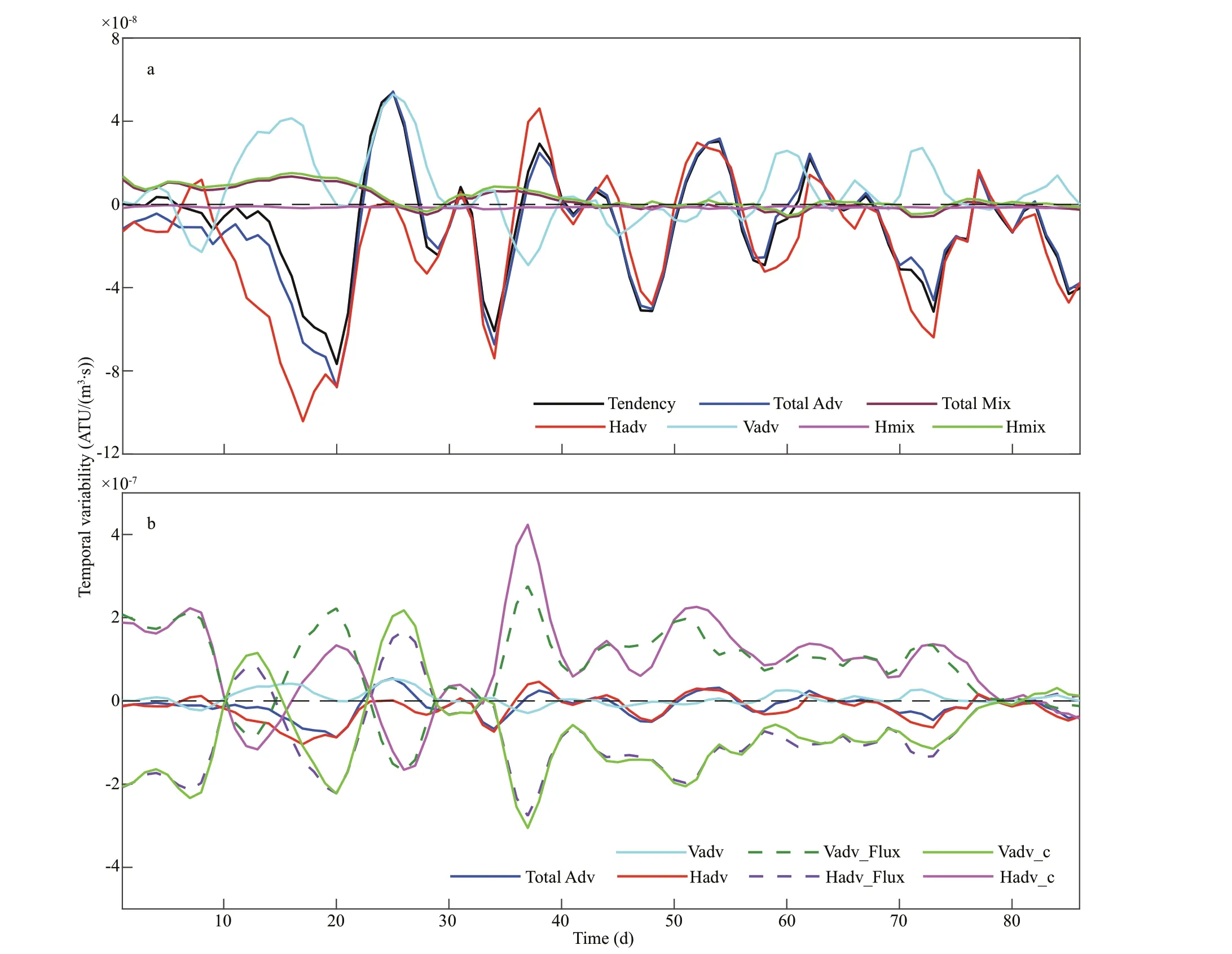
Fig.14 Temporal variation in the volume-averaged tracer budget (a) and the components of advection terms (b) in the cylinder during the experiment

Analogous to the horizontal distributions, the vertical distribution patterns of Total Adv and local total Adv (Fig.12b & k) are also quite diff erent. Since the Total Adv is a result of the eddy motion coordinates,it looks relatively weak, which indicates that the Total Adv has no strong impact on the leakage of the water mass from the eddy. However, from the viewpoint of the Earth coordinates, the local total Adv shows a signif icant dipole pattern of convergence and divergence in its vertical structure, which has been described in its horizontal distribution. On the left(right) side of the prof ile, the strong convergence and downwelling (divergence and upwelling) leads to a signif icant increase (decrease) incpenetrating the mixed layer to the subsurface, with its major inf luence depth reaching as deep as 100 m, which is in good agreement with the velocity f ield (Fig.11). The quivers and streamlines in Fig.11d show the tangential and vertical velocities on the prof ile in Earth coordinates.This indicates that in addition to the strong upwelling and downwelling, there is a net lateral f low in the eddy core, by which the subsurface upwelling water on the right side is transported to the convergence zone through the upper layer. As a consequence, the eddy core, which features the highccenter, will be driven to shift towards the left. However, if we observe the velocity f ield in the cylinder moving coordinates (Fig.11e), this surface lateral current disappears due to the coordinate correction and is replaced by an overturning cell. Through this overturning cell, the highcwater f irst detrains from the surface layer of the left side of the eddy core to the subsurface by downwelling, then part of it merges into the upwelling zone of the right side and resurfaces and gradually spreads out by local divergence. A similar vertical structure can also be found in a group of anticyclonic eddies in the East Australian Current region simulated by Pilo et al. (2018). Of course, this velocity f ield on the prof ile represents only net transport; due to the fast swirl of the eddy, the real trajectory of the water mass is supposed to be spiral.

This result, however, is contrary to our knowledge that the AE core is uniformly downwelling (e.g.,Paterson et al., 2007; Nemcek et al., 2008; Oliver and Holbrook, 2014). In particular, there seems to be a signif icant upwelling zone in the posterior of the eddy, which is likely correlated with eddy propagation.

4.2 Temporal variability

Figure 14 shows the temporal variations in the tracer budget and its components averaged in the cylinder during the tracer experiment. This indicates(Fig.14a) that the temporal variability of the tracer tendency is very signif icant, with its STD (3.3× 10-8ATU/(m3·s)) 3.3 times its average (-1.0× 10-8ATU/(m3·s)),in which Hadv plays the most dominant role. The correlation coeffi cient (R) between Hadv and the tendency is 0.80, while all the other terms do not have a signif icant correlation with the tendency. As the second major factor, Vadv partially off sets the eff ect of Hadv. As a result, the correlation of the Total Adv with the tendency reaches as high as 0.99. The variability of the mixing terms is relatively mild, and the STD of Total Mix is only 1/5 of the Total Adv. The variability of Hmix is very weak, while the variability of Vmix is relatively large, barely comparable to that of Vadv.Further inspection of the individual components of the advection terms indicates that Hadv_c and Vadv_c are quite similar but with opposite signs, with their negative correlation reaching as high as 0.90(Fig.14b). The large degree cancellation between these two terms results in a reduced total advection that is one order of magnitude smaller. At the same time, due to the large cancellation between Hadv_f lux(Vadv_f lux) and Hadv_c (Vadv_c), Hadv (Vadv) is also reduced signif icantly. Please refer to Section

4.1.2 for the interpretation of the cancellations.

4.3 Correlation between eddy kinetic features and tracer budget terms

Previous studies (Chelton et al., 2011; Zhang et al.,2014) suggest that some eddy kinetic features are likely highly correlated with the eddy mass transport capability. Among others, the nonlinearity of eddies(N) is considered to be an important index of mass transport by eddies. As Chelton et al. (2011) pointed out that as long asN＞1, there will be a parcel of trapped water mass within the eddy core that is transported with eddy propagation. Since the meanNof this eddy is 4.8 with its maximum reaching 8.5, the eddy in this study is supposed to have an excellent water mass trapping capability. Another feature that is considered to be possibly correlated with the mass transport of eddies is the deformation rate of eddies.According to its def inition (Section 2.5), the physical meaning ofγis the degree in which the eddy shape deviates from the circular shape. Therefore, it is reasonable to assume that the largerγis, the more irregular the eddy shape is, and the faster the tracer leaks. Moreover, the other features associated with the eddy intensity, such as EKE,U, radius, etc., are also possibly relevant to eddy mass transport.

Since the mass transport capability of the eddy can be quantif ied by the tendency term of the above tracer budget, i.e., the variability of the averaged tracer concentration in the cylinder, the correlations between the features and tracer budget terms of the eddy are then evaluated in detail as follows.

The period for all analyses in this section is set from the 15thday to the 65thday of the tracer experiment for 2 reasons. First, the volume of the initial tracer-tagged water is only 1/5 that of the cylinder, and there is a considerable blank area between the initial tracer region and the cylinder boundary (Fig.4a). Therefore, it takes approximately 15 days for the initialized tracer to reach the boundary and start leaking from the cylinder, which results in the tendency term being nearly zero for the f irst 15 days (Figs.6a & 14a). Second, the lifetime of a typical eddy is usually divided into three stages:youth, mature, and aged (Liu et al., 2012; Lin et al.,2015; Zhang et al., 2016). The f irst and last 20% of the lifetime is the “youth” stage and the “aged” stage,respectively. There are drastic variations in the state of the eddy during these two stages. Meanwhile, at the “mature” stage (the middle 60% of the lifetime),the status of the eddy is relatively stable (Lin et al.,2015). To avoid the impact of the diff erent stages, the“mature” stage is chosen as the analysis period.Considering that the tracer experiment started on the 15thday when the eddy f irst appeared, the “mature”period was set from the 5thday to the 65thday of the experiment. As a result, the intersection of these two time periods was from the 15thday to the 65thday of the experiment (referred to as the “mature period”hereafter). In addition, the tendency is found to be low-frequency variability. Therefore, an 8-day low pass f ilter is applied to all the variables in the analyses to avoid the impact of the high frequency variations in the features. The power spectrum density analysis of the tendency term indicates that the remaining lowfrequency signal after f iltering accounts for 85% of the total power.

Unexpectedly, the result indicates thatNdoes not have a good correlation with the tendency. It seems thatNdoes not directly impact the mass transport capability of the eddy. Meanwhile, neitherUnorsshow good correlations with the tendency. As Chelton et al. (2011) pointed out,Nhas a threshold; therefore,as long as it passes the threshold, i.e.,N＞1, the eddy could have a good mass transport capability.

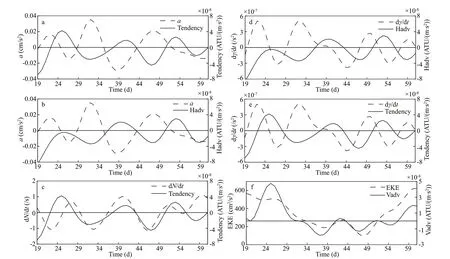
Fig.15Variabilityoftendencywith a (a),Hadv witha (b),tendency with (c), Hadv with (d), tendency with (e),andVadv withEKE (f)during the“matureperiod”

Similar analyses of many other features, such as the eddy radius, EKE, and PV, are also conducted;however, no high correlation with the tendency is found. Of course, it cannot be certain that eddy mass transport has nothing to do with these features because it is probably the result of the interaction of these features with diff erent dynamics, which needs careful study in the future. For example, the EKE is highly positively correlated with the Vadv (R=0.74, Fig.15f),while it is also negatively correlated with the Hadv(R=-0.53), and their interaction results in a poor correlation between EKE and the tendency.

However, the correlation of some temporal derivatives of eddy features (Nandγ) with tendency is very signif icant, which suggests that the temporal instability of the eddy probably plays an important role in eddy mass transport. An eddy in drastic adjustment tends to leak extensive water mass from the eddy.

5 SUMMARY AND DISCUSSION

To quantitatively investigate the water mass transport of oceanic mesoscale eddies, the mass transport induced by an AE in the SCS was evaluated by using a built-in simulated passive tracer of the ROMS model.

The results of the tracer experiment indicate that the eddy was robust and stable. It trapped and transported 51% of the initial tracer-tagged water in the eddy core to 689 km from its origin during its lifetime of 100 days, with a stable loss rate of approximately 6‰ per day. This result conf irms the strong long-distance mass transport capability of mesoscale eddies, which has been proven by many studies (e.g., Early et al., 2011; Dong et al., 2014;Zhang et al., 2014). However, it also indicates that more than half of the water that was initially trapped by eddies leaked out of the eddy during eddy propagation, which suggests that it is necessary to quantitatively evaluate the loss quantitation when we analyse the contribution of eddy-induced mass transport to large-scale circulation.

During the propagation of the eddy, there was a dramatic horizontal water exchange between the inside and outside of the eddy core. Some tracertagged water that has f lowed out of the cylinder may f low back into the eddy core. This result is consistent with the observations reported by Qiu et al. (2019).Meanwhile, the eddy-induced vertical mass transport was also very signif icant, and approximately 60% of the water initially in the mixed layer of the eddy was eventually detrained into the subsurface. As a result,the water in the mixed layer of the eddy became colder and denser, and the water in the subsurface became warmer and lighter.

To evaluate the eff ects of diff erent dynamics on transport quantitatively, a tracer budget in a f ixedvolume cylinder moving with the eddy center is examined in detail. The result indicates that advection is dominant, accounting for 120% of the tendency,while the eff ect of mixing is weak, explaining -20%.It is unexpected that the overall eff ect of the Total Mix on the tracer tendency is positive, which is mainly due to the contribution of Vmix. This suggests that mixing may help to conserve the water mass in eddies. This result is contrary to our common sense that mixing generally reduces the tracer concentration. The mechanism driving this result needs further study.The eff ect of the horizontal process is 2 times that of the vertical process, indicating that the horizontal process plays a controlling role in the mass transport of the eddy. Horizontal and vertical advection are found in opposite patterns and strongly off set each other.

The horizontal distribution and vertical structure of the local velocity f ield of the eddy all show distinct dipole patterns, which have signif icant convergence(downwelling) and divergence (upwelling) zones in the anterior and posterior of the eddy core, respectively.Due to the dipole, there is an overturning cell in the vertical direction, through which the surface water in the anterior of the eddy tends to detrain into the subsurface by downwelling and partially resurface from the posterior of the eddy by upwelling and gradually spreads out.

Because the vertical velocity in the mesoscale eddy is not easy to measure directly, less attention has been given to the vertical velocity in the eddy than to other aspects of eddy dynamics. An indirect method using the quasi-geostrophic Omega equation is applied in most studies of the vertical velocity of eddies (e.g.,Martin and Richards, 2001; Hu et al., 2011; Nardelli,2013), which, however, requires observations with high spatial and temporal resolution. In classic theories of the vertical velocity of an eddy, such as the eddy pumping mechanism (McGillicuddy et al.,1998), the vertical velocity in the eddy core and the corresponding downwelling (upwelling) zone should be centrosymmetric around the eddy center at all depths, which seems consistent with the observed symmetric distribution of temperature/salinity/MLD in the composite analyses by many previous studies(e.g., Zhang et al., 2014; Sun et al., 2018). By using satellite altimetry and Argo prof iles, Sun et al. (2018)and others investigated eddies in the SCS. Their results indicated that the composite horizontal velocity f ield presents a fully symmetric structure around the normalized eddy-coordinate center at all depths. In our study, however, the vertical velocity within the eddy core presents a signif icant dipole pattern. Similar dipole patterns of vertical velocity were found in a recent model study of anticyclonic eddies in the East Australian Current region by Pilo et al. (2018). However, the dipole pattern was considered a result of eddy distortion in their study. A good observational evidence is also found in a study of Chelton et al. (2011), in which the Inf luence of mesoscale eddies on near-surface oceanic chlorophyll is analyzed using the satellite estimates. It can be seen in this study, there is a signif icant dipole pattern of the near-surface chlorophyll anomaly, with a negative(positive) anomaly in the anterior (posterior) of the eddy core, which obviously corresponds to the downwelling (upwelling). However, the dipole pattern of the chlorophyll anomaly is taken as a result of the interaction between the horizontal advection of eddies rotation and the meridional gradient of the chlorophyll distribution. In our opinion, if we consider the propagation of the eddy, it seems necessary to have such a constant dipole structure to drive the eddy to move westward and the occurrence of eddy distortion is not necessary. Therefore, it might be related to the driving mechanism for the westward propagation of the nondispersive baroclinic Rossby wave. As the dipole pattern is correlated with eddy propagation, eddies with diff erent propagation speeds are likely to have diff erent patterns, which requires a theoretical analysis in more detail. Moreover, since these results are only a model result of a single warm eddy, it is still uncertain whether these results can represent the situation of an eddy in the real ocean.Furthermore, the situation of a cold eddy seems quite diff erent from that of a warm eddy (Nardelli, 2013).Therefore, it is necessary for us to perform further composite analyses on the vertical velocity of more diff erent types of eddies.

The temporal variability in the tracer budget is found to be very signif icant, in which horizontal advection is dominant. The propagation acceleration and the temporal derivative of the deformation rate are highly correlated with the tendency term,suggesting the potential eff ect of the temporal instability of eddies on eddy mass transport. To date,most of the theoretical solutions related to mesoscale eddies (e.g., Jayne and Marotzke, 2002; Dong et al.,2014; Zhang et al., 2014; Yang et al., 2015) are constant or time-independent. This result reminds us that it is necessary to construct a time-dependent theoretical model of mesoscale eddies in which the temporal derivative terms are considered.

6 DATA AVAILABILITY STATEMENT

The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.

7 ACKNOWLEDGMENT

Supercomputing resources were provided by High Performance Computing Center of Institute of Oceanology of Chinese Academy of Science. We also thank Dr. Ronghua ZHANG (Institute of Oceanology,Chinese Academy of Sciences) and Tangdong QU(University of California, Los Angeles) for their helpful advices. The authors would like also to thank reviewers for their comments and the developers of ROMS for open access to their code.