送风参数对岩心冷柜内温度场影响的CFD研究
刘泽勤 于永杰 李 杰
(天津商业大学 天津市制冷技术重点实验室 天津 300134)
岩心作为一种重要的实物地质材料[1-2],开采成本昂贵,若不能妥善储藏会导致其结构和物理特性发生质变,将对岩心资源造成极大的浪费,储藏的温度、湿度等环境参数直接影响岩心的品质,对于一些特殊岩心更需要恒温恒湿的储藏条件来模拟岩心本身所存在的环境,保证岩心中各成分不发生明显变化[3]。目前岩心库多采用大型冷库进行储藏,但大型冷库占地面积大,建设成本和初投资较高,对于岩心总量少的企业机构,使用大型冷库库存率低,制冷系统却要为整个冷库提供冷量,能源消耗高,代价较大[4]。自动化立体岩心冷藏柜为岩心总量少的中小型企业机构探索了新思路新方案,其由多组独立控制的小空间冷柜组合而成,自动化程度高,克服了初投资和运行成本高的问题,但由于纵向较高,更容易出现温度分布不均匀现象,若不能对其内部气流组织进行优化,很难满足用户单位对整个冷柜温度精度控制的要求。岩心冷柜内的温度分布很大程度取决于送风参数(送风温度、送风速度),送风参数的差异直接影响冷柜内部温度场分布,也直接影响到岩心储藏品质,因此采用合理的送风参数控制温度波动范围至关重要。
计算流体力学(computational fluid dynamics, CFD)用于求解各种流体的流动和换热问题[5-7]。国内外学者基于CFD技术对冷库内部气流组织的影响因素进行了研究,为CFD技术在实际工程中的应用提供有力理论支持。胡耀华等[8]通过数值模拟对一间装配式猕猴桃冷库进行研究分析,证明CFD数值模拟在冷库内流场设计切实可行。芮文琴[9]利用数值模拟方法采用不同送风方式对小型装配式冷库进行研究,得出影响冷库内部气流组织的主要因素为送风方式、送风速度等,为冷库优化设计提供参考。Z. Ghiloufi等[10]对某大型椰枣冷藏室建立三维CFD模型,确定了合适的预冷条件,大幅缩短了预冷时间,冷藏室内温度分布更加均匀。尹义金等[11]通过数值模拟研究了风速对冷库内部温度场的影响,在一定范围内,送风速度的增加促进了对流换热,冷库降温能力增强。刘清江等[12]利用Fluent软件对高大空间气流组织分布规律进行模拟研究,实测结果和模拟结果吻合较好,对高大空间温度场及速度场的模拟提供了理论支持。O. Rouaud等[13]对食品加工洁净室分别建立了标准k-ε模型和RNGk-ε模型,通过与实验结果对比分析,发现RNGk-ε模型更适合洁净室的气流计算。张悦[14]利用实验研究和数值模拟相结合的方法,研究了送风速度对船舶冷库内温度场和速度场的影响,得出在一定条件下适当增加风速能有效促进气流组织进一步均匀。白通通[15]通过数值模拟研究了某苹果冷库内部流场,得出竖壁贴附送风更有利于热量交换,大幅提升了冷库内气流的均匀性。
本文结合某地质研究所自动化立体岩心冷柜建设项目实际情况,以雷诺准则、弗劳德准则、欧拉准则等为依据[16],建立工程原型与实验模型间主要的流体流动和换热特征对应关系,并搭建相应模型实验台,运用实验研究和数值模拟相结合的方法,研究送风温度和送风速度对岩心冷柜温度场分布的影响,得到最优送风参数,保证冷柜内部温度均匀合理,控制温度波动范围和岩心储藏品质,为立体冷柜的工程实践提供理论支撑。
1 数值计算模型
1.1 物理模型
本课题数值模拟的模型依据相似性原理将某地质所一组岩心冷柜按相似比2∶1进行缩小,原型冷柜空间尺寸为4 000 mm(长)×1 000 mm(宽)×8 300 mm(高),故按相似比缩小后的模型尺寸为2 000 mm(长)×500 mm(宽)×4 150 mm(高),冷柜壁厚60 mm,模型实验台如图1所示。在冷柜顶部右侧设置尺寸为50 mm(长)×500 mm(宽)的送风口,在冷柜顶部左侧设置尺寸为50 mm(长)×500 mm(宽)的回风口;模型中岩心均匀放置在岩心托盘上,满载岩心托盘简化为800 mm(长)×400 mm(宽)×400 mm(高)的长方体,相邻两岩心托盘之间留有200 mm宽空气流道,左右两列托盘距冷柜侧壁面100 mm,前后壁面各50 mm。冷柜满负载工况如图2所示,考虑到岩心区域数学模型的复杂性,每一个岩心托盘满载时简化为各向异性多孔介质模型[17],单个岩心简化为直径60 mm、长800 mm的圆柱实体,物理模型如图3所示。

图1 岩心冷柜模型实验台
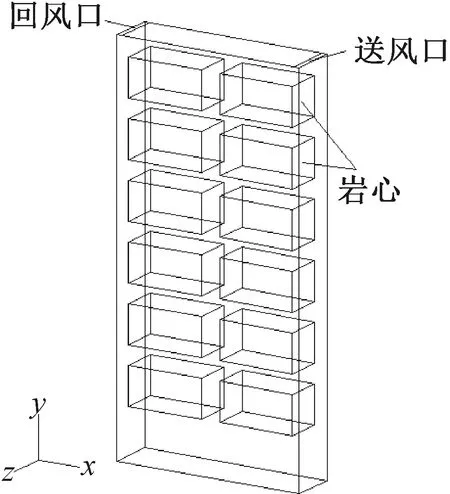
图2 岩心冷柜模型
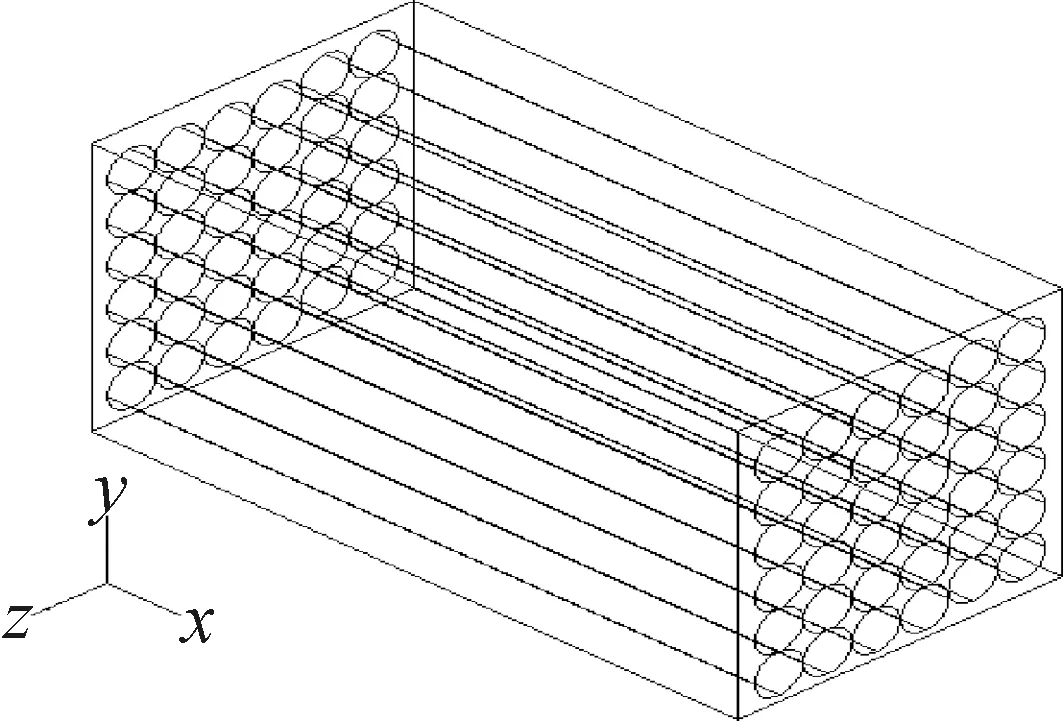
图3 满载岩心简化模型
1.2 数学模型
为建立一个合适的数学模型来描述冷柜内部流动换热的规律,需对模型进行适当简化,在岩心冷柜的数值模拟计算中,进行如下假设:
1)冷柜内部空气为不可压缩流体且符合bous-sinesq假设[18];
2)空气不可压缩,不参与反射、辐射;
3)忽略冷柜内货架等支撑物对流场的影响;
4)岩心为密度均匀的圆柱体;
5)冷柜密封良好,与外界只有热量传递,不存在质交换。
基于上述假设,为使模拟结果更接近实际情况,在冷柜内部流场计算中选用对竖壁贴附射流具有较好预测性能的RNGk-ε模型,描述该模型的控制方程如下:
连续性方程:
(1)
能量方程:
(2)
动量方程:
(3)
k方程:
(4)
ε方程:
(5)
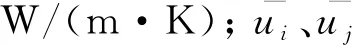
su为多孔介质的附加阻力,该动量源项由黏性阻力和惯性阻力构成,表达式如下[19]:
(6)
阻力系数可通过半经验公式Ergun方程求解计算,表达式分别为:
(7)
(8)
式中:vi为岩心区域的空气流速,m/s;α为多孔介质的黏性阻力系数,1/m2;c2为惯性阻力系数,1/m;Dp为多孔介质的特征长度,m;e为货物区的孔隙率。
高度各项异性多孔介质模型可能存在收敛问题,可将其他方向的系数设置为主流方向的3个数量级以内,本文设置y、z方向阻力系数为x方向的1 000倍,各个方向阻力系数值如表1所示。

表1 阻力系数
2 边界条件及网格无关性验证
模拟前处理使用ICEM软件进行建模和网格划分,对送、回风口及岩心周围网格进行局部加密,并在Fluent软件中设定边界条件和求解方法,使用Tecplot和Origin软件对模拟结果进行后处理。根据地质所提供的岩心储藏情况,多组冷柜并列安置在内有保温效果的无窗专用大洋岩心库内,制冷系统设置在冷库外部,库内温度波动受外界影响较小,数值模拟时冷柜外界温度取库内恒定温度18 ℃;冷柜内计算域分为空气流体区域和岩心多孔介质区域,岩心表面设置为耦合壁面(wall),初始平均温度为12.1 ℃;送风口位于冷柜顶部右侧,采用竖壁贴附射流组织形式将冷风送入冷柜内部,送风方向垂直于顶板竖直向下,送风边界条件设置为速度入口(velocity-inlet),送风速度由风机盘管(标准风盘FP-85,最大风量850 m3/h)的实际调风能力设置三档风速,分别为3.5、4.2、4.7 m/s,考虑到地质所提供岩心储藏控制温度为2.5 ℃±1.5 ℃,送风温度设为-3、-2、-1、0、1、2 ℃;回风口位于冷柜顶部左侧,设置为自然出流边界条件(outflow);冷柜壁面设置为无滑移壁面边界条件(wall),顶部壁面设置为绝热边界条件。
在进行数值模拟计算之前,为使模拟结果具有较高的可靠性,需对网格无关性进行验证,图4所示为典型截面z=0.25 m温度监测点布置(同后文实验测点设置)。图5所示分别为送风温度-3 ℃,送风速度4.2 m/s,网格数分别为75万、177万、257万、342万,垂直监测线H1、H4和H7的温度分布情况,可知,当网格较为稀疏,网格数较少时,温度值差异较大,模拟结果稳定性和准确性较差,当网格数为257万和342万时,三条监测线的温度值基本相同,可以认为网格数为257万时已经达到了网格独立解,为节省计算机资源和计算时间,选取网格数为257万的网格进行后续的数值模拟计算。
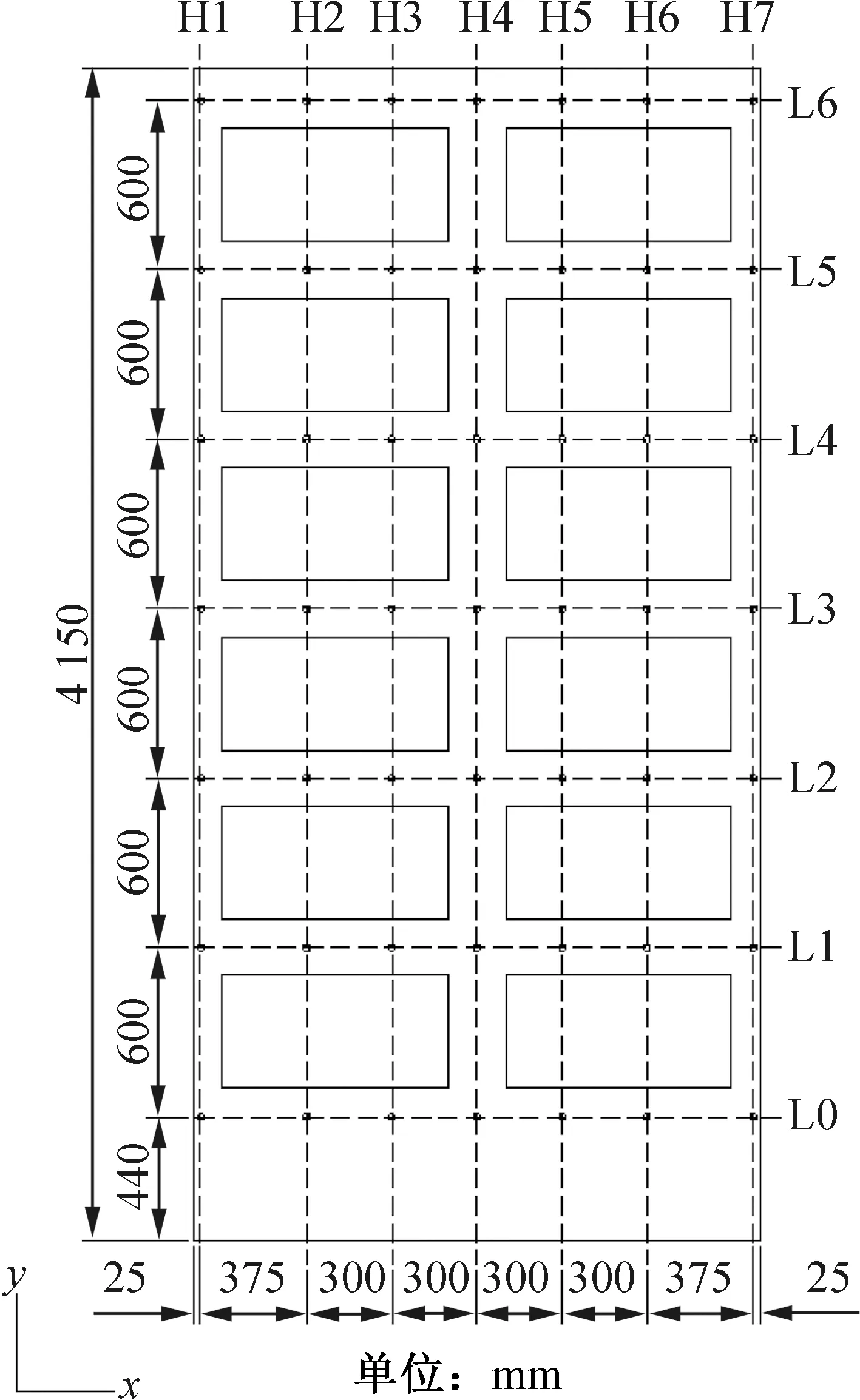
图4 监测点布置
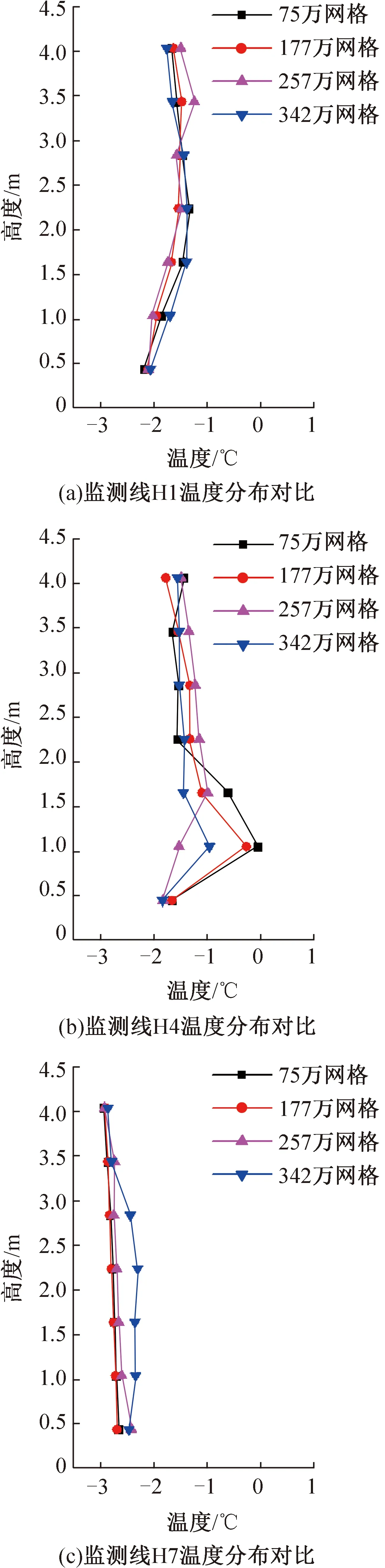
图5 网格独立性验证
3 模型验证
采用数值模拟和实验研究相结合的方法,研究送风参数(送风温度和送风速度)对冷柜内气流组织分布的影响。为验证数值模拟结果的可靠性,取岩心冷柜零负载送风温度为-3 ℃,送风速度为4.2 m/s,用铜-康铜热电偶对冷柜内z=0.25 m截面上7×7=49个温度测点进行实测,将水平监测线L2、L4和L6的实测温度值与模拟值进行对比。图6所示分别为零负载情况下,水平监测线L2、L4和L6实验值与模拟值温度对比。由图6可知,实验值与模拟值变化趋势基本一致,拟合程度较高,温度差值较小。监测线L2上各点实验值和模拟值的最大温差均不超过0.6 ℃;监测线L4上x=0.025 m的位置实验值和模拟值的差值为1.5 ℃,其余各点温差均小于0.2 ℃,这是因为模拟时冷空气从右上侧入口处沿着右侧壁面向下贴附流动,气流到达冷柜底面导致射流运动轨迹受限,在惯性力和回风口负压的综合作用下,一部分空气会沿着冷柜左侧壁面流向回风口,一部分气流经两列岩心之间的空气流道流回顶部回风口处,由于康达效应和压力梯度的存在,使水平监测线L4上靠近左侧壁面处测点冷空气向冷柜内部卷吸,围护结构传热无法被快速带走,进而导致该处温度较高;而实验过程中,由于货架等支撑物的存在,在冷空气向下流动的过程中,部分冷量经分流被送至冷柜左侧,有效消除了由于壁面传热导致的温升,故导致该点模拟值与实验值相差较大。监测线L6上各点实验值和模拟值基本契合,最大温差均不超过0.3 ℃。综上所述,实验与模拟结果整体吻合度较好,该模型用于数值计算具有足够的可靠性,为模拟冷柜内气流组织提供了理论依据。
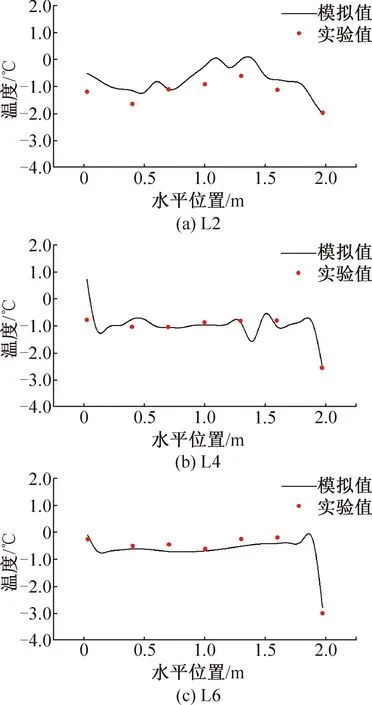
图6 零负载工况下水平监测线L2、L4和L6的温度模拟值和实验值对比
4 模拟结果分析
图7所示为当送风速度为4.2 m/s,送风温度分别为-3、-2、-1、0、1、2 ℃的工况下,冷柜满负载运行24 h,典型截面z=0.25 m上的温度分布。以图7(d)为例进行分析,气流组织形式为竖壁贴附射流,冷空气由顶部右侧送风口进入冷柜内后,与冷柜内空气进行混合,由于送风速度较大,与周围空气存在压力差,卷吸右列上下层岩心之间流道内的空气,冷空气与右列岩心以对流换热为主带走岩心内部热量进行冷却,右列6层岩心位于送风口处,为贴附射流起始段,冷空气与岩心接触面积较少,热交换较差,导致温度明显偏高,温度梯度较大,随着射流长度的增加,右侧壁面摩擦阻力存在,气流速度逐渐下降,温度逐渐升高,但射流扩散半径逐渐增大,冷柜下部岩心冷却效果明显优于上部。冷空气到达冷柜底部后,局部阻力增大,湍流程度加强,部分气流沿着地面向左侧壁面运动,碰撞左侧壁面后流动方向发生急剧偏转,在惯性力和回风口负压的综合作用下,沿着左侧壁面从底部向上运动,另外一部分气流经两列岩心之间流道到达回风口,因纵向空气流道之间存在较大的速度梯度,导致上下两层岩心之间区域形成多个小旋涡,强化对流换热。
综合对比分析可得,在24 h冷却时间内,送风温度对岩心的冷却效果影响较为显著,冷柜内部温度分布均匀性也存在一定差异,下半柜岩心的冷却效果明显优于上半柜。当送风温度为1 ℃和2 ℃时,冷柜内温度值较高,送风温度为2 ℃时热羽流和浮升力作用效果更显著,超过一半的岩心温度在4 ℃以上,未能达到岩心储藏条件;当送风温度低于0 ℃时,冷柜内部整体温度偏低,岩心虽被冷却至目标温度,但部分区域空气温度值已经低于柜内设定温度,随着运行时间的增加岩心温度值将低于最适宜的储藏温度;当送风温度为0 ℃时,冷柜内空气温度除送风侧均控制在2.5 ℃±1.5 ℃范围之内,完全符合岩心最佳储藏温度条件,冷柜内所有岩心被冷却至4 ℃以下,右列第六层岩心温度最高为3.4 ℃,温度分布较为合理,满足实际设计要求。
图8所示为送风温度为0 ℃,送风速度分别为3.5、4.2、4.7 m/s,冷却时间为24 h,冷柜z=0.25 m截面的温度分布云图。由图8可知,随着送风速度的增大,冷柜内换气次数增加,强制对流换热效果更显著,柜内的气流组织得到较好的改善,温度场分布更均匀合理,送风速度为3.5 m/s时,右列6层岩心温度较高,局部过热现象较明显,温度分布均匀性较差;送风速度增至4.2 m/s和4.7 m/s时,冷柜内部温度场分布得到显著改善,各层间温度梯度显著减小,局部过热问题得到有效解决,但送风速度过大导致射流距离增加,更多冷量被送至冷柜底部,以致柜内下半部分区域温度值已经低于适宜的储藏温度,送风速度增大的同时能耗也增加,综合考虑能耗和气流组织均匀性,4.2 m/s为最佳送风速度。
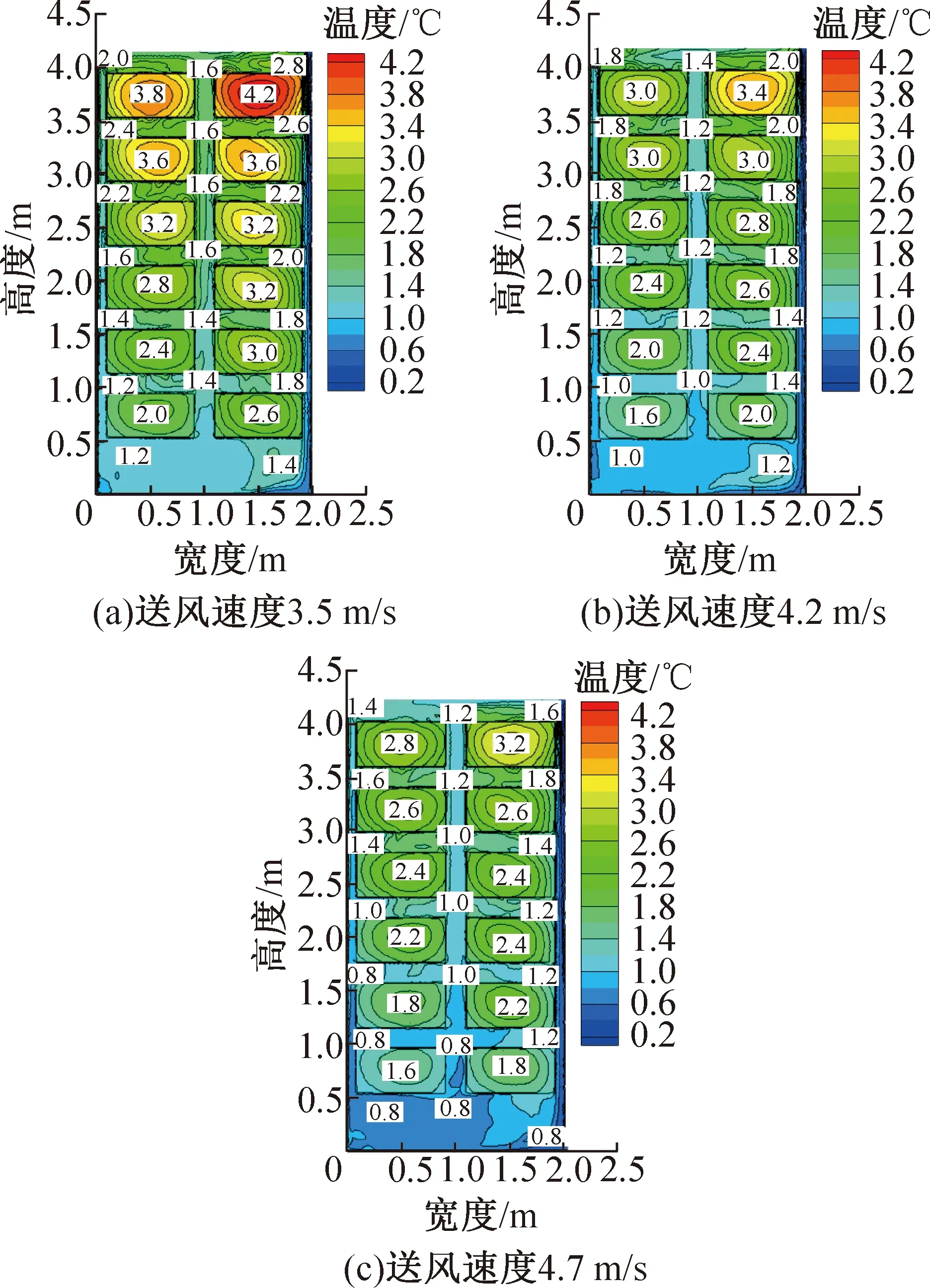
图8 不同送风速度,冷柜满载运行24 h,z=0.25 m截面温度分布云图
5 结论
本文结合某地质研究所自动化立体岩心冷柜建设项目,运用实验研究和数值模拟相结合的方法,研究岩心冷柜满载工况送风参数(送风温度、送风速度)对冷柜内部温度场的影响,得到最优送风参数以控制岩心储藏品质及冷柜整体能耗,研究工况下得到结论如下:
1)基于CFD数值模拟,取岩心冷柜零负载工况进行模型验证,各监测点温度实测值与模拟值分布规律趋于一致,吻合程度较高,偏差基本控制在0.6 ℃以内,表明数值模拟结果能够真实地反映冷柜内部温度场分布。
2)送风参数(送风温度、送风速度)对岩心冷柜内部温度场分布和岩心储藏品质影响较大。当岩心冷柜6层满载,送风速度不变时,降低送风温度,冷柜内部温度也随之降低,送风温度为0 ℃时冷柜温度场分布均匀合理,满足岩心储藏要求,为最佳送风温度。
3)当岩心冷柜6层满载,送风温度维持恒定时,增大送风速度能够优化冷柜内部气流组织,强化对流换热,有效解决局部过热问题,送风速度增大的同时,能耗也随之增加,送风速度由4.2 m/s增至4.7 m/s时,冷柜底部区域温度已低于最佳储藏温度,综合考虑节能减排降耗及气流组织均匀性,4.2 m/s为最佳送风速度。
4)综合对比分析不同送风参数下岩心冷柜内部气流组织分布规律,得到温度场分布均匀合理时的最优送风参数为送风温度0 ℃,送风速度4.2 m/s,为岩心冷柜工程实践提供理论支持。

