两相喷射器喷嘴距的优化设计及CFD分析

龙俊安 宋 霞 施骏业,2 陈江平,2

(1 上海交通大学制冷与低温工程研究所 上海 200240； 2 上海市高效冷却系统工程技术研究中心 上海 200240)

制冷空调系统在能源消耗中占比日益增大，制冷系统的节能问题备受重视。为提高制冷系统能效，可以采用喷射器来减少节流过程的能量损失。喷射器可将高压流体在节流过程产生的动能转化为低压流体的压力能，从而减小压缩机功耗，提高制冷循环的性能系数(coefficient of performance, COP)。对于R134a汽车空调，使用喷射器可使系统COP提高5%，对于跨临界CO2汽车空调，可提升10%～20%[1]。日本Denso公司已将喷射器用于冷藏车，COP提高了50%[2]。M. Haida等[3]将喷射器用于CO2商用冷冻系统，综合能效提高7%。

喷射制冷系统性能提高的关键在于喷射器的尺寸设计。其中，喷嘴出口位置，简称喷嘴距，对喷射器性能影响较大[4]。一些学者[5-6]研究表明，给定工况下存在最佳的喷嘴距使喷射性能最佳，增加或减少该值均会影响喷射性能，但上述研究均未揭示其机理。

最优喷嘴距通常根据实验[7-8]或计算流体力学(computational fluid dynamics, CFD)模拟[9]来确定。杜彦君等[10]采用经验关联式来设计喷射器的喷嘴距，但未解释关联式中的经验系数选取的依据。Chen Hongjie等[11]采用射流积分法，推导出最佳喷嘴距的经验公式，最佳喷嘴距的预测值与实验相比误差不超过±15.85%，但所用的经验公式依赖于射流速度、温度分布的经验数据。

本文结合湍流伴随射流理论，提出一个基于射流发展的喷射器喷嘴距优化设计准则，利用CFD模型分析不同喷嘴距下射流的发展及其对喷射性能的影响，验证上述设计方法的准确性。最后，本文提出用于预估最优喷嘴距的关联式。

1 基于射流发展的喷嘴距设计

1.1 两相喷射器的引射过程

图1所示为采用两相喷射器的制冷系统原理。压缩机排出的高温高压制冷剂经过气冷器或冷凝器冷却后进入喷射器，通过喷射器的喷嘴节流变为两相制冷剂。节流过程中部分膨胀功转化为主流的动能。高速主流卷吸来自蒸发器的引射流，并将动能传递给引射流，最后混合流体减速升压，实现膨胀功回收。混合流体经过气液分离器后，气体回到压缩机，而液体进入蒸发器，完成循环。

由图1可知，引射流来自蒸发器，引射压力即蒸发压力。对喷射器的设计而言，系统的目标制冷量决定了喷射器的目标引射流量。因此，本文讨论的喷射器喷嘴距优化设计以给定引射流量ms为前提，优化目标是喷射器升压最大化。升压定义为喷射器出口压力与引射压力的差值，即：

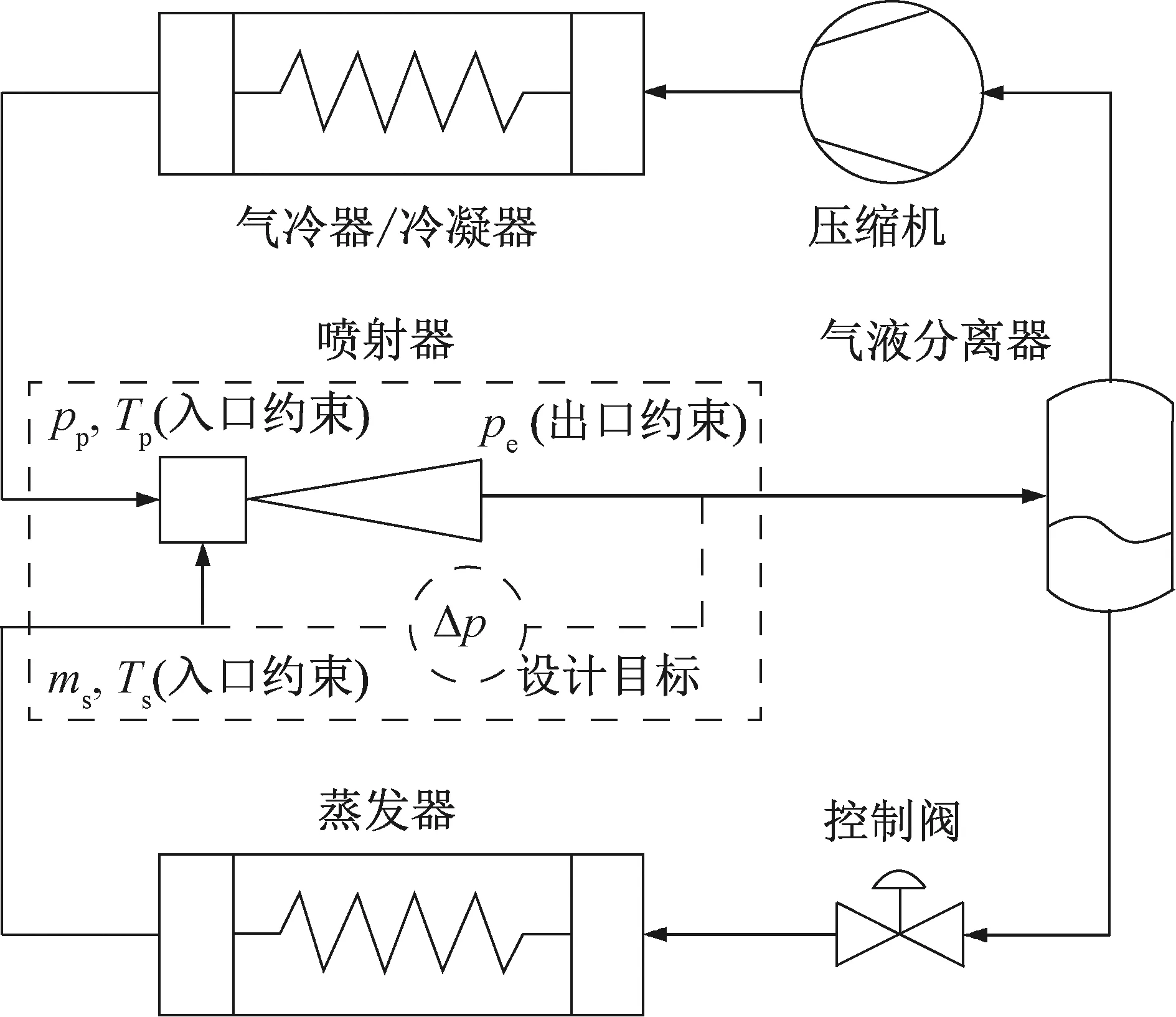
图1 两相喷射制冷系统原理

Δp=pe-ps

(1)

喷射器的喷嘴出口到等截面混合段的距离称为喷嘴距(nozzle exit position, NXP)。喷嘴距对两股流体的引射和混合过程有较大影响，从而对喷射器的结构优化设计和性能提升十分重要。图2所示为喷射器的引射过程。

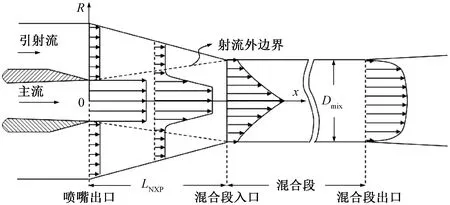
图2 喷射器内射流发展示意图

根据湍流伴随射流理论[12]，管内湍流伴随射流的发展将经历两个主要阶段：第一阶段，也称为射流起始段，两股流体混合前在各自的流道出口处速度是均匀的，随着两股流体的混合，速度均匀分布的射流核心区半径逐渐减小直至消失，与此同时，射流边界层逐渐向径向延伸；第二阶段，称为射流基本段，两流体持续发生径向动量交换，速度分布改变，直到速度分布满足圆管湍流的对数分布律，此时混合完成。

1.2 喷嘴距优化设计准则

陈亮等[13]认为，主流卷吸引射流过程的终止条件为射流外边界层的纵坐标等于混合段半径，并根据此条件结合射流积分法求解喷射器的引射流量。但如前所述，喷射器的尺寸设计应将引射流量作为已知条件。根据这一前提，本文提出喷嘴距的设计准则，即：在一定的引射流量下，当射流外边界层的半径等于混合段半径时，射流行进的距离即为最佳喷嘴距，用公式表示为：

Rex|x=opt,NXP=Rmix

(2)

式中：x代表到喷嘴出口截面的距离，x=0为喷嘴出口，如图2所示。式(2)的另一种解释：在混合流体进入混合段时，射流外边界刚好到达混合段内壁面，此时的喷嘴距为最优值。

2 喷嘴距优化设计的CFD分析

2.1 数学模型

利用ANSYS Fluent建立两相CO2喷射器的非平衡模型，用于量化分析上述喷嘴距的设计方法。流动的控制方程由两相混合物的质量、动量和能量守恒方程组成：

(3)

(4)

(5)

两相中，气相体积分数的输运方程为：

(6)

两相CO2喷射器的非平衡相变过程包括空化相变和沸腾相变。空化相变采用A. K. Singhal等[14]的全空化模型，沸腾相变采用V. P. Carey[15]的沸腾相变关联式：

(7)

(8)

本文使用的CFD模型已经过实测数据验证[16]，在pp=6.6～10 MPa、Tp=295～315 K的工况范围内，主流流量和引射压力的计算值与实测值的误差分别在6.5%和5%以内，故认为该模型可信度较高。

2.2 喷射器几何模型与仿真工况

利用ANSYS ICEM CFD对喷射器建模，将模型简化为二维轴对称，如图3所示。

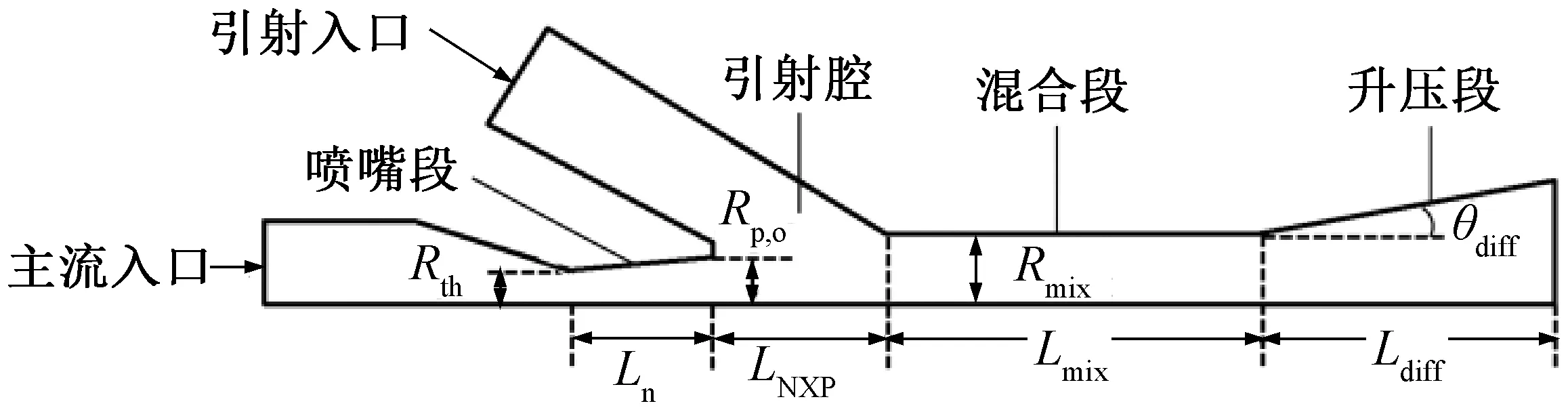
图3 喷射器尺寸结构

用于分析上述喷嘴距设计方法的两相CO2喷射器几何尺寸如表1所示。

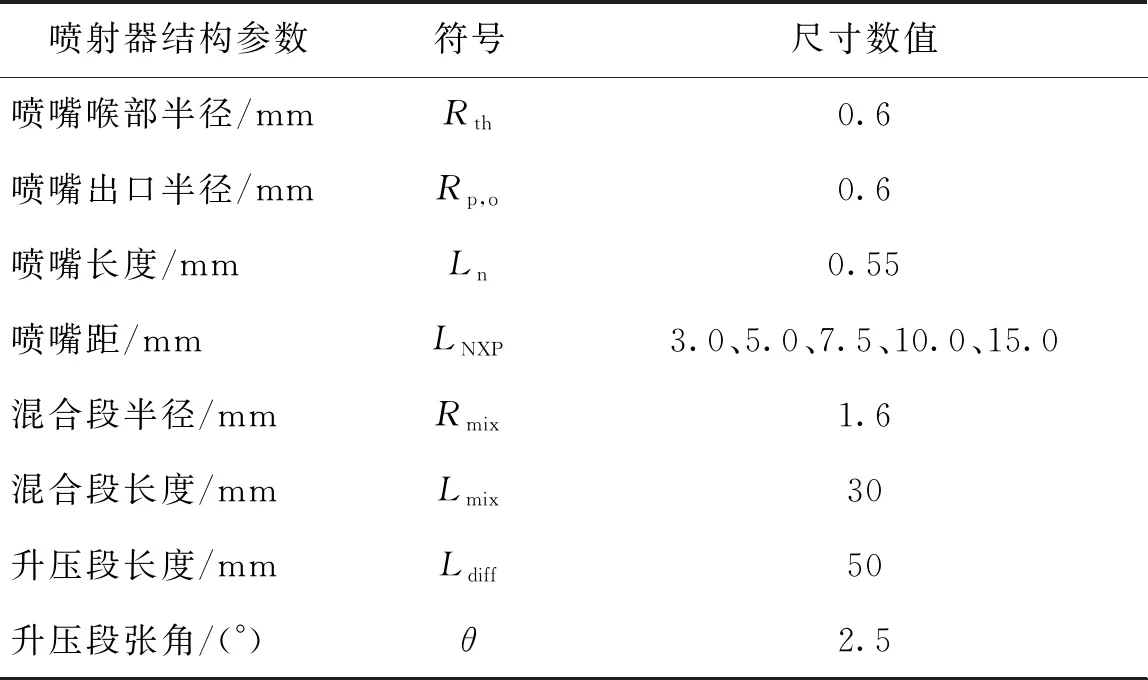
表1 用于CFD分析的喷射器尺寸

计算时，进出口约束条件如图1所示，本文讨论的工况为：pp=9.69 MPa,Tp=315 K,ms=0.016 7 kg/s,Ts=288 K,pe=4.88 MPa，在已验证的工况范围之内，引射压力ps和主流流量mp由CFD求解得到。

3 计算结果与分析

3.1 不同喷嘴距下性能对比

控制其他条件不变，当喷嘴距分别为3、5、7.5、10、15 mm时，喷射器升压性能如图4所示。当喷嘴距小于等于5 mm时，喷射器升压性能随喷嘴距的变化不显著。当喷嘴距大于5 mm后，随着喷嘴距的增大，喷射器升压性能迅速衰减。由此可知5 mm为当前工况和尺寸下的最佳喷嘴距，相对15 mm时提升46.8%。

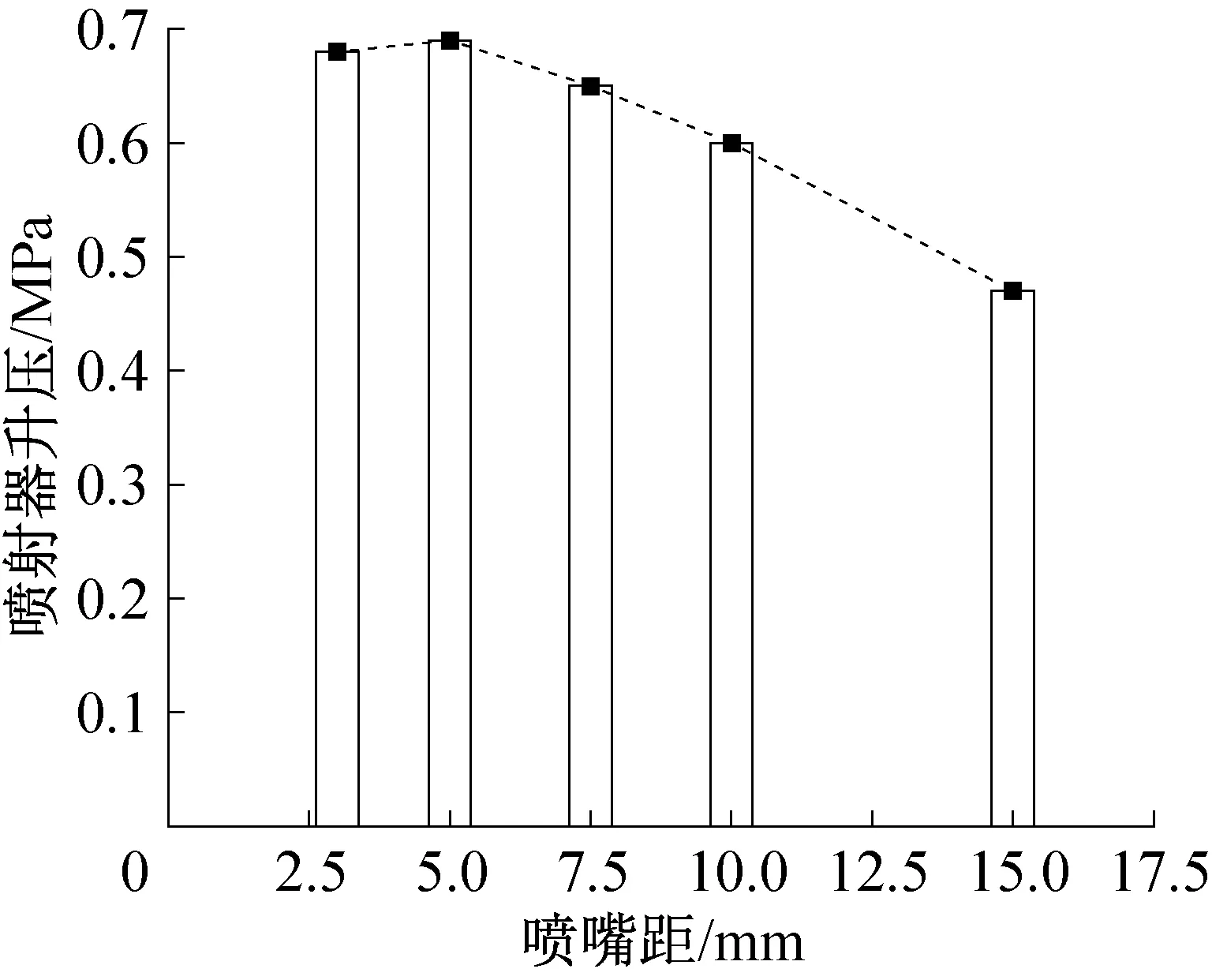
图4 不同喷嘴距下喷射器的升压性能

3.2 射流速度分布

图5所示为不同喷嘴距下从喷嘴出口到混合段内的速度分布云图。喷嘴出口处速度达到最大，射流边界在引射腔内沿径向扩展，射流核心区逐渐衰减，在等截面混合段内部才完全消失，说明射流发展第一阶段一直持续至混合段内。随着喷嘴距的增加，射流核心消失的地方越接近混合段入口。

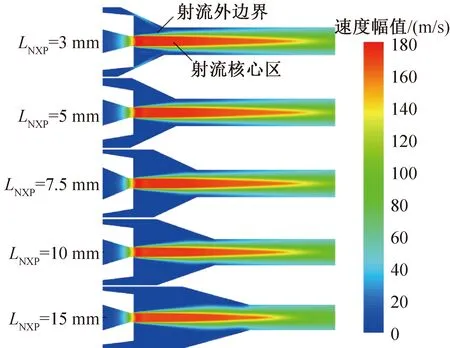
图5 不同喷嘴距下喷射器内部速度云图

图6所示为不同喷嘴距下从喷嘴出口至混合段入口处的流线图。当喷嘴距为3 mm和5 mm时，引射腔和混合段内的流线分布较为光顺，仅在喷嘴出口靠近壁面处存在一定的弯折，这是主喷嘴自身壁厚导致。当喷嘴距为7.5～15 mm时，混合段入口前端的引射腔壁面附近出现明显的涡流区。

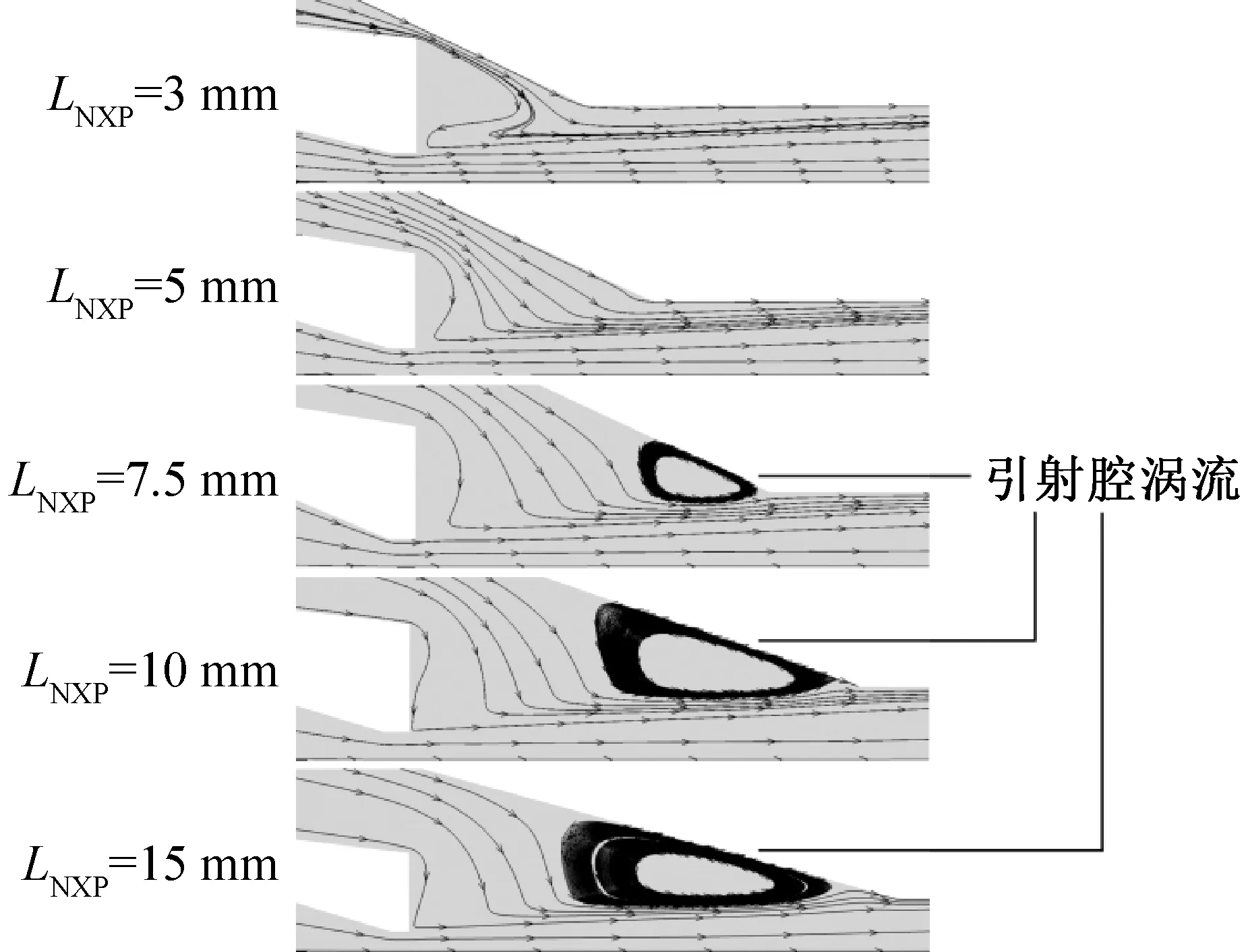
图6 不同喷嘴距下引射腔内流线图

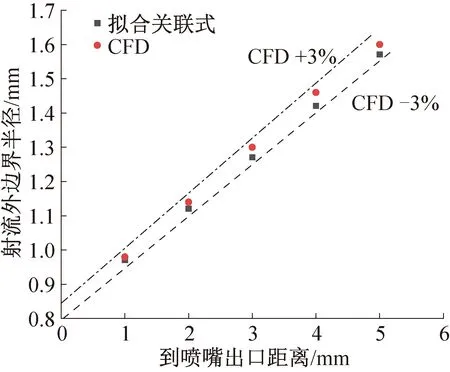
为进一步分析不同喷嘴距下性能差异和引射腔涡流区的形成原因，取喷嘴距为5 mm和10 mm时喷射器的射流速度分布进行分析。将喷嘴出口至混合段入口之间等间距取5个截面，并绘制速度沿径向的分布曲线。图7所示为喷嘴距为5 mm时，到喷嘴出口距离x分别为1、2、3、4、5 mm截面上的速度分布。图中射流外边界所在位置用虚线标示。在x=1 mm截面上，射流外边界发展到距离轴心约1 mm处，其半径Rex小于混合段半径1.6 mm，即满足Rex=0.98 mm

图7 喷嘴距5 mm时，不同截面上的射流速度分布

图8所示为喷嘴距为10 mm时，距离喷嘴出口分别为2、4、6、8、10 mm截面上的速度分布。图中射流外边界所在位置用虚线标示。当x=2～4 mm时，射流外边界层的半径为1.14～1.46 mm，未超过混合段半径。随着射流发展，当x≥6 mm时，射流外边界半径已超过混合段半径。由此导致的现象是：在混合段入口(x=10 mm)，只有部分射流能进入混合段，而超出混合段半径部分的外围射流将撞击在引射腔的斜壁面上，并形成涡流区而无法进入混合段，如图6中喷嘴距为7.5～15 mm时的流线图所示。当x=6 mm和x=8 mm时，射流边界外侧的引射流速度有一定程度的上升，这正是壁面上的涡流导致。这种漩涡会引起射流能量耗散，最终导致喷射器性能下降。因此，喷嘴距7.5～15 mm下的喷射器性能比5 mm时均有所下降，且喷嘴距越大，涡流区越明显，性能损失越严重。这一现象与张西平等[9]通过可视化实验观察到的结果相似。

图8 喷嘴距10 mm时，不同截面上的射流速度分布

当喷嘴距为3 mm时，喷射器的升压性能比5 mm时下降1.5%。这时因为射流进入等截面混合段时，射流边界还未发展到混合段壁面，主流卷吸引射流的过程有一部分是在混合段内完成的。这就导致射流发展的第二阶段略微延迟，混合段的有效长度略微减小，流体内部动量交换不够充分，最终导致喷射器性能略微下降。

3.3 最优喷嘴距关联式

由图7所示的射流速度发展规律可知，在引射腔不出现涡流的情况下，射流外半径与射流行进距离近似呈线性关系。实际上，射流的这种规律具有普遍性，称为射流速度分布的自模性[12]。从这一特性出发，结合喷射器的结构特点，利用本文案例结果拟合射流外半径Rex的经验公式，即：

(9)

式中：x为射流行进(出口)距离，mm；pp,o/ps,o表示喷嘴出口激波或膨胀波对速度分布的影响；C(up,o-us,o)表示射流外半径随x的增长率，两股流体速度差越大，射流边界增长越快。由本文5 mm案例可得经验系数C=8.824×10-4s/m。图9所示为由式(9)预测的不同截面上射流外半径Rex与CFD结果的对比，相对误差不超过3%。

图9 关联式与CFD预测的射流外半径对比

由式(2)可知，当Rex取混合段半径Rmix时，射流行进距离即最优喷嘴距，则由式(9)可得最优喷嘴距的经验公式：

(10)

在本文讨论的工况下，由式(10)计算的最优喷嘴距为5.21 mm(pp,o=5.1 MPa,ps,o=4.2 MPa,up,o=175 m/s,us,o=5 m/s)，CFD模拟结果为5 mm，相对误差为4.2%。当工况和主喷嘴尺寸给定后，式(10)可用于工程上快速预估最优喷嘴距。

4 结论

本文根据湍流射流发展规律，提出了一个喷射器喷嘴距的设计准则，利用CFD模拟对比不同喷嘴距下两相CO2喷射器的性能，通过分析射流速度分布揭示喷嘴距对两相喷射器性能的影响机制，并验证了喷嘴距优化设计准则的正确性，最后结合本文案例提出了最优喷嘴距的关联式，得到结论如下：

1)在一定的引射流量下，当射流外边界层的半径发展到与混合段半径相等时，射流行进的距离即为最优喷嘴距。

2)对喷嘴距分别为3、5、7.5、10、15 mm的两相CO2喷射器的案例研究表明，5 mm下升压性能最优，为0.69 MPa，相对15 mm时提升了46.8%，此时射流的发展规律正好符合上述设计准则。喷嘴距大于最优值时，射流外边界超过混合段半径，部分外围射流将撞击引射腔壁面而无法进入混合段，并在引射腔壁面形成涡流区，导致射流动能耗散，性能下降。而喷嘴距为3 mm时，小于最优值时，引射过程在混合段内完成，混合段有效长度减小，升压性能比最优时下降1.5%。

3)结合本文案例拟合了射流外边界随出口距离变化的关联式，与CFD相比误差不超过3%，并由此得到最优喷嘴距的经验公式，其预测结果相对CFD的误差为4.2%，工程上优化设计喷嘴距时，可用于计算初始值。

符号说明

m——流量，kg/s

p——压力，MPa

x——轴向坐标，mm

T——温度，K

ρ——密度，kg/m3

u——速度矢量，m/s

τ——应力张量，N/m2

e——比总能，kJ/kg

α——气相体积分数

C——经验系数,s/m

k——湍动能，J/kg

σ——表面张力，N/m

M——相对分子质量，kg/kmol

G——气体常数，J/(kg·K)

R——半径，mm

L——长度，mm

θ——角度，(°)

下标

p——主流

s——引射流

e——喷射器出口

o——喷嘴出口

m——混合相

v——气相

l——液相

ex——射流外边界

sat——饱和态

mix——混合段

NXP——喷嘴距

opt——最优值

cav——空化相变

boil——沸腾相变