基于变导纳柔顺策略的康复机械臂示教研究

程 杨 潘尚峰 孙江宏

（清华大学机械工程系，北京 100086）

脑卒中具有高致残率及高复发率的特点，约3/4的存活者存在不同程度的残疾，且5 年复发率高达41%[1]，给家庭和社会带来极大的负担。积极规范的康复治疗可以在最大程度上改善脑卒中预后，提高患者的生活质量[2]。康复机器人可以部分解决我国目前康复医疗资源不足的问题，它们大多储存内置一些标准的康复动作库，通过被动、主动康复等模式，辅助病人康复治疗。但由于不同病人、不同阶段的特异性，康复医师会对此开具具有针对性的“运动处方[3]”，而这些动作不存在于标准康复动作库，所以开发示教训练十分必要。利用示教模式，可以将康复机器人的康复训练与康复医师的临床经验相结合，从而针对具体病人的实际情况，提供科学、高效的康复训练计划，显著改善康复治疗的效果[4]。

与采用人体动作捕捉设备[5]、双目视觉测距[6]等方式采集康复示教动作相比，穿戴拖动示教不需要额外的采集设备，能够降低系统的复杂性。康复医师穿戴康复机械臂进行康复动作示教，机械臂在受控状态下完成跟随动作，在线保存轨迹数据，储存康复动作，从而完成示教。在实际应用时通常采用Hogan N[7]提出的阻抗控制方法，使康复机械臂具有柔顺特性，完成这一人机交互过程。

康复示教过程是动态时变的，固定参数的导纳控制模型难以充分反应人机交互的特征，且随着关节活动度的不同，人体关节的刚度也会发生改变。为保障拖动示教过程的安全性及跟随性，机器人需要具有可变的柔顺性[8]。变导纳控制算法有模糊变导纳、自适应变导纳以及智能控制策略，如结合强化学习、神经网络等方法进行变导纳控制[9]。付兴[10]等利用余弦相似度，模糊辨识机器人的状态，如启动、加速、高速稳定运动及减速等，不同状态配以不同的阻尼参数，并通过试验验证了所提出控制方法的有效性，但其运动轨迹较为简单，普适性较差。吴青聪[11]等利用模糊滑膜导纳控制算法，改变系统导纳参数，增强人机交互的柔顺性，提高系统的舒适性。郝向阳[12]利用李雅普诺夫第二法构建系统自适应控制模块，降低了拖动过程中的波动和干扰。杜志江[13]等提出基于模糊强化学习的变导纳人机交互控制模型，结合个人操作因素，并运用于微创外科手术机器人的姿态调整，取得一定的成果。王飞[14]等提出根据环境刚度变化在线调节导纳阻尼参数的方法，使得机械臂牵引跟踪轨迹更加平滑，但机械臂为3 自由度，动力学模型耦合度较低。

针对示教过程中康复机械臂由于柔顺性不足导致的随动效果不佳的问题，本文设计了在关节空间内结合力矩微分项的导纳控制器，并结合双曲正切函数设计了改进的变导纳控制策略，提高机械臂的柔顺性，以期望获得良好的跟随效果。

1 康复机械臂介绍

为实现穿戴康复示教的目的，本文采用的康复机械臂如图1 所示。康复机械臂具有4 个主动旋转关节，1～3 号关节由3 个旋转轴相交且相差60°的电机组成，用于模拟人体肩关节的运动自由度，4号关节用于模拟人体肘关节的自由度。这4 个自由度可实现人体上肢的肩部外旋/内旋、外展/内收、屈曲/伸展及肘部屈曲/伸展功能。每个电机的输出端均通过输出杆安装一个BONGSHIN CDFS-100kgf拉压力传感器，用于间接测量人机交互力矩（图2为以电机3 为例，拉压力传感器安装示意）。

图1 康复机械臂实物图片

图2 拉压力传感器安装图示

参照实际使用的材料及零部件尺寸建立康复机械臂的SolidWorks 模型，在肩心位置和每个自由度的旋转中心沿电机输出轴方向，建立了右手坐标系，并将得到的标准Denavit-Hartenberg 参数汇总在表1 中。

表1 机械臂标准DH 参数表

2 导纳控制系统设计

2.1 导纳控制原理及改进

结合本文采用的康复机械臂的特点，采用关节空间的导纳控制。

根据导纳控制的基本思想，将人体作为作业环境，则关节空间内，人体上肢与康复外骨骼机械臂的导纳模型如图3 所示。其中，τi是关节处的人机交互力矩，Ji为转动惯性系数，bi为阻尼系数，ki为刚度系数，ke为人机交互刚度系数。

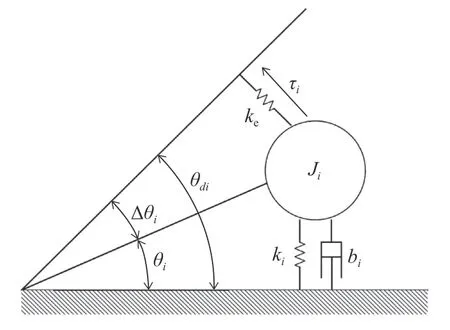
图3 转角形式导纳控制原理

则有：

在示教过程中，康复机械臂处于自由运动状态，故而设置ki=0,i=1,2,3,4 ，同时记Δ θi=θdi-θi，式（1）等效为：

为更好地改善人机交互效果、提高示教跟随性及柔顺性，引入人机交互力矩的微分项，从而增加导纳控制器对人机交互力矩的敏感性并提高跟随精度，对控制方程式（2）修正为：

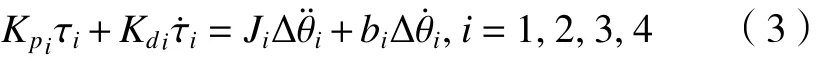
对式（3）进行拉氏变换，得到系统导纳控制器的传递函数为：

对于整个系统而言，其示教控制算法流程框如图4 所示。

图4 示教控制算法流程框图

图4 中，位置内环采用的是虚拟分解理论控制（virtual decomposition control,VDC）方法。使用者穿戴机械臂进行康复动作，通过拉压力传感器采集到人机交互力，再结合输出杆长、电机输出转矩及各关节重力补偿矩，计算出实际人机交互力矩，输入到导纳控制器中，得到机械臂各关节下一周期期望位置。结合反馈的机械臂各关节现有角度，作为位置内环的输入，计算得到各关节所需的输出扭矩，从而驱动机械臂到达所需位置。

2.2 基于双曲正切函数的变参数导纳控制算法

本文的变导纳算法利用了双曲正切函数（tanh），这是一种在神经网络中常见的标准激活函数，具有完全可微分、反对称、对称中心在原点的优势，保证了导纳参数调整的平滑性。

在实际人机交互过程中，需要关注的是交互力矩的绝对值大小，与方向无关，且双曲正切函数的值域是(-1,1)，为实现变导纳控制，对双曲正切函数进行一定的变形处理。引入调整系数及对称处理，得到新的调整函数 tanh(x)：

tanh(x) 及 tanh(x)的函数图像如图5 所示。通过调整参数m、n的值，可以对 tanh(x)的值域及集中度进行调整。m越大， tanh(x)的最小值越小。n越大，tanh(x)越集中，在0 附近的变化越快。

图5 tanh(x)及tanh(x)的函数图像

在具体的变参数导纳过程中，转动惯性系数J会同时引起系统固有频率及阻尼的快速变化，其可调整的范围有限，且会影响系统的整体稳定性[8]。在本文中采用对阻尼系数b进行调整。

当人机交互力矩变大时，降低导纳控制器的阻尼系数，可以使康复机械臂快速提供较好的顺应性，并改善系统的柔顺性；当人机交互力矩变小时，导纳控制器的阻尼系数较大，可以保证系统的稳定性及较高的位置控制精度。

利用调整函数 tanh(x)，则有

其中：bmaxi为bi的最大值，m为范围调整参数，可以调节bi的最小值，n为变化率调整参数，用于调节bi的变化率。

根据二阶系统模型的特性，为保障系统的稳定性，导纳控制器还需要满足以下3 个条件：

在示教训练中，ki=0;i=1,2,3,4，则上述条件中，条件1、2 显然满足，条件3 等效有：

所以m∈[0,1)，且需满足式（8）。

3 仿真平台搭建及结果分析

3.1 仿真平台搭建

为验证提出的改进变导纳控制器的有效性，利用机械臂SolidWorks 模型（图6），采用Adams 与MATLAB/Simulink 联合仿真，进行画圆示教实验。

图6 机械臂SolidWorks 模型

先将SolidWorks 中配置有质量属性的机械臂模型导入Adams 中，之后在4 个关节处创建旋转运动幅，添加对应的旋转运动驱动，定义扭矩、角速度等矢量方向。考虑到关节处摩擦力分析较为复杂，仿真时做了简化处理。在Adams 中各旋转运动幅设置最大静摩擦因数为0.3、动摩擦因数为0.1。

利用Adams 中的Controls 插件，定义系统输入为4 个旋转幅的驱动扭矩（图7 中tourque1～4），输出为4 个旋转副的旋转角度及角速度（图7 中q1～q4_dot），导出为m 文件，并在Simulink 中打开，如图7 所示。

图7 Adams 导出的控制子模块

为引入人机交互力矩信息，假设环境刚度为ke，即康复机械臂实际运动角度与使用者的期望角度产生偏差时，为修正偏差，使用者在各对应关节施加的交互力矩有

结合控制流程框图4，搭建图8 所示的Simulink图，其中棕色部分为Adams 导出的机械臂m 文件，用于进行动力学仿真；绿色的部分为系统的内部位置环，采用虚拟分解理论进行实现，具体如图9 所示，输入量为下一周期期望角度及当前周期机械臂实际运动角度，输出为各关节所需驱动力矩，驱动机械臂到达期望位置；蓝色部分为系统的导纳控制部分，q1_r,q2_r,q3_r,q4_r 为使用者的期望角度。具体到adimittance模块内部，由4 个各关节导纳控制组成，以关节1 为例（图10）。q1_r 为期望角度，q1_v 为当前位置，两者差值乘以环境刚度ke，结合式（9）可以得到使用者的仿真输入力矩TOL1，作为导纳模型的输入，在variable_admittance 模块中，利用式（7），改变当前周期的阻尼参数b1，最终得到机械臂下一周期所需到达的位置q1_d。

图8 系统仿真Simulink 图

图9 位置环VDC 控制

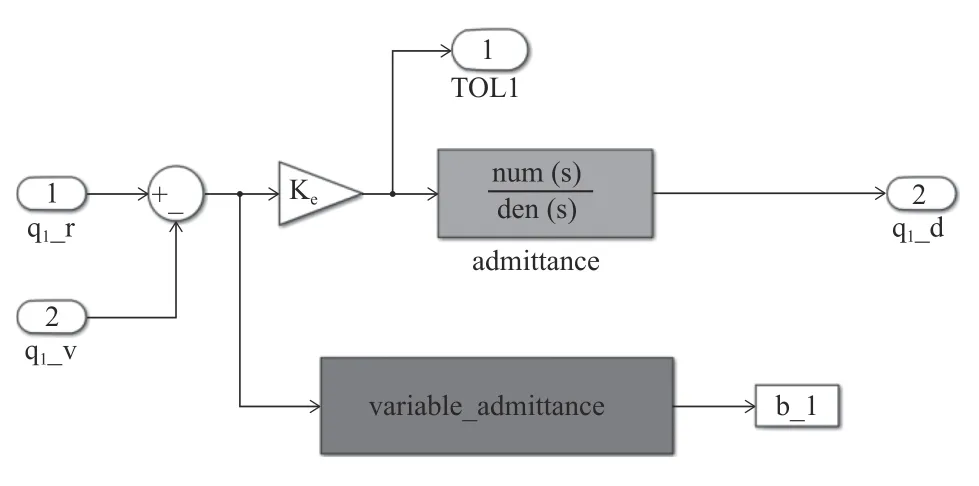
图10 改进变导纳控制器

仿真实验期望动作轨迹采用笛卡尔空间下均匀画圆，利用机械臂逆向运动学解出q1_r,q2_r,q3_r,q4_r 作为所需轨迹输入，结合Adams 与MATLAB/Simulink进行联合仿真。仿真实验采用的主要参数为：

3.2 实验结果与分析

实验结果如图11～13 所示。图11 为3 种方法下的机械臂示教跟随效果。在起始时有些许超调，之后康复机械臂跟随性较好。

图11 仿真实验机械臂末端位置

图12 为具体的机械臂末端位置在x、y、z这3个方向上的误差，由于是在xz平面内画圆，故而y方向误差较小。误差数据整理如表2 所示。在最大误差绝对值方面，除起始时，改进导纳及改进变导纳控制器在x方向超调量较大外，后续过程中，两种方法均可降低常规导纳控制的跟随误差；在平均绝对值误差方面，改进导纳控制可以将常规导纳的误差降低到近一半，而改进变导纳控制可以进一步降低机械臂的跟随误差，将机械臂末端位置跟随精度控制在2 mm 以下，提高示教过程精度。

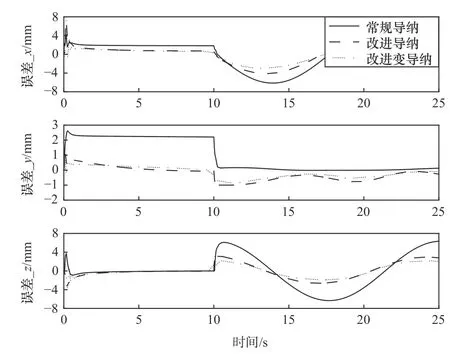
图12 仿真实验机械臂末端位置误差

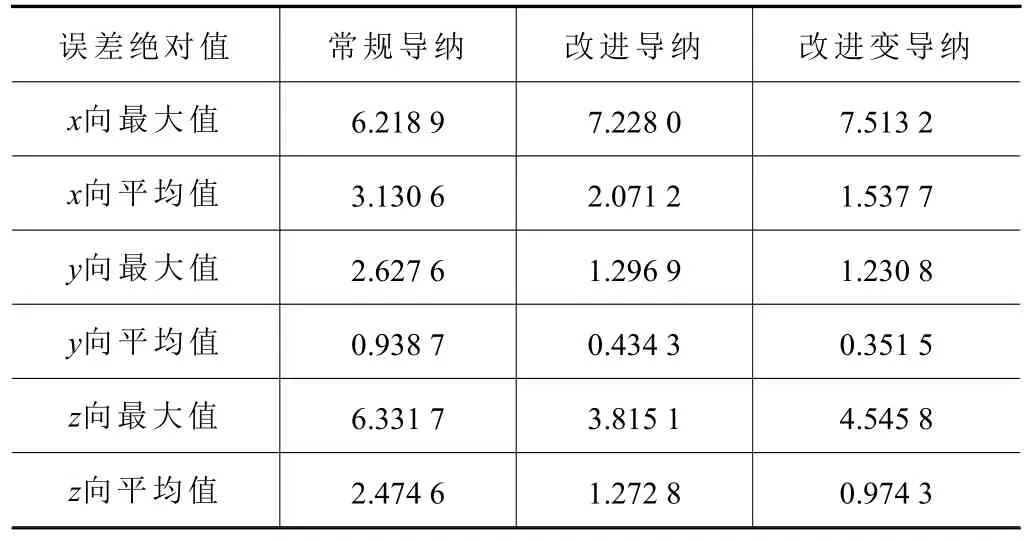
表2 仿真实验误差分析 mm

图13 反映的是3 种控制方法下，各关节人机交互力矩的大小，整理分析数据见表3。在力矩峰值方面，改进变导纳控制可以很好地降低力矩峰值，与常规导纳相比，其关节1 交互力矩峰值降低45.30%，关节2 交互力矩峰值降低33.07%，关节3 交互力矩峰值降低10.99%，关节4 交互力矩峰值降低19.67%，大大减少了示教过程中使用者的负担，提高了人机交互的舒适性；在人机交互力矩平均值方面，改进变导纳的各关节平均交互力矩不到常规导纳的一半，也进一步说明，在整个示教过程中，改进变导纳方法更加轻便。

图13 仿真实验各关节人机交互力矩曲线

表3 仿真实验人机交互力矩分析 N·m

4 实物试验及结果分析

4.1 试验装置及过程设计

为进一步验证上述理论的有效性，对康复机械臂系统进行实物画圆示教试验。利用实验室开发的康复机械臂，在手臂末端固接一只马克笔，白板上固定一个直径180 mm的参考圆（图14）。试验过程如图15 所示，实验者通过穿戴康复机械臂，利用末端马克笔在白板上参考画圆，每次重复画圆10 次。结合图2，试验时，穿戴者作用于机械臂，通过拉压力传感器采集数据，乘以输出杆的长度，再减去机械臂关节输出扭矩及各关节重力补偿力矩，得到人机交互力矩，作为导纳控制系统的输入。实验过程中，下位机通过串口上报上位机各关节角度及计算得到的人机交互力矩，上报周期10 ms。试验参数除Kd=0.3外，其余同3.1 节参数设置。采用常规导纳控制与改进变导纳两种方法进行穿戴康复示教试验。

图14 示教试验平台

图15 示教试验过程

4.2 实验结果及分析

利用机械臂正向运动学，将采集到的各关节运动角度转换为机械臂末端马克笔的空间位置。记录整理数据如图16～18 所示。

图16 常规导纳控制法示教实物试验画圆

图16和图17 分别是采用常规导纳控制方法和本文提出的改进变导纳控制方法穿戴示教画圆得到的结果。常规导纳方法的多次画圆之间重复性较低，且偏离参考圆较多。这一点也体现在表4 中。采用改进变导纳控制方法，降低了跟随误差的最大值，且与常规导纳控制方法相比，标准差降低11.46%，平均误差绝对值降低25.09%。这说明采用改进变导纳控制方法，使用者示教过程更加平稳，重复性较好，平均误差也大大降低。

图17 改进变导纳控制法示教实物试验画圆

表4 实物试验误差分析 mm

各关节的人机交互力矩如图18 所示，改进变导纳控制方法在整体上比常规导纳的力矩要小。分析人机交互力矩绝对值的特征信息汇总于表5。除关节1 两种方法的区别不大外，在关节2～4 方面，改进变导纳控制方法均在不同程度上降低了人机交互力矩绝对值的最大值、标准差及平均值，其中最大值方面以关节4 方面降的最多，降低了63.44%；标准差及平均值以关节2 方面降低最多，分别为23.27%及20.79%。结合输出连杆长度为65 mm，示教过程中，使用者作用于各关节的力不超过2.23 N，示教负担较小。

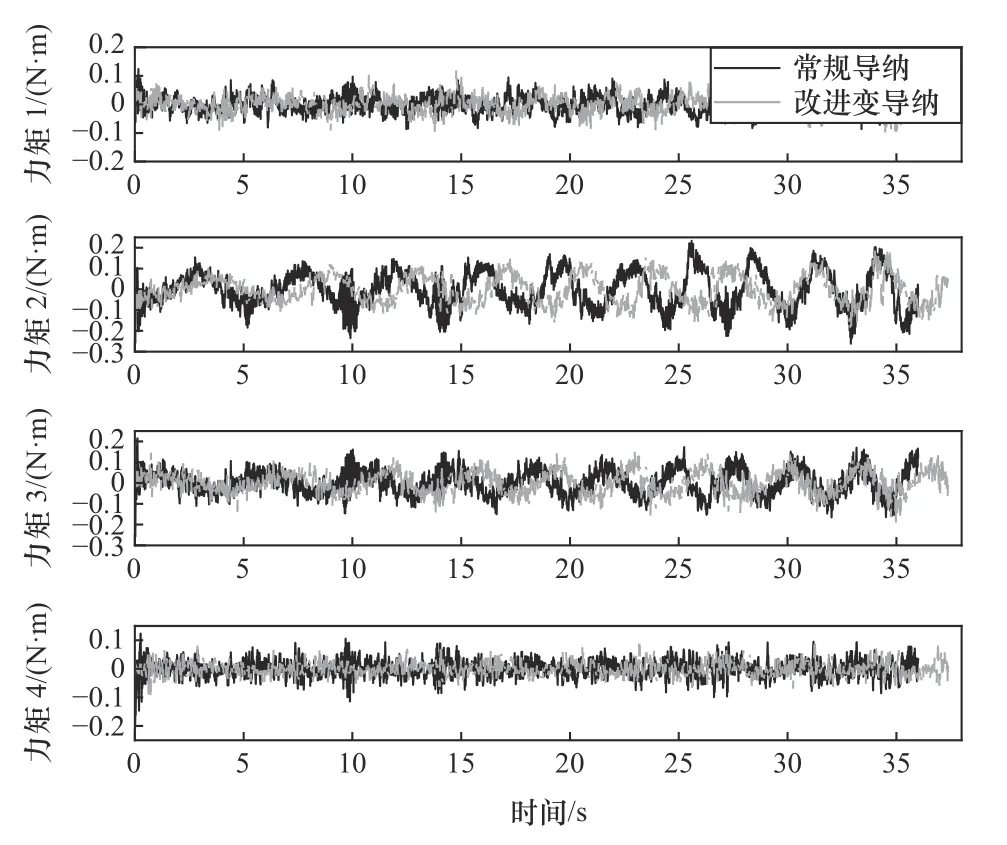
图18 实物试验人机交互力矩曲线

表5 实物试验人机交互力矩绝对值分析 N·m

尽管新提出的导纳控制器降低了常规导纳控制的跟随误差，但仍然有平均2.462 6 mm的误差。这主要有以下两个原因：

（1）机械臂杆长的放大作用。串联机械臂各旋转关节均安装有谐波减速器，系统具有一定程度的柔性，刚度较低，会导致位置内环的误差。本文采用的机械臂仅小臂杆长就有470 mm，如果关节位置误差精度控制在0.005 rad，转换到末端空间位置误差就有近2.35 mm的误差。

（2）本文采用的导纳控制器设计是基于关节空间的，但画圆时，使用者通过目光观察，接受到的画圆误差反馈是在笛卡尔空间下，其做力矩调整也是在x、y、z这3 个方向，而不是直接调整所需的关节角度，故而也会一定程度上增加系统的跟随误差。

但总体来说，本文提出的改进变导纳控制器，可以将示教试验画圆平均误差控制在2.5 mm 以下，能够满足康复示教训练的需求，便于康复机械臂后续功能的开发。

5 结语

（1）针对康复机器人示教过程中跟随效果不佳的问题，提出了关节空间下结合力矩微分项的导纳控制方法，并创新性地采用双曲正切函数实现变导纳控制器的设计，提高机械臂的柔顺性。

（2）利用康复机械臂的SolidWorks 模型，结合Adams 及MATLAB/Simulink 搭建了仿真实验平台，并进行画圆示教实验。仿真结果表明，提出的改进变导纳控制器可以降低示教跟随误差，实现较高精度的示教过程，且人机交互力矩也较小。

（3）画圆康复示教实物试验结果表明，本文提出的结合力矩微分项的双曲正切函数变导纳控制器能够很好地跟踪示教者的动作，重复性好，降低了人机交互力矩，提高了系统的柔顺性，改善了机械臂随动效果。