基于RPP 串联机构的固定式割胶机设计与仿真分析＊

高 锋 孙江宏② 何宇凡 李乃峥 高可可

（①北京信息科技大学机电工程学院，北京 100192；②清华大学机械电子工程研究所，北京 100084）

天然橡胶是不可替代的重要战略物资和工业材料，目前的人工割胶方式劳动强度大、技术要求高、工作效率低，远不能满足我国对天然橡胶的需求[1-3]。割胶工具是影响天然橡胶产量的决定性因素，因此通过现代科学技术实现割胶生产的机械化与智能化迫在眉睫[4-5]。

目前割胶设备主要以固定式割胶机为主[6-9]。张春龙等研制了一种基于三坐标轴的固定式割胶机，但框架结构只能对单一高度割面实施割胶作业，无法实现全方位割胶[10]。许振昆等基于圆柱坐标系发明的固定式割胶机，切割深度无法控制，不能保证橡胶树使用寿命[11]。吴米等结合割线特点研制的固定式割胶机，连接结构采用支点接触，易造成受力不均，设备稳定性无法保证[12]。张俊雄等发明了一种可实现下刀、行刀和收刀一体化的固定式割胶机，但需要操作者拉动滑座实现割胶作业，无法实现全自动割胶[13]。韩青江结合割胶技术难点设计的固定式割胶机，可设定不同割线斜度和切割深度，但无法实时控制[14]。

本文设计了一种新型固定式割胶机。该割胶机具有三自由度、可实现复杂空间曲线运动、满足不同切割深度以及割线斜度。同时该机构具有多输入多输出、非线性和位置时变等特点，故采用机器人理论将该机构等效成RPP 模型，对其进行运动学和动力学求解与仿真。

1 结构设计

1.1 人工割胶过程分析

割胶过程如图1a 所示，首先需标定前后水线的位置，入刀点在后水线上，收刀点在前水线上，割面开角为1/4 树周。在进行割胶工作过程中，工人手持胶刀，以入刀点为起点，沿割线自右下至左上切割树皮，使胶乳从割口处流出，以收刀点为终点，结束一次割胶工作。为保证橡胶树经济寿命，前后两次割线之间的轴向距离需要控制在1.3 mm 以内。

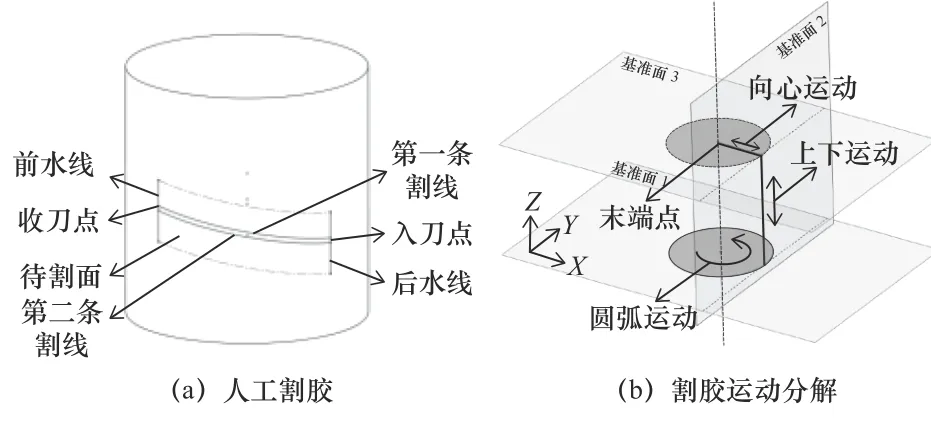
图1 割胶过程

在割胶作业过程中有割深、高度和弧度3 个重要指标。割深指树皮表面至割口的距离，由于橡胶树内部产胶层距离树皮表面约为5～6 mm，因此需要控制切割深度。高度指入刀点至收刀点沿树干轴向方向的距离，弧度指后水线至前水线沿橡胶树树皮所扫过的角度。割线斜度需控制在25°～30°，因此需要对高度和弧度进行控制[15-16]。

人工割胶过程中所产生的割线是一段近似圆柱螺旋线的复杂空间曲线。为了实现割线轨迹，可将人工割胶过程分解为3 个不同空间平面运动，如图1b 所示。

在图1b 中，垂直于树干轴心的径向运动可实现割深控制；沿树干方向的上下轴向运动可实现高度控制；绕树干轴心转动的圆弧运动可实现弧度控制。将径向运动、上下轴向运动以及圆弧运动组合，3 个不同空间平面的运动轨迹共同作用于向心运动的末端点，实现复杂空间曲线。

1.2 一种新型固定式割胶机结构设计

根据上述3 个不同空间平面运动及其运动关系，设计一种新型固定式割胶机，分为固定机构、圆弧轨道以及割胶工作模块3 部分，如图2 所示。固定机构将设备固定在橡胶树上；上顶板与下底板均安装有滚轮与圆弧轨道上的“凹”字型轨道配合，限制割胶工作模块的运动方式。割胶工作模块中的传动齿轮组、运动转轴和运动转轴两端的传动齿轮组成齿轮传动模块。

图2 固定式割胶机

传动齿轮组9、丝杠传动模块3和丝杠传动模块5 均可相对独立运动。传动模块通过传动齿轮组9 转动带动运动转轴10 转动，运动转轴10 两端各有一个传动齿轮8，传动齿轮8 与圆弧轨道上的内齿圈啮合带动割胶工作模块实现某一圆心角度的圆弧运动。丝杠传动模块5和丝杠传动模块3 可分别实现滚珠丝杠滑台模组中滑台的上下轴向运动以及径向运动。传动齿轮组9、丝杠传动模块5和丝杠传动模块3 分别通过上顶板与下底板以及L 型板2集成在一起，通过3 个传动模块空间运动的叠加实现胶刀的复杂空间曲线轨迹。

2 新型固定式割胶机理论分析

2.1 理论模型构建

通过机器人学对新型固定式割胶机的关键部件及部件之间的运动关系进行理论模型构建，如图3a所示。

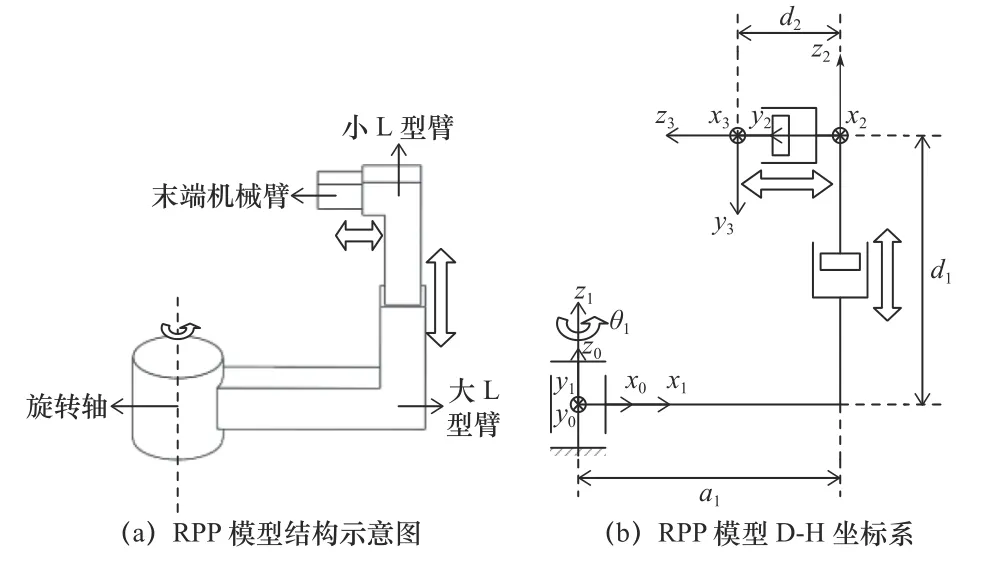
图3 RPP 串联机构

图3a 中RPP 串联机构共有3 个自由度，包括1 个转动副和2 个移动副，旋转轴带动大L 型臂进行转动，小L 型臂相对于大L 型臂可上下移动，末端机械臂相对于小L 型臂可向心移动。其中旋转轴和大L 型臂表示齿轮传动模块；小L 型臂和大L 型臂表示丝杠传动模块1；末端机械臂和小L 型臂表示丝杠传动模块2和胶刀模块[17]。

2.2 运动学模型求解

根据RPP 串联机构模型建立D-H 坐标系[18-19]，如图3b 所示，读取所有相邻连杆坐标系的D-H 参数，建立RPP 串联机构参数表，如表1 所示。

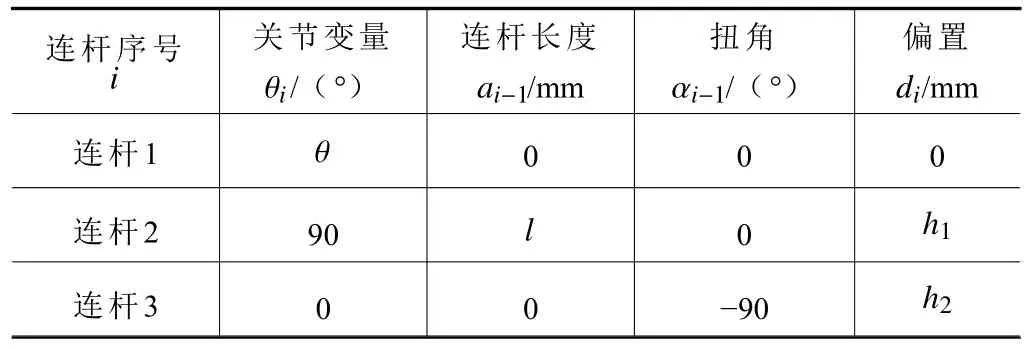
表1 RPP 串联机构D-H 参数表

将D-H 参数表中各行参数代入D-H 矩阵通式（1）中，得：

式中：i=1、2、3

2.3 RPP 型机械臂各关节运动学分析

不同尺寸的树围会形成不同的割线，但每条割线均是由圆柱螺旋运动叠加反复的向心运动合成。因此在工作空间范围内取一条理想割线，其中旋转角度为90°，割线斜度为25°，如图4 所示。

图4 理想割线

已知笛卡尔空间下理想割线轨迹，设置仿真时长8 s，步长0.1 s。串联机构末端点沿轨迹运动，可得各关节位移、速度和加速度随时间变化曲线[20-22]，如图5 所示。

从图5 中可知，整个设备在空载状态下，RPP串联机构沿理想割线运动，各关节随时间变化均呈平滑曲线，因此在运动过程中存在的振动和柔性冲击的影响较小。

图5 各关节随时间变化运动曲线

2.4 动力学分析

为了检验RPP 串联机构末端点沿理想割线运动时，转动关节的转矩以及两个移动关节的驱动力随时间变化是否有死点等情况，需要对各关节的Lagrange动力学方程进行求解。

首先对各连杆的质心位置进行求解：

连杆1的质心m1的位置为：

对式（3）相对于时间t求导数，可得质心m1的速度为：

连杆2的质心m2的位置为：

对式（5）相对于时间t求导数，可得质心m2的速度为：

连杆3的质心m3的位置为：

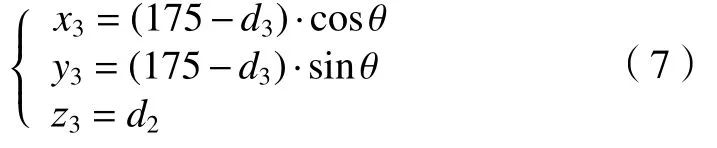
其次对各连杆的速度进行求解，对式（7）相对于时间t求导数，可得质心m3的速度为：

对RPP 串联机构的总动能和总势能以及各连杆的动能和势能求解。质量为m，速度为的质点的动能为。分别求出连杆1、连杆2和连杆3的动能。

RPP 串联机构的总动能为：

质量为m、高度为h的质点的势能为Ep=mgh。分别求出连杆1、连杆2和连杆3的势能。

RPP 串联机构的总势能为：

根据Lagrange 动力学方程

将式（8）～（12）代入式（13）中，可分别计算出关节1的转矩、关节2和关节3的驱动力，其中m1=4.2 kg、m2=4.4 kg、m3=2.8 kg。

式中：m1、m2、m3分别为连杆1、2、3的质量。

由RPP 串联机构各关节运动学仿真分析可知，各关节位置、速度和加速度矩阵。将上述已知条件分别代入式（14）中，可得到各关节随时间变化转矩以及驱动力的曲线，如图6 所示。

图6 各关节随时间变化力曲线

从图6 中可知，整个设备在空载状态下，转动关节、上下运动关节和向心运动关节分别对应的转矩和驱动力随时间变化没有明显的跳变点，且各关节对应的驱动力与转矩数值随时间呈现规律性变化[23]。

2.5 仿真实验

新型固定式割胶机在切割时，胶刀会受到3 个方向的作用力如图7 所示，分别为F1=100 N、F2=100 N、F3=100 N。

图7 作用力示意图

由于丝杠传动模块和传动齿轮组的动力均来自于电机的输出转矩，因此传动齿轮组电机驱动函数表示为STEP(time,5,0d,13,90d);丝杠传动模块5 电机驱动函数表示为STEP(time,5,0d,13,32d)；丝杠传动模块3 电机驱动函数表示为STEP(time,0,0d,5,STEP(time,5,5d,6,STEP(time,6,-0.5d,7,STEP(time,7,0.25d,8,STEP(time,8,-0.5d,9,STEP(time,9,0.75d,10,STEP(time,10,0.25d,11,STEP(time,11,0.25d,12,-0.5d))))))))。由此可得如图8 所示的曲线图。

图8 各关节加速度曲线图

由图8 可以看出，0～5 s 向心运动关节先带动胶刀移动到树皮表面，5～13 s 各关节联动完成割胶工作。整个设备在负载情况下，转动关节和上下移动关节均为单向运动，其加速度曲线呈正弦函数变化。由于树皮表面粗糙，向心运动关节需要快速频发往复运动，其加速度曲线呈无规律变化。综上所述，基于RPP 串联机构的固定式割胶机在切割运动中具有良好的稳定性。

3 结语

（1）基于仿生学设计了一种新型固定式割胶机。将人工割胶过程分解为3 个运动，通过齿轮以及丝杠传动叠加实现割线轨迹，并通过胶刀实现沿割线轨迹切割树皮。

（2）采用机器人理论对割胶机进行理论模型的构建，并以此为基础进行运动学以及动力学求解，为新型固定式割胶机的运动控制提供理论依据。

（3）基于RPP 串联机构的固定式割胶机虚拟样机在模拟负载条件下，加速度无明显跳变，因此具有较好的平顺性，对实物研发提供正向参考价值。