变量相关性对隧道二次衬砌可靠指标的影响

赵东平，吴 楠，涂怀宇

（1. 西南交通大学交通隧道工程教育部重点实验室，四川成都 610031；2. 西南交通大学土木工程学院，四川成都 610031）

长期以来，我国铁路隧道结构设计主要采用安全系数法，这种方法与国际上普遍采用的极限状态法存在较大差异。为与国际标准接轨，自2011年以来，诸多学者在铁路隧道极限状态设计方法领域展开了系统研究，部分成果已经纳入相关规范。赵东平等［1］采用校准法对不同时速的隧道衬砌结构可靠指标开展了研究，提出我国铁路隧道衬砌承载能力极限状态的目标可靠指标建议值；宋玉香等［2］运用Monte Carlo 随机有限元法对复合式衬砌进行了计算研究，提出抽样次数的建议值，得出随机变量的分布特征和各参数的敏感性特征；李奎等［3］对素混凝土衬砌可靠度计算模型的研究表明，作用效应和结构抗力的概率分布类型直接影响衬砌可靠度指标计算方法和计算结果的合理性；谭忠盛等［4］通过对各种结构可靠度算法的比较分析，提出了一种简便实用的二次二阶矩法进行隧道衬砌结构可靠度分析，与改进蒙特卡罗法的对比结果表明，其提出的新方法具有较高的精度；宋玉香等［5］对比分析了响应面法计算结果和Monte Carlo法抽样10 万次计算结果，发现两者具有较高的一致性，验证了响应面法可应用于隧道衬砌的可靠性分析；余永康等［6］采用假定隧道衬砌结构随机变量相关性系数的方法，分析了变量相关性对结构作用效应的影响，结果表明随机变量之间的相关性会对隧道结构的效应产生较大的影响；李晓军等［7］采用数据表（Spreadsheet）法与Monte Carlo 法对盾构衬砌的2 种极限状态进行可靠度分析，结果表明两者误差不超过4%，但Spreadsheet法可节省大量计算时间；苏永华等［8-11］通过理论研究和公式推导，提出了多种隧道结构可靠度指标分析方法，并将这些方法的计算结果与蒙特卡罗法的精确解进行对比，验证了所提方法具有较高准确性；Guo等［12］对隧道支护衬砌进行了可靠性分析，结果表明土体空间变异性对隧道衬砌可靠度有显著影响；Hamrouni 等［13］、Lü 等［14-15］采用响应面法和二阶可靠度计算方法对隧道随机变量的相关性和分布形态开展研究，结果表明考虑摩擦角和黏聚力的相关性会对计算结果产生显著影响。

分析上述成果可知，既有研究聚焦于隧道衬砌随机变量的统计特征、隧道衬砌参数敏感性及土体变量相关性等方面，且研究过程中未考虑衬砌结构设计表达式中随机变量的相关性问题。根据可靠度相关计算理论可知，基本随机变量的相关性与结构功能函数的失效概率相关，即随机变量的相关性与可靠指标有关。

本文依托京张高铁新八达岭隧道工程，采用Monte Carlo 随机有限元方法对隧道衬砌结构设计中的随机变量进行抽样计算，通过确定各个随机变量的相关性系数求解考虑随机变量相关性的隧道衬砌可靠指标，并论证随机变量相关性对隧道衬砌结构截面可靠指标的影响。

1 设计变量相关性

隧道衬砌是偏心受压构件，根据围岩级别和埋深不同，可采用素混凝土或钢筋混凝土衬砌。为了分析隧道衬砌结构设计中随机变量的相关性，首先要建立素混凝土衬砌和钢筋混凝土衬砌的极限状态方程。

1.1 极限状态方程

根据截面受力状态不同，素混凝土衬砌可分为受压和受拉2 种控制状态。2 种状态下对应的衬砌结构极限状态方程［16］分别为

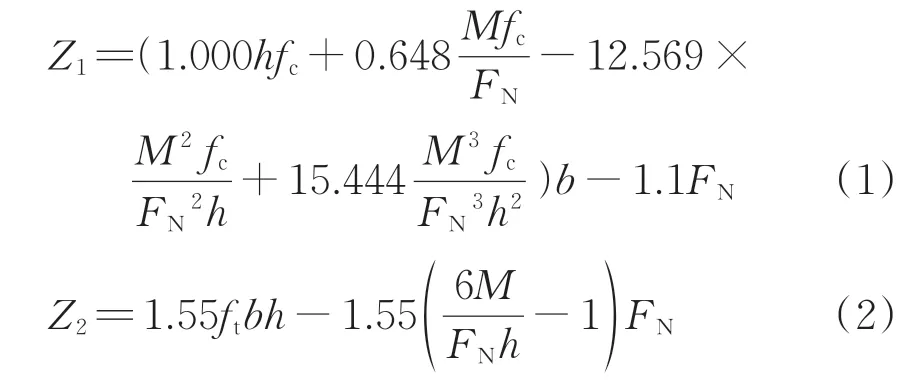
式中：Z1和Z2分别为素混凝土衬砌受压和受拉控制时的极限状态功能函数；h为衬砌截面高度；fc为混凝土轴心抗压强度设计值；M为衬砌截面所受弯矩；FN为衬砌截面所受轴力；b为衬砌截面宽度；ft为混凝土轴心抗拉强度设计值。

根据受压区高度不同，钢筋混凝土衬砌可分为大偏心受压和小偏心受压2 种受力状态。2 种状态下的衬砌结构极限状态方程均为

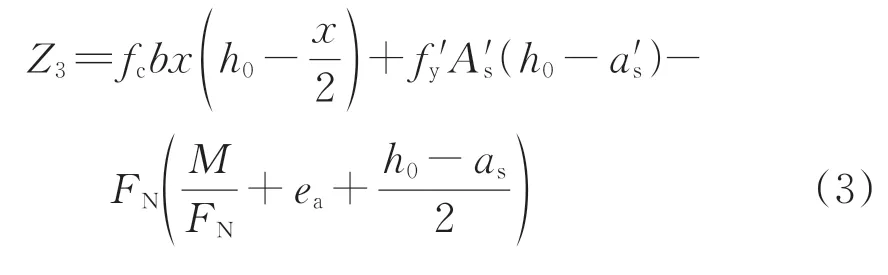
式中：Z3为钢筋混凝土衬砌受力时的极限状态功能函数；x为混凝土受压区高度；h0为衬砌截面有效高度；f'y为钢筋抗压强度设计值；A's为受压区纵向钢筋截面面积；a's为受压区纵向钢筋合力点至衬砌截面受压边缘的距离；ea为附加偏心距；as为受拉区钢筋合力点至衬砌截面近边的距离。

1.2 变量相关性系数

由式（1）—式（3）可知，隧道衬砌结构极限状态方程中涉及多个随机变量，如果这些随机变量之间存在相关性，则可能会对衬砌截面失效概率产生影响。为了确定上述变量之间的相关性，首先要确定式（1）—式（3）中任意2 个随机变量之间的相关性系数。

根据概率理论可知，任意2个随机变量X1，X2之间是否具有相关性以及相关程度大小可通过相关系数ρX1X2来评价，ρX1X2可表示为［17］

式中：σX1，σX2分别为变量X1，X2的标准差；Cov(X1，X2)为变量X1，X2的协方差；μX1，μX2分别为变量X1，X2的均值。

当统计计算得出ρX1X2=0 时，说明2 个变量不存在相关性；当0 ＜|ρX1X2|＜1 时，说明2 个变量之间存在相关性；当|ρX1X2|=1 时，说明2 个变量之间存在强相关性。

式（4）仅能表示2 个随机变量之间的相关性，在式（1）—式（3）的极限方程中涉及多个变量，为便于计算，可将任意2 个变量之间的相关性系数组合为相关性系数矩阵。

对于素混凝土衬砌结构，截面受压和受拉控制状态的相关系数矩阵RSc和RSt分别为

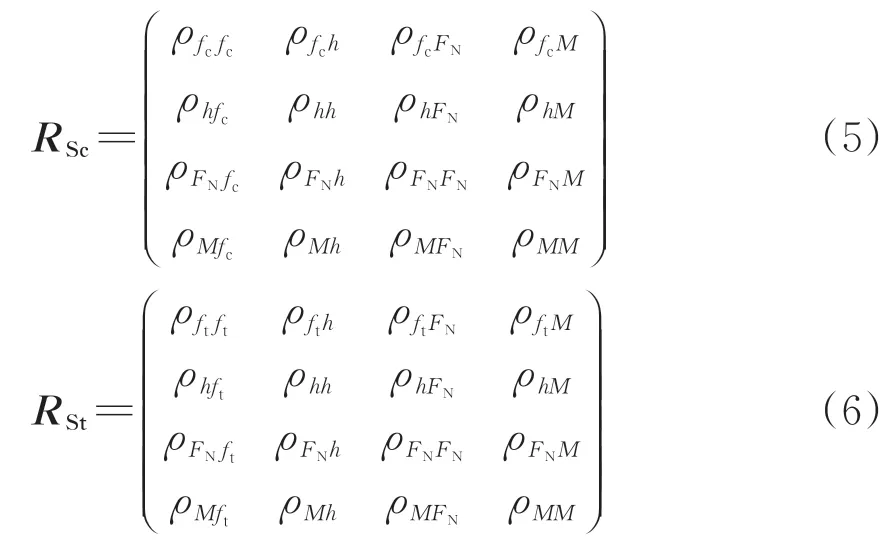
对于钢筋混凝土衬砌结构，其相关系数矩阵RG为

在式（5）—式（7）中相关性系数矩阵参量的下标表示该系数参量对应的2个变量。

1.3 变量相关性对可靠指标的影响

以二维连续分布随机变量为例，当变量存在相关性时，其联合概率密度函数f(X1，X2)［18］为

其中，

对于一般结构而言，功能函数可简化为抗力R与效应S的函数，即功能函数Z=R-S。假设R和S均为正态分布，且R和S的联合概率密度函数为f(R，S)，则功能函数的失效概率Pf为

当随机变量R和S相互独立时，即ρRS=0，联合概率密度函数f(R，S)为

当随机变量R和S具有相关性时，即|ρRS|≤1且ρRS≠0，联合概率密度函数f(R，S)为

其中，

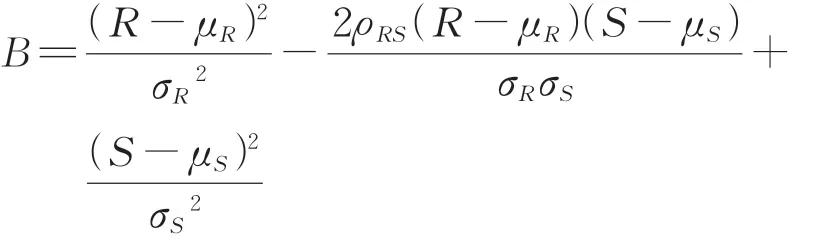
由式（8）—式（11）可知，当随机变量R和S相关时，其联合概率密度函数f(R，S)的表达式不同，功能函数的失效概率也不同，因此随机变量的相关性会影响结构失效概率，进而影响结构可靠指标的计算结果。

目前，用于求解可靠指标的方法主要有验算点法、响应面法及数据表法等。当考虑变量相关性时，数据表法［19-21］相对简便，且形象直观。根据该方法的计算公式，通过Excel 编程可实现考虑相关性的可靠指标计算。

根据数据表法，可靠指标β可由随机变量矩阵、随机变量均值矩阵及协方差矩阵之间通用矩阵运算后求得，其计算表达式为

式中：x为多元正态分布随机变量矩阵，当x为其他分布时，可通过当量正转换为正态分布后再进行计算；F为失效域；μ为随机变量均值矩阵；C为变量协方差矩阵，可由式（13）表示，协方差矩阵中的元素可采用式（5）—式（7）确定的相关系数根据式（4）计算获得。

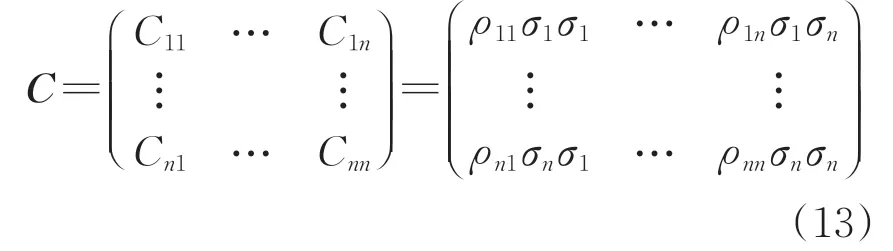
在随机变量空间内，可靠指标的物理含义由式（14）解释，该式表示空间的1个椭球。

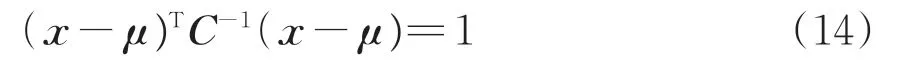
随机变量为二维时，式（14）表示平面内的1个椭圆，椭圆中心在变量均值处；当相关系数ρ=0 时，椭圆的长、短轴分别为σ1和σ2；随着相关系数的变化，椭圆形状也相应改变。椭圆与相关系数的关系如图1所示。

图1 椭圆与相关系数关系

根据上述原理，当标准差变化β倍后，可得到椭圆与极限状态面相切时的方程式为

式中：C*为标准差改变β倍后对应的协方差矩阵。

由于此时椭圆与极限状态面相切，故所求得的β值即为要求的可靠指标，如图2所示。

图2 数据表法可靠指标的确定

2 可靠指标求解

在计算衬砌可靠指标时，首先要确定极限状态方程中随机变量之间的相关性，为此需要进行统计抽样。运用开发的TRAS V1.0 程序，采用Monte Carlo 随机有限元分析与数据表法相结合的方法计算考虑随机变量相关性的衬砌结构可靠指标值。新八达岭隧道工程中的Ⅳ，Ⅴ级围岩深埋地段分别采用素混凝土和钢筋混凝土衬砌，以下分别展示隧道衬砌可靠指标的求解过程。

2.1 计算模型

新八达岭隧道Ⅳ，Ⅴ级围岩深埋衬砌结构尺寸如图3所示。

根据图3所示的结构几何尺寸基于荷载-结构法建立有限元数值模型，采用二维梁单元模拟衬砌，二维杆单元模拟围岩对衬砌的约束作用，模型划分为38个单元，如图4所示。

图3 Ⅳ级围岩深埋衬砌（单位：cm）

图4 衬砌结构可靠性计算模型

2.2 素混凝土衬砌

隧道衬砌结构可靠度计算的难点在于衬砌是多次超静定结构，衬砌截面内力无显式表达式，因此要采用随机有限元抽样计算的方法获取内力的样本数据。

Ⅳ级围岩衬砌采用C30素混凝土，二次衬砌承受荷载比例取50%，此前关于结构材料、围岩弹性反力系数及侧压力系数等基本随机变量的统计特征值已有较全面的研究，本文根据前期研究成果确定了围岩重度、弹性模量、侧压力系数、混凝土轴心抗拉强度、衬砌厚度及弹性反力系数等统计特征［22］，具体见表1。

表1 Ⅳ级围岩深埋隧道衬砌基本随机变量统计特征

经验表明，采用Monte Carlo 随机有限元法进行随机抽样时，若样本容量有限，会对计算结果产生较大影响。为确定抽样次数，使衬砌结构内力统计特征计算结果不受抽样次数的影响，以衬砌拱顶20 号单元为例进行试算，得到轴力和弯矩值样本历史曲线，如图5和图6所示。

由图5和图6可知：拱顶截面轴力及弯矩的均值和标准差变化曲线在抽样5 000次时仍有较大变化，抽样7 500次时趋于平缓，抽样1万次时趋于稳定。

图5 20号单元轴力样本曲线

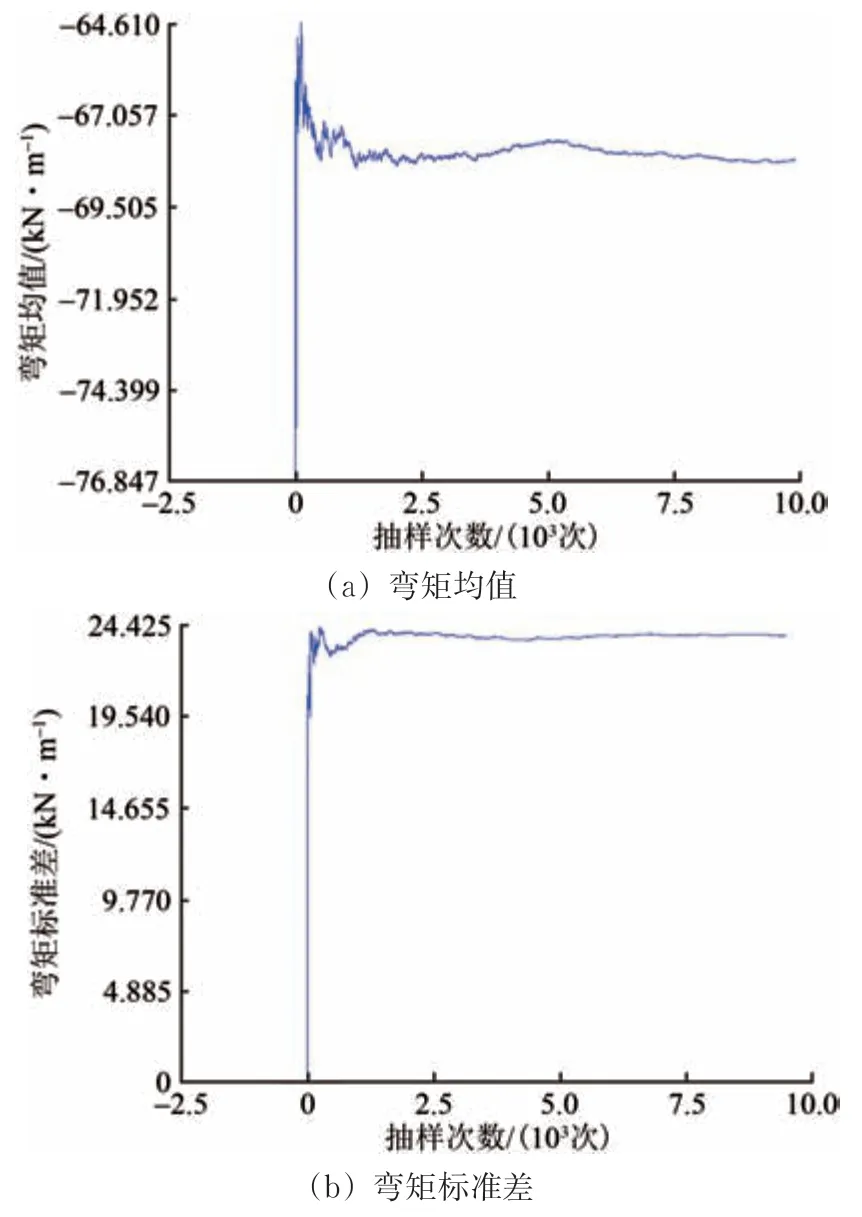
图6 20号单元弯矩样本曲线

衬砌其余截面内力抽样数据的统计特征与拱顶20号截面相似，出于保守考虑确定抽样为1万次进行计算。

对衬砌1 个横断面上的38 个单元分别抽样1 万次，即获得了1 个全截面的抽样数据，通过式（4）计算可得到两两变量之间的相关系数。仍以衬砌拱顶20 号单元为例，计算得到随机变量的相关系数矩阵为

由式（16）可知，除弯矩与轴力之间的相关系数接近于1、具有较强相关性外，其他变量之间的相关系数几近于0，相关性并不明显，故主要考虑弯矩与轴力之间的相关性对计算结果的影响。

对抽样数据进行分析计算，得到该截面衬砌结构内力的统计特征见表2。

表2 衬砌结构内力统计特征

以式（16）和表2中数据为已知参数，根据式（13）计算可得20号单元的协方差矩阵为

根据上述算法，衬砌每一个单元均可计算得出1 个协方差矩阵。根据数据表法，在Excel 中编制相关计算公式，即可求解考虑变量相关性的衬砌各个截面可靠指标。

在Excel 中输入各随机变量的均值、标准差、相关系数矩阵，通过计算得到协方差矩阵和协方差逆矩阵，并编写极限状态功能函数，通过Excel 的规划求解功能计算可靠指标。具体方法为：在“规划求解参数”中，将“设置目标”设置为可靠指标单元格，设置目标为“最小值”；将“可变单元格”设置为试算值单元格，约束条件设置功能函数值小于或等于0；选择迭代求解方法为“非线性”；点击求解后，“可靠指标”单元格即输出求得的可靠指标。

对每一个单元，分别按上述流程进行计算求解，即可得到Ⅳ围岩素混凝土衬砌考虑变量相关性的全截面可靠指标，将可靠指标计算值及差异值、截面偏心距及其抗裂、抗压控制标准0.2h等参数编制于1 张图上，如图7所示。

图7 素混凝土衬砌可靠指标计算结果

为更为直观地将截面可靠指标与衬砌横断面的位置关系对应起来，将每个截面考虑可靠相关性与不考虑相关性时计算得到的可靠指标绘制于衬砌截面上，如图8所示。图中：“＋”表示轴力与弯矩变量之间呈现正相关性。

图8 素混凝土衬砌可靠指标包络图

由图7和图8可知：15，20 及25 号3 个衬砌单元截面偏心距均大于0.2h，属于抗裂极限状态控制；其余断面偏心距均小于0.2h，属于抗压极限状态控制；素混凝土衬砌各单元轴力与弯矩均呈现正相关性；对于抗压极限状态，考虑随机变量相关性与不考虑随机变量相关性的可靠指标计算值，除在仰拱截面和左墙角截面差异值达到6.8%和9.6%外，其余各单元两者差异均小于4%，平均差异为1.2%，即两者的可靠指标结果基本一致；对于素混凝土衬砌抗裂极限状态，考虑随机变量相关性与不考虑随机变量相关性的可靠指标计算值，两者差异在拱顶截面达到最大为67.0%，在左、右拱腰截面差异值分别为56.0%和48.3%，其余各单元两者差异均小于7%，平均差异为30.3%，即两者的可靠指标计算结果差异较大。

2.3 钢筋混凝土衬砌

V 级围岩衬砌采用C35 钢筋混凝土，结构材料、围岩弹性反力系数及侧压力系数等基本随机变量的统计特征值具体见表3。

表3 V级围岩深埋隧道衬砌基本随机变量统计特征

采用与素混凝土衬砌相同的计算方法，计算得到钢筋混凝土衬砌各单元的可靠指标如图9和图10所示。图9中：可靠指标值的正负分别表示轴力FN与弯矩M之间相关性的正负；ξbh0为界限受压区高度，其中ξb为相对界限受压区高度。图10中：“＋”、“－”分别表示轴力与弯矩变量之间相关性的正负。

图10 钢筋混凝土衬砌可靠指标包络图

由图9可知：14，19，20，21及26号5个衬砌单元截面受压区高度小于界限受压高度ξbh0，属于大偏心受压状态，其余衬砌单元均属于小偏心受压状态。

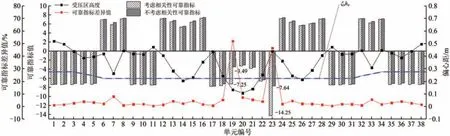
图9 钢筋混凝土衬砌可靠指标计算结果

由图10 可知：钢筋混凝土衬砌各单元轴力与弯矩在仰拱、边墙及拱顶截面呈现负相关性，在拱腰及拱脚截面呈现正相关性；对于钢筋混凝土衬砌小偏心受压截面，考虑随机变量相关性与不考虑随机变量相关性的可靠指标计算值，除在右拱腰截面两者差异值为46.4%（23 号单元）外，其余各单元两者差异均小于8%，平均差异为3.9%，即两者的可靠指标结果基本一致；对于钢筋混凝土衬砌大偏心受压截面，考虑随机变量相关性与不考虑随机变量相关性的可靠指标计算值，两者差异在拱顶截面达到最大为51.9%（19 号单元），其余各单元两者差异均小于8%，平均差异为21.6%，即两者的可靠指标计算结果差异较大。

总体而言，当轴力与弯矩负相关时，考虑变量相关性的计算可靠指标偏大；当轴力与弯矩正相关时，考虑变量相关性的计算可靠指标偏小。

3 结 论

（1）基于2 个综合随机变量概率密度函数的表达式，推导出考虑变量相关性时联合概率密度函数的表达式，论证了考虑变量相关性与否会对失效概率的计算结果产生影响。

（2）铁路隧道衬砌的随机变量中，轴力与弯矩之间相关性较强，对可靠指标的计算结果影响较为显著。当变量之间呈现正相关性时，考虑随机变量相关性的可靠指标计算结果偏小；当变量之间呈现负相关性时，考虑随机变量相关性的可靠指标计算结果偏大。

（3）对于素混凝土衬砌，结构各单元轴力与弯矩均呈现正相关性。随机变量相关性对结构抗压控制状态截面的可靠指标影响较小；对抗裂控制状态截面的可靠指标影响较大，在拱顶截面考虑相关性后的可靠指标值比不考虑时减小67.0%。

（4）对于钢筋混凝土衬砌，结构各单元轴力与弯矩在仰拱、边墙及拱顶截面呈现负相关性，在拱腰和拱脚截面呈现正相关性。随机变量相关性对结构小偏心受压控制状态截面的可靠指标影响较小，仅在右拱腰截面考虑相关性后的可靠指标值比不考虑时增大46.4%；随机变量相关性对大偏心受压控制状态截面的可靠指标影响较大，拱顶截面考虑相关性后的可靠指标值比不考虑时增大51.9%。

（5）采用极限状态法设计铁路隧道衬砌时，宜考虑变量相关性对结构可靠性的影响。对于素混凝土衬砌，可适当提高混凝土强度或增加衬砌厚度，从而保证结构可靠性；对于钢筋混凝土衬砌，可适当减少配筋量以合理利用结构承载能力，从而控制建造成本。