考虑退化相关的装备多部件系统维修决策优化模型
马维宁, 胡起伟,*, 杨志远
(1. 陆军工程大学石家庄校区装备指挥与管理系, 河北 石家庄 050003;2. 国防大学联合作战学院, 河北 石家庄 050003)
0 引 言
近年来,随着大批高新装备的研制并投入使用,部队装备体系发生了巨大变化,对装备维修保障也提出了新的要求。高新装备技术密集、结构复杂,往往是由多型号单体装备组成的复杂系统,承担着多样化、复杂化的军事任务,动用使用频繁,任务时间要求短,保障难度大,维修费用日趋昂贵,对先进维修理论的依赖作用越来越突出。目前维修领域对单部件系统研究相对较多,而对军事装备系统等大部分多部件组成的复杂系统研究相对较少。复杂系统的各组成部件间存在各种关联关系,在这种情况下,单个部件的维修决策优化结果不能直接作为整个系统的维修决策优化结果,否则将影响整个系统维修决策的科学性和合理性。因此,针对装备多部件系统,为确保维修更加高效,系统运行更加安全可靠,考虑部件自身特点和部件间依赖关系的动态维修决策优化研究具有重要意义。
多部件系统的部件间可能存在经济相关、结构相关和随机相关。经济相关包括经济正相关和经济负相关,如果成组维修部件的费用低于部件单独维修的费用,则为经济正相关;如果成组维修部件的费用高于部件单独维修的费用,则为经济负相关。结构相关是指当对某故障部件进行修理时必须要拆卸其他正常工作的部件。随机相关是指部件间的故障或退化将影响其他部件的退化或寿命分布。在多部件系统维修优化问题中,研究较多的是以最小化维修费用为优化目标。如文献[4]利用整数规划方法建立了考虑区间费用的多部件系统预防性维修优化模型,文献[10]在考虑经济相关和失效相关的基础上,建立了多部件系统折扣准则模型,得到了维修费率的最优方程,并采用聚合迭代算法获得了最优解。在部件间随机相关性研究方面,一种研究方法是考虑部件间故障的相关关系。如文献[12]考虑到维修时间有限的约束条件,基于故障率分布建立了考虑预防性维修时间的动态成组维修模型。文献[15]利用Gamma过程描述部件的退化,建立了重型卡车基于役龄的成组更换模型,该模型在决策时刻可以融合系统状态退化信息,更新部件的故障分布,并通过滚动时间窗法不断更新维修决策。随机相关性的另一种研究方法是考虑部件退化的相关关系。如文献[20]建立了考虑退化冲击影响的可靠度模型,并使用蒙特卡罗仿真方法计算了系统可靠度。文献[22]利用回归的方法获得了两部件的交互影响关系式,通过模拟退火算法得到了低温箱的管道视情维修优化结果,证明部件间的交互对于维修决策有着重要影响。
通过分析发现,现有的多部件系统维修优化大多只关注经济相关,而对于随机相关和结构相关考虑较少,忽视了系统中的负载分配以及故障传播导致的随机相关。另外,系统的性能状态是随着使用动态变化的,为此,多部件系统维修决策要能够依据系统状态的变化而动态调整。基于此,本文在Gamma退化过程模型基础上,采用Frank Copula函数考虑分析系统中多部件之间的退化相关性,建立长期运行下系统可用度为目标的维修决策优化模型,采用改进人工蜂群(artificial bee colony,ABC)算法进行求解获得系统最优维修策略,为装备多部件系统维修决策优化提供了新的理论支持。
1 系统描述与退化过程模型
1.1 退化过程模型
令{():∈}表示系统某部件性能退化过程,()表示部件在时刻的性能退化量。若{():∈}满足以下条件:
(1)(0)=0;
(2) 对任意时间0≤<,()-()~Ga((-),),其中Ga(·,·)表示Gamma分布。
(3)()具有独立增量性,即对任意时间0≤<<…<,退化增量()-(),()-(),…,()-(-1)为相互独立的随机变量,此时,称连续时间随机过程{():∈}为Gamma过程,其中>0和>0分别为Gamma分布的形状参数和尺度参数。
对于Gamma过程定义,在任意时间间隔[,]内,系统退化增量()-()服从Gamma分布,其对应的概率密度函数和累积分布函数为

(1)
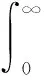
根据定义,Gamma过程为单调非减随机过程。在式(1)基础上,可得系统寿命的分布为
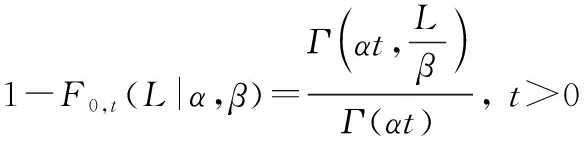
(2)
1.2 系统描述
假设某装备系统由个不同部件串联组成,部件性能指标随工作时间增加不断退化,当退化量超过特定阈值时,部件发生故障。并假设如下:
(1) 每个部件性能退化过程通过一个状态参数即可描述;
(2) 系统各部件退化状态只有通过检测才能得到,且系统各部件的检测是同时进行的,检测结果不存在误差;
(3) 部件故障是软失效,即在发生故障后部件还能继续运行,只是部件性能状态已无法满足使用要求,在初始时刻部件处于全新状态。
为使建立的维修优化模型具有一般性,采用Frank Copula函数描述部件间的交互关系。Copula函数是一种常用的联合分布工具,其提供了丰富的函数族以描述不同的相关性结构,近年来在可靠性领域有一定的应用。元Frank Copula函数可表示为
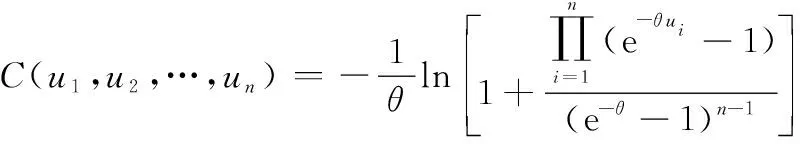
(3)
式中:表示相关性参数,当≥3时,∈(0,+∞),其值越大说明变量间的相关性越强;当→0时,Frank Copula所描述的变量关系趋于相互独立;而当→+∞时,变量间关系趋于完全正相关。
2 装备多部件系统维修决策建模
2.1 维修策略
对系统各部件采取机会维修、预防性维修和故障维修相结合的控制限策略,在运行过程中对各部件退化状态进行检测,第次检测时刻记为,机会维修阈值记为={,…,},预防性维修阈值记为={,,…,},故障维修阈值集合记为={,,…,}。其中,≤≤。部件维修方式包括机会维修、预防性维修和故障维修。
在系统各部件维修结束后,需要根据当前系统部件退化状态确定下次检测时间。为提高检测工作效益,当系统退化量较高时,应当缩短检测时间间隔以防止系统出现故障。假设当前系统各部件退化量为(,,…,),检测间隔期由以下检测规划函数确定:

(4)
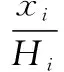
2.2 维修决策优化模型
可用度是衡量装备系统性能好坏的重要指标之一,表示任一时刻系统处于可使用状态的概率。本文以装备多部件系统长期运行情况下可用度最大为优化指标,由以上维修策略可以看出,系统维修决策由变量(,,,)确定。长期运行情况下系统可用度模型表示为
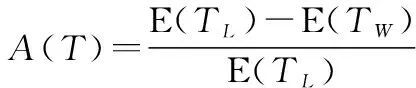
(5)
式中:E()表示系统一个寿命周期内的期望维修停机时间;E()表示系统的期望寿命周期长度。
本文研究完全维修下装备多部件系统的维修决策优化问题。完全维修是指部件经过维修后恢复如新,通常是部件发生故障或有预防性维修需求时,采取更换的方式进行修复,此种方式在装备维修实践中广泛存在。由于系统各部件的维修决策以及后续退化状态只与当前检测时刻的系统状态有关,而与系统历史状态无关,符合Markov特性,由于经过完全维修后的部件又处于全新状态。因此,可将任意维修决策点视为系统退化状态的半更新点,两个连续维修决策点之间的运行时间视为一个半更新周期,在半更新周期内,经过维修后的部件又从全新状态(0状态)开始退化,分析两个连续的维修决策点之间的系统退化特征可近似代替系统的半更新循环过程。在此基础上,分析系统退化状态的稳态特性,进而可以得到系统期望可用度表达式:
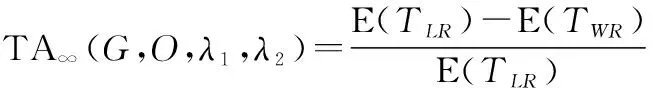
(6)
式中:E()表示一个半更新周期内的维修停机时间;E()表示半更新周期长度的期望值。
2.3 退化状态空间划分
在多部件系统退化建模中,采用连续状态随机过程模型。为建立解析模型,对连续状态退化过程模型进行近似简化,将连续退化过程离散化为有限个状态空间,通过部件在不同退化状态空间的转移近似描述其退化过程。部件的状态空间记为={0,1,…,,…,,},其中,0表示部件完好状态,表示部件故障状态。基于此,部件退化过程可用+2个离散状态进行描述。
部件在时刻的退化量(),其与所属退化状态()之间的关系如下所示:

(7)
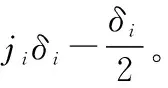
为方便分析,令表示在检测时刻无需采取维修措施对应的系统状态集合,表示在检测时刻有维修活动发生对应的系统状态集合,={(,,…,)|∀,0≤()<},因此,系统状态空间集合可表示为=∪。
2.4 系统退化稳态概率分布
为得到系统状态稳态分布,首先需要计算系统不同退化状态间的转移概率。由以上状态空间划分方法可知,系统退化状态由各部件状态共同决定。因此,首先对单部件状态转移概率进行分析,而后计算系统状态转移概率,在此基础上,可得到系统稳态概率分布。
241 单部件状态转移概率
在检测间隔期[,+1]内,部件状态转移概率与在初始时刻的退化状态和对应的维修方式有关。具体可划分为以下两种情况。
(1) 在检测时刻,如果部件的退化量满足()<,即不需要对其进行维修。根据Gamma过程的独立增量特性,可得部件在时间区间[,+1]内从状态转移到状态(≤≤)的概率为
,(,+1)=((+1)=|()=)=
(lb< Δ< ub)=

(8)
式中:Δ=(+1)-();ub=(-+05);lb=max{0,(--05)}。如果=,即部件在检测间隔期内发生故障,则只需令式(8)中ub=+∞,即可得到对应的状态转移概率。
如果<,容易得到相应的状态转移概率为0,即,(,+1)=0,这是由于部件退化过程是递增的,所以((+1)-()<0)=0。
(2) 在检测时刻,如果系统退化量满足()≥或=,即需要对部件进行维修。在完全维修条件下,部件经过维修后状态恢复如新,此时,部件在时间区间[,+1]内从状态转移到状态的概率可表示为
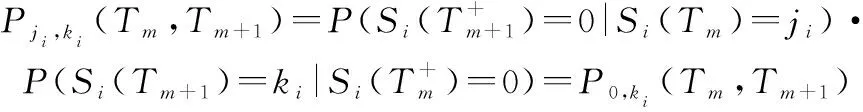
(9)
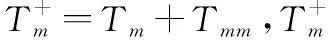
242 系统状态转移概率
在单部件状态转移概率分析基础上,系统在时间区间[,+1]内可能发生的状态转移及相应概率也可分为两种情况,分别如下。
(1) 在检测时刻,若系统状态满足(,,…,)∈,则没有发生维修作业。此时,系统由状态(,,…,)至状态(,,…,),∀,≥的转移概率为
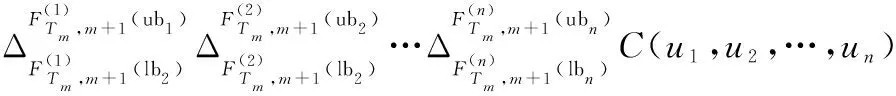
(10)
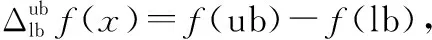
对于系统状态(,,…,),如果满足∃,<,即至少存在一个部件的状态转移情况满足<,显然
(, ,…, ),(,,…,)(,+1)=0,原因与单部件情况相同。
(2) 在检测时刻,若系统状态满足(,,…,)∈,则系统中至少有一个部件需要维修。定义表示在检测时刻采取预防性维修和机会维修的部件集合,表示在检测时刻采取故障维修的部件集合。基于此,在完全维修条件下,系统由状态(,,…,)至状态(,,…,),∀,≥的转移概率可表示为
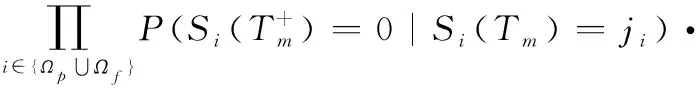
(11)
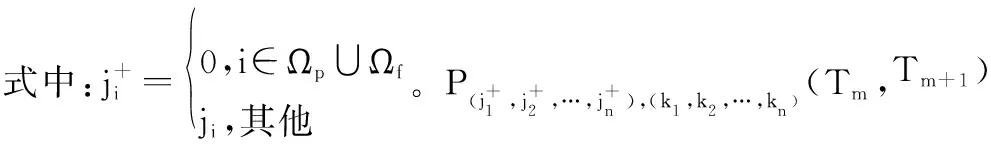
2.4.3 系统状态转移过程及维修方式
系统退化状态Markov转移过程如图1所示。
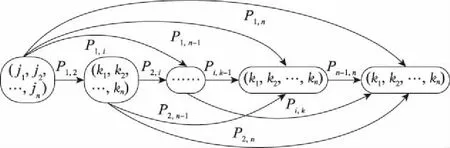
图1 系统退化状态转移过程图Fig.1 Transition process diagram of system degradation state
系统由状态(,,…,)退化至状态(,,…,),若∀,()<,则不采取任何维修方式,只完成系统检查工作;若某部件退化量满足≤()<,则对部件进行预防性维修;若在检测时刻系统有维修活动发生,即∃,有()≥,则对于满足≤()<的所有部件(≠)进行机会维修。否则,不进行机会维修;若某部件退化量满足()≥,则对部件进行故障维修。
244 系统稳态概率分布计算
在以上系统状态转移概率分析基础上,由Markov稳态分布特性可知系统稳态概率分布满足以下方程组:
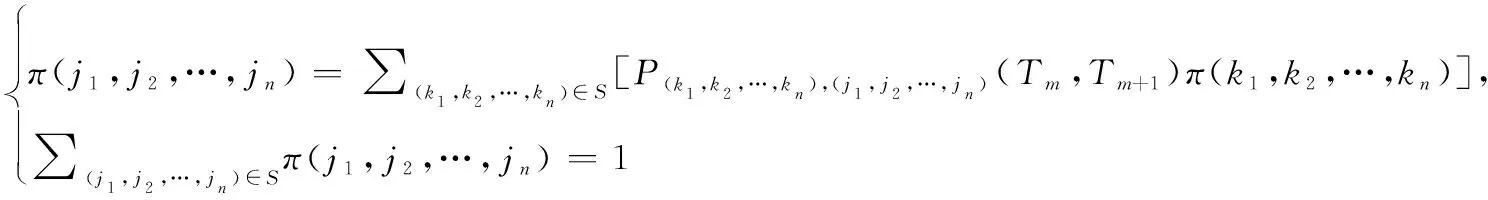
(12)
其中,(,,…,)表示系统处于状态(,,…,)的稳态概率。
2.5 系统期望可用度模型
基于上述系统稳态概率分布,利用系统半更新过程特性,可得到长期运行条件下的系统期望可用度。记系统每次检测时间为,部件的机会维修时间为,,预防性维修时间为,,故障更换时间为,,维修准备时间为,。一般来说,,>,。由于机会维修实质属于预防性维修,因此本文认为机会维修所需时间,与预防性维修所需时间,相等。由式(6)维修决策优化模型可知,要计算系统期望可用度,需分别计算系统维修停机时间和系统半更新周期长度。
(1) 系统维修停机时间
当系统在检测时刻状态为(,,…,)时,令(, ,…, )表示系统在该半更新周期内的期望维修停机时间。
根据(,,…,)取值不同,维修停机时间(, ,…, )可表示为
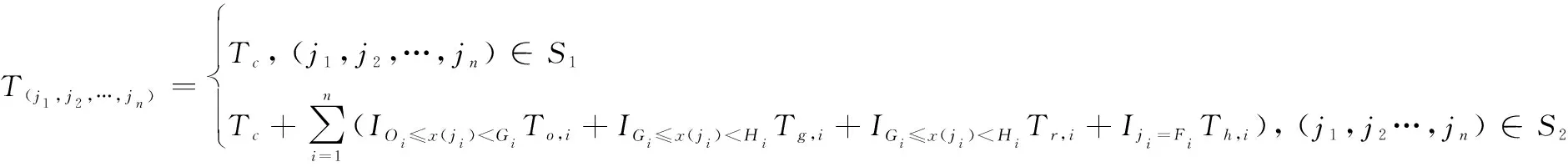
(13)
式中:为示性函数。
结合系统稳态概率分布(,,…,),可得一个半更新周期内系统期望维修停机时间为
E()=∑(, ,…, )∈(, ,…, )π(,,…,)
(14)
(2) 半更新周期长度
半更新周期长度即为检测间隔期,系统检测间隔期由检测时刻的退化状态及相应维修方式决定,令(, ,…, )表示系统当前状态(,,…,)对应的半更新周期长度。根据(,,…,)取值不同,半更新周期长度(, ,…, )取值可分为以下两种情况。
当系统状态(,,…,)∈时,根据检测规划函数式和退化空间划分方法,半更新周期长度可表示为
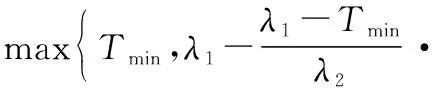
(15)
当系统状态(,,…,)∈时,半更新周期长度可表示为
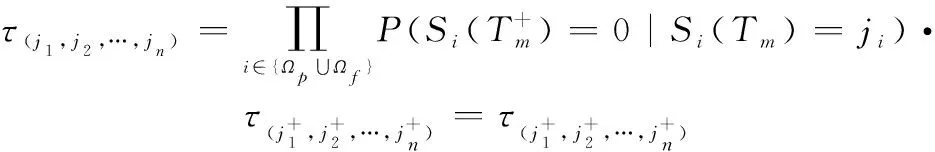
(16)
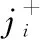
结合系统稳态概率分布(,,…,),可得系统期望半更新周期长度为
E()=∑(, ,…, )∈(, ,…, )(,,…,)
(17)
综合上述系统各状态对应维修停机时间和半更新周期长度,以及系统状态稳态概率分布,在维修决策变量(,,,)确定时,系统期望可用度可表示为
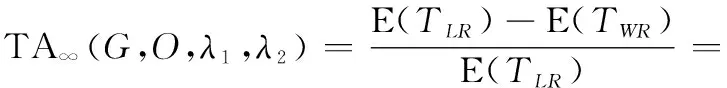
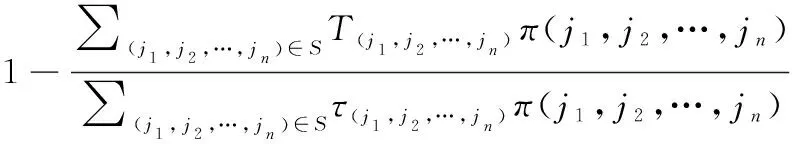
(18)
2.6 维修决策优化模型
在期望可用度模型基础上,以系统期望可用度最大为目标,对维修决策参数(,,,)进行优化。考虑决策变量的约束条件,对应的系统维修决策优化模型如下:
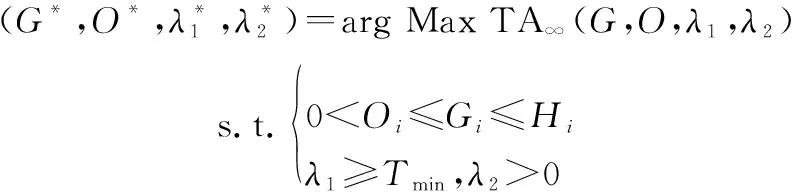
(19)
其中,第一个约束条件限制了机会维修阈值和预防性维修阈值的取值范围。
2.7 基于改进ABC算法的模型求解
上述系统维修决策优化模型中,决策变量对目标函数的影响是非线性、不可微的,且模型决策变化较多,当系统存在个部件时,模型有2+2个决策变量,难以用传统方法得到解析解。当前,智能优化算法已广泛应用于复杂系统维修决策优化,如遗传算法、模拟退火算法、粒子群算法等,虽然这些算法可以得到所建模型的近似最优解,但因为决策变量较多,仍存在全局搜索能力不足、易陷入局部最优等问题。ABC算法是由Karaboga基于蜂群搜索蜜源行为提出的一种启发式群体智能优化算法。相比之下,ABC算法在寻优过程中兼顾局部搜索和全局搜索,控制参数少、易于实现,在非线性函数优化求解方面具有良好的性能。基于此,本文采用ABC算法进行求解。同时,为提高搜索效率,对ABC算法进行改进。对于决策变量和来说,,-2<≤,+2和,-2<≤,+2,与=,和=,对应的系统期望可用度TA是相同的。因此,以将决策变量和的搜索空间转化为,,,∈{0,1,2,…,},,<,,以上处理方法在很大程度上减少了算法搜索空间。
基于以上分析,对于决策变量预防性维修阈值和机会维修阈值来说,采蜜蜂阶段和观察蜂阶段的搜索方程分别为
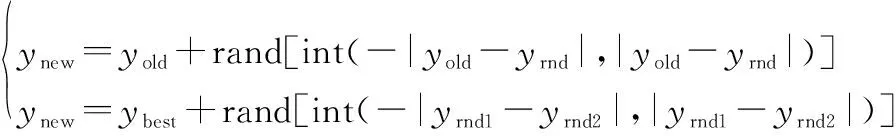
(20)
式中:和分别为蜜源新位置和初始位置;为当前种群最优位置;、和分别为随机选择的其他蜜源位置;rand[int(,)]表示区间[,]内的随机整数;决策变量和,仍采用原来的搜索方程产生备选解。
3 算例分析
该算例考虑某系统由3个存在退化相关的部件组成,为便于分析,假设部件1和部件3相同,每个部件的退化特征均从0状态开始,且服从增量非负、稳定、随机独立的Gamma分布,设定3个部件的故障维修阈值分别为4 mm、5 mm和4 mm,Gamma退化过程的形状参数分别为(,,)=(1,2,1),尺度参数分别为(,,)=(23,12,23),系统检测时间为0.01 h,维修准备时间为0.1 h,状态数量参数均为10,因此,离散状态对应的退化量区间长度(,,)=(04,05,04)。选用Frank Copula函数描述系统中3个部件退化间的相关关系。三元Frank Copula函数可表示为
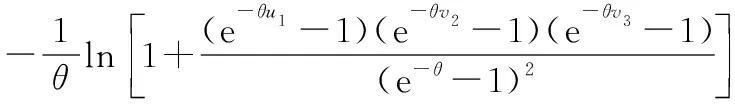
(21)
在本算例中,设定退化相关性参数的值为5。
3.1 系统稳态分布计算
由上述维修决策优化模型知,系统稳态分布与维修决策变量值相关,即在不同的维修决策变量取值(,,,)下,系统稳态分布不同,系统期望可用度也会相应随之变化。以决策变量值(,,,,,,,)=(28,25,28,16,15,16)为例,分析系统稳态概率分布特征,如图2所示。
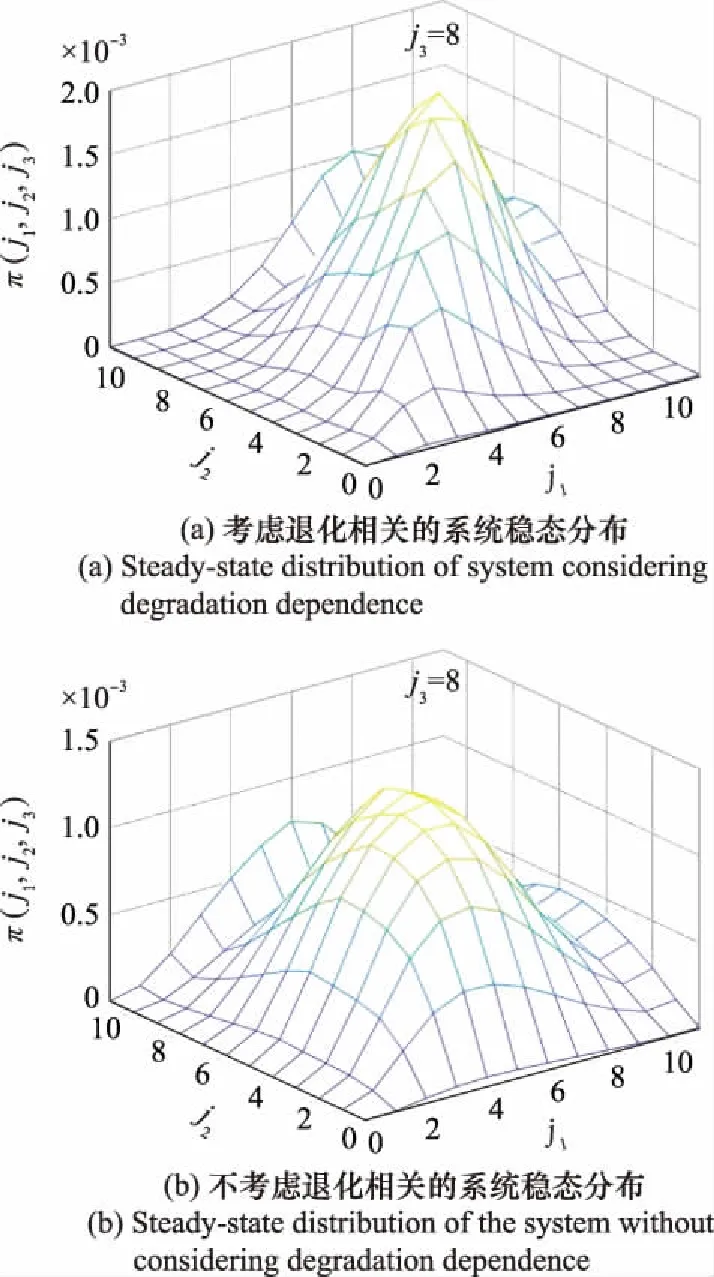
图2 系统稳态分布Fig.2 Steady-state distribution of system
图2分别给出了在部件3状态=8时,考虑退化相关性和独立条件下其余两个部件的稳态分布。由图2对比可以看出,退化相关性对系统稳态分布特征有明显影响,相对于部件相互独立的情况,在系统长期运行条件下,考虑退化相关性时系统退化状态的分布更为集中。同时,由于系统中3个部件不完全相同,且存在一定的相关关系,因此对应稳态分布曲面是非对称的。
3.2 维修策略优化
(1) 检测间隔期参数对优化目标的影响
分析检测间隔期参数(,)变化对系统期望可用度TA的影响。首先,固定预防性维修阈值和机会维修阈值,当预防性维修阈值分别为(,,)=(28,25,28),机会维修阈值分别为(,,)=(2,15,2)时,系统半更新周期内期望可用度随检测间隔期参数(,)的变化趋势如图3所示。其中,的取值范围为[1~5],的取值范围为[02~2]。
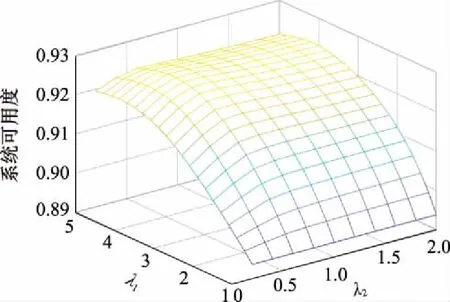
图3 检测间隔期参数对系统可用度的影响Fig.3 Influence of detection interval parameter on system availability
由图3可以看出,当固定预防性维修阈值和机会维修阈值时,随着(,)的增大,TA先增大后减小。这是由于当检测间隔期较小时,频繁的检测会增加维修停机时间,系统运行时间相对减少,因而TA较小。随着(,)的增大,检测间隔期逐渐增大,系统运行时间相应延长,因而TA随之增大。当检测间隔期较大时,会增加系统故障概率,而故障后维修时间一般较长,又会使得TA呈现下降趋势。总体来说,存在最优的(,)值使得TA达到最大。
(2) 预防性维修阈值和机会维修阈值对优化目标的影响
类似地,固定参数(,,)=(04,1,04),(,)=(3,08),分析预防性维修阈值的变化对期望可用度TA的影响,TA随预防性维修阈值的变化趋势如图4(a)所示。之后,固定参数(,,)=(32,4,32),(,)=(3,08)分析机会维修阈值变化对系统期望可用度TA的影响,TA随机会维修阈值的变化趋势如图4(b)所示。

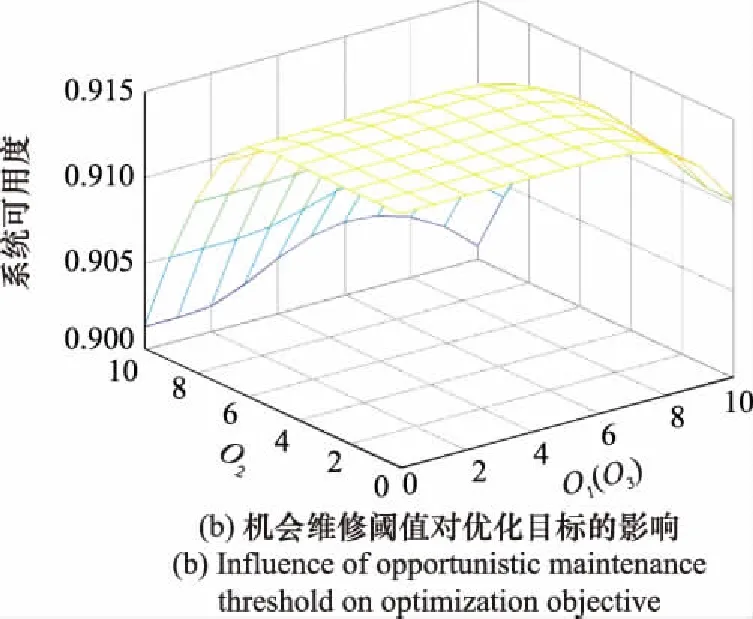
图4 维修阈值对优化目标的影响Fig.4 Influence of maintenance threshold on optimization objective
由图4可以看出,随着预防性维修阈值或机会维修阈值的增大,系统期望可用度TA呈现先增大后减小的趋势。这是因为当或较小时,半更新周期内对各部件预防性维修和机会维修的概率较大,不能充分利用各部件的使用寿命,增加了系统维修停机时间;当或逐渐增大时,预防性维修和机会维修区域缩小,各部件预防性维修和机会维修概率随之降低,TA逐渐增大;当或较大时,系统各部件发生故障的概率较高,受故障后维修时间较长的影响,导致TA相应减小。总体来说,存在最优维修阈值和使得系统期望可用度TA最大。
(3) 基于ABC算法的维修策略优化
设置ABC算法的优化参数为种群数量10,更新次数20,最大迭代次数100,ABC算法的一次优化迭代过程如图5所示。
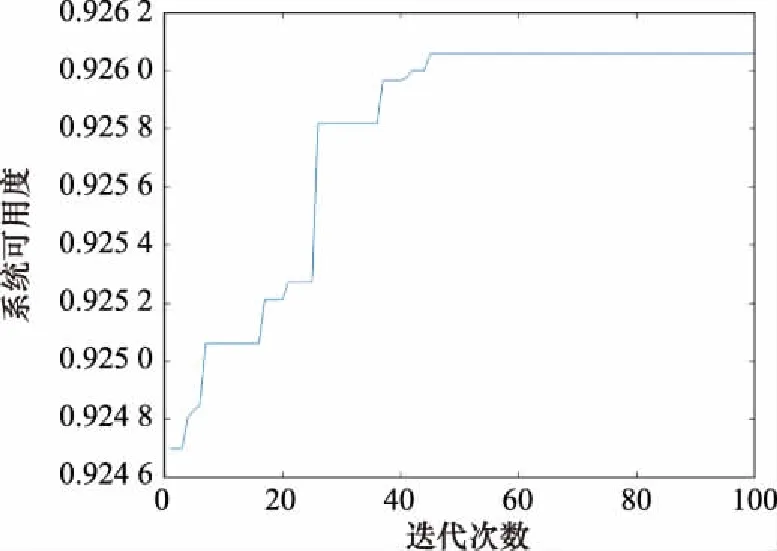
图5 ABC算法的一次优化过程Fig.5 An optimization process of ABC algorithm
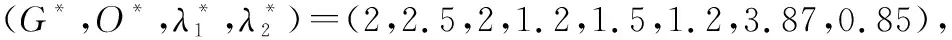
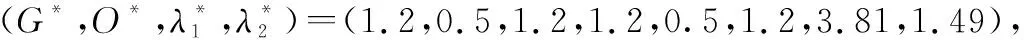

3.3 灵敏度分析
针对本文所建立的维修决策优化模型,影响系统可用度的3个重要因素分别是维修停机时间、Copula函数中退化相关性参数和各部件状态数量参数,在此分析这3个参数对优化结果的影响。
3.3.1 维修准备时间
维修准备时间直接影响系统可用度的大小。在其余参数设置不变的条件下,分析维修停机时间对优化目标的影响,如图1所示。
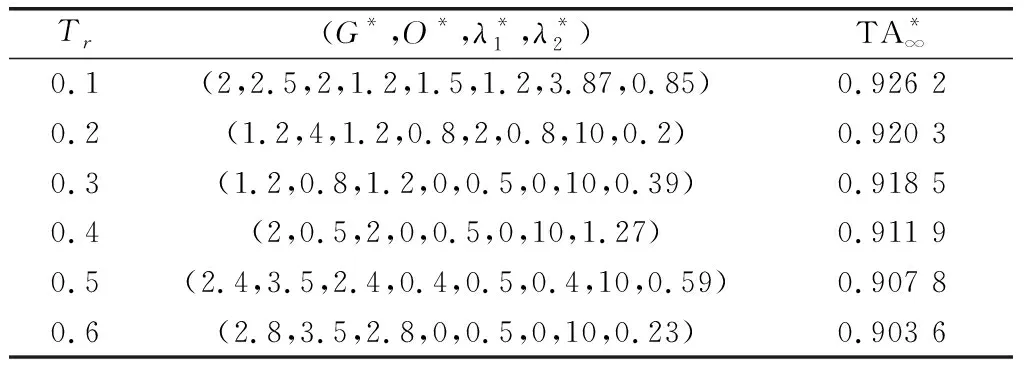
表1 维修准备时间对维修优化结果的影响Table 1 Influence of maintenance preparation time on maintenance optimization result
由表1可知,随着维修准备时间的增大,系统运行时间相应减小,系统可用度呈逐渐下降趋势,特别是当维修准备时间较长时,会出现部件机会维修阈值为0的情况,这表明在检测时刻就要对相应部件进行更换,这也说明利用维修停机时间对尽可能多的部件同时安排维修工作的重要意义。
3.3.2 退化相关性参数
本文考虑退化相关条件下多部件系统的维修决策优化问题,因此需要分析退化相关性参数θ对优化结果的影响。在系统退化过程和其他参数不变的情况下,不同θ值对应的最优维修策略如表2所示。

表2 退化相关性参数对维修优化结果的影响Table 2 Influence of degradation dependence parameter on maintenance optimization result
由表2可知,随着退化相关性参数的增大(即系统部件间退化相关性的增强),系统最优视情维修策略也会相应发生变化。注意到当值较大时(>5),部件维修阈值会相应降低,这是由于为确保系统长期稳定可靠运行,维修阈值的降低可以提前对部件进行预防性维修和机会维修,从而提高了系统可用度。
同时,随着退化相关性参数的增大,系统期望可用度也随之提高,这是由于随着部件间退化相关性的增强,可以利用维修停机时间对相关部件进行同时维修,减少了额外的维修停机时间,从而提高了系统的可用度。
333 状态数量参数
本文在推导系统稳态概率分布时,采用离散化系统状态近似代替连续状态退化过程,各部件状态数量参数会直接影响系统期望可用度的计算精度,因此,有必要分析状态数量参数对优化结果的影响,如表3所示。

表3 状态数量参数对维修优化结果的影响Table 3 Influence of state amount parameter on maintenance optimization result
由表3可知,在不同的状态数量参数下,系统有着不同的最优预防性维修阈值和机会维修阈值。状态数量参数越小,系统可用度越大。随着状态数量参数的增大,系统期望可用度逐渐降低。这是由于状态数量参数的变化,引起系统预防性维修阈值和机会维修阈值的变化,系统维修停机时间逐渐增大,从而导致系统可用度降低。
4 结 论
本文考虑装备多部件系统任务特性的实际需求,以长期运行下系统可用度为目标建立了维修决策优化模型,采用Gamma过程描述系统退化过程,采用Frank Copula函数描述系统各部件间相关关系,并利用改进ABC算法进行了求解,获得了系统最优检测间隔期和维修阈值,通过算例验证了模型的有效性和可实施性,为装备多部件系统预防性维修策略的实施提供了理论支持。

