基于互质阵虚拟阵列空间平滑的相干信号DOA估计方法
韦 娟, 严世安, 宁方立
(1. 西安电子科技大学通信工程学院, 陕西 西安 710071; 2. 西北工业大学机电学院, 陕西 西安 710072)
0 引 言
波达方向(direction of arrival,DOA)估计是一种阵列接收信号获取信号入射方向信息的技术,被广泛应用在雷达、声纳、无线通信等领域。目前多以非相干信号为研究对象,但在实际信号传播过程中,由于多径传播和同频干扰造成大量相干信号源存在,因此相干信号的DOA估计亦是一研究热点。
均匀线阵相干信号DOA估计算法中,以空间平滑、Toeplitz矩阵重构为基础的解相干算法,均存在阵列孔径损失问题。可以通过增加阵元数来提高DOA估计算法的角度自由度(degrees of freedom,DOF),但该方法会增加系统部署成本;亦可引入如互质阵列、嵌套阵列等非均匀稀疏阵列构建虚拟阵列以拓展阵列孔径。互质阵列是由两个阵元数分别为互质数的均匀子阵相互穿插形成,结合了稀疏阵列的优势和质数的性质,能够突破奈奎斯特采样定理的限制,阵列部署灵活,具有广阔的应用前景。
前向空间平滑(forward spatial smoothing,FOSS)算法是最早被提出来估计相干信号DOA的,但该方法孔径损失严重。前后向空间平滑(forward and backward spatial smooth,FBSS)算法利用了后向子阵列,增加了平滑次数,增大了阵列孔径,拥有比FOSS算法更高的DOF,但对信号没有进行完全的解相干。Han等提出了一种类旋转不变子空间信号参数估计(estimating signal parameters via rotational invariance techniques-like,ESPRIT-like)算法,将数据协方差矩阵的任意一行构造成Toeplitz矩阵,能够完全消除信号的相干性,利用ESPRIT-like算法进行DOA估计,但该算法估计精度低,亦存在阵列孔径损失。Stoica等提出的最大似然(maximum likelihood,ML)估计算法以及Ottersten等提出的加权子空间拟合(weighted subspace fitting, WSF)算法均可以在不损失阵列孔径的前提下对相干信号进行DOA估计,但这两种算法包含多维非线性搜索,计算复杂度高,且初值设置对于DOA测向影响较大。Wang等提出的通过四阶累积重构Toeplitz矩阵进行相干信号DOA估计,DOA估计精度较高,但计算复杂度高。Zhang等提出了一种基于多重Toeplitz矩阵重构的DOA估计方法,对相关矩阵的平方进行加权求和,以形成满秩等效数据协方差矩阵。该算法无需提前消噪,但低信噪比、低快拍条件下估计性能不佳。唐晓杰等提出了一种前后向多重Toeplitz矩阵重构(forward and backward multi-Toeplitz,FBMT)算法,构造了 Toeplitz 矩阵,通过误差最小准则构造代价函数,实现相干信号的 DOA 估计。该方法无需信源数先验信息,但阵列孔径损失严重,低信噪比条件下估计性能较差。Peng等提出一种将协方差矩阵子矩阵对角线元素之和的共轭作为加权因子的自加权空间平滑(self-weighted spatial smoothing,SWSS)算法,信号估计精度较高,由于采用空间平滑预处理,依旧存在阵列孔径损失。
基于此,对互质阵虚拟阵列的连续部分进行空域平滑,提出一种基于互质阵列虚拟阵列空间平滑(coprime array virtual array spatial smoothing,CASS)的相干信号DOA估计方法,该算法不需要信源数先验信息,利用互质阵虚拟阵列可以实现DOF拓展的特点,搭载空间平滑算法进行相干信号DOA估计。在低信噪比环境下对于信号的DOA估计精度以及鲁棒性拥有较好表现。
1 阵列信号模型
1.1 互质阵列接收信号模型
互质阵列利用虚拟域信号处理方法,在虚拟域上形成一个增广的虚拟阵列,对该虚拟阵列信号进行与均匀线阵等价的统计信号处理,能够有效提升DOA估计的DOF。
互质阵列结构如图1所示,该阵列由两个均匀线阵嵌套构成。
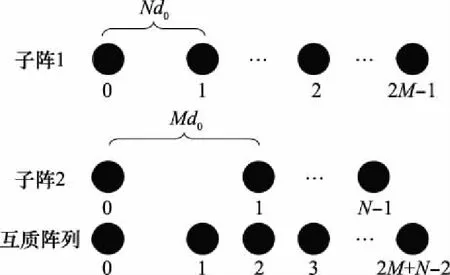
图1 互质阵列Fig.1 Coprime array
其中,,为互质的两个数,虚拟阵元间距=2。互质子阵1为2元均匀线阵,阵元间距为,子阵1阵元位置为{|0≤≤2-1}。互质子阵2为元均匀线阵,阵元间距为,子阵2阵元位置为{|0≤≤-1}。
互质阵列物理阵元真实位置为=[,,…,2+-2]。
互质阵虚拟等效差联合阵列如图2所示。

图2 互质阵列虚拟阵列Fig.2 Virtual array of coprime array
虚拟阵元位置为={ ±(-)|0≤≤2-1, 0≤≤-1}。其中,虚拟阵列阵元位置-(+-1)与(+-1)之间无空洞,可以视为均匀线阵。
个信号入射到互质阵列接收信号为
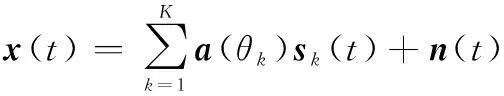
(1)
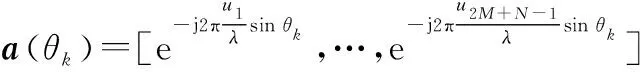
对于第个相干信号可表示为
()=(),=2,3,…,
式中:()为原始参照信号;为相干系数。
1.2 空间前后向平滑处理
互质阵列协方差矩阵为

(2)
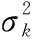
对接收协方差矩阵进行向量化处理:

(3)
式中:=vec (),为单位矩阵;=[()⊗(),…,()⊗()],⊗表示Kronecker内积,(·)表示共轭。
通过在Toeplitz矩阵结构中重新排列的元素可获得虚拟阵列信号的等价协方差。由于信噪比和快拍数对协方差矩阵的影响,同一波程差对应的协方差矩阵元素不同,故对同一波程差对应的元素取平均值:

(4)
式中:(diff)表示同一波程差diff对应的第个协方差矩阵元素;(diff)表示波程差diff相同的协方差元素总和。
在互质虚拟阵列空洞位置插入天线,将联合差阵列变为均匀线阵后,假设空洞处天线无接收信号。根据波程差元素对协方差矩阵进行扩展,构成Toeplitz矩阵∈(2-+1)×(2-+1)。

(5)
式中:1<,<2-+1。
尽管矩阵包含所有互质阵列信号信息,但由于稀疏阵列特性,是低秩矩阵,把看作部分数据信息缺失的协方差矩阵,利用低秩矩阵恢复理论,对矩阵中的零元素进行近似填充。
创建优化问题:
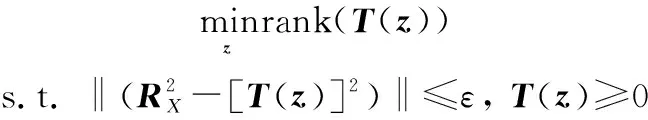
(6)
式中:()是以复向量为第一列的Hermitian Toeplitz矩阵,∈(2-+1)×1;为协方差矩阵拟合误差。
由于矩阵秩函数是非连续、非凸函数,利用迹范数最小化对式(6)进行凸松弛表示:
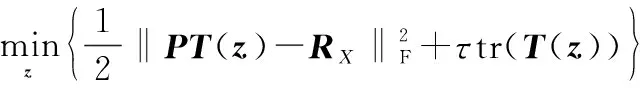
(7)

构建映射矩阵,∈(2-+1)×(2-+1)。
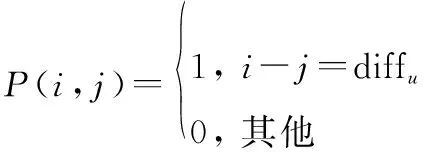
(8)
由于,向量的首元素无法进行共轭拓展,故将第一个元素初值先定义为实数,经CVX工具箱计算得到的整体优化向量后,再对其初值进行优化。
经凸优化重构后的矩阵()可看作由2-+1个阵元组成的均匀阵列的协方差矩阵。为提高算法估计精度,对重构后的Toeplitz矩阵()进行前后向空间平滑分成个子阵列。为避免虚拟阵列内插零阵元造成协方差秩亏损,滑窗长度须不小于连续差联合子阵正向长度(+-1)。滑窗长度设置为=+-1。
FOSS处理如图3所示。

图3 FOSSFig.3 FOSS
前向平滑时,定义第个子阵列接收数据为
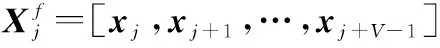
(9)
第个子阵接收数据协方差矩阵可表示为
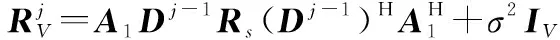
(10)

FOSS后的协方差矩阵可通过各子阵的协方差矩阵求平均而得
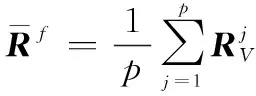
(11)


(12)
式中:为置换矩阵,其反对角线元素均为1,其余位置全为0。
将FOSS矩阵及后向空间平滑矩阵取平均得到FBSS矩阵(∈(+-1)×(+-1));
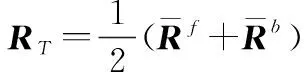
(13)
由于除2以外的质数均为奇数,当=2时,为奇数,则+-1为奇数;当>2时,,均为奇数,则+-1为奇数。即对于互质阵列,子阵阵元数<时,连续位置+-1均为奇数。则构建的Toeplitz矩阵为奇数阶。
Toeplitz矩阵可以看作阵元位置为{-,…,0,…,}均匀线性阵列的输出协方差矩阵:
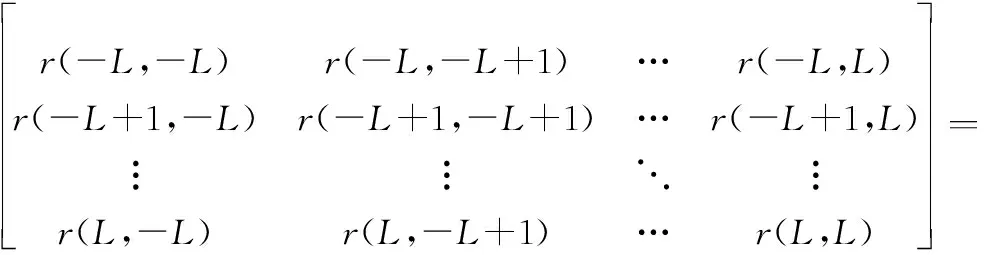
(14)
式中:=(-1)2。
对于相干信号,又有

(15)
式中:
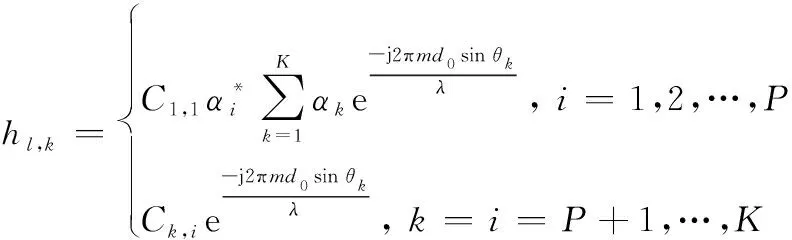
(16)

2 基于后向平滑的相干信号估计
2.1 重构后向平滑Toeplitz矩阵
选取的第行:
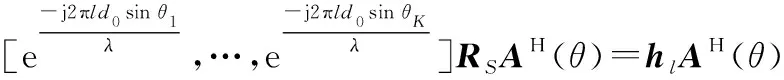
(17)
式中:=[,1,…,,],且信号协方差矩阵中不会存在全零行,因此中不存在零元素。利用长度为+1的滑窗截取的元素,得到行向量:
,=[(,-),(,1-),…,(,-)], 0≤≤
(18)
取第一个行向量,0:

(19)
式中:
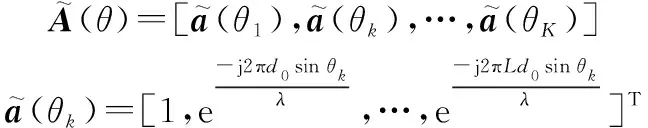
利用向量重构Toeplitz矩阵:
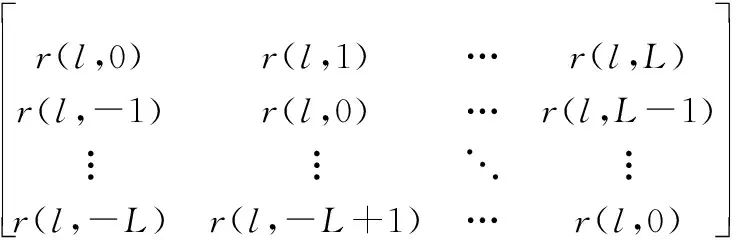
(20)
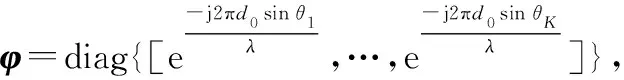
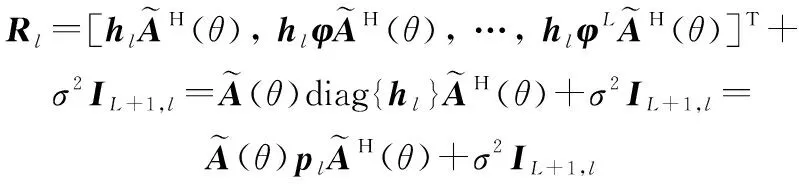
(21)
式中:+1,表示第条对角线元素为1,其余元素均为零的+1阶方阵;=diag{}表示矩阵重构后的虚拟信号协方差矩阵。
忽略噪声影响,可以写为
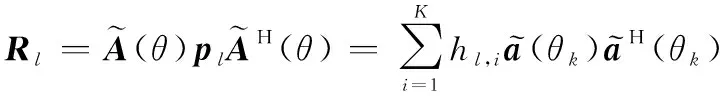
(22)
2.2 凸优化去噪处理
对于第个信号,必存在∈1×(+1)和其余-1个导向矢量张成的信号子空间正交:

(23)
式中:range{·}表示张成的子空间。
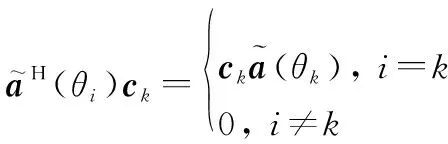
(24)
将式(24)代入式(22)得
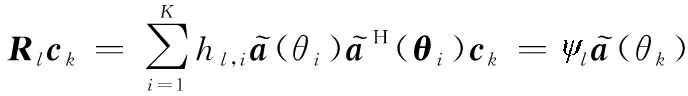
(25)
根据正交性质,有

(26)
考虑到噪声影响,式(26)可表示为
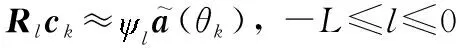
(27)
为减小误差,利用每次平滑的子阵列构造代价函数,得到凸优化模型:
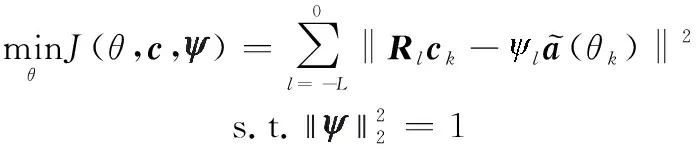
(28)



(29)
构建映射矩阵:
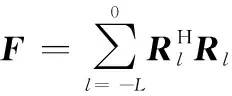
(30)
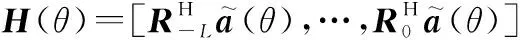
(31)
又
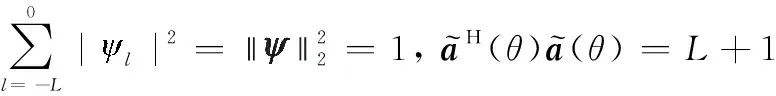


(32)

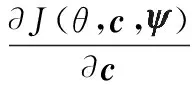
(33)
式(33)的根为

(34)
式中:(·)表示伪逆。
将式(34)代入式(28)得

(35)
将()()进行特征值分解:
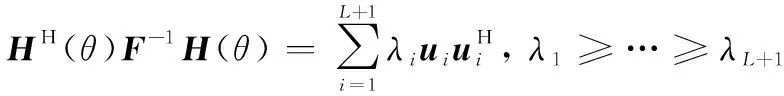
(36)

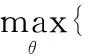
(37)


()=+1-max eig{()()}
(38)
式中:max eig{·}表示特征值分解后最大特征值。
构建谱函数():
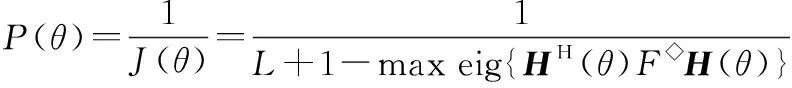
(39)
对()进行谱搜索,对每个()()求其最大特征值,()谱峰对应角度即为DOA估计方向。
算法步骤归纳如下:
根据式(2)计算阵列数据协方差矩阵=E{()()};
根据式(4)对虚拟阵列元素进行整合,根据式(5)构建矩阵;
利用CVX工具箱,根据式(7)重构;
对矩阵进行后向平滑矩阵。用+1长度的滑窗截取,根据式(17)得到;
根据式(30)、式(31)计算映射矩阵和();
根据式(39)计算空间谱函数(),通过谱峰搜索得到信号DOA。
2.3 算法DOF分析
由2+-1个阵元组成的互质阵列经Toeplitz重构产生(),因平滑子阵阵元数目大于等于相干信号数时,可以有效解相干。则对()进行空间平滑时,>。且由于对互质阵虚拟阵列进行了空洞填充处理,为保证信号信息的完整,滑窗长度不小于虚拟连续阵列正向长度(+-1),即≥+-1。则取滑窗长度=+-1,经前后向空间平滑预处理后,生成矩阵∈(2+1)×(2+1),其中=(+-2)2。
矩阵不存在秩亏损,对矩阵第行进行空间平滑处理生成,此时滑窗长度只需不小于信源数即可完成对的解相干。滑窗长度取最小值,即假设噪声子空间仅由一条导向矢量构成,滑窗长度为+1。
综上,2+-1个阵元组成的互质阵列,其虚拟阵经空间平滑后最多可以完成(+)2个相干角度估计。
3 实验分析
本节通过仿真实验将CASS算法与文献[15]提出的FBSS算法、文献[18-20]提出的ML算法、文献[28]提出的FBMT算法、文献[29]提出的SWSS算法进行比较,对不同条件下的均方根误差(root mean square error, RMSE)进行分析。RMSE可以通过500次蒙特卡罗实验得到:
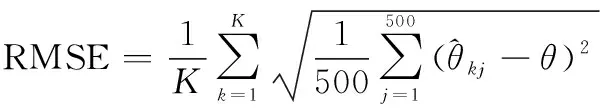
(40)
式中:为信源数。
设信号为零均值高斯信号,噪声为零均值高斯白噪声。由于FBSS算法、ML算法、SWSS算法需要信号源数先验信息,而FBMT算法和CASS算法无需信号源数。故仿真实验中,FBSS算法、ML算法、SWSS算法的信号源数是已知的,FBMT算法和CASS算法信源数先验信息均未知。
为方便DOF的比较,CASS算法构建互质阵列子阵阵元数分别为2=6,=5,总阵元数为10。作为不损失阵列孔径算法对照,ML算法采取10元均匀线阵。由于CASS算法、ML算法可以实现相干信号的最大测向数为9。FBSS算法、FBMT算法、SWSS算法构建的均匀阵列阵元设置为17,即完成9个相干信号DOA估计的FMBT算法所需要的最小阵元数。
3.1 全相干信号的估计性能分析
3.1.1 不同信噪比条件下的算法性能
假设9个入射信号均相干,入射角度分别为[-66°,-42°,-30°,-15°, 0°, 10°, 25°, 42°, 56°]。相干系数分别为=[1, 02ejπ3, ejπ4, 04ejπ6, ejπ5, 06ej2π5, ejπ7, 08ej2π7, ej3π7],正则化参数=1.5×10,快拍数为500,扫描间隔为0.1°。全相干信号中信噪比对算法估计精度的影响如图4所示。分析图4可知, FMBT算法由于已经达到其最大信号测量角度极限,高信噪比条件下测向性能与FBSS算法接近。ML算法由于测向信号较多,难以保证经多次角度代入处理收敛到的局部最小值是真实信号值。SWSS算法由于利用信号协方差信息,在低质量信号中提取出有效信息能力较强,估计精度较高。在信噪比为-12~-4 dB条件下,CASS算法由于对原互质阵列进行同波程差数据整合以及前后向空间平滑,增强了信号强度,估计精度高。CASS算法由于填补虚拟阵列空洞,存在信息缺失,故在8 dB信噪比条件下估计性能略差。

图4 全相干信号信噪比对不同算法估计精度的影响Fig.4 Influence of signal to noise ratio of fully coherent signal on the estimation accuracy of different algorithms
全相干信号-12 dB条件下各算法的归一化功率谱如图5所示。分析图5可知,在低信噪比条件下,FBSS算法由于没有进行完全解相干,估计精度较低;ML算法在对多个相干信号进行DOA估计时,需要选定合适的初值,DOA估计精度受初值设置影响。FBMT算法没有对信号信息进行预处理,噪声影响较大,不能准确估计DOA;SWSS算法在较大噪声干扰下,无法通过加权子空间算法估计准确的DOA。CASS算法经过预处理,去噪相对彻底,算法精度较高。
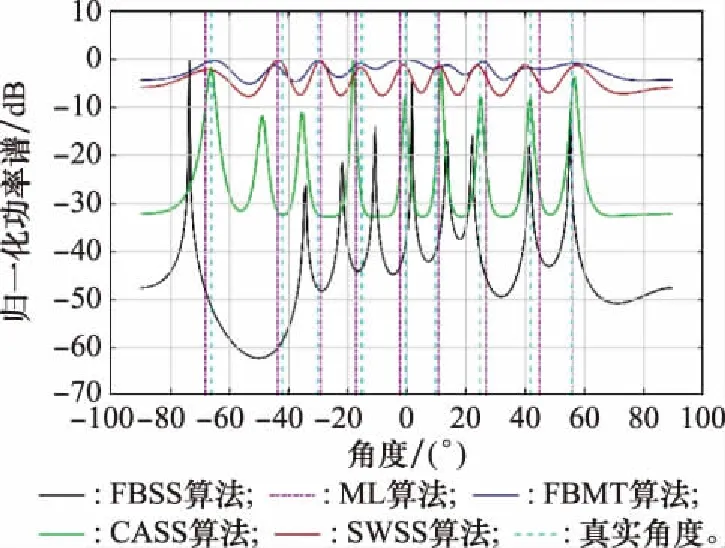
图5 全相干信号-12 dB条件下的归一化功率谱Fig.5 Normalized power spectrum of fully coherent signal at -12 dB
3.1.2 不同快拍数条件下的算法性能
设置信噪比为0 dB,其余仿真环境同第3.1.1节。全相干信号中快拍数对算法估计精度的影响如图6所示。
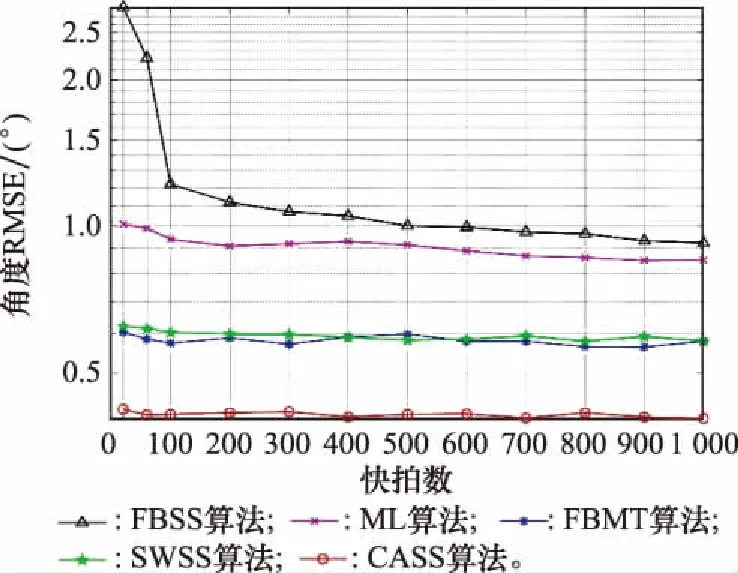
图6 全相干信号快拍数对不同算法估计精度的影响Fig.6 Influence of snapshots number of fully coherent signal on the estimation accuracy of different algorithms
分析图6可知,FBSS算法估计性能受快拍数影响较大,且随着快拍数增加,估计精度提升明显。在快拍数为20时,ML算法、FBMT算法、SWSS算法以及CASS算法估计精度远高于FBSS算法。且CASS算法在快拍数为20时依旧保持良好的算法精度,估计性能最佳。
3.2 部分相干信号的估计性能分析
3.2.1 不同信噪比条件下的算法性能
假设入射角度为[-66°, -42°, -30°, -15°, 0°, 10°, 25°, 42°, 56°]的9个信号,前6个信号为相干信号,后3个信号是与其他信号完全不相干的信号。正则化参数τ=1.5×10,快拍数为500,扫描间隔为0.1°。部分相干信号中信噪比对算法估计精度的影响如图7所示。
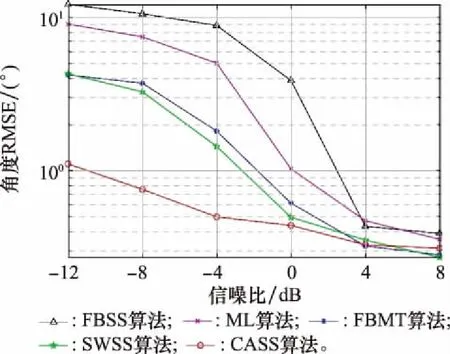
图7 部分相干信号信噪比对不同算法估计精度的影响Fig.7 Influence of signal to noise ratio of partially coherent signal on the estimation accuracy of different algorithms
分析图7可知,对于部分相干信号,FBSS算法在低信噪比条件下估计精度依旧较低。ML算法、FBMT算法与SWSS算法估计精度均低于CASS算法。CASS算法在低信噪比条件下估计角度均方误差较小。
部分相干信号-12 dB条件下各算法的归一化功率谱如图8所示。
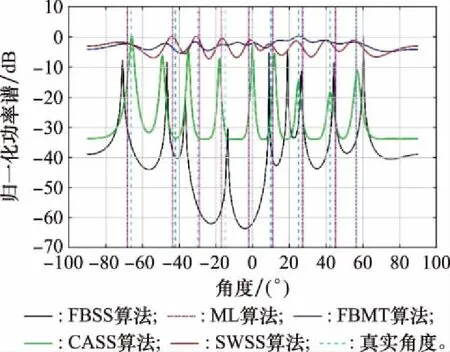
图8 部分相干信号-12 dB条件下的归一化功率谱Fig.8 Normalized power spectrum of partially coherent signal at -12 dB
分析图8可知,在部分相干信号中,FBSS波峰尖锐,完成所有DOA估计,但与真实角度偏差较大。 ML算法经多维非线性搜索,收敛值不能保证为全局最佳。FBMT算法在已达到其相干信源数估计极限的情况下,功率谱函数波峰较平;SWSS算法经自加权处理,在低信噪比条件下能够有效去噪,波峰较尖锐。CASS算法由于凸优化去噪相对彻底,其混合信号估计性能与全相干信号估计性能相对稳定。
3.2.2 不同快拍数条件下的算法性能
设置信噪比为0 dB,其余仿真环境同第3.2.1节。部分相干信号中快拍数对算法估计精度的影响如图9所示。
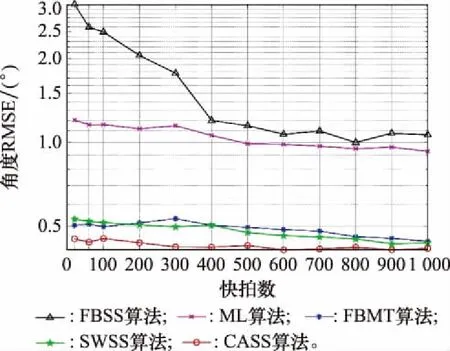
图9 部分相干信号快拍数对算法估计精度的影响Fig.9 Influence of snapshots number of partially coherent signal on the estimation accuracy of algorithm
分析图9可知,FBSS算法估计精度随快拍数增加而提高。ML算法、FBMT算法、SWSS算法、CASS算法随快拍数增加估计精度变化曲线较为平稳。CASS算法估计性能最佳,且在低快拍条件下性能稳定。
3.3 运算时间比较
实验仿真环境为Matlab R2020a平台,Inter i7-9570H处理器,16 G内存。仿真条件同第3.1.2节。各算法运算时间比较如图10所示。

图10 不同算法运算时间比较Fig.10 Comparison of operation time of different algorithms
分析图10可知, FBSS算法只经过空间平滑处理,运算速度最快;ML算法由于需进行多维搜索,且DOA估计数目愈多,运算时间愈长;FBMT算法由于进行多次前后向空间平滑处理及特征分解处理,运算时间也相对较长。SWSS算法由于需要对信号协方差进行加权累加,随着精度要求的提高,迭代次数变多,计算复杂度增高;CASS算法采用互质阵列作为接收阵列,阵元数较少,且相较FBMT算法省去多次前向平滑处理以及映射阵列的特征值分解,计算复杂度较低,运算时间相对较短。
4 结 论
针对现有基于完全相干信号的DOA估计算法阵列孔径损失严重,且在低信噪比环境下DOA计算精度较低的问题,提出了一种基于互质阵虚拟阵列空间平滑的DOA估计算法。该算法将互质阵列进行空洞填充,协方差矩阵按照波程差大小重构Toeplitz矩阵,然后再通过后向空间平滑算法二次构建Toeplitz矩阵,利用构建的与信号子空间最大信号特征值相关的代价函数来搜索谱函数,得到DOA。该算法优点如下:
(1) CASS算法在比FBSS、FBMT、SWSS算法少阵元的条件下完成了比以上算法更准确的相干信号的DOA估计。同时,CASS算法估计精度又高于同所需阵元数相同的ML算法。CASS算法系统架置成本低、部署灵活,且计算复杂度低、性价比高;
(2) CASS算法在低快拍数、低信噪比环境下对完全相干、部分相干信号DOA估计精度更高,具有更好的鲁棒性;
(3) CASS算法估计相干信号DOA时,不需要信源数先验信息,更符合实际应用环境。
由于互质阵列虚拟阵列法在信号分离时利用空洞填充,存在一定信号损失,且互质阵列虚拟阵列算法是在虚拟域内进行的二阶等价虚拟阵列信号处理,故该算法在较高信噪比环境下DOA估计精度逊色于FBMT算法、SWSS算法。高信噪比条件下CASS算法的DOA估计精度仍存在提升空间。

