基于心脏形调制磁信号的目标定向机理

向枫桦, 杨宾峰, 李 博, 赵 震, 郭娇娇

(空军工程大学信息与导航学院, 陕西 西安 710077)

0 引 言

定位,就是确定目标的方位、距离所对应的位置信息。随着时代的进步和科技的发展,催生出了诸多导航定位手段,例如无线电导航定位、卫星导航定位、惯性导航、视觉导航等。无线电导航定位通过向空中辐射无线电信号,目标接收该信号经过解算实现定位,但无线电信号容易被干扰和欺骗,使得在一些极端情况下目标定位精度较低甚至无法进行定位。全球定位系统(global positioning system,GPS)是目前应用非常广泛的一种导航定位方式,其定位精度高,但在水下和地下等特殊场所的应用面临许多挑战。惯性导航依靠陀螺仪和加速度计经过解算实现位置的测量,但存在误差累积的不足。视觉导航感知环境信息数据量大,导航技术还不够成熟。而磁场信号具有穿透性强、抗干扰能力强等优势,已经应用在诸多方面。目前,人工磁场信号可由磁信标和通电螺线管产生,利用人工磁信标进行空间运动目标的定位是一种新的思路,该方法不需要基准地磁数据库,其抗干扰能力强,隐蔽性好,应用非常方便,具有广阔的应用前景。

基于磁信标的定位方法,国内外专家学者提出了不同的磁信标定位模型,定位的效果也各有差异。在国内,张朝阳等推导了基于磁性目标的磁偶极子模型的目标磁梯度张量定位算法,提出了利用一个测点的测量值来定位磁性目标的方法。王光源等利用潜艇模型,分析了磁梯度张量定位方法对目标的定位误差,证明了该方法在潜艇定位中的可行性。李光等分析了磁梯度张量定位方法存在的问题,对磁梯度张量定位公式进行了推导计算,提出磁梯度张量目标定位改进算法,设计了一套平面式磁梯度张量测量系统。Huang等人提出一种基于简化磁场模型的磁定位方法,通过使用4个固定在地面的三轴磁力计,从而估计出埋藏在地下的低频磁线圈的位置。在国外,Nara等人通过磁通门传感器阵列之间的差值测量目标位置磁感应强度三轴分量值及梯度张量的6个分量实现位置解算,但该方法在远程定位定向过程中实用性较差。Alan等人在地面放置多个甚低频电磁波信号发射器,接收端在地下接收到地面发射器的电磁信号后,可以确定出载体的位置。Haverinen等人提出了一种基于磁指纹的蒙特卡罗区域定位技术,利用无线可穿戴磁力仪成功地进行了人体自我定位实验。Davic等人参考GPS的空间布置,在空间上布置多个磁信标,通过计算目标点与磁信标的相对位置关系,得到了目标的位置坐标。目前国内外在磁信标定位所采用的方法上,都存在一些不足。例如,不论是基于磁梯度张量还是基于磁场强度,都是采用检测磁信号的幅值实现对目标的定位。然而,幅值的测量很容易受到外界信号的干扰,使得测量误差较大,最终造成定位的精度很低。目前,国内外在磁信号的相位方位研究很少。Nathan等人提出机械天线的概念,打算利用旋转永磁体来产生调制磁场。许多学者通过诸多实验验证该想法的可行性,并将其应用在通信系统中,但是目前没有任何研究将其用在测角系统。

本文基于心脏形调制磁信号定向技术,研究了心脏形调制磁信号的实现方式及定向机理。在不需要已知环境磁场的前提下,利用永磁体和通电导线合成心脏形调制磁信号,并研究不同距离调制磁信号的效果。为改善远距离心脏形调制磁信号的效果,提出一种椭圆和“8字形”的改进型合成方法,能够明显改善心脏形调制磁信号的性能,并进行不同距离的定向研究。最后,在实验室中利用永磁体在当地产生的磁场来验证调制磁信号相位式测角的可靠性和可行性。该方法不采用传统的幅值,而是采用调制信号进行定向研究,不存在多值性,无需知道被测物体的当地磁场情况,能够提高永磁体定位系统的鲁棒性。

1 无线电相位式测角原理

1.1 天线水平心脏形方向图

根据文献[27-28],三维方向图是以天线某点为中心,远区某一距离为半径作球面,根据球面上各点的电场强度模值与该点的方向角绘出的图形。二维方向图是由三维方向图取某个剖面而得到。水平心脏形方向图,顾名思义,就是三维方向图取水平剖面的形状是心脏形图形。水平心脏形方向图天线的方向性函数为

()=1+sin, 0<≤1

(1)

式中:为波束宽度;为调制度。

水平心脏形方向图可利用“8”字形方向图与圆形方向图组合形成,其中“8”字形方向图是由()=sin产生,圆形方向图是()=1产生,两者的合成仿真结果如图1所示。

图1 心脏形方向图形成原理Fig.1 Principle of heart-shaped directional diagram formation

在图1中,水平心脏形方向图在空间上具有唯一的最小值,出现在180°方向,也就是应用在测角系统中,将会出现单峰信号,不会出现测角的多值性问题。

1.2 旋转天线方向图测角原理

通过旋转心脏形方向图的方式(一般是顺时针),可以在空中形成包含方位信息的调制信号,该调制信号可以与目标点构成一一对应的关系。如图2所示,当心脏形方向图的最小值转到正东时,地面发射一个基准信号。通过测量调制信号与基准信号的相位差,即可测量出目标点的相对方位关系。

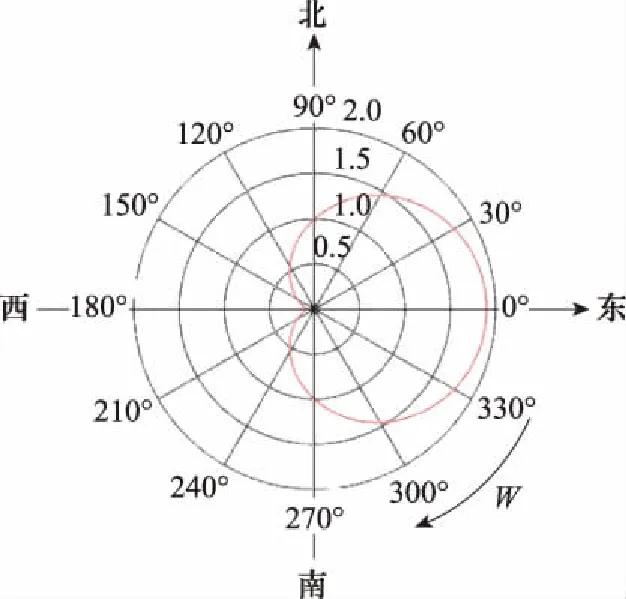
图2 测角原理图Fig.2 Diagram of goniometry schematic

2 心脏形调制磁信号测角机理

2.1 永磁体磁场分布

永磁体常见的形状有长方体、圆柱体、球体,无论是哪一种形状,在永磁体的轴向截面上都会产生一个“8”字形的磁场。这种“8”字形磁场与永磁体的形状、大小、材料都无关,并随着距离的增加,“8”字形磁场形状仍然保持不变。在Comsol软件中,仿真一个长度为40 cm、半径为5 cm的永磁体,得到永磁体的二维等势面模拟仿真图,如图3所示。

图3 永磁体磁场分布图Fig.3 Magnetic field distribution diagram of permanent magnets

由图3可知,永磁体周围产生的磁场是“8”字形磁场,距离永磁体越近,等势线越密集,磁场强度越大。

2.2 通电导线磁场分布

丹麦物理学家奥斯特用实验证实通电导线(直流电)周围存在磁场,并且通电导线周围的磁感线是以导线为圆心的同心圆,这些同心圆都与导线相互垂直,这意味这通电导线能够产生与距离无关的圆形磁场。在Comsol软件中,仿真一个30匝、电流为1 A的圆柱形均匀多匝导线,得到均匀多匝导线模型产生的二维等势面模拟仿真图,如图4所示。

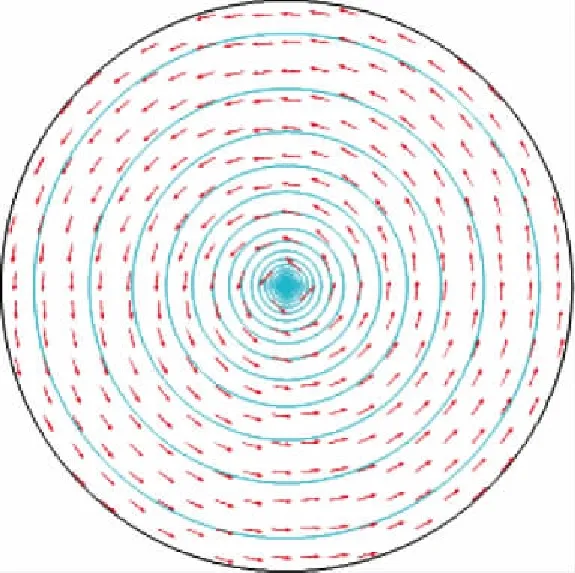
图4 通电导线的磁场分布图Fig.4 Magnetic field distribution diagram of energized wire

由图4可知,通电导线周围产生的磁场是圆形磁场,这些半径不一的圆都是以通电导线为圆心的同心圆,离通电导线距离越近,等势线越密集,磁场强度越大。

2.3 测角机理

下面借鉴无线电相位式测角原理,提出磁场相位式测角机理。当心脏形磁场最小值对准正东方向时,地面在正北方向发射一个全方位的基准电信号。如图5所示,永磁体以固定频率匀速旋转,每当心脏形磁场最小值对准正东方向,也就是0°方向时,地面在正北方向发射一个全向基准电信号,也就是图中的90°方向。通过测量基准信号与最小值之间的时间差,就可以计算出相对方位关系:

=×360°

(2)

式中:为永磁体旋转频率;为基准信号与最小值之间的时间差。

图5 基准信号与调制信号的相对关系Fig.5 Relative relationship between base signal and modulating signal

在图5中,当心脏形磁场最小值对准正东方向时,地面在正北方向发射一个全方位的基准信号。

3 仿真实验

3.1 永磁体与通电导线的合成磁场

通过前面的分析,永磁体能够产生“8”字形磁场,均匀多匝导线能够产生“圆形”磁场,按照天线心脏形方向图的形成原理,可以将永磁体与均匀多匝导线模型结合,在空间上产生一个心脏形调制磁信号,这样就消除了永磁体“8”字形磁场相位的多值性,可以将永磁体用在调制信号测角系统中。在Comsol软件中,在距离永磁体和均匀多匝导线模型50 m、60 m、70 m、80 m、90 m、100 m处分别测量磁场的大小和方向,得到的数据在Matlab中进行矢量叠加,得到对应的调制信号如图6所示,极坐标图(选取具有代表性的50 m和100 m)如图7所示。

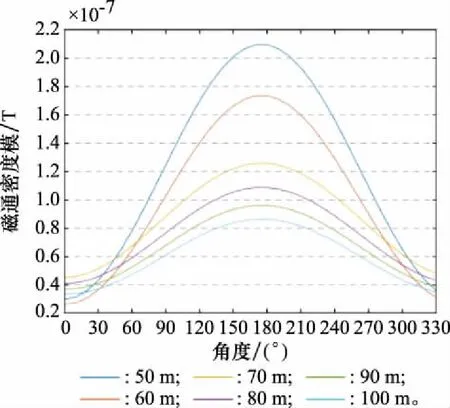
图6 不同距离的调制信号分布图Fig.6 Distribution diagram of modulated signals at different distances

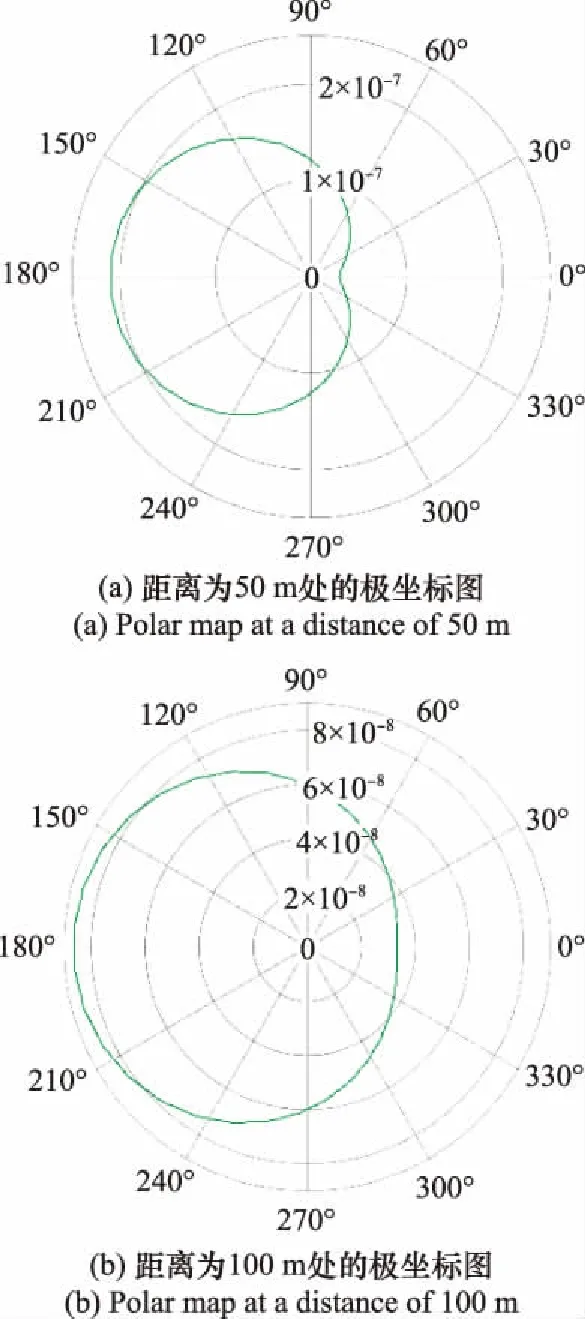
图7 极坐标分布图Fig.7 Polar coordinate distribution

在图6中,随着距离的增加,虽然磁场的大小是不断减小,但是调制信号依然具有一个最大值和一个最小值,分别出现在0°和180°方向,依然是单峰值信号,可以应用在相位式测角系统中。

在图7中,50 m处的磁场分布是心脏形图形,在0°方向具有唯一的最小值,在180°方向具有唯一的最大值;100 m处磁场分布接近圆形,心脏形效果不明显。

3.2 改进型的合成磁场

随着距离的增加,心脏形磁场分布越来越不明显,因此下面采用椭圆加“8”字形的矢量叠加方法,将通电导线由轴方向依次向轴正方向倾斜10°、20°、30°、40°、50°、60°、70°、80°,此时通电导线在原测量阵上产生的磁场是椭圆形状,保持测量阵不变,再将两者的磁场进行矢量叠加,得到的磁场调制信号如图8所示(选取具有代表性的10°、20°、30°、40°、50°数据),选取效果最好的倾斜30°的磁场极坐标图如图9所示。

在图8中,当通电导线向y轴正方向倾斜30°时,合成磁场有非常明显的变化,虽然出现了两个高峰,但是此时是心脏形最佳的时候,也就是更加适合用在最小值测角中。随着倾斜角度的增加,合成磁场甚至出现了两个低峰,显然就不适合用在相位式测角系统中。

图8 不同角度的调制信号分布图Fig.8 Distribution of modulated signals from different angles

图9 倾斜30°的极坐标分布图Fig.9 Distribution of polar coordinates tilted at 30°

从图9中可以看出,通电导线向轴正方向倾斜30°时,出现了非常明显的心脏形,唯一的最小值仍然是在0°方向。在实际应用中,如果心脏形磁场不明显,可以通过调整通电导线的倾斜角度来实现心脏形磁场信号。

3.3 一般型与改进型的合成磁场对比

选择距离永磁体100 m处,保持磁力仪的位置不变,固定永磁体的旋转频率为20Hz,此时在100 m处的磁力仪将会接收到调制磁场信号如图10所示。

图10 两种方式产生的磁场对比Fig.10 Comparison of magnetic fields generated by two methods

在图10(a)中,改进型的心脏形磁场出现两个最大值,一个最小值,相对一般型的磁场来说,最小值更小;在图10(b)中,改进型心脏形磁场非常明显,非常适合用在最小值的相位式测角系统中,但是磁场大小明显减小,牺牲了磁场的作用距离。

3.4 测角仿真

永磁体的旋转频率为20 Hz,在距离永磁体50 m、60 m、70 m、80 m、90 m处任意各取一点,分别为(3117,3909)、(5151,3077)、(3741,4691)、(4988,6255)、(5611,7036)、(6235,7818),单位为m,让永磁体以固定频率匀速旋转,记录调制信号数据,以点为例,得到的磁场调制信号如图11所示。

图11 磁场调制信号分布图Fig.11 Diagram of magnetic field modulation signal distribution

在图11中,每当心脏形磁场旋转一周,将会收到一个基准信号,并且旋转生成的调制信号是具有周期性的。

通过测量最低峰与最接近该点的基准信号的时间差,通过式(1)即可测量相对方位关系,得到目标点的实际方位与测量方位如表1所示。

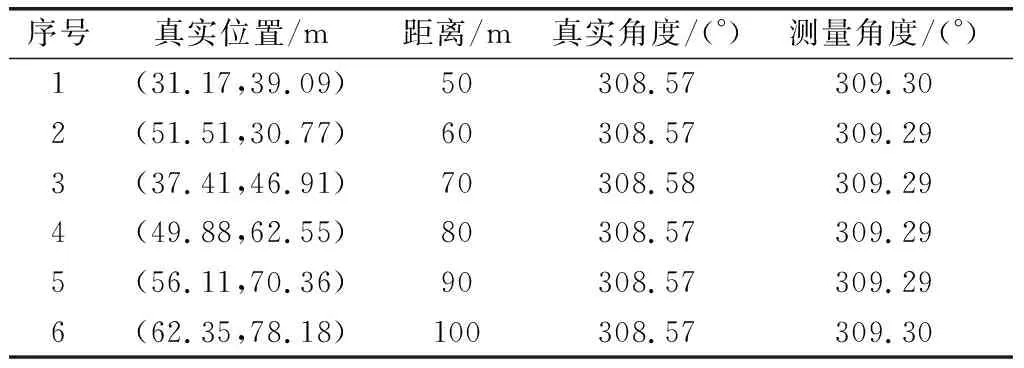
表1 不同距离下的测量角度对比Table 1 Comparison of measurement angles at different distances

显然,随着距离的增加,真实角度与测量角度之间的平均误差保持在0.72°左右,也就是说距离对相位式测角的影响很小。

4 实验验证

实验系统由无磁转台和数据采集系统两部分组成,无磁转台如图12所示,由内框、中框、外框3部分组成,通过旋转这3个框,可以改变永磁体的方位角、横滚角和俯仰角,永磁体的参数为半径为1 cm、高度37.5 cm,材料为N38钕铁硼。软件部分如图13所示,由PC端、数显管、三轴磁通门计组成和磁力仪4部分组成。其中,数显管显示无磁转台的内框、中框、外框的角度值,磁力仪可以测量磁场的三分量的大小,三轴磁通门计显示磁力仪的数据,PC端可以显示数显管、三轴磁通门计的数据,可以进行单点储存或者连续储存。

图12 无磁转台Fig.12 Non-magnetic rotary table

图13 数据采集系统Fig.13 Data acquisition system

由于实验室没有通直流电的导线模型,下面用永磁体在当地产生的磁场来验证磁场相位式测角的可行性。

实验步骤如图14所示,首先,调整无磁转台的内框、中框、外框,使三框归零并给设备加上电源;其次,设置转台串口为COM4、磁力仪串口为COM5、采样频率为20 Hz;然后,为了研究旋转磁场测角的可靠性,研究相位是否超前和落后,因此设置磁力仪与无磁转台的角度,分别位于0°、330°、30°方向,并按照设置频率转动无磁转台,同时在数据采集系统中记录相应数据;最后,将采集的数据在Matlab中进行处理(采用一个周期的数据分析),得到的仿真图如图15所示。

图14 实验步骤Fig.14 Experimental steps

图15 不同角度的实测信号Fig.15 Measured signals at different angles

图15中,在幅值方面,当磁力仪位于无磁转台的0°方向时,磁场的最大值稍微大于其他两个角度,30°方向和330°方向的磁场最大值十分接近,三者的最小值十分接近,可以得出角度对磁场的最小值影响不大的结论。在Matlab中,选取信号在相邻上升沿的最大值来比较相位。在相位方面,当磁力仪位于无磁转台的30°方向时,相位超前磁力仪位于无磁转台的0°方向时的相位,角度为30.55°;当磁力仪位于无磁转台的330°方向时,相位落后磁力仪位于无磁转台的0°方向时的相位,角度为30.54°。因此,永磁体可以应用在相位式测角系统中,间接验证心脏形调制磁信号是可以用来进行角度测量的。

5 结 论

本文提出一种基于心脏形调制磁信号的相位式测角机理,首次利用磁信号的相位信息进行测角。首先,将永磁体产生的磁场和通电导线产生的磁场进行空间合成,生成心脏形调制磁信号,解决永磁体存在双峰值的不足。其次,研究不同距离对心脏形调制磁信号的影响,发现随着距离的增加,虽然调制信号心脏形越来越不明显,但是仍然是单峰信号。然后,提出改进型方案来改善远距离心脏形磁场不明显的不足,并对不同距离下的随机目标点进行测角,角度平均误差保持在0.72°左右。最后,在实验室利用永磁体在当地产生的磁场验证磁信号相位式测角的可行性。本文提出的方法不采用传统的幅值进行测量,而是采用调制磁信号的相位进行定向研究,无需知道被测物体的当地磁场情况,由于只利用磁信号的相位信息,不在乎幅值大小,因此该方法抗干扰能力强,可以应用复杂电磁环境中。另外,在实际应用中,可以应用在近距离的目标定向中,例如无人机的室内导航、室内车辆的导航定位等等。