基于核心素养下“传送带模型”的教学策略


摘要:滑块在传送带上运动的情形称为传送带模型.因为物块与传送带之间存在动摩擦因数,传送带水平、传送带倾斜,传送速度、传送方向,滑块的初速度大小和方向的不同,使得传送带问题存在多样性、复杂性,对传送带问题能做出准确的动力学过程分析,是解决传送带问题的关键,而动力学的过程分析,需要对摩擦力有准确的判断,因此传送带模型中对摩擦力的判断是整个问题的重点和难点.
关键词:传送带;摩擦力;核心素养
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2022)09-0088-03
收稿日期:2021-12-25
作者简介:刘泽法(1988.10-),男,福建省宁德人,中学一级教师,从事高中物理教学研究.
传送带问题在日常生活生产情景中经常出现,如飞机场、火车站、客运站过安检时,货物的传送沙石、大米等.所以具有以真实物理情境为前提,结合牛顿定律,高度理论结合实际的特点,是一种综合的题型,具有提高学生的思维能力,又能学以致用解决实际问题,体现了核心素养中物理观念的运动与相互作用,需对物体不同过程受力分析,由牛顿第二定律求出对应过程的加速度,从而进一步分析物体的运动过程,及科学思维中传送带模型构建,临界极值思维,科学推理科学论证,不同过程受力与运动的变化,两过程运动参量的计算与联系.
1 要对传送带上的物体受力分析
受力分析最难的点在于摩擦力,是静摩擦力还是滑动摩擦力,方向如何学生往往晕头转向,所以要帮助学生掌握物块与传送带之间是否存在摩擦力,是滑动摩擦力还是静摩擦力,方向如何等基本知识点.在解决其问题上,当物块的速度v变至跟传送带的速度v一样时,往往是滑动摩擦力f从有到无;由滑动摩擦力f变成静摩擦力f;摩擦力方向发生变化的临界状态.主要可概括成以下三种情形.
1.1 滑动摩擦力从有到无,只发生在水平传送带情景下
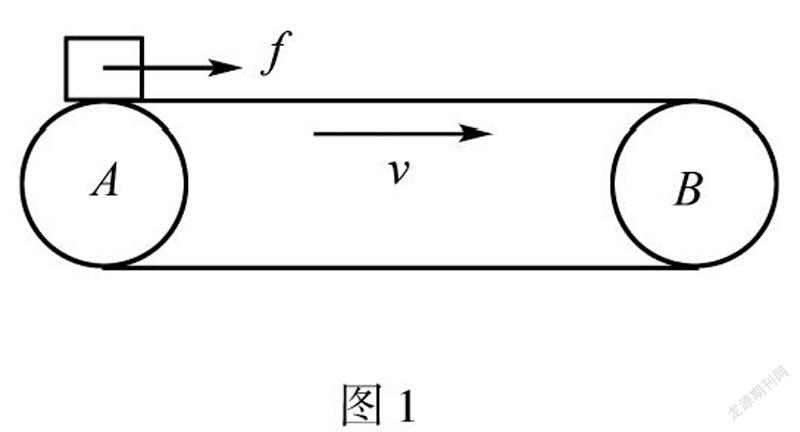
如图1所示,把初速度v=0的物体放在顺时针水平转动传送带的左端,物体受到水平向右的滑动摩擦力,在水平向右的摩擦力作用下做初速度v=0,加速度a=μg的匀加速直线运动.当物体速度v加速到跟传送带速度v相等时,物体与传送带不发生打滑,是滑动摩擦力f从有到无的临界状态.
1.2 滑动摩擦力f突变成静摩擦力f的情况
如图2所示,把初速度v=0的物体放在在顺时针转动倾斜的传送带下端,这种情况下一定是μ>tanθ,物体受到竖直向下的重力mg,垂直传送带向上的支持力N及沿传送带斜面向上的滑动摩擦力f,且滑动摩擦力f=μmgcosθ大于重力沿传送带向下的分力G=mgsinθ,所以物体做初速度v=0,加速度为a=μgcosθ-gsinθ的匀加速直线运动,当物体的速度v加速到跟传送带的速度v一样时,物体与传送带不打滑,由于最大静摩擦力f=μmgcosθ大于重力沿传送带向下的分力G=mgsinθ,所以物体与传送带相对于静止.物体受到的滑动摩擦力f就“突变”为静摩擦力f,方向沿传送带向上,大小为f=mgsinθ.
1.3 滑动摩擦力f方向突然发生变化
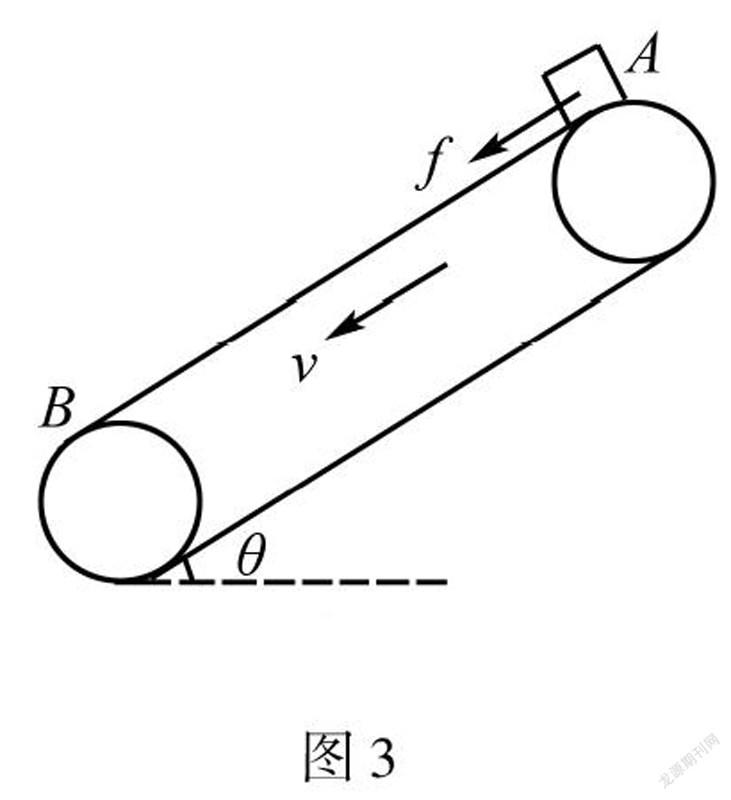
如图3所示,把初速度v=0的物体放在逆时针转动的倾斜的传送带上端,物体做初速度v=0,加速度为a=μgcosθ+gsinθ的匀加速直线运动,当物体的速度v加速到跟传送带v一样时,需考虑两种情况,若μ≥tanθ,即滑动摩擦力f=μmgcosθ大于重力沿传送带向下的分力G=mgsinθ,物体受到的滑动摩擦力f“突变”成静摩擦力f,方向沿传送带向上,大小等于f=mgsinθ.若μ<tanθ,即滑动摩擦力f=μmgcosθ小于重力沿传送带向下的分力G=mgsinθ,物体无法与其相对静止,滑动摩擦力f方向发生变化,变成沿斜面向上,大小为f ″=μmgcosθ.
总之,传送带问题中物块速度与传送带速度相同时是解决问题的关键所在,是滑动摩擦力f消失等于零,是滑动摩擦力f改变方向,是滑动摩擦力f突变为静摩擦力f的临界条件.
2 要对物体的运动过程及各个过程运动性质进行分析
传送带问题,通常是多过程的运动,各个过程之间又是连贯的,物体和传送带达到共速时刻,是各个运动交接的临界点.要分析物体各个不同的运动过程及运动性质,共速是一个关键的切入点.要注意讲解以下四种复杂运动过程及性质.
如图3所示,把初速度v=0的物體放在逆时针匀速转动,速度大小为v,倾斜角为θ足够长的传送带上端,物体先做初速度v=0,加速度大小为a=μgcosθ+gsinθ沿传送带向下匀加速直线运动,当物体的运动速度加速到跟传送带速度一致时,此时摩擦力会突变,所以要分析清楚下个运动过程的性质.若μ≥tanθ,当物体的速度v加速到跟传送带速度v一样时,滑动摩擦力f“突变”为方向沿传送带向上静摩擦力f,此时物体受力平衡相对传送带静止,物体再以速度v向下做匀速直线运动.若μ<tanθ,当物体的速度v加速到跟传送带速度v一样时,滑动摩擦力f“突变”为方向沿传送带向上的滑动摩擦力f″=μmgcosθ,物体以新的加速度a=gsinθ-μgcosθ继续做匀加速直线运动.
如图4,把初速度为v≠0的物体放在逆时针匀速转动,速度为v,倾斜角为θ足够长的传送带A端,如果物体v>v,(物体v<v,情况如1,故不在阐述)若μ<tanθ,物体做初速度为v,加速度大小为a=gsinθ-μgcosθ的匀加速直线运动.若μ=tanθ,
物体做速度为v的匀速直线运动,若μ>tanθ,物体先做初速度为v,加速度大小为a=μgcosθ-gsinθ的匀减速,当物体的速度v减速到跟传送带v一样时,方向沿传送带向上的f=μmgcosθ“突变”为方向沿传送带向上的f=mgsinθ,此时物体受力平衡,物体和传送带相对静止,物体再以速度v向下做匀速直线运动.
如图2所示,把初速度v=0的物体放在顺时针匀速转动,速度为v,倾斜角为θ足够长的传送带下端,此情况一定μ>tanθ,物体先做v=0,加速度大小为a=μgcosθ-gsinθ的匀加速直线运动,当物体的速度v加速到跟传送带速度v一样时,方向沿传送带向上的f=μmgcosθ“突变”为方向沿传送带向上的f=mgsinθ,此时物体受力平衡,物体和传送带相对静止,物体再以速度v向上做匀速直线运动.
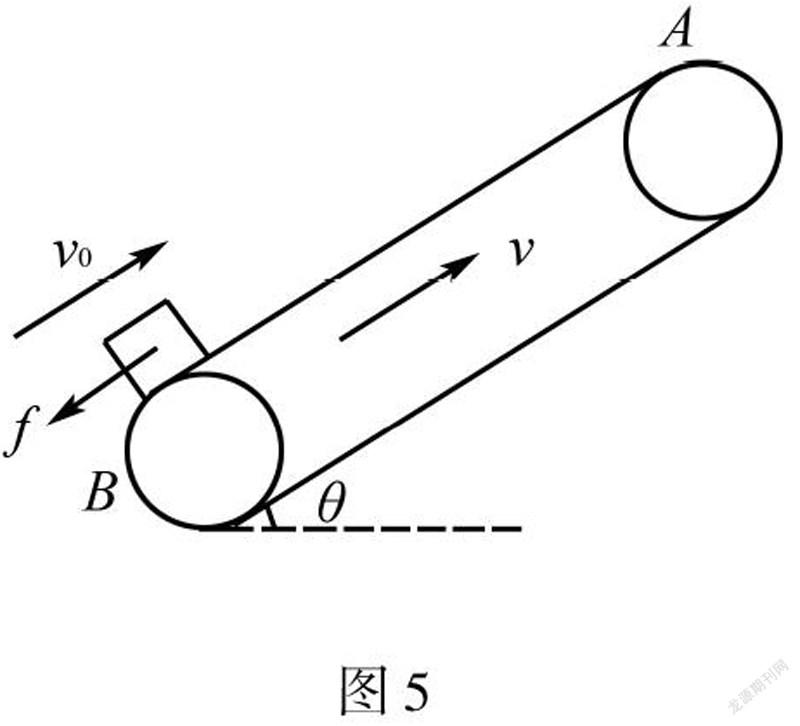
如图5所示,把初速度为v≠0的物体放在顺时针匀速转动,速度为v,倾斜角为θ足够长的传送带B端,如果物体v>v传,(物体v<v,情况如3,故不在阐述)物体受到竖直向下的重力,垂直传送带向上的支持力及沿传送带斜面向下的滑动摩擦力.物体先做初速度为v,加速度大小为a=μgcosθ+gsinθ的匀减速直线运动.若μ≥tanθ,当物体速度v減小到跟传送带速度v一致时,方向沿传送带向下的f=μmgcosθ“突变”为方向沿传送带向上的f,大小等于mgsinθ.此时物体受力平衡,物体和传送带相对静止,物体再以v向上做匀速直线运动.若μ<tanθ,当物体速度v减小到跟与传送带速度v一致时,方向沿传送带向下的f=μmgcosθ“突变”方向沿传送带向上的f ″=μmgcosθ,物体以新的加速度a=gsinθ-μgcosθ继续做匀减速直线运动,当物体的速度减速到零后,物体以加速度a=gsinθ-μgcosθ沿传送带斜面向下做匀加速直线运动.图5
通常,“传送带问题”涉及到物体的多个运动过程,不同的运动过程之间又是连贯的,物体和传送带达到共速时刻是不同运动过程的临界点,解题时应该分析清楚物体各个运动过程的受力状态和运动性质,在应用牛顿定律和运动学规律求解,下面列举例题加以说明.
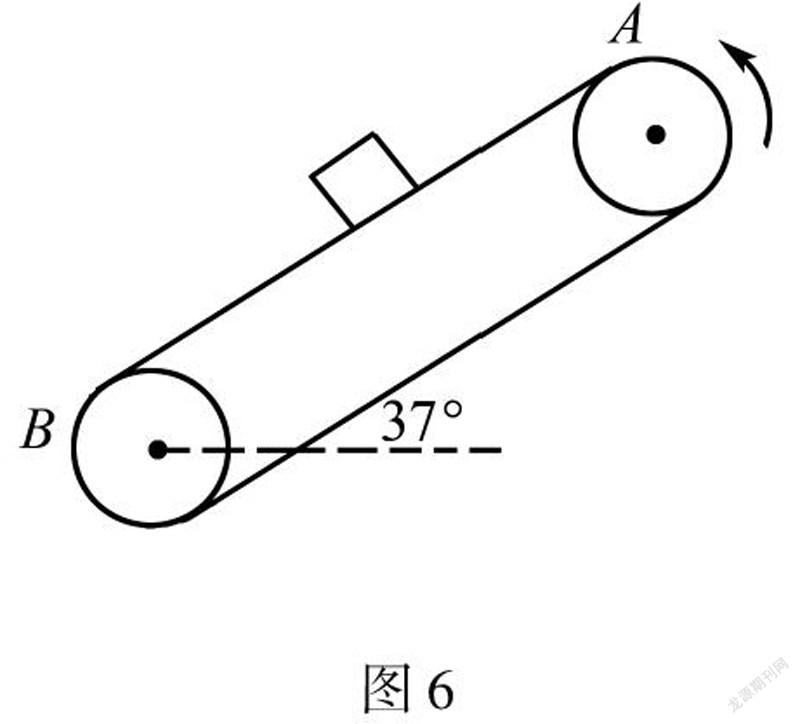
例题如图6所示,倾斜运输带AB与水平面成θ=37°,A点到B点的距离为L=16m,运输带逆时针运动,运行速率恒为v=10m/s,现在将一质量为m=0.5kg的物体轻轻放于A点,已知物体与斜面的动摩擦因数μ=0.5,求物体从A端运动到B端需要多长时间?(g取10m/s,sin37°=0.6,cos37°=0.8)
解过程一,物体做v=0的匀加速直线运动;

