公路路基生态排水沟室内模型试验研究

冯佳佳、朱登远、吴华、杨成业、张根

（1.西藏大学，西藏 拉萨 850000；2.肇庆市公路发展有限公司，广东 肇庆 526000）

0 引言

随着我国经济持续快速地发展，公路建设投资规模不断地加大，对工程质量的要求也越来越高。在已建成公路中路基路面的工程病害多种多样，形成病害的因素亦很多，其中排水沟的优劣是主要因素之一[1]。排水设施设计不合理一方面引起路基路面排水不畅，造成一些路段不同程度的水毁，另一方面大量污工砌体的采用又会造成极大的浪费和对公路沿线生态环境造成严重的破坏[2]。综上可知，进行公路路基路面排水设施设计优化研究是必要的。

1 试验模型设计

模型试验系统包括供水系统、模型试验区及排水系统（见图1）[3]。供水系统由储水池、水泵房、恒压水塔、流量控制装置及进水稳流设施组成，由水泵连续向水塔供水，水塔有恒压装置，恒压水流经管道流进流量控制装置，流量控制通过阀门和矩形堰来实现，然后通过消浪稳定后扩散为与试验沟槽同宽的稳定水流进入模型试验区[4]。模型试验的试验台总长18m，宽2.3m，其中铺草皮段长12.85m，宽2m，具体尺寸如图2 所示。

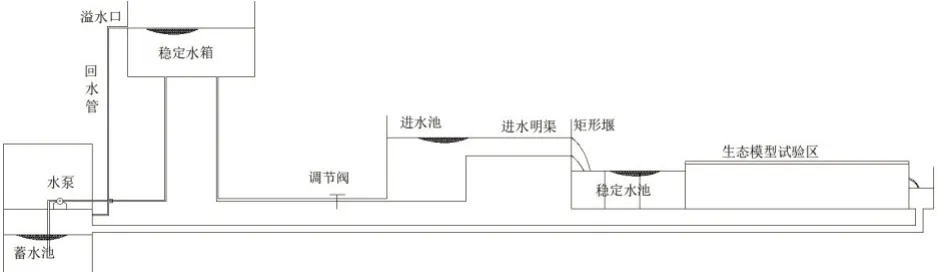
图1 模型试验系统组成

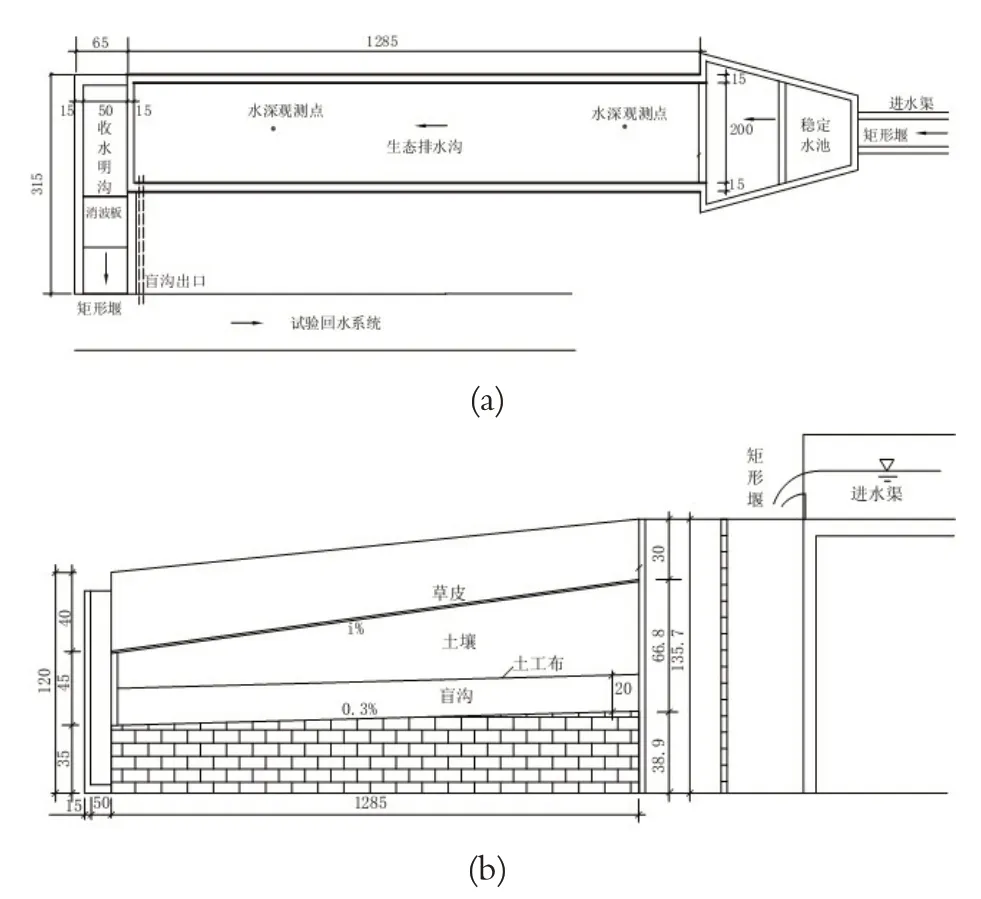
图2 模型试验区尺寸图

模型试验区主要测量不同流量下的上、下游断面的水深和宽度，出水分为两路，第一路由草皮浅沟的末端流出，进入收水明沟；第二路由草皮渗入土壤，并通过底部的盲沟流出。

室内模型试验采用的生态排水沟为抛物线型横断面，横断面的抛物线方程为：h=ax2。为减小模型试验误差，试验草皮沟的宽度、深度和坡度与公路排水工程实际基本吻合。沟宽2m，沟深20cm、30cm、40cm，坡度分别为0.3%、1%和2%。

2 试验测试内容和测试方法

在试验过程中，测试的参数主要有进水堰的水位、出水堰的水位和沟渠中两个断面的水深，此外还测出沟渠的水流宽度和地下水渗流量（盲沟）。入口流量和出口明沟的流量用矩形堰测流；盲沟出流较小，用体积法测流。为了保证堰前水流稳定，除矩形堰前必须有较长的均匀沟渠外，还设置两道消波板，尽可能减小水流波动引起的误差。浅沟内的水深用测针观测，以避免其他设备对水流的干扰。测针距离进口和出口有一定的距离，以观测两个位置的不同水深。平均流速则通过流量和过水断面面积推算[5]。

在试验中，每一种断面形式及坡度情况下，都测试8～12 个不同的流量。流量从小到大测一遍，再从大到小测一遍，每遍分4～6 级，使流量与沟内水深关系能点绘成有规律的曲线。试验中草皮的高度统一剪成5cm 左右。

3 试验过程和试验数据

3.1 前期准备

前期主要是按试模型设计试验尺寸修建了生态排水沟试验区，搭建供水系统，制作各种断面尺寸的模板，加工购置了堰板、测针等测试工具和仪器。

3.2 矩形堰的率定

为了保证精度，预先对矩形堰进行率定。入口矩形堰的率定采用体积法，出口堰的率定采用与入口堰对照法，并与根据理论公式（1）和（2）计算的结果比较，以减小误差。

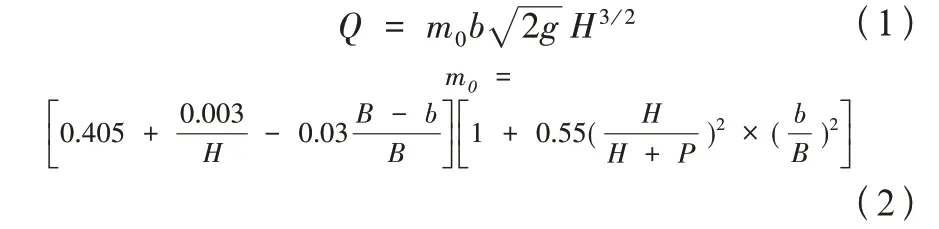
式（1）～（2）中：Q为流量（m3/s）；m0为流量系数；B为水面宽（m）；b为堰口宽（m）；H 为堰头水深（m）；P为上游堰高（m）。

体积法率定进水堰的方法是当堰头水深稳定时，测出一定时间内下游水池中增加的水的体积。时间用秒表记录，体积通过量测水池的长、宽及量测到的水深变化，按体积公式计算。测出多组不同堰头水深条件下的流量，绘出流量-水深变化图。

3.3 试验步骤

第一步打开水泵，使恒压水塔保证稳定水头；

第二步缓慢旋开进水阀门，水流稳定后通过测针量测出进水堰水深，该流量下的水流流经试验区一段时间后，水流趋于稳定，当沟槽上、下游测针及各出水堰的测针读数基本不变时，同时记下各测针对应的水深数据，并量测生态排水沟中的水面宽度（有必要时用秒表和量杯测出盲沟的出流量），作为一组数据；

第三步调节阀门大小，按步骤二，测出下一个稳定流量时各测针对应的数据；然后重复步骤二操作，测出8～12 组数据。流量先逐渐增大再逐渐减小；流量分布要相对均匀，同时不能使流量过大（不能超出水泵的供水能力，否则水塔不能保持恒压，试验误差就会较大）；

第四步测出测针零点读数，整理数据。

然后，调整纵坡或沟型，重新换土回填，整形、铺草皮，为下一组试验做准备。

3.4 试验数据处理

通过测针读数减去零点读数，得出各种情况下的水深数值；根据矩形薄壁堰堰流的理论公式和率定的系数，求出各堰头水深对应的流量；不考虑埋设PVC管时，沟中水流满足均匀流的条件，通过均匀流的流量计算公式可以反求出糙率，水深用生态排水沟中上下游水深的平均值，流量用出水堰流量计算[6]。

式（3）～（4）中：A为过水断面面积，对抛物线断面，(a 为抛物线方程的系数，当沟宽B=2m时，a等于沟深)。

式（5）～（6）中：

h为水深；

I为水力坡度，均匀流条件下为沟底纵坡。

4 试验结果分析

4.1 沟渠过水能力分析

将各种断面尺寸的抛物线型草皮沟在不同坡度下的流量、水深数据点绘在Q～H 坐标系中，用幂函数对这些点进行拟合，得出各种情况下的Q～H 关系曲线，如图3 所示。从图3 可以看到相关系在0.99 以上，说明试验的流量～水深数据相关性非常好，可以根据流量～水深曲线来判断宽2m，深20～40cm 的生态排水沟在不同坡度下的过水能力。本文仅以宽2m，深30cm 的生态排水沟为例进行结果分析。

图3 流量～水深关系（2m 宽、深30cm）

从图3 可以看出，同一坡度情况下，随着水深的增大，流量呈J 数增长。同一深度情况下，随着坡度的增大，流量也随之增大。

4.2 抛物线型草皮沟的糙率分析

4.2.1 糙率与水深的关系

将同种沟深、不同坡度情况下的糙率、水深数据点绘在n～h 坐标系中，糙率～水深关系曲线见图4。

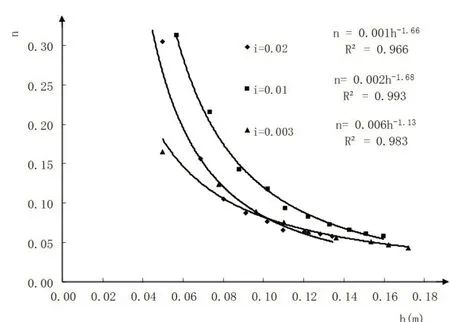
图4 不同坡度时的糙率～水深关系（宽2m，深30cm）

从图4 可以看出，断面相同时，随着坡度增大，设计最大水深时对应的糙率相应减小。

4.2.2 糙率与流量的关系

将同种沟深、不同坡度情况下的糙率、流量数据点绘在n～Q 坐标系中，同样用幂函数对这些点进行拟合，如图5 所示。

图5 不同坡度时的糙率～流量关系（宽2m，深30cm）

从图5 来看，生态排水沟的糙率随流量的增大逐渐减小，并且在流量较大时，糙率变化就非常小。

4.2.3 糙率与流速的关系

图6 不同坡度时的糙率～流速关系（2m 宽、深30cm）

总体上说，坡度相同时，不同的断面形状对n～v关系曲线的影响比较小，而且坡度越大，n～v 关系曲线越接近。同时可以提炼得出如下的经验公式和表3糙率取值范围。

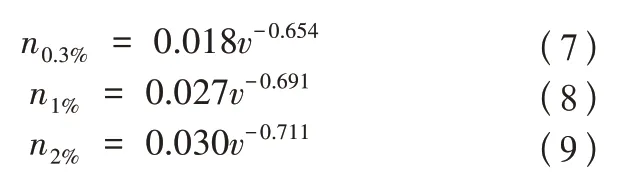
表3 抛物线型草皮沟的糙率取值（推荐）

5 结论

本文通过对公路路基排水系统进行室内模型试验，得出以下结论：

一是抛物线型草皮沟的流量～水深数据用幂函数拟合相关性非常好，相关系数均达到0.99 以上，表明抛物线型草皮沟的流量与水深间有显著关系，据此推算的草皮沟过水能力较可靠。

二是试验得出的抛物线型草皮沟糙率并不是一个常数，而是随水深、流量以及流速的变化而有所不同，并且变化范围比较大，因此，对抛物线型草皮沟的糙率选取一定要慎重。

三是纵坡不变时，不同沟深的糙率在流速相同的条件下变化不大，其变化范围在20%以内，据此结合公路生态排水沟建设实际拟合出了常见沟深在三种坡度下糙率与流速之间的经验公式，推荐了计算抛物线型草皮沟过水能力的糙率取值范围。