保险业承保风险引致系统性风险的复杂网络分析——基于寿险业与财险业的比较

自党的十九大报告首次提出要坚决打好防范化解重大风险攻坚战以来，中国保险业更加重视主动防范化解系统性风险。财险承保风险可以通过再保险业务的关联进行传递，从而存在引发保险业爆发系统性风险的可能性，那么寿险承保风险是否也是如此？“偿二代”5号文件明确指出，寿险业具有死亡巨灾风险，应计量死亡巨灾风险最低资本。可见，寿险承保风险也可能成为系统性风险的来源之一。全球新冠肺炎疫情中的寿险赔付经历基本证实了上述观点。泰国、英国和美国等为防止保险行业整体破产，坚决拒绝新冠肺炎的相关赔付。劳合社CEO约翰·尼尔更是将新冠肺炎疫情称为“保险史上的最昂贵事件”。这都印证了寿险承保风险也可能会引发系统性风险。基于上述背景，本文提出并拟解决以下三个问题：寿险承保风险是否可能引发系统性风险？相比财险承保风险，寿险承保风险对系统性风险的影响程度如何？在引致系统性风险的过程中，行业和公司层面的哪些因素在发挥作用？有关承保风险引致系统性风险的研究多使用复杂网络模型，因此，本文首先基于再保险业务数据构建承保风险网络模型，继而构建承保风险的动态传染模型，仿真模拟并测量各年份的系统性风险。另外，文献中主要基于主导因素和贡献因素分析系统性风险的成因，有关主导因素的分析集中于企业规模和互联性，有关贡献因素的分析则集中于杠杆率和流动性风险。本文结合上述文献，寻找系统性风险的影响因素。

一、承保风险网络模型及风险传染过程

(一)承保风险网络模型

假设保险系统中有家保险公司，包括原保险和再保险公司。这家保险公司之间因再保险业务的关联而构成承保风险网络。各家保险公司之间的再保险关联体现为矩阵。表示第家保险公司向第家保险公司分出的保费，和分别表示第家保险公司的总分入保费和总分出保费。

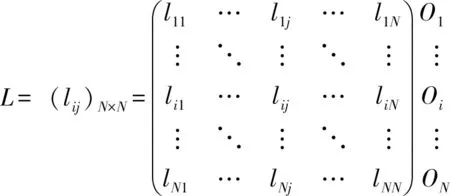
(1)

……

保险公司通常不公开详细的再保险交易数据，故只能根据总分入保费和总分出保费拟合再保险关联矩阵：根据保费收入和资产规模，利用K-均值聚类法将原保险公司划分为小型、中型和大型三类，并引入再保险公司，分别以=1、2、3、4表示。结合实务经验，假定同一规模等级内保险公司的安全性相近，并规定保险公司和再保险公司在办理再保险分出业务时具有明确的交易对手偏好，即保险公司只向安全性不低于自身的其他原保险公司和再保险公司分出，而再保险公司则仅向其他几家再保险公司分出。根据上述约束条件，构建如式(2)所示的再保险关联矩阵拟合模型，使用RAS算法求解再保险关联矩阵，模型的最优解即为寿险和财险承保风险网络。

构建“四驱双核”服务型教工党支部过程中工作载体的选择与创新，事关能否充分调动好教师党员的主动性、积极性和创造性成为“四驱”的原发力量，从而起到先锋模范带头作用；事关能否逐步打造成服务型教工党支部持续推进“双核”迈向纵深的阵地，从而筑牢党支部的战斗堡垒阵地功能；这就需要实现载体选择与创新的准确把握，将特色教工党支部建设与教师党员业务发展相联系，让教师党员对业务发展的热情、对时政理解与把握转化为服务学生培养上的具体行动，做到思想上同心，目标上同向，工作上同步。

2.2.1 表_User 表_User用于存放昆虫生境移动监测软件的用户数据，包括用户名username、密码password和手机号码mobilePhoneNumber等。

s.t.

min∑∑×ln()

∑=;∀∈{1,2,…,}

∑=;∀∈{1,2,…,}

2.10.2 分组、给药及血样采集[17] 取SD大鼠18只，雌雄兼用，随机分为3组，每组6只。于实验室环境中适应1 d，自由喝水。按10 mg/kg剂量分别ig给予大鼠Lut、Lut-SD和Lut-PC-SD混悬液。各组实验大鼠于0.15、0.5、0.75、1、1.5、2、4、6、8、12 h时间点眼眶取血约0.3 mL至肝素处理过的离心管中，并于转速为4 000 r/min条件下迅速离心3 min，分取上层血浆，转移至另一空白离心管中，−20 ℃冰箱保存。

本文样本期为2004—2018年，所有原始数据均来源于《中国保险年鉴》和保险公司官方网站。仅保留经营满一年及以上的公司，并剔除任意变量中含有异常值的公司。最终样本中，寿险和财险公司在各年份的总市场份额均达到90%以上，具有一定的代表性。

=0;∀>或=

通过上文的分析，对于大数据的到来对工程造价的意义有了一个充分的认识。明白了一个事物对于另一个事物的意义，下一步就是通过什么样的途径将二者结合起来，达到1+1＞2的最佳效果。对此可以从以下两个大的方面着手：

(2)

已有文献对承保风险网络模型的构建主要采用相对分散网络模型、相对集中网络模型及分层网络模型。本文模型属于分层网络模型，具有如下优点：(1)同时考虑了保费收入和资产规模来设定规模等级；(2)对再保险交易对手偏好的假设更符合实务经验；(3)使用K-均值聚类法对原保险公司进行规模等级划分，避免了主观赋值可能导致的不准确性。

本文将上面的移动互联网问题作为出发点，以目前的研究热点LISP协议为基础，设计出符合要求的网络虚拟化方案。

(二)承保风险传染过程的模拟

其中，(*)服从标准正态分布；为公司在第年风险传染过程中的表现，若无破产，则取值为1，否则取值为0；、、、、和分别表示公司在第年的赔付率、再保险分入率、再保险分出率、节点出度、节点入度和偿付能力；为控制变量。表2是上述各影响因素变量的含义和假设的影响方向。

外部环境带来的非预期损失冲击通常是引发系统性风险的导火线。本文研究目标之一是量化并对比财寿险承保风险对保险业系统性风险的影响，因此，在模拟时假设保险业首先处在样本年的稳态水平，外部损失冲击以当年赔付率的倍数逐渐递增，进而观察保险业的反应。传染过程如图1：

图2展示了承保风险和违约风险的传播路径。首先，保险系统处于稳定状态。当保险事故发生后，被保险人向原保险人提出索赔，原保险人面临“原保险赔款”损失，承保风险从系统外部传导给大、中和小型公司(见图2a)。然后，原保险人向各自的再保险分入人提出索赔，分入人支付分保赔款。若保险公司既是分出人又是分入人，则不仅可能收到“摊回分保赔款”，同时也得支付“再保险赔款”(见图1)。此时，承保风险从分出公司传导至相应的分入公司(见图2b)。综上，原保险公司的现金流出包括原保险赔款和再保险赔款，现金流入为摊回分保赔款；再保险公司的现金流出和现金流入分别是再保险赔款和摊回分保赔款。最终承保损失为现金流出减去现金流入的差。随后，判断最终承保损失是否超过支付阈值。若所有公司的承保损失都在支付能力范围内，则无违约行为发生，承保风险的传播结束；但若有一家或多家公司的承保损失超过其支付阈值，则对应的分出公司将遭受额外的“传染损失”(见图1)，此时，违约风险发生，并使传染损失从分入公司传导至分出公司(见图2c)。继而，判断这部分分出公司是否依然足以支付其承保损失。若都能继续全额支付，则传染风险发生的后果不会延续，传染过程停止；若这部分分出公司中，又有一家或多家公司不能继续全额支付索赔，则继续发生违约，发生新一轮的传染损失。同理，计算最新一部分被违约的分出公司所遭受的传染损失，并判断其是否依旧足以支付相应的原保险赔款和再保险赔款。若都能承担，则传染过程结束；否则重复上述过程，直至没有新的违约行为发生。最后，在传染过程结束后，记录发生破产的公司数量以及初始损失冲击强度。

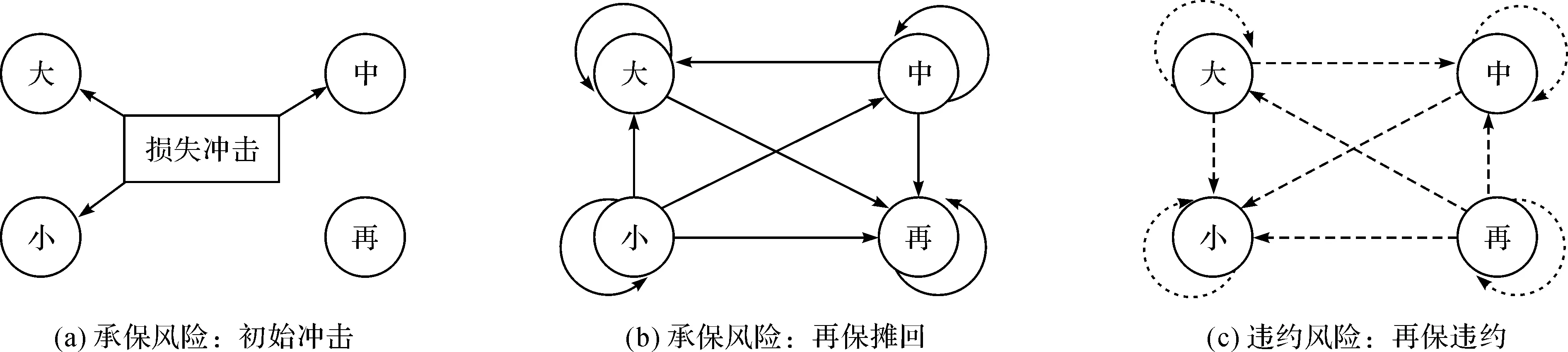
调整外部损失冲击强度，按上述过程模拟承保风险在保险系统的动态传播过程。当外部冲击较小时，所有公司都不会破产，模拟过程停止于“摊回分保赔款”阶段；当外部冲击逐渐增大时，开始出现一家公司破产，并引发微弱的传染损失；当外部冲击继续增大时，会出现多家公司同时破产，从而引发较大范围的传染损失，并进一步引发一轮又一轮的传染损失，触发多米诺骨牌效应。

“我娘跟我说了，我的妻子越秀逃了出来，但不知她会去哪里。我想，越秀去钱葱了。越秀喜欢吃钱葱，曾跟我说过几次，要我带她去吃，可惜她始终没能如愿。”

2.破产临界值的设定

赔付率：根据研究设计，平均赔付率越高，损失冲击越大，保险公司越易破产。故推测，在行业层面上，与行业平均赔付率()存在负相关关系。在公司层面上，公司自身的赔付率()是其承保业务风险管理能力的体现，赔付率越高，风险管理能力越弱。故推测，保险公司的赔付率()与其稳定性呈负相关关系。

(三)风险传染过程的各种损失核算

当外部损失冲击发生时，保险公司可能面临多项损失，下面对这些损失进行量化。假设保险系统遭受了倍平均赔付率的冲击，则保险公司可能会发生下列损失：

(1)原保险赔款()。公司在第年的保费收入为，平均赔付率为。若为原保险公司，则原保险赔款为=××；否则，=0。

“思雨，我过去的确是信任你的，而且我一直都在信任你，爱你。可我不相信这个社会了，我现在已经没有相信你的充分理论根据了。思雨，我们都应该冷静下来，重新思考生活、家庭、爱情了。你好好思考吧，你不能再欺骗我了。我们都好好想想，过两天再谈。”老婆的话像冰一样沉沉地砸在地板上。

(2)摊回分保赔款()。假设各公司均采用比例再保险，_为公司的分出比例，当损失发生时，公司从所有分入人处得到的摊回分保赔款之和为=_×。

(3)再保险赔款()。基于公司的分入业务，假设在第年公司向公司支付的再保险赔款为，则公司总计应承担的再保险赔款=∑。

(5)累计总损失()。综上，公司因原保险业务产生原保险赔款()，因分出业务获得摊回分保赔款()，因分入业务发生再保险赔款()，并因其他公司破产而遭受传染损失()。公司所面临的累计总损失为=-++。

资源保护是活化利用的根本前提和基础，活化利用是资源保护的目的和方向。以上数据表明，历史文化村镇保护随着时间发展和保护阶段的不断演进，在不同发展阶段会产生不同的问题，保护的重点也会稍有偏向和转移。

二、度量方法和研究设计

(一)系统性风险的衡量

在多冲击强度模型中，一般以系统损失率作为系统性风险的度量指标，偶尔也将传染违约机构达到10家或以上作为判断系统性风险是否存在的依据。考虑到寿险和财险的可比性并结合研究目的，将系统中25的保险公司破产时的损失冲击强度作为系统性风险的代理变量，并定义为。换言之，能导致25的保险公司破产的损失冲击强度()越大，说明保险系统的稳定性越高，系统性风险越小；反之亦反。因此，损失冲击强度()与系统性风险呈负相关关系。

(二)系统性风险的影响因素分析

1解释变量与预测方向

当公司遭受的总损失超过其支付阈值时，将面临破产并发生再保险违约，因此，破产阈值的设定对承保风险动态传播过程的模拟尤为重要。文献中多以所有者权益作为破产界限。然而，由于负债经营的特点，保险实务中存在不少权益为负却仍然正常运营的保险公司，因此，本文以流动性资产作为破产阈值。一方面，流动性资产能在短时间内变现，更适合用于应对突发的风险状况；另一方面，流动性资产与所有者权益的相关性很高，可以取代后者作为破产阈值。

再保险分入率：保险公司的再保险赔款是因分入业务而产生的。实务中，原保险公司的再保险分入业务具有比原保险业务更加突出的信息不对称问题。因此，再保险分入比例越高，保险公司面临的风险也将越大。故推断，再保险分入率()与保险公司的稳定性呈负相关关系，保险业平均再保险分入率()则应与系统性风险的代理变量存在负相关关系。

分组讨论法是以学生分组为基础单元，以教师拟定的讨论专题为对象，按照老师的指导查阅文献、研究分析问题并提出自己的观点，通过这种以问题为导向的自主互助学习，将学习的主动权交给学生的一种学习方法[4-5]。这种教学方法的最大优势是提高了学生的参与度和在教学中的地位，极大地激发了学生的学习兴趣，使学生的主体地位发生了根本性变化，将其以往教学中的被动接收知识方式转变为主动获取知识，在此过程中培养了学生主动参与、自主学习的能力，并提高了学生分析问题和解决问题的能力。由于在分组讨论中每个学生作为小组的成员要共同协作完成一个课题，因此营造了互助的学习氛围，也培养了学生的团队合作能力。

再保险分出率：承保业务的分出有助于降低保险公司的总损失，同时也会增加系统中其他保险公司的财务负担。故推测，再保险分出率()与保险公司的稳定性呈正相关关系，而行业平均再保险分出率()则与系统性风险的代理变量存在负相关关系。

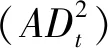
偿付能力：流动性资产越高于保费收入，则偿付能力越强，越不容易破产。若所有公司的破产条件都变得更苛刻，将更难爆发系统性风险。故推断，在行业层面，平均偿付能力()与存在正相关关系，在公司层面，公司的偿付能力()对其自身的稳定性有正向影响。

其中，、、和分别为第年的行业平均赔付率、平均再保险分出率、网络结构平均度和平均偿付能力。考虑到网络结构平均度的影响可能是非线性的，故同时考虑网络结构平均度的二次项。表1是上述各影响因素变量的含义和假设的影响方向。

以为被解释变量，上述分析的影响因素为解释变量，构建如下线性回归模型：

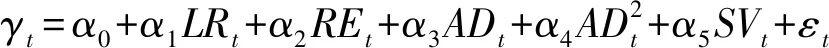
(3)

2基于行业层面的分析

老虎山河流域坡地占总体面积的84.3%，河谷平原只占15.7%。其特点是土壤松散、植被覆盖差，雨季河水涨落急剧，水土流失严重。

3基于公司层面的分析

同理，以特定保险公司在损失冲击下的具体表现为被解释变量，采用上述分析的各影响因素在公司层面的表现为解释变量，构建以下probit回归模型：

观察组与对照组理论部分成绩分别为（47.36±1.58）分、（39.47±4.05）分，实践成绩分别为（43.22±2.12）分、（37.14±5.56）分，观察组两项得分均高于对照组，差异具有统计学意义（理论：t=9.903，P=0.000＜0.05；实践：t=2.142，P=0.035＜0.05）。

prob(=1)=(+++++++′+)

(4)

1.承保风险在保险系统中的传播和传染

(三)数据来源与说明

≥0;∀,∈{1,2,…,}

三、实证分析

(一)承保风险网络的分析

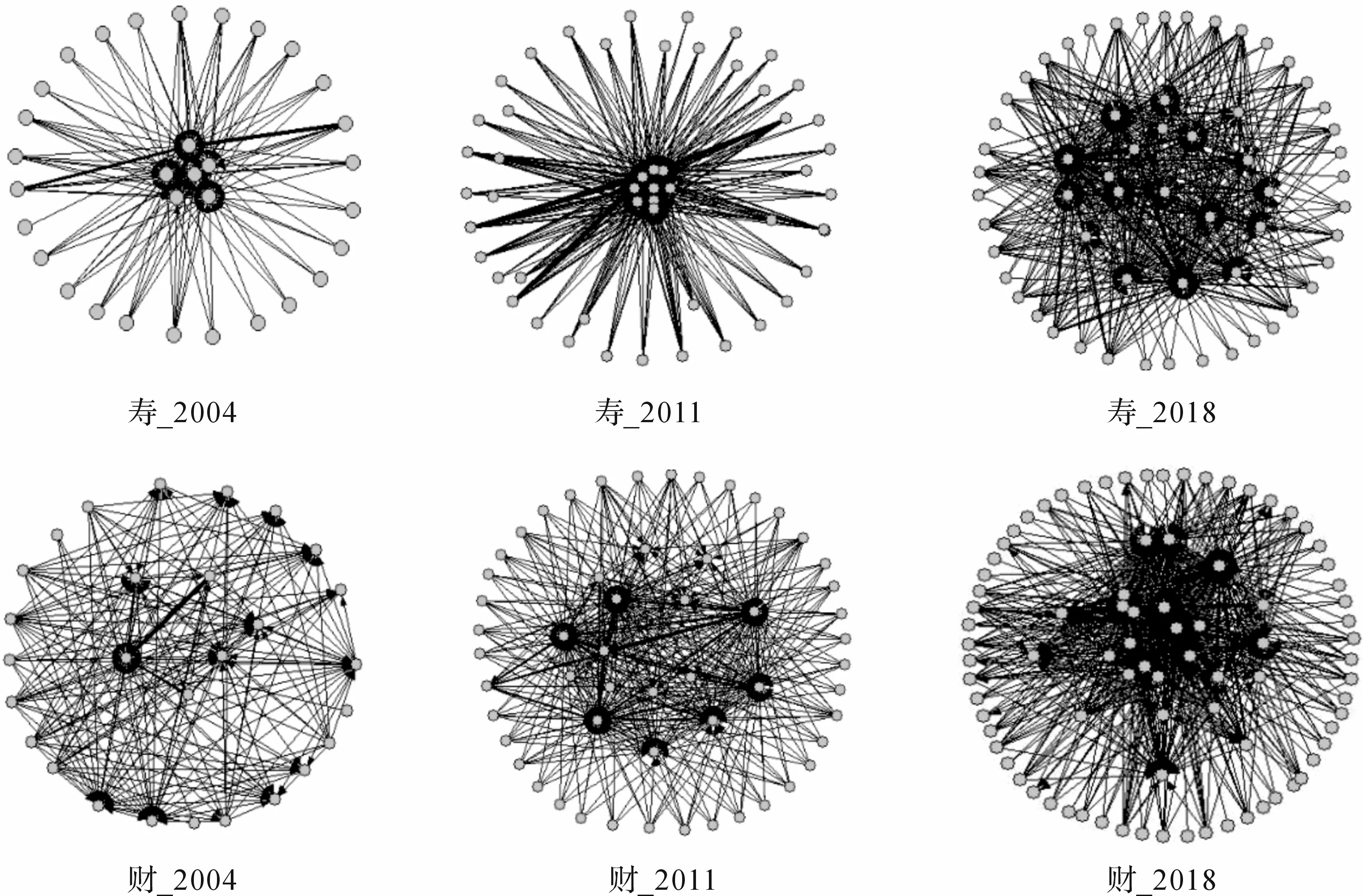
利用式(2)中的拟合模型构造各年寿险和财险承保风险网络结构。图3展示了两个行业在2004、2011和2018年的网络结构，图中每个节点均代表一家保险公司，节点之间的连线表示公司间的再保险关联关系，连线越粗则再保险关联关系越紧密。由图3不难发现，随着中国保险市场的快速发展，无论是寿险业还是财险业，保险公司之间的联系都更加紧密，保险承保风险网络的紧密度不断增加。但在任意样本年，寿险公司之间的联系紧密程度均明显低于财险公司。

(二)系统性风险及其差异

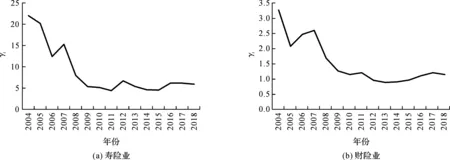
样本年变化趋势如图4所示。总体上，系统性风险的代理变量在寿险和财险业中都呈下降趋势，但均在2010年后趋于平稳。根据理论模型分析，与系统性风险具有负相关关系，意味着寿险和财险承保风险所导致的系统性风险呈逐年上升趋势，但自2010年起，承保风险导致的系统性风险基本保持稳定，无显著上升趋势。此外，寿险承保风险导致的系统性风险水平整体上显著小于财险。这一结论与现实相符。财险业务的保障性更强，而寿险业务投资性较为突出，因此寿险承保风险导致的系统性风险水平低于财险。

(三)承保风险引致系统性风险差异的影响因素分析：基于行业层面

1影响因素的回归分析

表3汇报了系统性风险影响因素的回归结果。表3中各变量的影响方向和显著度在不同模型中均一致。平均赔付率()和平均再保险分出率()对的影响显著为负。依据与系统性风险间的负相关关系，则平均赔付率()和平均再保险分出率()对承保风险所导致的系统性风险具有正向影响，即行业平均赔付率和平均再保险分出率的增加都促使系统性风险上升。网络结构平均度()的一次项和二次项系数分别显著为负和显著为正，说明网络结构平均度()对存在正U型影响。当系统联系很弱时，承保风险的传染渠道被截断，溢出效应低，系统性风险也较低；当联系逐渐增强时，承保风险得以快速传染，溢出效应增加，系统性风险也快速增加；当联系增加到一定程度时，承保风险的溢出效应将得以充分分散，此时系统性风险将逐渐降低。平均偿付能力()对的影响显著为正，说明偿付能力的增强有助于降低系统性风险。

2影响因素的敏感性检验

由于样本数量限制，无法分行业进行单独回归，故进行敏感性检验，以展示上述因素在寿险和财险业的不同影响程度。具体做法是，逐一将上述因素提升至原来的2倍，并保持其他变量不变，以考察某一因素对财寿险系统性风险影响程度的差异。由于网络结构平均度是依据各公司间的再保险业务联系计算而得，无法通过参数调整来放大或缩小，故对的检验方法是维持财险各因素的原有水平，将寿险业其他三个变量调整至财险水平，并观察寿险系统性风险最终水平的变化幅度。

海水中悬浮物颗粒对光的选择性吸收是线性衰减系数不稳定的主要原因。在清澈的海域,除了蓝光的吸收和散射对光的衰减基本相等外,其他颜色的光衰减基本上是因为海水的吸收。在悬浮物比较多的海域,光的衰减则大部分来源于光的散射。而光在传播时产生的荧光散射和拉曼散射则包括了吸收和受激辐射两个基本过程。一般情况下,吸收作用造成的光量的衰减约占光源的40%,而其大部分原因是来源于光的散射作用。

(1)平均赔付率的影响。将平均赔付率分别调高为2倍，观察系统性风险的变化。图5中，虚线和实线分别为参数调整前和调整后的变化趋势曲线。当平均赔付率上升为2倍时，寿险和财险的都变为原来的12。这说明若平均赔付率上升，则只需较小的外部冲击就能导致同等数量的公司破产，此时的系统性风险水平更高。具体的变动比例说明，平均赔付率的变化对系统性风险的影响是同比例的，印证了承保风险与系统性风险之间存在正相关关系的推断。

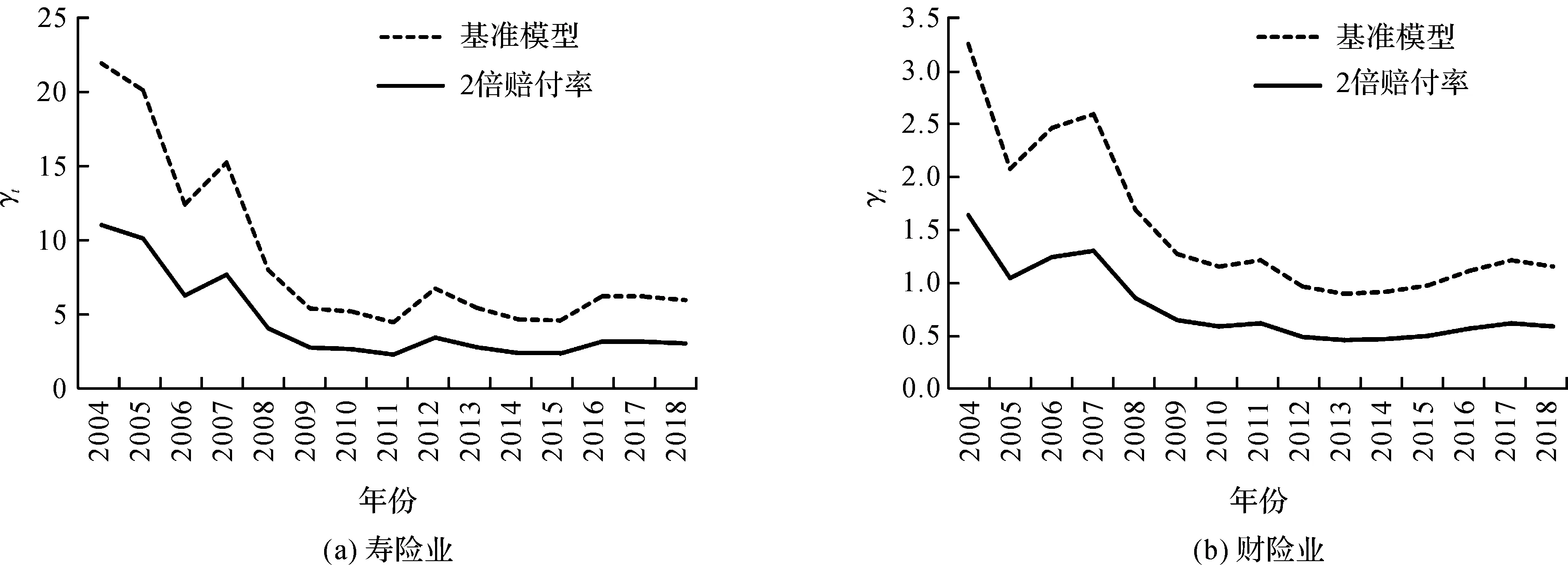
(2)平均再保险分出率的影响。根据图6，尽管平均再保险分出率上升为2倍时，同样导致了的下降，但下降幅度远未达到原来的12，说明再保险分出比例的上升对系统性风险的正向影响较弱。这是因为当分出比例上升时，对应分入公司的财务压力也将上升，但分入公司同样会办理分出业务，这在一定程度上分散了财务压力。因此，再保险分出率的提升对系统性风险的正向影响较弱。另外，寿险再保险分出率的变化仅给带来微弱影响，显著低于其在财险中的影响程度。

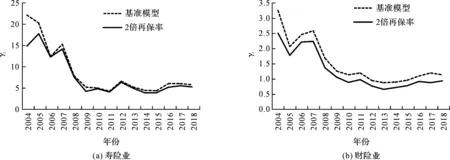
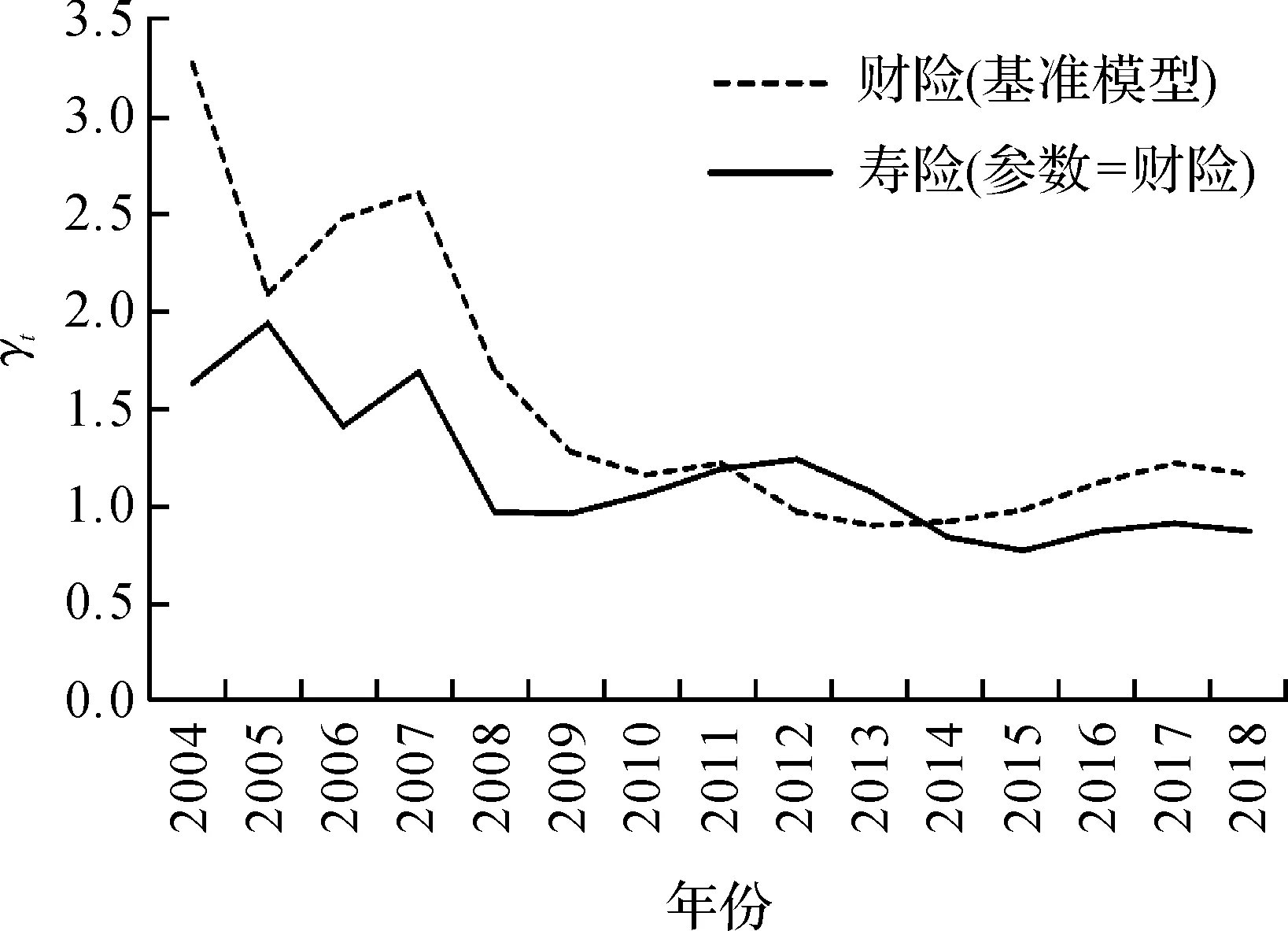
(3)网络结构平均度的影响。比较图7和图4发现，当将寿险其他参数均调整为与财险相同，仅保留网络结构的差异时，与财险的差距迅速缩小，甚至出现了交叉现象。由此可见，两行业间其他参数的差异是导致系统性风险存在差异的重要因素，且网络结构平均度对系统性风险的影响不是单纯的正向或负向关系，与表3中回归结果一致。网络结构平均度的增加在提升风险溢出效应的同时也增加了风险的分散程度，可能对系统性风险产生正向或负向的影响。

(4)平均偿付能力的影响。根据图8，当平均偿付能力增加为2倍时，寿险和财险的亦增加为2倍，即系统性风险下降为原来的12，说明平均偿付能力的变化对系统性风险的影响是同比例的。当偿付能力翻倍时，系统抵御非预期损失风险的能力随之翻倍，使得系统性风险同比例下降。

继2017年中国京菜走进巴塞罗那、走进哈萨克斯坦阿斯塔纳世博会参加巡展活动后，今年北京清真烹饪大师马志和先生代表北京烹饪协会接受邀请，赴联合国总部进行了京菜表演，收到了很好的效果，中国京菜得到了联合国官员的充分肯定和好评。在京菜美食节期间，还开展了老北京炸酱面比赛和中国京菜走进乡村等活动，振兴和发展中国京菜已成为北京餐饮企业增强市场竞争力的重要抓手。

(四)承保风险引致系统性风险差异的影响因素分析：基于公司层面

表4汇报了式(4)的回归结果。其中，模型1的被解释变量为公司是否因自身业务而破产，若无破产，=1；否则，=0，度量保险公司自身经营的稳定性。模型2的被解释变量为公司是否因被传染而破产，若无破产，=1；否则，=0。

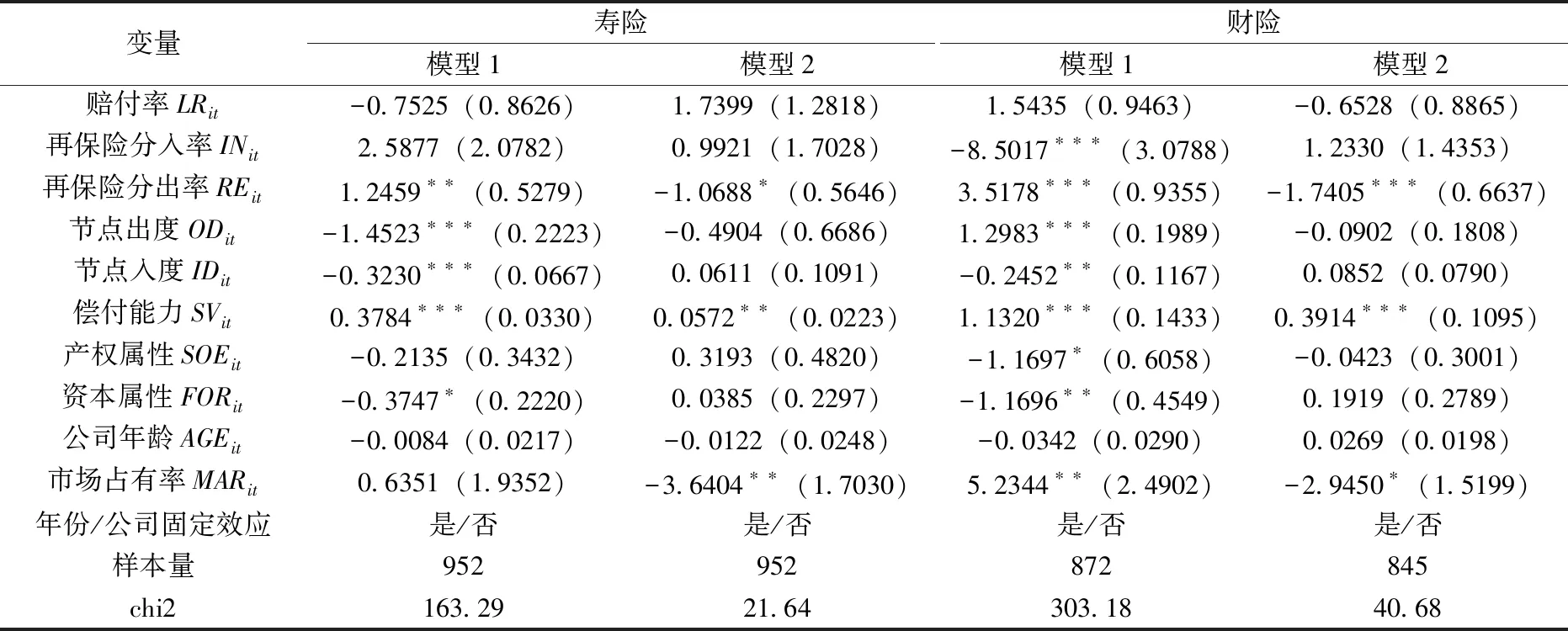
从模型1的结果来看，赔付率均不显著，说明同行业不同公司的赔付率接近，故赔付率的差异不是导致各公司稳定性差异的关键因素。再保险分入率在寿险公司中不显著，而在财险公司中显著为负，说明分入比例的增加不会影响寿险公司的稳定性，但会降低财险公司的稳定性。原因在于：寿险公司较少运用再保险，而财险公司则频繁使用，因此财险业分入比例的增加意味着接受了更多的承保风险，导致经营稳定性下降。再保险分出率在寿险和财险公司均显著为正，说明增加分出比例有利于提升公司经营稳定性，降低破产风险。结合表3可见，再保险分出对系统整体的稳定性具有负外部性，即承保业务的分出能降低自身的系统性风险，同时也使分入人的赔偿压力增大，促使行业系统性风险上升。节点出度在寿险和财险公司中分别显著为负和显著为正。结合理论分析可认为，出度的增加在寿险业中更多地体现为传染损失发生概率的增加，从而稳定性下降，而在财险业中则更多地表现为承保风险分散效应的增强，从而稳定性上升。节点入度在寿险和财险公司中均显著为负，说明分入业务交易对手的增加使寿险和财险公司的信息不对称风险增加，从而稳定性下降。偿付能力在两个行业均显著为正，说明偿付能力增加有助于增加经营稳定性。结合表3，保险公司增加偿付能力的行为对系统整体稳定性的影响具有正外部性，即当所有公司都更难破产时，承保风险的溢出效应将更难出现，系统性风险难以爆发。控制变量中，非国有和市场占有率较高的财险公司具有更高的稳定性，且外资公司稳定性均低于中资公司。

从模型2的结果来看，各公司因被传染而陷入破产的可能性主要受再保险分出率、偿付能力和市场占有率的影响。再保险分出率在寿险和财险公司中均显著为负，说明当其他公司违约时，分出率高的公司更易破产。结合模型1可见，再保险是一把“双刃剑”，既能帮助降低承保风险，又会增加“被牵连”的可能，使保险公司在风险传染时更脆弱。偿付能力均显著为正，再次说明偿付能力的增加有助于提升经营稳定性，即使遭受再保险违约，亦能更好地维持稳定经营。市场占有率均显著为负，说明市场占有率高的公司“受牵连”的可能性更大，这与本文假设有关。

对比模型1和2，模型2中显著的变量少于模型1，说明相比被传染至破产，保险公司自身破产的影响因素更多。此外，财险公司自身是否破产受更多因素影响。原因在于财险公司重视对承保风险的管理，而承保风险管理对寿险公司并非关键，导致寿险公司的承保风险管理较相似，显著因素少。但寿险和财险公司是否被传染而破产的影响因素及影响方向大体相似。这是因为两者的承保风险传染机制相同，所以影响因素的表现差异不大。

四、研究结论与政策建议

本文基于2004—2018年数据，建立了寿险和财险业承保风险网络，模拟和量化了承保风险导致的系统性风险，主要研究结论为：承保风险是导致系统性风险的来源；当前我国承保风险可控，尚未达到触发系统性风险的水平；寿险承保风险较低，但仍有引发系统性风险的潜质。行业层面上，平均赔付率和平均再保险分出率对系统性风险的影响显著为正，平均偿付能力的影响为负，而联系紧密程度的影响则为非线性；平均赔付率和平均偿付能力的影响敏感度较高，使系统性风险同比例变化；平均再保险分出率的影响敏感度较弱，使系统性风险的变化幅度较低。公司层面上，再保险分出率、节点出度、节点入度及偿付能力是影响保险公司自身稳定经营的关键因素，财险公司还受到再保险分入率的影响。再保险分出率和偿付能力是影响保险公司是否被传染的关键因素。

本文揭示出承保风险是导致保险业爆发系统性风险的根源。尽管保险业目前仍处在稳定状态，但控制巨灾风险仍是防范爆发系统性风险的关键所在，尤其应控制财险业的巨灾风险。可以采取下列措施：(1)深入探索最优再保险策略。公司层面上，控制再保险分出率和分入率，谨慎选择再保险交易对手，能有效降低自身破产和被传染的风险；行业层面上，再保分出会增加分入公司的财务压力，并加强各机构间的联系，从而使系统稳定性降低。因此，有必要探究寿险和财险业的最优再保险策略，以达到从公司自身和行业整体都能降低系统性风险的目的。(2)继续加强对保险公司偿付能力的监管。保险公司偿付能力的提升是防控保险业系统性风险的优良举措，不仅能够降低保险公司自身的破产风险，也能促使系统稳定性的增强。