基于弹性地基梁理论的跨活断层隧道围岩-衬砌体系破坏机制研究

马亚丽娜,舒 恒,崔庆龙,盛 谦 ,崔 臻

(1. 中交第二公路勘察设计研究院有限公司，湖北 武汉 430056；2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071；3. 中国科学院大学，北京 100049)

0 引言

随着我国经济建设持续向西部地区倾斜，我国西部高烈度地区的隧道工程建设也持续深入发展。西部地区的长大隧道工程，其巨大的工程规模、所处的复杂地质构造和恶劣的自然环境，为世界罕见，尤其是位于高烈度地震区域的隧道工程，穿越多条活动断裂带，对其安全运营存在严重威胁。一直以来，我国主要的地质勘察和隧道设计规范[1-2]均遵循避让活断层的原则，并要求满足一定避让距离。但受到选线限制，长大隧道工程将不可避免地穿越西部地区的复杂不良地质区域，接近或跨越活动断裂带与其影响区域。特殊隧道工程建设是关系到国家可持续发展的重大科技和战略课题，是我国重大基础设施发展的必然要求。因此，开展跨活断层隧道围岩-衬砌体系破坏响应和机制研究，显得迫切而有必要。

隧道工程的全部或部分结构处于围岩介质的约束之下，围岩与衬砌构成一个系统。在地质条件差或存在明显地质突变的活动断裂带附近，隧道结构易遭受破坏。伊朗学者KIANI[3]认为断层是一种永久性的地面位移，由于隧道纵向较长，易受到断层错动作用带来的破坏，学者针对跨正断层隧道开展了一系列物理模型试验，揭示隧道上覆土层的厚度、断层的角度对隧道受损范围和程度有一定影响。LIN[4]通过开展砂箱试验，研究强震诱发断层基岩逆冲作用下对隧道的影响，在砂箱试验中记录了土层内剪切带的发育、隧道在剪切带内位置和形状的变化等过程。随着计算水平的提高，数值模拟方法在工程设计中广泛应用。较室内试验而言，数值模拟可通过更短的时间和更低的成本进行参数研究，因此成为研究跨断层隧道围岩-衬砌响应的有效方法之一。BAZOAR[5]等采用有限元方法模拟了逆断层破裂从基岩向地表扩展的发展规律，讨论了上覆砂层中剪切带的位置和地下破裂痕迹的传播。ANASTASOPOULOS[6]等通过非线性有限元方法，模拟了准静态断层破裂在基岩上厚土层中的传播，以及破裂与沉管隧道的相互作用。徐前卫[7]等通过数值模拟手段，研究隧道工程穿越山区常见的较为软弱的Ⅳ级围岩时，隧道工程在施工中围岩的破坏特性和渐进性破损机制;总结出隧道的开挖会引起围岩应力的重分布，岩体应力在跨越断层两盘时呈现不连续且非线性的分布规律；但是，研究缺少了对岩体渐进性破坏条件下围岩-隧道相互作用，以及隧道内力和变形响应特征的分析。

依据弹性地基梁理论将工程结构进行简化处理，通过建立概化模型进行模拟，这种方法最早用于埋地管线错断问题的研究中。由于隧道与埋地管线均属于线形地下结构，二者具有相似的长大线性形状，并在断层错位作用下有相似的响应特征，基于弹性地基梁理论的管道错断模型分析方法，为长大隧道纵向变形及内力研究提供了思路。璩继立[8]将深埋盾构隧道等效为双面弹性地基梁，利用布辛奈斯克解求出隧道上部的附加应力，最后采用有限差分法求出隧道的纵向位移和内力，为深埋盾构隧道合理设计提供一定的依据。丁志军[9]基于双面弹性地基梁模型，借助有限元软件，分析了堆载条件下地铁隧道的纵向变形规律，揭示了基于双面弹性地基梁理论的有限元方法分析隧道纵向变形的可行性，以及埋深和堆载距离的增大都使得其对隧道纵向变形的影响逐渐减弱的规律。

综合以上研究成果发现，国内外目前针对断层错动条件下围岩渐进性破坏方面的研究已经取得了一些成果，但是对断层错动作用下跨断层隧道围岩-衬砌体系相互作用和破坏规律方面仍有待深入研究。并且，变形分析是隧道结构计算的一个重要部分，由于隧道的纵向变形特性相对横向更为脆弱，隧道纵向变形通常导致隧道向不利的方向发展[10-11]，目前的研究针对跨断层隧道纵向内力响应规律的分析较少。此外，目前研究鲜有将弹性地基梁理论引入跨断层隧道错断响应的研究中，基于弹性地基梁理论探索跨断层隧道围岩-衬砌破坏机制，此领域较为空白。

本文针对跨活断层隧道开展相应研究，主要基于以下2个方面：首先，本研究所基于的长大隧道的轴向长度远大于其截面尺寸，具有线形的特点；其次，数值分析方法可以在计算中考虑多个因素、模拟多种工况，并且，有限元数值分析方法可以解决隧道围岩-衬砌接触非线性，及大变形中几何非线性问题，是研究跨断层线状结构错断机理的有效手段。

因此，根据依托工程的工程地质条件，基于温克尔弹性地基梁理论，将隧道从几何、物理等角度简化为作用在地层上的弹性地基梁，采用法向弹簧和切向弹簧模拟地层与结构的相互作用；同时，利用有限元数值模拟手段，建立穿越活动断裂带隧道的围岩-衬砌体系二维数值模型，从而开展跨断层隧道围岩-衬砌体系破坏机制研究；最后，分析了断层倾角、断层宽度，岩体质量等级等多个因素对围岩-衬砌体系错断响应的影响，为跨断层隧道纵向设计提供一定的参考与理论支持。

1 温克尔地基梁理论

弹性地基梁为搁置在弹性地基上的梁式结构，梁上各点均与地基紧密接触。温克尔地基梁理论[12-15]为岩石力学与基础工程领域的常用计算方法，其基本假定为：将地基模拟为刚性支座上一系列的独立弹簧，在地基表面上，其中任何一处的沉降量都将与该处在单位面积中所承受的压力大小成正比。将此理论引入本研究，对活动断层错动条件下隧道衬砌的模拟做出如下假定：

a.假定隧道衬砌在断层错动作用下的变形是平面内二维变形，且将隧道简化为实截面梁。

b.假定断层错动作用下隧道与围岩之间的相互作用以衬砌两侧地基弹簧的形式体现。

c.忽略自重应力与构造应力等初始应力。

d.忽略断层错动的时间动力效应。

此外，计算都要达到2个最为基本的求解要求，即地基与地基梁之间的静力平衡要求，以及变形协调的要求。基于此，在断层两侧围岩错动条件下，地基弹簧与岩土体之间发生的相互作用，表现为隧道结构的梁单元微元体内部产生的轴力、剪力、弯矩等内力响应。隧道在断层错动作用下的变形图和梁单元微元体结构如图1所示。

图1 断层错动作用下隧道纵向变形和梁单元微元体结构

2 计算模型的搭建与计算方案

以跨越多条活动断裂的香炉山隧道工程为研究对象。工程区域构造运动剧烈，发育了众多类型、活动性和规模各异的活断层，地震活动性较强，区域内潜在震源区和主要断层分布如图2所示。隧道沿线主要跨越断层总长约588 km，本研究以规模最大、对隧道威胁最强烈的F10-1断层为例进行分析，该断层表现出多期活动的复合性质，对隧道工程的安全运营存在严重威胁[16]。

(1)小江地震活动带; (2)通海-石屏地震活动带; (3)中甸-丽江-大理地震活动带; (4)腾冲-龙陵地震活动带; (5)耿马-澜沧地震活动带; (6)马边-大关地震活动带; (7)思茅-普洱地震活动带; (8)南华-楚雄地震活动带

2.1 计算模型及边界条件

根据弹性地基梁理论，将隧道简化为二维平面上的一条梁，隧道与围岩的相互作用采用地基梁两侧弹性接触单元进行模拟，断层沿主断带发生剪切。采用有限元软件PHASE2建立二维计算模型如图3。根据依托工程调研参数，选取模型中断层倾角90°，断层宽度330 m，其中破碎带部分的宽度为150 m；衬砌为弹性，断面为圆环状，采用C30混凝土，厚度选取为0.5 m。计算模型中，断层左侧部分(上盘)边界条件采用固定约束，右侧部分(下盘)中，右端采用水平向约束，下盘整体赋予竖向向上的位移，通过上下两盘的相互运动以模拟正断层的错动。

图3 模型计算模型

通过试算，得到衬砌结构内力沿隧道轴线方向的分布规律，总结出临近数值模型边界时，衬砌纵向弯矩已趋近于0，表明当前采用的剪切错动加载方式与模型范围是合理的，可应用于后续研究。

2.2 材料参数选取

针对依托工程，根据已有室内物理试验成果[17]进行拟合，从而确定破碎带内围岩-衬砌接触参数，法向刚度选取为2 000 MPa/m，切向刚度选取为3 000 MPa/m，在模型中体现为地基弹簧的变形参数；良好围岩区域内围岩-衬砌接触参数选取为：法向刚度100 000 MPa/m，切向刚度10 000 MPa/m。此外，围岩模拟材料与衬砌结构的计算参数依据现行的规范取值，材料物理力学参数取值如表1所示。

表1 材料物理力学参数指标Table 1 Physical and mechanical parameters of materials密度 /(kg·m-3)杨氏模量/GPa接触刚度/(MPa·m-1)泊松比粘聚力/MPa内摩擦角/(°)围岩2 60016.0100 000(Kn) 10 000(Ks) 0.31.250破碎带2 2004.0 2 000(Kn) 3 000(Ks) 0.350.530隧道衬砌2 50030.0—0.2——

2.3 计算方案

开展断层错动条件下，断层破碎带地质条件对跨断层隧道围岩-衬砌体系错断响应影响分析，初始计算方案为：断层倾角为90°，断层破碎带宽度为150 m，断层破碎带弹性模量为4.0 GPa，断层破碎带内隧道围岩-衬砌法向刚度为2 000 MPa/m，切向刚度为3 000 MPa/m。根据断层位移设防量，开展断层错动量为1.2 m时隧道围岩-衬砌位移变化规律和衬砌内力响应特征的研究。

3 跨断层隧道围岩-衬砌体系错断响应分析

在本研究中，以目标区域在基本烈度条件下断层错动量约为1.2 m作为输入条件展开计算。研究正断层错动作用下跨断层隧道围岩-衬砌体系错断响应规律，计算模型如图4所示。

图4 基本烈度下计算模型图

3.1 围岩-衬砌体系位移响应

围岩位移云图如图5所示，断层两盘错动影响的范围主要是在地质条件较差的断层破碎带内，且集中于断层错动面两侧各30 m的范围内，围岩位移在断层错动面处变化连续。

图5 断层围岩位移云图

图6展示了隧道衬砌位移沿隧道纵向分布曲线。从图中可以看出，隧道衬砌在断层破碎带内急剧变形，且变化率基本一致；断层上盘内，衬砌位移量较小，左端接近静止状态，而在断层下盘内，由于受到围岩约束作用，衬砌位移量较大，右端位移量与断层错动的最终状态接近一致。

图6 衬砌位移沿隧道纵向分布曲线

3.2 衬砌结构内力响应

3.2.1弯矩

图7展示了断层错动量1.2 m时衬砌弯矩沿隧道纵向的分布曲线。从图8中可以看出，断层破碎带内衬砌弯矩发生明显变化，且变化率一致；此外，衬砌弯矩在断层上下两盘内受到的弯矩作用方向相反；在远离断层破碎带处，弯矩值趋于稳定且量值较小；在断层破碎带与围岩交界处产生弯矩极值，为重点设防部位。

图7 衬砌弯矩沿隧道纵向分布曲线

3.2.2剪力

图8展示了断层错动量1.2 m时衬砌剪力沿隧道纵向的分布曲线。由图8可知，在断层破碎带、围岩交界处和中心剪切带附近，衬砌剪力变化率较大；在断层中心剪切带处，衬砌剪力达到峰值；而在远离断层破碎带处，剪力量值稳定且较小。因此，在断层破碎带、围岩交界处和中心剪切带附近，隧道衬砌易遭受剪切破坏，此部位应重点设防。

图8 衬砌剪力沿隧道纵向分布曲线

3.2.3轴力

图9展示了断层错动量1.2 m时衬砌轴力沿隧道纵向的分布曲线。以衬砌轴向受拉为正，轴向受压为负。由图9可见，断层两盘内衬砌轴力以中心剪切带对称分布；衬砌在断层破碎带以外的区域主要呈现受拉状态，而在断层破碎带内主要呈现受压状态。此外，在断层破碎带内的中心剪切带附近，衬砌轴力变化率较大，衬砌轴力在中心剪切带两侧达到峰值，此处应重点设防。

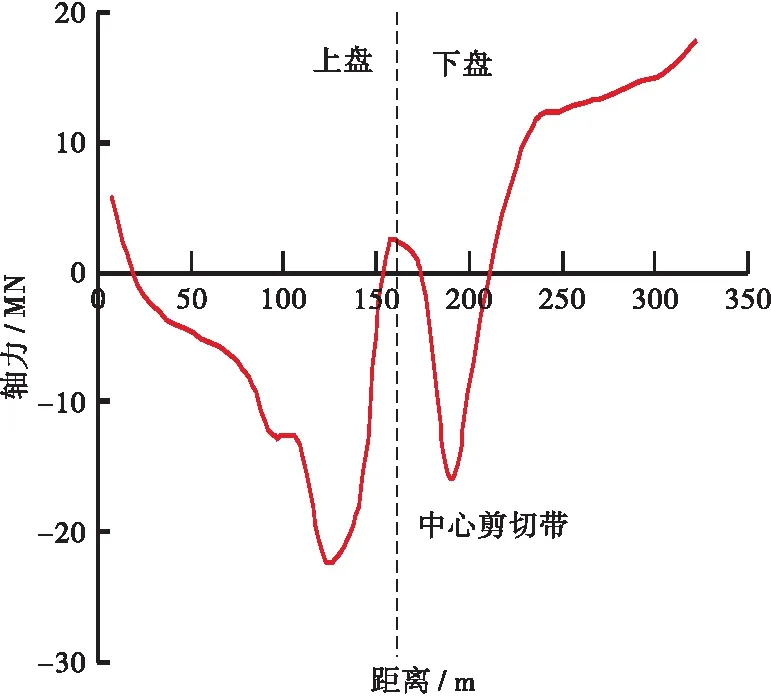
图9 衬砌轴力沿隧道纵向分布曲线

4 断层破碎带地质条件影响分析

针对断层破碎带地质条件，本文探讨了断层破碎带倾角、断层破碎带宽度，以及断层破碎带岩体力学参数对跨断层隧道错断响应的影响。

4.1 断层破碎带倾角的影响

本节讨论了断层倾角对围岩-衬砌错断响应的影响规律。计算工况如表2所示，数值计算模型如图10所示。

(a) 断层倾角70°

表2 不同断层倾角下计算工况Table 2 Calculation cases under different fault dip angles断层破碎带倾角/(°)断层破碎带宽度/m断层破碎带弹性模量/GPa接触刚度/(MPa·m-1)70 1504.02 000(Kn)3 000(Ks)801504.02 000(Kn)3 000(Ks)901504.02 000(Kn)3 000(Ks)

4.1.1围岩-衬砌位移分析

图11(a)、 图11(b)、 图11(c)分别展示了70°、80°和90°断层倾角条件下断层围岩位移云图。不同断层倾角下，断层围岩两端最终位移量值大小一致；但在断层破碎带内，断层倾角越小，断层错动作用影响范围明显增大。图12展示了不同断层倾角下衬砌位移沿隧道纵向的分布曲线。断层倾角变化对衬砌位移曲线差异性影响较小，不同断层倾角下的衬砌位移沿隧道纵向的分布规律基本一致，仅在断层破碎带内有些许差别，当断层倾角为70°时，衬砌位移曲线变化缓慢，随倾角增加而增大，断层倾角80°和90°条件下衬砌位移曲线几乎一致。

(a) 断层倾角70°

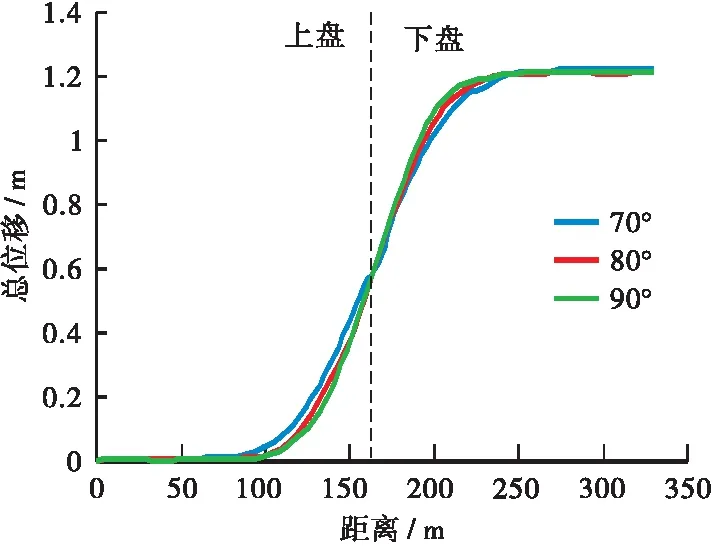
图12 不同断层倾角下衬砌位移沿隧道纵向分布曲线

因此，断层倾角变化对衬砌位移曲线差异性影响较小；断层倾角较小时，断层错动作用影响范围较大，需在较大范围内采取有效措施以保证隧道抗错断性能。

4.1.2衬砌内力纵向分布特征致。断层破碎带内，断层倾角大小对衬砌内力的影响体现在范围和峰值2方面。随着断层倾角增大，衬砌弯矩和剪力变化范围减小，但峰值呈现增大状态，断层破碎带内衬砌受压现象显著减小，轴力峰值明显降低。当断层倾角从70°变化至90°时，弯矩和剪力变化范围明显减小，而弯矩峰值从1 630.5 MN·m增大至2 535.5 MN·m，变化幅度约55.5%，剪力峰值从64 MN增大至140 MN，变化幅度为118.8%，这是由于当断层倾角较大时，断层错动对衬砌剪力影响程度较大，剪切作用更为直接地作用于隧道衬砌，将作用于衬砌上的拉应力转化为剪应力，导致衬砌剪力增大；上述倾角的变化使轴力峰值从234 MN减小到了22 MN，其原因是衬砌从发生拉剪变形转换为剪切变形。另外，随着断层倾角增大，断层中心剪切带处衬砌轴力变化率明显降低，是由于衬砌受到的拉伸变形不协调作用减小，衬砌沿隧道纵向的拉伸作用被减轻。

图13展示了不同断层倾角下衬砌内力沿隧道纵向的分布曲线。从图13中可见，衬砌内力沿隧道纵向的分布趋势在不同断层倾角条件下基本一

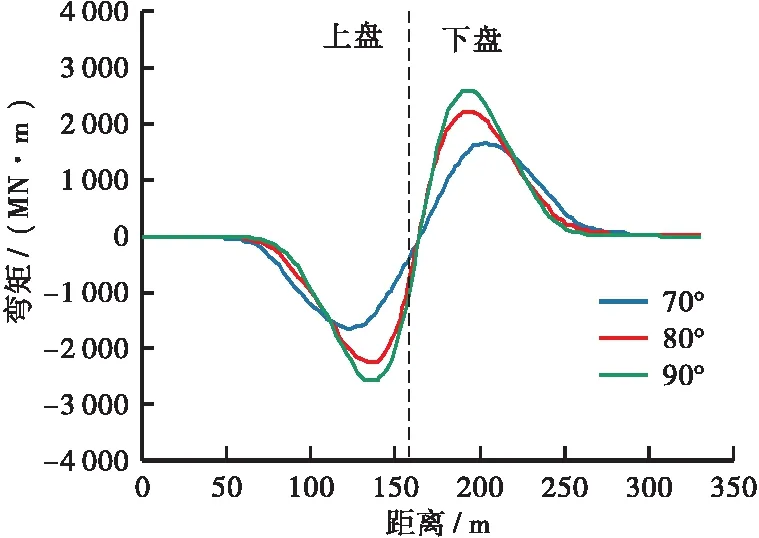
(a) 弯矩

因此，隧道应以较大角度跨越断层，有利于提高隧道的抗错断性能。

4.2 断层破碎带宽度的影响

本节讨论破碎带宽度对围岩-衬砌错断响应的影响，计算工况如表3所示，数值计算模型如图14所示。

表3 不同破碎带宽度下计算工况Table 3 Calculation cases under different fault width断层破碎带倾角/(°) 断层破碎带宽度/m断层破碎带弹性模量/GPa接触刚度/(MPa·m-1)901004.02 000(Kn)3 000(Ks)901504.02 000(Kn)3 000(Ks)902004.02 000(Kn)3 000(Ks)

(a) 断层宽度100 m

4.2.1围岩-衬砌位移分析

图15(a)、 图15(b)、 图15(c)分别展示了100、150和200 m的断层破碎带宽度下断层围岩位移云图。不同断层宽度下，断层围岩两端最终位移量值大小一致；但在断层破碎带内，断层破碎带宽度越大，断层错动作用影响范围明显增大。图16展示了不同断层破碎带宽度下衬砌位移沿隧道纵向的分布曲线。从图中可以看出，断层宽度变化对衬砌位移曲线差异性影响很小，不同断层宽度下的衬砌位移沿隧道纵向的分布规律基本一致。

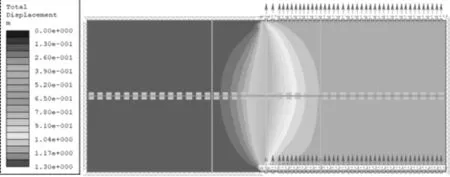
(a) 断层宽度100 m

图16 不同断层宽度下衬砌位移沿隧道纵向分布曲线

4.2.2衬砌内力纵向分布特征

图17展示了不同断层破碎带宽度下衬砌内力沿隧道纵向的分布曲线。由图17可见，衬砌内力沿隧道纵向的分布趋势在不同断层宽度条件下基本一致。整体来看，破碎带宽度不同对衬弯矩的影响较小，但对剪力和轴力具有一定影响。断层破碎带宽度对剪力的影响主要体现在变化范围和峰值这2个方面，随着断层宽度增大，剪力变化范围增大，但剪力峰值明显减小；当断层宽度从100 m变化至200 m时，剪力影响范围增大，剪力峰值减小幅度为23.5%，这是因为衬砌弯曲变形的范围随断层宽度的增大而增大，应力集中现象被削弱。对于轴力而言，当断层宽度较大时，衬砌在断层破碎带内主要呈现受压状态，轴力峰值和变化率降低。此外，衬砌轴力伴随断层宽度的增大而逐渐减小，峰值随之降低，变化率减小，这是因为断层宽度增大后减轻了衬砌在破碎带内的不协调拉伸变形现象，正摩擦力减小。

(a) 弯矩

因此，若隧道选线不可避免地跨越活动断裂带，较大的断层宽度对隧道衬砌受力状态更有利。

4.3 断层破碎带岩体力学参数的影响

本小节研究破碎带岩体力学参数对围岩-衬砌位移特性和衬砌内力响应的影响进行讨论。其中，计算工况如表4所示，数值计算模型如图18所示。

表4 不同岩体力学参数下计算工况Table 4 Calculation cases under different mechanical pa-rameters of fault rock mass断层破碎带倾角/(°)断层破碎带宽度/m断层破碎带弹性模量/GPa接触刚度/(MPa·m-1)901501.0 500(Kn) 750(Ks)901502.01 000(Kn) 1 500(Ks)901504.02 000(Kn)3 000(Ks)

(a) 弹性模量1 GPa、法向刚度500 MPa/m、切向刚度750 MPa/m

4.3.1围岩-衬砌位移分析

图19 (a)、 图19 (b)、 图19 (c)分别展示了不同断层破碎带岩体力学参数下断层围岩位移云图。在同样的断层错动量下，围岩位移云图并无明显差异，说明断层破碎带岩体质量对围岩位移作用范围影响较小。图20展示衬砌位移沿隧道纵向的分布曲线。在断层岩体质量不同的情况下，衬砌位移曲线在变形趋势上基本一致，仅仅破碎带内有些许差别。岩体强度越小，衬砌位移曲线变化缓慢，原因是断层破碎带岩体质量等级越低，强度越小，对隧道的约束性能越强弱，越能够吸收断层错动对隧道衬砌变形产生的能量，位移变化率越小。

(a) 弹性模量1 GPa、法向刚度500 MPa/m、切向刚度750 MPa/m

图20 不同断层岩体力学参数下衬砌位移沿隧道纵向分布曲线

因此，断层带岩体质量等级越高，强度越大，断层破碎带对衬砌结构约束性越强，隧道洞受到断层错动作用越显著。

4.3.2衬砌内力纵向分布特征

图21 (a)、 图21 (b)、 图21 (c)展示了不同断层岩体力学参数下衬砌弯矩沿隧道纵向分布曲线。断层破碎带内，不同断层岩体力学参数下衬砌内力沿纵向分布曲线具有明显差异。随着岩体力学参数减小，当岩体模量从4 GPa降低至1 GPa时，弯矩峰值减小幅度约为38%，剪力峰值减小幅度为53.6%。这是由于较弱断层破碎带岩体质量，对隧道约束较弱，能够吸收断层错动带来能量并降低弯矩和剪力分布曲线陡峭程度，则较弱断层岩体质量更有利于保护隧道衬砌遭受剪切破坏。对于轴力指标，随着断层岩体力学参数减小，衬砌轴力峰值减小，断层剪切带处衬砌轴力变化率明显减小。

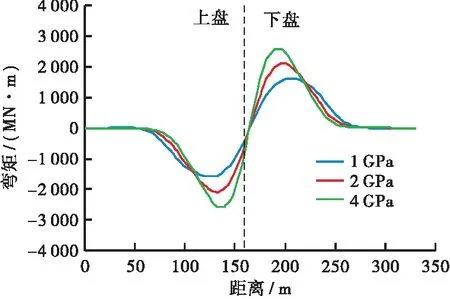
(a) 弯矩

因此，当隧道不可避免地跨越活动断层时，较弱的破碎带岩体质量可以有效减轻断层错动对衬砌结构带来的破坏。

5 结论

本研究基于温克尔弹性地基梁理论，利用PHASE2数值模拟软件，建立跨断层隧道围岩-衬砌数值模型，探讨不同断层因素对跨断层隧道围岩-衬砌体系响应特征的影响，主要结论如下：

a.断层两盘错动影响的范围主要是在地质条件较差的断层破碎带内，且集中于断层错动面两侧各30 m的范围内；在中心剪切带处，围岩上下两盘位移连续。

b.衬砌发生急剧变形的范围主要集中在断层破碎带内；在断层两盘交界处衬砌位移连续，衬砌在断层上下盘内受到相反的弯矩作用，且均匀变形。

c.在断层破碎带内,隧道以受压为主，而在远离断层带处主要呈现受拉状态；衬砌在断层破碎带、围岩交界处和中心剪切带附近遭受剪切破坏，此处应重点设防。

d.不同的断层倾角、破碎带宽度、岩体质量等级均对围岩-衬砌体系错断响应规律产生一定影响。跨断层隧道穿越活断层的最佳角度为正交；断层宽度大小影响断层错动作用的影响范围和衬砌内力峰值，当断层宽度从100 m变化至200 m时，剪力响应范围增大，剪力峰值减小幅度为23.5%，弯矩和轴力峰值降低，衬砌错断响应在更大的范围内分散分布，避免了应力集中现象；断层错动量一定条件下，当岩体模量从4 GPa降低至1 GPa时，弯矩峰值减小幅度约为38%，剪力峰值减小幅度为53.6%，因此断层破碎带岩体质量等级越高，隧道受到断层错动作用越显著。

e.本文研究结果可为跨活动断裂隧道的围岩-衬砌错断响应与机理研究提供一定参考，但鉴于本文研究的局限，如为了模型简化考虑，错断模型较为概化，边界条件设置较为简单，这些问题有待在以后的工作中作进一步的研究与讨论。